地下隧道支护结构的受力分析

鹿宁，邱敏，陶磊

（1.中国水电顾问集团西北勘测设计研究院，陕西西安 710065；2.西安理工大学水利水电学院，陕西 西安 710048）

地下工程通常包括在地面以下开挖各种隧道与洞室。随着科学技术的进步，铁路、公路、水电以及城市地铁等诸多领域的地下工程得到了进一步发展。地下结构在工作环境、力学作用机理方面与地面工程存在着明显的差异，因此利用地面工程的理论和方法去解决地下工程的各类问题时，往往不能正确地解释地下工程出现的诸多现象，有必要寻求解决地下工程问题的新理论、新方法[1-2]。

地下工程支护结构理论的一个重要问题是确定作用在地下结构上的荷载。支护结构理论的发展经历了3个阶段[3-4]：1）古典的压力理论阶段。如海姆、朗肯和金尼克理论等，认为作用在支护结构上的压力是其上覆岩层的重量γH（γ是岩层容重；H是埋深）。不同学者，对地层水平压力的侧压系数有不同的取法。2）散体压力理论。这类理论认为坍落拱的高度与地下工程跨度和围岩性质有关。太沙基认为坍落拱为矩形，普罗托季亚科诺夫认为是抛物线形。3）现代支护理论。以岩石力学理论为基础、考虑支护与围岩共同作用的现代支护理论。史密德和温德耳斯按连续介质力学方法计算圆形衬砌的弹性解；徐干成、郑颖人等利用弹性力学获得了在非均压地层压力作用下围岩与支护共同作用的线弹性解；塔罗勃和卡斯特奈得出了圆形洞室的弹塑性解。

围岩是隧道支护结构体系的一部分，同时围岩又产生荷载，通常视围岩为连续介质来传递荷载和提供支撑作用[1]。进行隧洞衬砌结构设计时，传统的方法是将围岩压力进行简化，考虑围岩压力以几种形式作用于衬砌结构上，从衬砌结构横断面来看，划分为垂直围岩压力、侧向围岩压力和底部围岩压力3种形式，如图1所示。隧道支护结构的内力计算时，常使用传统的结构力学法，将拱圈和侧墙分开计算，考虑两者之间的相互影响，计算过程十分繁琐，且数值运算量大，从而造成结构设计效率低下。本文基于弹性地基理论和有限元法，采用ANSYS程序，建立了隧道衬砌结构的有限元模型，利用壳单元SHELL63中的Winkler弹性地基系数[5]来模拟底板和侧墙的围岩压力，根据国内外研究围岩压力的3种方法确定拱圈的围岩压力。通过有限元分析，得到支护结构的内力和变形，并对支护结构的4个典型截面进行了强度复核。

图1 围岩压力计算简图Fig.1 Calculation diagram of the surrounding rock pressure

1 地下隧道结构有限法

1.1 计算原理

支护结构的计算采用局部变形地基梁法，把拱圈和侧墙分开来计算，将衬砌看作是支承在2个竖直的弹性地基上的拱圈。拱圈按弹性固定在墙顶上的无铰拱计算，侧墙按照竖放的弹性地基梁计算，在各自的计算中考虑拱圈和侧墙的相互影响，拱脚截面的转角和水平位移须由侧墙墙顶转角和水平位移确定。分析时，将围岩压力简化为垂直底部围岩压力、侧向底部围岩压力以及底部围岩压力，围岩压力的计算简图如图1所示。侧墙和底板应用局部变形理论来考虑到围岩对支护结构的作用，即假定单位面积上的围岩压力与该点法向变形成正比。利用ANSYS中弹性壳单元SHELL63单元的弹性地基系数（EFS）来模拟围岩对侧墙和底板支护结构的作用，根据文献[6]中垫层系数表选取。在不使用弹簧单元的情况下，相当于壳单元表面施加一系列法向独立的弹簧，从而简化了有限元模型。ANSYS的壳单元可以很方便地输出单元的内力如单位宽度的轴力、弯矩，如式（1）和式（2）所示。

式中：Tx、Mx分别为壳单元单位宽度的轴力和弯矩；t为单元的厚度；σx为正应力。

对于线弹性材料，式（1）和式（2）可简化为

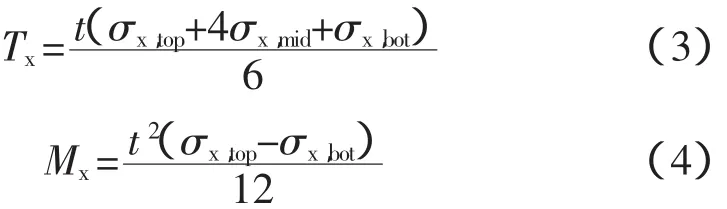
式中，σx，top、σx，mid、σx，bot分别为单元顶面、中面和底面的正应力。

1.2 计算简图

隧道支护结构是一种由拱圈和侧墙作为其承重构件的地下结构[6-7]。由于侧墙和拱圈整体浇筑，隧道结构具有整体性和受力性能好的特点。此外，结构与围岩紧密相贴，所以能有效阻止围岩的继续风化和塌落，毛洞开挖量小。隧道结构是一个长廊形的空间结构，由于断面形状、荷载大小分布与支承情况沿纵向不变，且沿纵向长度远大于跨度的两倍，因此一般可看作平面问题处理，将纵向取单位宽度进行计算[8-9]。

隧道支护结构有限元分析的计算简图如图2所示。

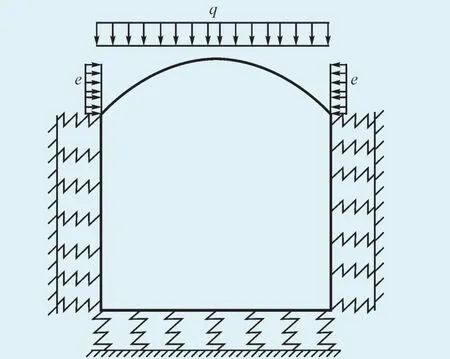
图2 有限元分析的计算简图Fig.2 Calculation diagram of the finite element analysis

2 工程实例

2.1 设计基本资料

某实际工程隧道剖面图如图3所示，侧墙厚度为650 mm，底板的厚度为600 mm，对隧洞开挖后的围岩进行了系统的分类，得出了该开挖段围岩类别为Ⅳ类。因隧洞围岩的稳定性较差，施工时针对不同区段采用了不同钢支护形式。

图3 隧道剖面图Fig.3 Tunnel profile

2.2 有限元分析

2.2.1 有限元模型

图4给出了隧道结构的有限元模型，采用弹性壳单元SHELL63来模拟侧墙、底板和拱圈。其中侧墙和底板的弹性地基系数根据文献[3]，按硬土、岩石取200×106N/m3，隧道衬砌结构的自重由程序自动计入。以隧道左下角为坐标原点，沿底板方向为x轴，以进入隧道的方向为y轴，竖向为z向。约束隧道的y向位移。

图4 隧道有限元模型Fig.4 Tunnel finite element model

2.2.2 围岩压力

围岩压力的确定有3种方法，即：综合经验公式法、直接荷载确定法和普氏地压理论。

1）综合经验公式法。

围岩垂直均布压力：

式中：N0为Ⅳ类围岩，取1.4 ～1.6。本文取N0=1.5；KL为取lm/6，本文取0.95，lm为毛洞跨度；γ为围岩容重取26 kN/m3。垂直均布压力为q=370 kPa。

围岩水平均布压力：

本文取e=148.20 kPa。

2）直接荷载确定法。

围岩垂直均布压力：

式中，取i=0.1，当lm=5 ～15 m，

因此ω=1.068，q=498.42 kPa。

围岩水平均布压力：

本文取e=83.07 kPa。

3）普氏地压理论。

作用在衬砌上的垂直均布压力为

作用在衬砌上的水平围岩压力为

取φ=30°，得q=90 kPa，e=30 kPa。

3种围岩压力确定方法得到的荷载列于表1中，由表1可见，3种方法得到的荷载相差较大，其中普氏地压理论的荷载最小。

表1 Ⅳ类的围岩压力3种计算方法荷载对比Tab.1 Comparisons of the surrounding pressure of classⅣrock by three methods

2.2.3 有限元分析结果

利用上述3种方法计算出来的荷载，施加到有限元模型上，进行静力计算。内力及位移计算结果如表2所示。

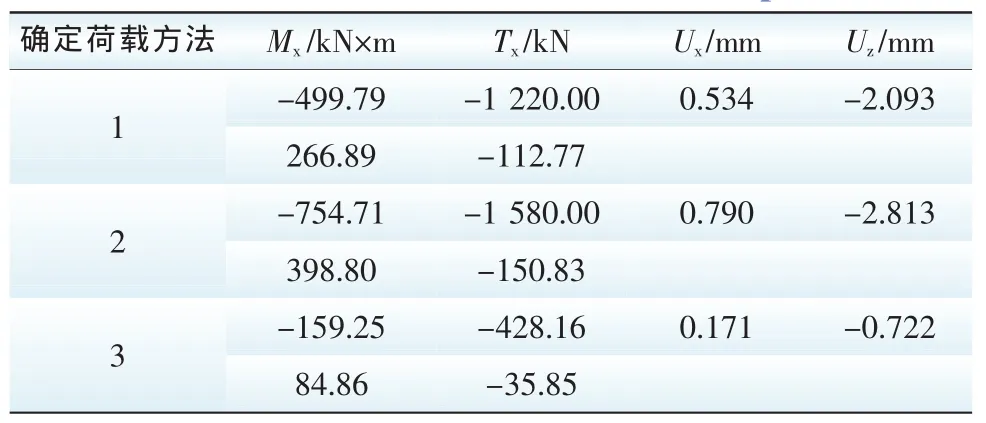
表2 内力及位移计算结果Tab.2 Results of the internal force and displacements

对隧道支护结构洞顶、侧墙顶部拱脚、侧墙中部和底板中部4个截面进行强度复核。强度复核先按不考虑钢支护作用计算，再按考虑钢支护作用计算，分析钢支护对强度的提高。4个截面的配筋和钢支护图如图5所示。

图5 围岩衬砌典型截面处的配筋图和型钢位置图Fig.5 Reinforcement figure and profile steel draw ing at the location of a typical surrounding rock lining

对于图5所示的各截面，根据3种荷载确定方法相应的内力结果，按偏心受压构件进行强度复核。复核时采用内力的设计值。混凝土按C25、支护型钢按Q235、钢筋按HRB335的力学参数进行强度复核。

对于截面尺寸和材料强度确定的偏心受压构件，达到承载力极限状态时，截面承受的极限轴力Nu和极限弯矩Mu不是独立的，而是相关的。以M为横轴，以N为纵轴，可以绘出Nu-Mu相关曲线。偏心受压分为大偏心受压和小偏心受压。小偏心受压时，随着轴力的增加，构件的抗弯能力减少；而大偏心受压破坏时，轴力增大后，构件的抗弯能力反而增加，两种破坏形式的验算方法是不同的。由于不同荷载确定方法相应的截面弯矩、轴力相差很大，因此计算偏心距也很大，给定偏心距，弯矩轴力将不再独立，所以本文仅按轴力复核时，强度满足下列要求：

式中：N为轴力设计值；Nu为极限轴力。

表3给出了Ⅳ类围岩段衬砌典型截面处由不同围岩荷载方法计算的截面内力。

表3 Ⅳ类围岩段衬砌典型截面处的弯矩和轴力Tab.3 M oment M and axial force N at the location of typical surrounding rock lining for classⅣ

表4给出了Ⅳ类围岩衬砌的4个截面按偏心受压的强度复核结果，由于型钢截面的高度远小于衬砌厚度，所以在计算中按钢筋加以处理，强度复核分不考虑钢支护和考虑钢支护两种，以期探讨钢支护对于衬砌的结构的提高作用。

为了便于复核评价，定义安全裕度如下：

考虑钢支护作用后，极限承载力提高率如下：

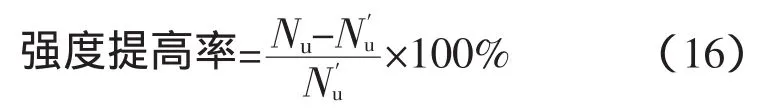
式中：Nu为考虑钢支护的极限轴力为不考虑钢支护的极限轴力。

根据有限元计算结果，4个典型截面处的弯矩和轴力列于表3中。强度复核时，应采用内力的设计值，故需将表中的标准值乘以1.2的分项系数。

由表4可知，对于Ⅳ类围岩衬砌结构，在不考虑钢支护作用的情况下，洞顶按综合经验法确定的荷载下强度稍不满足，其余各截面按各种方法确定的荷载作用下强度均满足要求。考虑钢支护作用情况下，各截面的强度均有所提高，洞顶强度提高率为13.5% ～27.6%，拱脚的提高率为75.8% ～85.9%，侧墙中部的提高率为18.7% ～23.9%。

表4 Ⅳ类围岩衬砌强度复核结果Tab.4 The reviewed result of the lining strength of the surrounding rock of classⅣ

3 结论

本文介绍了地下工程支护结构的相关理论，同时比较了3种隧道衬砌结构的荷载确定方法。对Ⅳ类围岩段衬砌结构按不同的理论确定了围岩压力，基于弹性地基理论和有限元法，应用ANSYS建立了某隧道支护结构的有限元模型，通过有限元分析，得到了结构的位移和内力，并对该支护结构进行了强度复核。

[1] 曾艳华，王英学，王明年.地下结构ANSYS有限元分析[M].成都：西南交通大学出版社，2008.

[2] 徐干成，白洪才，郑颖人，等.地下工程支护结构[M].北京：中国水利水电出版社，2002.

[3] 王后裕，陈上明，言志信.地下工程动态设计原理[M].北京：化学工业出版社出版社，2008.

[4] 李志业，曾艳华.地下结构设计原理与方法[M].成都：西南交通大学出版社，2003.

[5] 殷宗泽.土工原理与计算[M].北京：中国水利水电出版社，1996.

[6] 肖明，叶超，傅志浩.地下隧洞开挖和支护的三维数值分析计算[J].岩土力学，2007，28（12）:2501-2505.XIAO Ming，YE Chao，FU Zhihao.Three-dimensional numerical simulation and analysis of excavation and support in underground tunnel[J].Rock and Soil Mechanics，2007，28（12）:2501-2505（in Chinese）.

[7] HIROO KUMASAKA.Numerical computation of support characteristic curves for use in tunnel support design and their application to the characteristic curve method[J].International Journal of the JCRM.2007，3（1）:1-6.

[8] 张红，郑颖人，杨臻.黄土隧洞支护结构设计方法探讨[J].岩土力学，2009，30（12）:473-478.ZHANG Hong，ZHENG Yingren，YANG Zhen.Exploration of design methods of support structure in loess tunnel[J].Rock and Soil Mechanics，2009，30（12）:473-478（in Chinese）.

[9] 杨臻，郑颖人，张红.岩质隧洞支护结构设计计算方法探索[J].岩土力学，2009，30（8）:148-154.YANG Zhen，ZHENG Yingren，ZHANG Hong.Explorating computational method of designing the supporting structure of rock tunnel[J].Rock and Soil Mechanics，2009，30（8）:148-154（in Chinese）.