基于多位置NWP的超短期风速预测研究
任亮,赵兴勇
(山西大学电力工程系,山西太原 030013)
风能作为一种可再生、洁净的能源,近年来在全世界范围内得到了突飞猛进的发展。由于受地形条件和气候环境的影响,风能具有较大的间歇性、波动性、低能量密度和不可控性等特点。风电场出力不稳,给电网调度、调峰、安全等带来一系列问题。为了提高风电场发电效率、配合电网公司调度需求,满足电网并网技术标准发展要求,需要对风电场的发电功率进行准确的预测。这样可以有效地减少由于旋转备用容量增加而导致的风力发电系统成本的增加[1],并且为电力系统的运行和调度提供可靠的依据。
电网调度部门对风电功率预测的基本要求有2个:一是短期预测,即当天预测次日00:00时起72 h的风电场输出功率,时间分辨率为15 min,目的是便于电网合理调度,保证供电质量;另一个是超短期预测,即实现提前量为0 ~4 h的滚动预测,目的是对风电机组进行控制,便于电力系统实时调度。根据风电机组的特性曲线可由风速计算出功率,因此功率预测问题可转化为风速预测问题。常用的预测方法有时间序列法[2-3]、卡尔曼滤波法[4-5]、神经网络法[6-8]、灰色预测法[9-10],以及上述方法的不同组合[11-12]。
目前风电场功率预报系统中包括了数值天气预报产品,各预测模型的准确度很大程度上依赖于数值天气预报的精度。由于多位置NWP信息输入神经网络会大大增加网络的计算量和问题的复杂性,本文提出了基于主成分分析结合神经网络的超短期风速预测模型。采用主成分分析方法对NWP各指标进行降维处理,得到包含较多信息量的维数较少的NWP主成分分量,运用BP神经网络和GRNN神经网络对提前量为4 h的风速进行建模预测。
1 多位置NWP数据信息描述
为了覆盖风电场更大范围的气象数据,气象局提供了某风电场典型位置的NWP数据,如图1所示。该数据模型的基本特征如下:
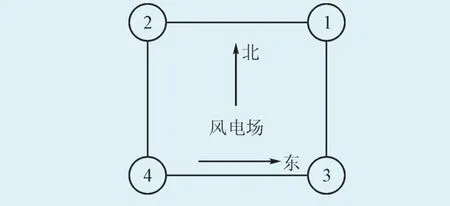
图1 风电场典型位置的NWP数据Fig.1 NWP data of the typical location of w ind farm
每个位置包含10个参数信息,如表1所示。

表1 单个位置的NWP信息Tab.1 Data description of the NWP model
气象局提供未来72 h的NWP信息,每天进行一次更新,时间分辨率为15 min。
由于该风电场NWP数据包含4个位置,每个位置包含10个参数信息,因此每一时刻共含40维数据(12维风速数据、12维风向数据、12维气温数据和4维气压数据)。经分析发现,每个指标的多维数据间存在较强的相关性,因而所得的统计数据反映的信息在一定程度上有重叠。在用神经网络方法研究多变量问题时,变量太多会增加计算量和增加分析问题的复杂性,但希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。主成分分析正是适应这一要求产生的,是解决这类问题的理想工具。
2 主成分分析
主成分分析就是把原来多个指标变量转换为少数几个相互独立的综合指标变量的统计方法。通过全面分析各项指标所携带的信息,从中提取一些潜在的综合性指标,使问题变得比较简单直观。
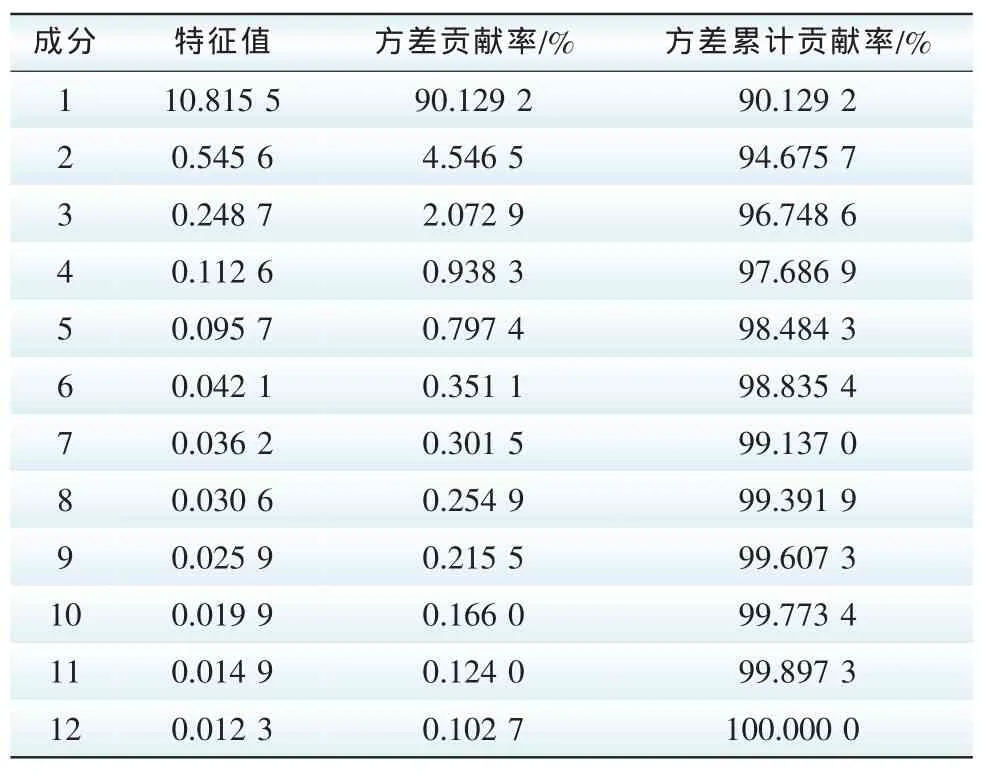
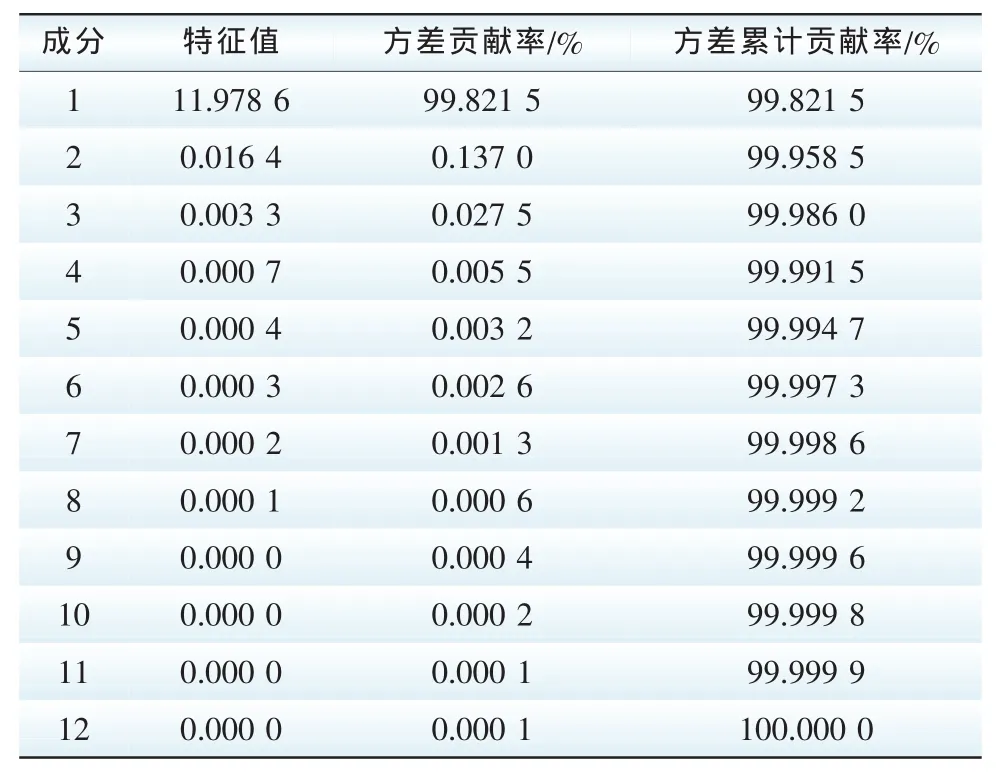
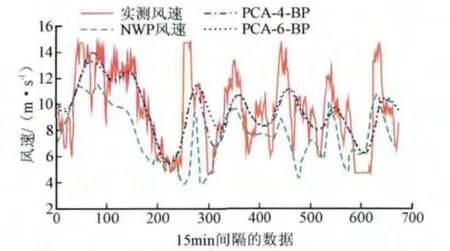
主成分分析思路的数学表示:设X1,X2,…,Xp是原始变量,需要求变量Y1,Y2,…,Ym,满足m 设原始变量X1,X2,…,Xp的观测n次数据矩阵为 1)将原始数据标准化,即对同一变量减去其均值再除以标准差,以消除量纲影响。 2)求相关系数矩阵M。 且有mij=mji,mii=1。 3)求M的特征值及特征向量。根据M的特征方程|M-λE|=0,可求得M的p个特征值λj(j=1,2,3,…,p),λ1≥λ2≥…≥λp≥0,以及相应的特征向量Uj=(U1j,U2j,…,Upj)(j=1,2,…,p)。则提取的主成分记为Yj=Uj,即 4)确定主成分的个数m。 式中,R为累计贡献率下限,需根据实际问题确定,符合上式的前m个主成分,包含了绝大部分的信息,后面其他的主成分就可以舍弃。 5)确定各主成分的权重。以各主成分的方差贡献率作为主成分的权重来计算综合得分。 研究对象为黑龙江某风电场,研究数据采用该风电场2012年2月份共29天的全线风速实测数据及多位置NWP数据,时间间隔均为15 min,共计2784组数据。由于风力发电机的输出功率直接受风速和空气密度的影响,而空气密度将受气温、气压、湿度等气象因素的影响,选取风速、风向、气温、气压4个指标作为神经网络输入。按照2.1小节主成分计算步骤分别对12维风速向量、12维风向向量、12维气温向量和4维气压向量进行主成分提取。计算各指标标准化后的相关系数矩阵M,M的特征值、相应的单位特征向量及贡献率,并依据累积贡献率提取主成分。 主成分的选择方法有3种:1)定义一个需由主成分集合达到的累计贡献率下限,这个下限需根据实际问题来确定,其取值范围可选为[75%,95%][13],本文选取R=85%;2)检查方差相对于主成分个数的散点图,并选择图形接近于水平的点对应的成分个数;3)交叉验证,选取使预测误差最小的主成分个数。 3.1.1 风速主成分提取 风速主成分计算结果如表2所示,图2是方差相对于主成分个数的散点图。观察表2和图2,按照主成分个数选取的第一种方法,可得主成分个数为1;按照第二种方法,可得主成分个数为2;第三种方法需根据最终的预测效果来决定风速主成分个数。 3.1.2 风向主成分提取 风向主成分计算结果如表3所示,图3是方差相对于主成分个数的散点图。观察表3和图3,按照主成分个数选取的第一种方法,可得主成分个数为1;按照第二种方法,可得主成分个数为2;第三种方法需根据最终的预测效果来决定风向主成分个数。 3.1.3 气温主成分提取 气温主成分计算结果如表4所示,图4是方差相对于主成分个数的散点图。观察表4,由于第一主成分的贡献率已达99%以上,所以仅选第一主成分即可,则气温主成分个数为1。 表2 特征值、方差相关统计数据Tab.2 Eigenvalue and principle com ponent contribution rates 图2 方差相对于成分个数的散点图Fig.2 The scatter of variances relative to the number of com ponent 表3 特征值、方差相关统计数据Tab.3 Eigenvalue and principle com ponent contribution rates 图3 方差相对于成分个数的散点图Fig.3 The scatter of variances relative to the number of com ponent 表4 特征值、方差相关统计数据Tab.4 Eigenvalue and princip le component contribution rates 图4 方差相对于成分个数的散点图Fig.4 The scatter of variances relative to the number of com ponent 3.1.4 气压主成分提取 气压主成分计算结果如表5所示,图5是方差相对于主成分个数的散点图。观察表5,由于第一主成分的贡献率已达99%以上,所以仅选第一主成分即可,则气压主成分个数为1。 经过主成分提取,12维的风速向量降低到1维或2维,第一、二主成分分量分别记为VPCA1和VPCA2;12维的风向向量降低到1维或2维,第一、二主成分分量分别记为DPCA1和DPCA2;12维的气温向量降低到1维,第一主成分分量记为DPCA1;4维的气压向量降低到1维,第一主成分分量记为PPCA1。各主成分分量表达式见表6。 表5 特征值、方差相关统计数据Tab.5 Eigenvalue and principle com ponent contribution rates 图5 方差相对于成分个数的散点图Fig.5 The scatter of variances relative to the number of com ponent 表6 各主分量表达式Tab.6 The expression of each principal com ponent 选取VPCA1、DPCA1、TPCA1、PPCA1这4个主成分分量作为预测模型的输入,记为PCA-4维;另选VPCA1、VPCA2、DPCA1、DPCA2、TPCA1、PPCA1这6个主成分分量作为预测模型的输入,记为PCA-6维;预测模型选择BP神经网络和GRNN神经网络。分别研究基于PCA-4维数据的超短期风速预测模型和基于PCA-6维数据的超短期风速预测模型,根据主成分个数选取的第三种方法,比较二者的预测精度,进而确定最终的主成分个数。 对2012年2月4日到2月10日共7天的风速进行预测,时间间隔为15 min,共计672组数据。预测时段为4 h,训练时段分别为1 h、2 h、3 h、4 h、8 h、12 h、16 h、20 h和24 h。以持续模型预测的风速和NWP风速的平均相对误差曲线作为对照组。预测误差结果如图6所示。 图6 不同训练时段的各模型平均相对误差曲线Fig.6 Error statistics for different training periods of different prediction models 由图6可知,随着训练时段增长,训练样本数目增多,预测误差呈上升趋势,训练时段为1 h的各模型预测精度最高,故选训练时段为1 h。可见对于提前4 h的超短期预测,提前1 h的训练样本与预测样本的相关度最高,预测效果最好。对2012年2月4日至2月10日的每4 h风速时间序列进行滚动预测,时间间隔为15 min,结果如图7和8所示。持续模型预测时间点的风速值等于预测时间点前4 h的实测风速值。从图中可以看出,NWP风速与实测风速的变化趋势基本一致,幅值相差较大,训练后的神经网络较好的拟合了二者之间的变换关系,在幅值和变化趋势上更接近实测风速。 图7 预测时间点前4 h的BP模型的风速预测曲线Fig.7 The 4 h-ahead prediction of the w ind farm speed by BP 图8 预测时间点前4 h的GRNN模型的风速预测曲线Fig.8 The 4 h-ahead prediction of the w ind farm speed by GRNN 采用平均相对误差(MRE)指标来衡量各模型的预测结果,如表7所示。可以看出,这7天中PCA-4-GRNN模型预测效果最好,其预测误差比NWP风速降低了7.21%,比持续模型预测风速降低了11.63%,六维模型的预测精度均比四维模型的预测精度差,说明输入数据包含的成分越多,不一定越有利于提高预测精度。 表76种预测模型的MRE对比Tab.7 Error statistics of 6 different prediction models 本文对基于多位置NWP的超短期风速预测进行了研究,提出基于主成分分析与神经网络结合的超短期风速预测模型。由于将多位置NWP的全部信息输入神经网络会显著增加网络的计算量和问题的复杂性,本文采用主成分分析方法,对各指标的数据进行主成分提取,有效降低了神经网络的输入维数,分别采用BP神经网络和GRNN神经网络对提前量为4 h的超短期风速进行建模预测,实验结果显示PCA-4-GRNN模型具有更高的预测精度。 [1] DAMOUSIS I G,ALEXIADIS M C,THEOCHARIS J B,et al.A fuzzy model for wind speed prediction and power generation in wind parks using spatial correlation[J].IEEE Transaction on Energy Conversion,2004,19(2):352 -361. [2] 连文莉,黄成辰,吕昌霖.采用时间序列预测风电场出力[J].电网与清洁能源,2011,27(12):112-117.LIAN Wenli,HUANG Chengchen,L譈 Changlin.Wind power output prediction based on time series[J].Power System and Clean Energy,2011,27(12):112-117(in Chinese). [3] 张学清,梁军.风电功率时间序列混沌特性分析及预测模型研究[J].物理学报,2012,61(19):70-81.ZHANG Xueqing,LIANG Jun,Chaotic characteristics analysis and prediction model study on wind power time series[J].Acta Physica Sinica,2012,61(19):70-81(in Chinese). [4] 赵攀,戴义平,夏俊荣,等.卡尔曼滤波修正的风电场短期功率预测模型[J].西安交通大学学报,2011,45(5):47-51.ZHAO Pan,DAI Yiping,XIA Junrong,et al.A kalman filter based correction model for short-term wind power prediction[J].Journal of Xi’an Jiaotong University,2011,45(5):47-51(in Chinese). [5] 时庆华.基于卡尔曼滤波和神经网络的短期风电功率预测[D].南京:东南大学,2010. [6] 师洪涛,杨静玲,丁茂生,等.基于小波—BP神经网络的短期风电功率预测方法[J].电力系统自动化,2011,35(16):44-48.SHI Hongtao,YANG Jingling,DING Maosheng,et al.A short-term wind power prediction method based on wavelet decomposition and BP neural network[J].Automation of Electric Power Systems,2011,35(16):44-48(in Chinese). [7] 张靠社,杨剑.基于Elman神经网络的短期风电功率预测[J].电网与清洁能源,2012,28(12):87-91.ZHANG Kaoshe,YANG Jian.Short-term wind power forecasting based on the elman neural network[J].Advances of Power System&Hydroelectric Engineering,2012,28(12):87-91(in Chinese). [8] 黄金花.基于神经网络的风电场短期风电功率预测研究[D].南京:东南大学,2010. [9] 王子赟,纪志成.基于灰色-辨识模型的风电功率短期预测[J].电力系统保护与控制,2013(12):79-85.WANG Ziyun,JI Zhicheng.Grey-identification model based wind power generation short-term prediction[J].Power System Protection and Control,2013(12):79-85(in Chinese). [10] 孟祥星,田成微,冬雷,等.灰色理论用于风力发电容量中长期预测的研究[J].电力系统保护与控制,2011,39(21):81-85.MENG Xiangxing,TIAN Chengwei,DONG Lei,et al.A study of grey theory used in prediction of medium and long-term wind power generation[J].Power System Protection and Control,2011,39(21):81-85(in Chinese). [11] 牛晨光,游晓科,赵震云,等.风电场发电功率短期预测组合模型研究[J].华北电力大学学报,2012,39(3):29-34.NIU Chenguang,YOU Xiaoke,ZHAO Zhenyun,et al.Study on the combination model of short-term wind power generation prediction[J].Journal of North China Electric Power University,2012,39(3):29-34(in Chinese). [12] 张国强,张伯明.基于组合预测的风电场风速及风电机功率预测[J].电力系统自动化,2009,33(18):92-95.ZHANG Guoqiang,ZHANG Boming.Wind speed and wind turbine output forecast based on combination method[J].Automation of Electric Power Systems,2009,33(18):92-95(in Chinese). [13] SANDHYA S.神经网络在应用科学和工程中的应用—从基本原理到复杂的模式识别[M].史晓霞译.北京:机械工业出版社,2009:7.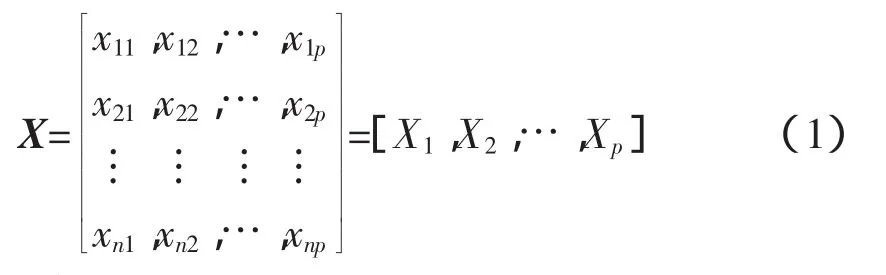




3 实例分析
3.1 各因素主成分提取







3.2 预测时段为4 h的预测结果对比



4 结语

