多场景随机风速条件下的配电网风电机组选址定容

潘明炜，杜松怀，苏娟

（中国农业大学信息与电气工程学院，北京 100083）

随着环境污染和能源危机日益严重，以风力发电为代表的可再生能源发电由于清洁环保的优势得到了快速发展。风力发电按规模大小可分为大规模集中接入输电网的风电场和以分布式电源形式接入配电网的风电机组（以下简称风机）。风机接入配电网运行使得配电网由单电源辐射型网络变成多电源网络，由于风机出力的波动性和间歇性的特点，会对配电网的潮流分布、系统稳定等方面产生影响，其影响程度与风机接入的位置和容量关系密切[1-2]，因此在考虑风速随机性的情况下，对接入配电网的风机进行选址定容是非常必要的。

近年来，分布式电源（DG）接入配电网的选址定容的研究已经取得较多成果。文献[3]提出以DG注入后网损最小为目标函数的DG规划模型。文献[4]在原有网络负荷值不变的情况下，以系统网损最小为目标函数研究了单台DG最优接入位置。文献[5]以网损最小为目标函数使用量子粒子群算法确定DG的最优位置和容量。文献[6]建立以社会效益最大化为目标的DG与配电网规划协调规划模型。文献[7]以投资成本和损耗成本最低为目标函数，在配电网扩展规划中进行DG的选址定容。文献[8]在考虑分布式发电的经济性和安全性的基础上，建立了以分布式发电投资成本最小、系统网损最小和静态电压稳定裕度最大为优化目标的多目标规划模型。文献[9]应用机会约束规划的方法建立了以独立发电商收益最大为目标函数的分布式风电源接入配电网的规划模型。文献[10]建立了以年综合费用最小为目标的风机机会约束规划模型。文献[11]在DG选址定容中提出了一种实用的DG候选位置选取方法以缩小搜索空间。

由上可见，大多数规划模型的研究对象主要针对可灵活控制的DG，而风机出力具有间歇性和随机性，传统的规划模型并不能完全适用于风机的选址定容问题。另一方面，实际配电网中不同地区的风速情况是不同的，风机规划的模型需要考虑实际风速情况。

针对上述问题，本文建立了多场景概率分布条件下的风机出力模型，预置配电网节点的风速参数来考察实际配电网风速情况对风机接入配电网规划的影响。基于风机多场景概率分布出力，以系统有功损耗改善率和系统静态电压稳定裕度值为评价指标选取风机接入配电网的候选位置。在不考虑新增负荷节点的情况下，建立了以风机投资成本费用、风机运行和维护费用及系统有功损耗费用最小为目标的配电网风机规划模型，利用IEEE33节点系统对提出的模型和方法进行验证。

1 多场景概率分布条件下的风机出力模型

1.1 风速概率密度分布

研究表明，一个地区风速的概率密度一般服从威布尔分布[12]。假设风速为随机变量，其概率密度函数为

式中，v为风速；c为尺寸参数；k为形状参数，取值在1.7～2.4之间[13]。

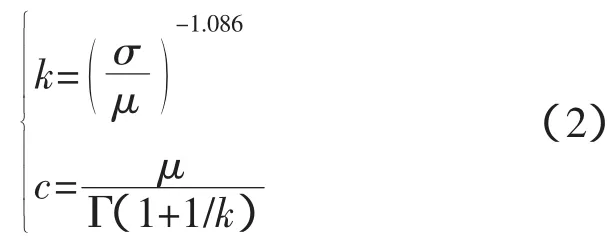
式中，σ为统计时间内风速标准差；μ为统计时间内的风速期望；Γ为伽马函数。

1.2 多场景概率分布条件下的风机功率特性

风机的输出功率与风速和自身的功率特性密切相关[14]，风机输出功率PW可由下式计算

式中，vci、vr、vco、Pr分别为风机的切入风速、额定风速、切出风速和额定输出功率；k1=Pr（/vr-vc）i和k2=-k1vci均为常数。

风机输出功率可分为3个典型场景。

1）欠额定输出场景，若取风速的离散化步长为（vr-vc）i/N，则可将风速从vci到vr等分N为个风速场景。设v（i）为离散化风速值，FV（i）为对应的风速概率，PW（i）为风速v（i）对应的风机输出功率，FW（i）为风机输出功率PW（i）对应的概率，其值分别为[15-16]

式中，i为场景编号，i=1，2，…，N。

2）零输出场景，定义此时风速为第N+1个场景，则对应的风速场景概率为

此场景下风机输出功率及对应概率为

3）额定输出场景，定义此时风速为第N+2个场景，则对应的风速场景概率为

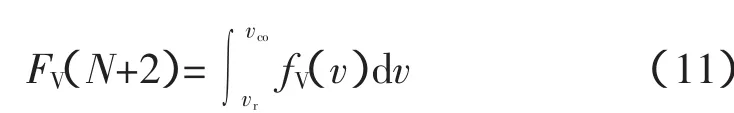
此场景下风机输出功率及对应概率为

对风力发电来说，风机往往采用结构较简单的异步发电机，在运行过程中要从系统吸收无功功率[17]，假设风机采用恒功率因数运行，则风机的无功出力QW为

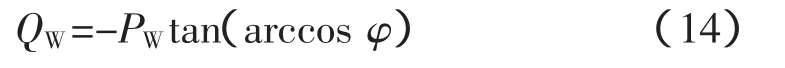
式中，cos φ为风机运行的功率因数。

1.3 地区风速参数预置

风机输出功率的随机波动主要源于风速的随机波动。考虑到实际配电网系统的供电范围较大，利用威布尔分布拟合风机出力时不同地区的风速参数应不同。

本文提出将已有配电系统的负荷节点按照相邻2至4个划分为一个地区，使用双参数威布尔分布预置各个地区的风速参数，即参数c和k，模拟系统实际风速情况，并计算出接入各地区风机的多场景概率分布输出。

对于预置的威布尔分布的2个参数，在实际规划中可利用历史风速数据估计得出。

2 风机多场景概率分布出力下的候选位置确定

配电网中风机可选布点较多，导致在求解过程中计算量大，易产生不可行解。本文在文献[11]所提出的DG候选位置选取方法的基础上，基于风机多场景概率分布出力，以减小系统有功损耗和改善系统静态电压稳定性两方面建立风机接入位置的评价指标。

2.1 风机接入位置的评价指标

2.1.1 系统有功损耗改善率

为了量化风机多场景输出对配电网损耗的改善情况，引入系统有功损耗改善率指标λP[18]，其值越小表明风机接入对系统降损效果越好，其定义如下

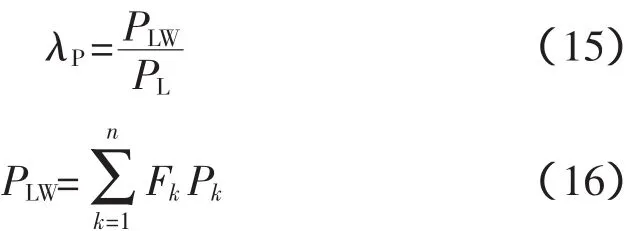
式中，PLW和PL分别为安装风机后和安装风机前的系统网损，kW；n为风机输出的场景数；Fk为第k个输出场景的概率；Pk为第k个输出场景下的系统有功损耗。

2.1.2 系统静态电压稳定裕度值

本文选择指L标来衡量配电系统的静态电压稳定性[19]。图1所示的简单电力系统中：R和X分别为线路的电阻和电抗；Pa和Qa分别为首端的有功功率和无功功率；Pb和Qb分别为末端的有功功率和无功功率；Ua和Ub分别为首端和末端的母线电压。

图1 简单电力系统Fig.1 The simp le power system

则配电网线路的电压稳定指标为

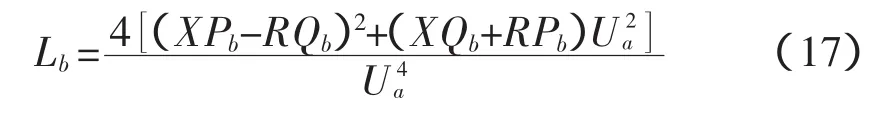
式中，Lb表示第b条支路的电压稳定指标，定义所有支路电压稳定指标中的最大者为系统电压稳定指标L，即

式中，N为配电系统节点总数。对应L的支路为系统的最薄弱支路，根据L值与临界值1.0的距离来判断系统电压稳定的程度。

引入系统静态电压稳定裕度值指标λL，其值距离1.0的距离越大表明风电接入对系统静态电压稳定性改善程度越好，其定义如下

式中，n为风机输出的场景数；Fk为第k个输出场景的概率；Lk为第k个输出场景系统静态电压稳定裕度值。

2.2 风电接入候选位置的确定方法

基于风机多场景概率分布出力，量化风机接入对配电网有功损耗和系统静态电压稳定性的影响，结合实际配电网结构及实际风速情况，选取风机候选位置。

1）将各节点接入风机后的系统有功损耗改善率进行排序，选取改善较好的前40%的节点；

2）将各节点接入风机后的系统静态电压稳定裕度值进行排序，选取裕度值与1.0距离较大的前40%的节点；

3）由于风机布局不宜集中，同时考虑到实际风速对风机出力的影响，在之前已选出分布过于集中的节点中，选择指标数值排序靠前且平均风速期望值较大的节点作为候选节点，以保证最好的风机出力；

4）若分支线路没有风机接入候选位置，则增加该分支线路中系统有功损耗改善率和系统静态电压稳定裕度值最好的节点作为风机候选位置。

3 配电网风机选址定容规划模型

3.1 目标函数

以配电网年综合费用最小[7，10]为目标，建立配电网风机选址定容规划模型，目标函数为：

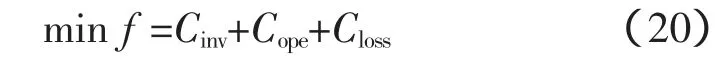
式中，Cinv为风机投资成本费用；Cope为风机运行和维护费用；Closs为系统有功损耗费用；

3.1.1 风机投资成本费用表示为

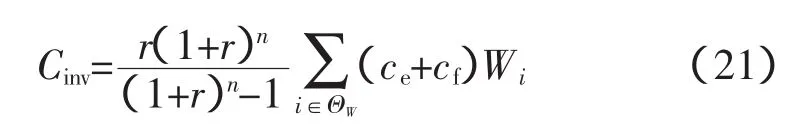
式中，r为贴现率；n为风机经济使用年限；ΘW为风机接入的节点集；ce为风机单位容量固定投资费用，元/kW；cf为风机单位容量安装费用，元/kW；Wi为第i个节点风机的装机容量，kW。

3.1.2 风机运行和维护费用表示为

式中，cr为风机单位发电量的运行和维护费用，元/kW·h；ΘW为风机接入的节点集；Ei为接入第i个节点风机的年发电量期望值，可由风机输出功率和风速

3.1.3 有功损耗费用表示为

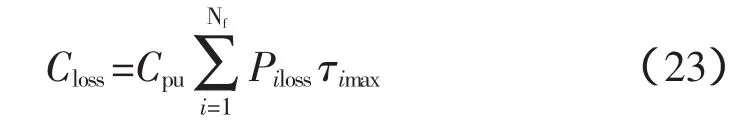
式中，Cpu为单位电价，元/kW·h；Nf为网络馈线总数；Piloss为第i条支路的有功损耗值，kW；τimax为第i条支路的年最大负荷损耗小时数，h。

3.2 约束条件

1）等式约束条件为潮流方程

式中，Pi、Qi分别为节点i注入的有功功率和无功功率；Ui、Uj分别为节点i和节点j的电压幅值；Θi为与节点i相连的节点集合；Gij和Bij分别为节点导纳矩阵的实部和虚部；θij为节点i和节点j之间的相角差。

2）不等式约束条件为节点电压限制、支路功率限制、风机接入节点风机装机容量限制、风机装机总容量占系统总负荷比例限制、风机接入位置个数限制，即

式中，U为节点电压幅值；Umin和Umax为节点电压上下限；Pimax为支路有功功率上限；Wimax为第i个待选节点允许安装的风机最大容量；ΘW为风机接入的节点集；ρ为系统风机装机总容量占系统最大总负荷的比例上限；Sload为系统的总负荷；NWmax为系统允许风机接入的最大位置个数。

3.3 求解策略

本文采用遗传算法优化风机接入的位置和容量。

3.3.1 染色体编码

采用二进制数编码来表示每个候选位置上风机接入的台数。

3.3.2 规划流程

1）输入待规划配电网原始数据及节点风速参数。

2）模拟网络各节点风机多场景概率分布出力，使用前推回代法依次对各节点接入等容量风机后的配电网络进行潮流计算。

3）根据潮流计算获得的支路功率和节点电压等数据，计算不同接入位置时配电网系统有功损耗改善率和系统静态电压稳定裕度值，结合实际配电网结构及实际风速情况，选取风机候选位置。

4）对决策变量进行编码，预设种群大小、迭代次数、交叉率、变异率等。

5）生成初始种群，并设置当前迭代次数G=1。6）对接入风机的配电网进行潮流计算。

7）计算目标函数，得到个体适应值，对违反约束条件的个体在其适应值上添加相应的罚函数。

8）对前代种群进行遗传操作，包括精英保留、选择、交叉、变异等操作，产生新种群。

9）判断G是否已达到预设的最大迭代次数，若G>Gmax，则结束计算，输出最优解，否则G=G+1，转向步骤6）。

4 算例分析

4.1 算例介绍

本文采用IEEE33节点配电网测试系统[20]作为算例对风机接入配电网的位置及容量进行规划。系统首端电压12.66 kV，总负荷为3715l W+2300 kvar。系统风机接入装机总容量占系统最大总负荷比例上限为30%[11]，取系统风机允许安装装机总容量为200 kW ～1100 kW，每个候选位置风机最大允许安装容量取1100 kW。设系统各节点风速服从双参数威布尔分布，参数值见表1[10，16，21]，其中μ通过k和c计算得出，反映平均风速期望，m/s。单台风机额定容量为100 kW，切入风速、额定风速和切出风速分别为3 m/s，13 m/s，20 m/s，功率因数取0.95。风机单位造价5000元/kW，安装成本1200元/kW，经济使用年限为15 a，贴现率为0.08，运行和维护费用为60元/kW·h，年最大负荷损耗小时数为4000 h，电价为0.5元/kW·h。节点电压允许范围为0.95 ～1.05（标幺值）。

表1 IEEE33系统节点风速参数值Tab.1 W ind velocity parameter values of IEEE 33 system

4.2 风机候选位置调整与确定

在IEEE33节点配电系统的不同位置接入风机进行测试，分别得到接入风机容量占系统最大总负荷比例为10%、15%和20%时的系统有功损耗改善率和系统静态电压稳定裕度值，如图2、3所示。

图2中3种占比的风机容量接入系统后，系统有功损耗改善率曲线基本走势相同。可以看出风机接入位置越靠近线路偏末端有功损耗改善情况越好，但不同容量对改善程度有所差异，可见系统有功损耗改善率能够有效反映风机接入对系统有功损耗影响的经济效益。

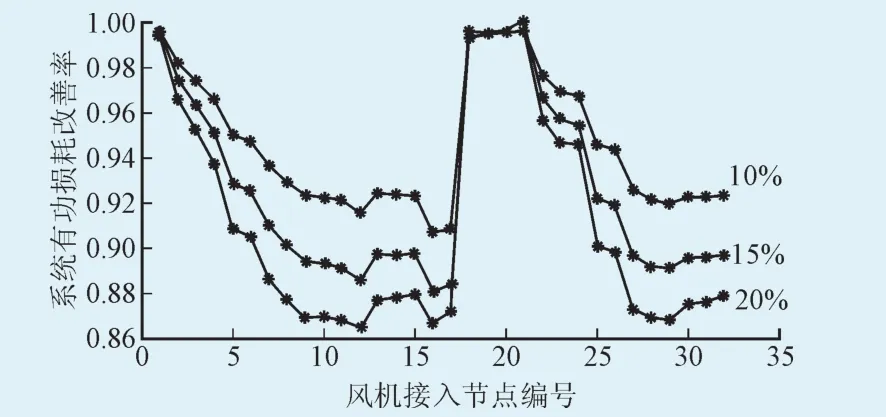
图2 风机接入IEEE33系统不同位置的系统有功损耗改善率Fig.2 Active power loss im provement index according to the change of w ind turbine location on IEEE 33 system

图3 风机接入IEEE33系统不同位置的系统静态电压稳定裕度值Fig.3 Static voltage stability index according to the change of w ind turbines location on IEEE 33 system

图3中3种占比的风机容量接入系统后，系统静态电压稳定裕度值曲线基本走势相同。可以看出风机接入位置越靠近线路偏末端系统静态电压稳定裕度值距离1.0越远，说明风机接入能有效提高系统静态电压稳定性，系统静态电压稳定裕度值可用来评估风机接入对系统的可靠性的影响。

根据上述选取风机接入候选位置的方法，对以占系统最大总负荷比例为15%的风机容量接入IEEE33系统不同位置时的系统有功损耗改善率及系统静态电压稳定裕度值分别进行排序，结合IEEE33配电系统结构及预置的实际风速情况，选取风机接入候选位置：

1）选取系统有功损耗改善率较小的节点：16、17、12、29、11、28、10、9、30、31、27、14、32；

2）选取系统静态电压稳定裕度值距离1.0较大的节点：29、28、27、16、17、30、31、32、12、11、9、10、8；

3）对上述分布过于集中的候选节点进行筛选，候选节点集缩小为：17、12、29、9、31、14；

4）在没有候选节点的分支中增加的节点：19、24；

最终确定的风机接入候选位置为：17、12、29、9、31、14、19、24，如图4所示。

图4 风机接入候选位置Fig.4 Candidate positions of w ind turbines

为了考察系统内不同地区的风速参数对风机接入配电网规划的影响，同时选取了IEEE33系统内所有节点风速参数按照统一的k和c值3.0和9.0设定时的风机接入候选位置，风机的指标和选取方法同上。选出的风机接入候选节点为：14、12、16、9、30、32、19、24。

4.3 规划结果分析

根据所提出的模型和算法，获得可行的配电网风机规划方案如表2所示。

表2 风机接入规划方案Tab.2 W ind turbines integrated p lanning schemes

方案1和方案2为预置风速参数后规划出的可行方案，从表2数据中可以看出：方案1较方案2的风机运行维护费用小，但有功损耗费用则偏大。实际规划人员可根据风机规划特定的目的和需求选取优化方案。本文综合考虑总成本方案1最小，取方案1为最优方案。方案3为配电系统各节点风速参数为统一值时规划出的可行方案，说明本文模型同样适用于此类情况，结合候选位置的选择情况可以看出，不同的风速参数对风机接入候选位置的选定有较大影响，按照统一风速参数规划出的结果并不能完全符合实际情况，预置风速参数可以有效地避免规划出与实际风速情况不匹配的风机选址，可使规划结果更好地为工程项目服务。

5 结论

本文建立了基于多场景概率分布条件下的风机出力模型，以系统有功损耗改善率和系统静态电压稳定裕度值作为风机接入配电网候选位置的为评价指标。建立了以风机投资成本费用、风机运行和维护费用及系统有功损耗费用最小为目标的配电网风机规划模型，预置IEEE33节点系统各节点风速指标并利用该系统对提出的模型和方法进行仿真研究，得到以下结论：

1）依据风速概率密度分布建立风机多场景概率分布出力模型，能比较充分的考虑风速随机性对风机出力的影响，提高了风机输出模型的精确性；

2）系统有功损耗改善率和系统静态电压稳定裕度值，能有效反映风机接入配电网的经济效益和可靠性指标，以此选取的风机接入候选位置有效可靠；

3）通过预置配电系统风速参数可以有效地避免规划出与实际风速情况不匹配的风机选址，使规划结果更加符合实际的风速参数，更好地为工程项目服务。

[1] 李黎.分布式发电技术及其并网后的问题研究[J].电网与清洁能源，2010，26（2）:55-59.LI Li.A study on distributed generation and its effects in power system[J].Power System and Clean Energy，2010，26（2）:55-59（in Chinese）.

[2] 谷永刚，王琨，张波.分布式发电技术及其应用现状[J].电网与清洁能源，2010，26（6）:38-43.GU Yonggang，WANG Kun，ZHANG Bo.Distributed generation technologies and their current applications[J].Power System and Clean Energy，2010，26（6）:38-43（in Chinese）.

[3] 陈海焱，陈金富，杨雄平，等.配电网中计及短路电流约束的分布式发电规划[J].电力系统自动化，2006，30（21）:16-21.CHEN Haiyan，CHEN Jinfu，YANG Xiongping，et al.Planning for distributed generation in distribution network with short-circuit current constrains[J].Automation of Electric Power Systems，2006，30（21）16-21（in Chinese）.

[4] NARESH ACHARYA，PUKAR MAHAT，MITHULANANTHAN N.An analytical approach for DG allocation in primary distribution network[J].International Journal of Electrical Power&Energy Systems，2006，28（10）:669-678.

[5] 杨宝杰，海晓涛.基于量子粒子群算法的配电网分布式电源选址和定容[J].陕西电力，2011，38（12）:24-27.YANG Baojie，HAI Xiaotao.Siting and sizing of distributed generation based on quantum-behaved particle swarm optimization algorithm[J].Shaanxi Electric Power，2011，38（12）:24-27（in Chinese）.

[6] 高军彦，麻秀范，凡鹏飞.计及分布式发电的配电网协调规划整体框架与模型[J].电网与清洁能源，2008，24（10）:12-16.GAO Junyan， MA Xiufan， FAN Pengfei.A global framework and model of distribution network coordinated planning including distributed generation[J].Power System and Clean Energy，2008，24（10）:12-16（in Chinese）.

[7] 王成山，陈恺，谢莹华，等.配电网扩展规划中分布式电源的选址和定容[J].电力系统自动化，2006，30（3）:38-43.WANG Chengshan，CHEN Kai，XIE Yinghua，et al.Siting and sizing of distributed generation in distribution network expansion planning[J].Automation of Electric Power Systems，2006，30（3）:38-43（in Chinese）.

[8] 周巧俏，汤云岩，海晓涛.基于改进自适应遗传算法的分布式电源的选址和定容[J].陕西电力，2010，38（6）:40-44.ZHOU Qiaoqiao，TANG Yunyan，HAI Xiaotao.Location and sizing of distributed generation based on improved self-adaptive gentic algorithm[J].Shaanxi Electric Power，2010，38（6）:40-44（in Chinese）.

[9] 张节潭，程浩忠，姚良忠，等.分布式风电源选址定容规划研究[J].中国电机工程学报，2009，29（16）:1-7.ZHANG Jietan，CHENG Haozhong，YAO Liangzhong，et al.Study on siting and sizing of distributed wind generation[J].Proceedings of the CSEE，2009，29（16）:1-7（in Chinese）.

[10] 张沈习，陈楷，龙禹，等.基于混合蛙跳算法的分布式风电源规划[J].电力系统自动化，2013，37（13）:76-82.ZHANG Shenxi，CHEN Kai，LONG Yu，et al.Distributed wind generator planning based on shuffled frog leaping algorithm[J].Automation of Electric Power Systems，2013，37（13）:76-82（in Chinese）.

[11] 唐巍，薄博，丛鹏伟，等.含分布式发电接入的农村电网多目标规划[J].农业工程学报，2013，29（25）:132-137.TANG Wei， BO Bo， CONG Pengwei， et al.Multiobjective planning of rural power network incorporating distributed generation[J].Transactions of the Chinese Society of Agricultural Engineering，2013，29（25）:132-137（in Chinese）.

[12] KARAKI S H，CHEDID R B，RAMADAN R.Probabilistic performance assessment of autonomous solarwind energy conversion systems[J].IEEE Transactions on Energy Conversion，1999，14（3）:766-772.

[13] 朱德臣，汪建文.风工况双参数威布尔分布k值影响研究[J].太阳能，2007（6）:34-36.ZHU Dechen，WANG Jianwen.Study k value impact of wind conditions two-parameter weibull distribution[J].Solar Power，2007（6）:34-36（in Chinese）.

[14] BOWDEN G J，BARKER P R，SHESTOPAL V O，et al.The weibull distribution function and wind power statistics[J].Wind Engineering，1983（7）:85-98.

[15] MEHRTASH A，WANG P，GOEL L.Reliability evaluation of restructured power systems with wind farms using equivalent multi-state models[C]//Probabilistic Methods Applied Power Systems（PMAPS）.Singapore:Probabilistic Methods Applied Power Systems（PMAPS），2010:716-721.

[16] 丛鹏伟，唐巍，张璐，等.基于机会约束规划考虑DG与负荷多状态的配电网重构[J].电网技术，2013，39（9）:2573-2579.CONG Pengwei，TANG Wei，ZHANG Lu，et al.Chanceconstrained programming based distribution network reconfiguration considering multi-states of distributed generation and load[J].Power System Technology，2013，39（9）:2573-2579（in Chinese）.

[17] 陈海焱，陈金富，段献忠.含风电机组的配网无功优化[J].中国电机工程学报，2008，28（7）:40-45.CHEN Haiyan，CHEN Jinfu，DUAN Xianzhong.Reactive power optimization in distribution system with wind power generators[J].Proceedings of the CSEE，2008，28（7）:40-45（in Chinese）.

[18] SINGH D，VERMA K S.Multiobjective optimization for DG planning with load models[J].Power Systems，IEEE Transactions on，2009，24（1）:427-436.

[19] 刘健，毕鹏翔，董海鹏.复杂配电网简化分析与优化[M].北京:中国电力出版社，2002.

[20] BARAN M E，WU F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Transactions on Power Delivery，1989，4（2）:1401-1407.

[21] 龚伟俊，李为相，张广明.基于威布尔分布的风速概率分布参数估计方法[J].可再生能源，2011，29（6）:20-23.GONG Weijun，LI Weixiang，ZHANG Guangming.The estimation algorithm on the probabilistic distribution parameters of wind speed based on weibull distribution[J].Renewable Energy Resources，2011，29（6）:20-23（in Chinese）.