航班延误关键影响因素及影响程度识别——基于动态排队模型的分析

杨秀云，王 军，2，何建宝

（1．西安交通大学 经济与金融学院，陕西 西安 710061；2．西安财经学院 高等职业技术学院，陕西 西安 710061）

航班延误关键影响因素及影响程度识别
——基于动态排队模型的分析

杨秀云1，王 军1，2，何建宝1

（1．西安交通大学 经济与金融学院，陕西 西安 710061；2．西安财经学院 高等职业技术学院，陕西 西安 710061）

通过对航班运行流程闭环不同阶段的分解分析，识别出航班延误的关键原因包括流量控制、军事活动、天气等不可控因素和安检、旅客、机械故障、机场、公共安全等可控因素。运用数理推导和实证分析，验证了飞机起飞到达服从泊松分布，航班延误符合指数分布。通过构建航班延误总动态排队模型，并基于典型机场数据的模拟仿真分析，证明各因素引发的航班延误频率高低及其影响程度并非完全一一对应。航空公司因素发生频率最高、影响最大；流量控制发生频率较高、影响大；天气因素发生频率较高、影响较大；军事活动发生频率一般，但影响大；机械故障频率较低、影响较大；机场因素频率较低、影响较小。

航班延误；泊松分布；指数分布；排队模型

与其它运输方式相比较，航空运输具有速度快、耗时少、效率高和舒适的特点，因此自1990年以来，航空运输在长途运输方面一直占有绝对优势，保持了两位数的增长。2002—2012年，中国航空旅客运输量从8 594万人次上升到31 936万人次，航空运力投放从602架增加到了1 941架，航班班次从79．25万班次增加到250．2万班次。然而，在中国民用空域有限的条件下，在民航运输由少数高档消费演变为今天的全民大众消费时，市场需求总量和需求质量预期要求不断提高，航空运输各项指标迅速增长，带来的却是航空运输通道的拥挤和不畅，由此导致的航班延误总量和比率持续增加，航班延误投诉率不断攀升。2012年中国航班正常率为74．83%，是近五年来的最低，不正常航班63．0万班次，每天因延误约浪费57万小时，平均每人次耽误40分钟。2013年6月，美国航空数据网站FlightStats公布了世界35家机场和32家航空公司航班的延误率，首都机场和上海浦东机场的延误率分别以81．7%和71．3%在亚洲排名第一和第二，四家航空公司排名包揽倒数四名［1］。据中国消费者协会2010—2011年投诉统计数据反映，航空运输服务已成为服务类投诉增幅最大的行业，投诉增幅居首位，航班延误及其后续服务投诉最多，是消费者最不满意的航空服务。中国消费者协会和民航总局2012年的航空服务消费者调查报告显示，有76．5%的消费者遇到过航班延误，49．5%的消费者对航班延误后的服务不满意。

可见，让航空运输相关部门感到棘手的不仅是航班延误率的增加，还有消费者对航班延误及其后续服务的不满意。这是因为，目前中国只有《民用航空法》、《航班延误经济补偿指导意见》两个法律政策可指导航班延误问题处理，缺少依据航班延误关键影响因素及其影响程度和不同航班延误时长而制定的统一的、权威的、具体的和可操作的相关政策措施，导致许多航班延误问题和顾客投诉问题都不能得到很好的解决。在没有统一政策规定指导下，各个航空公司各施其政，制定出不同的航班延误服务补救依据和标准，有的航空公司为了息事宁人，甚至采取“大闹大赔，小闹小赔”的办法，不仅混淆了旅客对航班延误问题的正确认识，误导他们产生“只要遭遇航班延误，都可要求补偿”的理解，如要求不能得到满足，就采取群体性行为或极端行为危害机场公共安全。

国内外有关航班延误原因的研究，经历了由浅入深、由单一到多重、由单独影响到交互影响的过程，但相关文献较少［2］。Allan S．S．等运用美国纽约纽瓦克国际机场的数据，借助数据库开发工具分析了天气与大规模航班延误的关系，指出不同类型的天气事件，会产生登机、滑出、空中和到达等不同类型的延误［3］。张静建立了瞬时排队模型和模糊线性回归模型，论证了天气与航班延误之间存在高度相关关系［4］。Abdelghany K．F．等运用航班延误的链式模型证明波及延误是航班延误的主要原因［5］。邵维亮基于航班运行仿真方法，分析了航空公司航班计划编制是可以控制的影响航班延误的主要因素［6］。Jarrah A．I．Z．等采用两个最小费用流模型分析了航班延误波及影响和飞机短缺带来的航班延误问题，指出航班计划之间是紧密相连的，一个航班的延误，必然导致后续航班被迫相应延误和延误波及［7］。Liou用人工神经网络模型来估计单个航班离港延误，归纳出影响延误的主要因素是航线、飞机类型、航班顺序和空中交通流量［8］。Georgina S．等运用瓶颈模型和欧洲主要机场的数据，验证了大型航空公司和在机场具有控制力的航空公司能够内部化航班延误，航班延误更多出现在枢纽机场［9］。邢有洪等采用Logit模型分析了航空公司内部因素对航班延误的影响，发现航空公司的偿债能力、盈利能力、客座率以及载运率等对航班延误都有显著影响［10］。邵荃等通过建立贝叶斯网络分析模型，指出航班延误的主要原因有航空公司计划、本站天气、前站天气、旅客、运力调配、前站飞机、航路限制及各自的比重［11］。

总之，已有相关文献较少，且仅识别影响因素或评价少数因素引发延误的频率高低，很少同时识别航班延误的关键影响因素、各因素引发延误的频率及其影响强度，而频率和强度之间并非正向相关关系，有的因素引发延误的频率可能较低但影响强度很大。这也是目前中国航班延误应急及服务补救措施无法统一，进而导致消费者不满和采取极端行为的根本原因。因此，急需运用科学方法，探索航班延误的关键影响因素及其影响程度，为应对航班延误的应急方案设计以及制定行业统一的航班延误服务补救措施提供依据。

一、航班延误原因的一般识别

为了提高飞机利用效率，航空公司的同一架飞机的运行路线往往不是点对点的往返飞行，而是由连续的不同航段组成的一个闭环。在航班运行的闭环中，按照航班延误的表现形式，可把航班延误分为三类：

一是旅客延误，常见的情形有：旅客晚到；登机时旅客不辞而别；旅客证件问题耽误时间；旅客因航班延误等其它服务问题霸占飞机或拒绝登机；旅客随身携带过多行李；突发疾病等。目前，因旅客原因导致的航班延误比例占到3%，已成为航班延误“新的增长点”。

二是排队延误，包括安检排队延误和飞机起飞降落排队延误。安检排队延误是由于机场的服务能力有限或是旅客在一段时间内太过密集而造成的安检不畅，形成很长的排队等待，这与安检站台的服务容量和安检服务效率密切相关，发生的概率相对较低。飞机起飞降落排队延误，是由于起飞或降落航班过多，或是天气、军事活动和流量控制，或者是低效率的地面服务，造成飞机难以立即起飞的地面排队或不能在机场找到降落位置而不得不停留在空中继续盘旋等待排队。这种延误会引起连锁反应，对后续飞机产生较长的排队时间，如果不及时采取措施，就会导致后续所有飞机都延迟起飞或降落，不断累积，形成更大更强的延误波。现阶段，波及延误是占比最高的延误，特别是起飞排队延误。为了弱化这种累计的航班延误波及效应，一般的做法就是在航班运行的每个环节都设置一段时间的缓冲时间。

三是航空公司造成的延误，这是因航空公司自身的运营管控能力或机械故障造成的航班计划安排不当引起的航班延误。

引发上述三种航班延误的因素按照可控与否，可分为不可控因素和可控因素，不可控因素包括流量控制、军事活动、天气等，可控因素包括安检、旅客、机械故障、机场原因和公共安全等，其中可控因素是航班延误研究和治理的重点［9，12］。

根据民航总局2005—2013年航班延误统计数据，造成中国航班延误的关键因素包括流量控制、航空公司、天气、军事活动、机场因素、机械故障以及旅客等因素，综合主要航空公司和主要机场的相关数据，得到各因素引发的延误比例结构见表1。

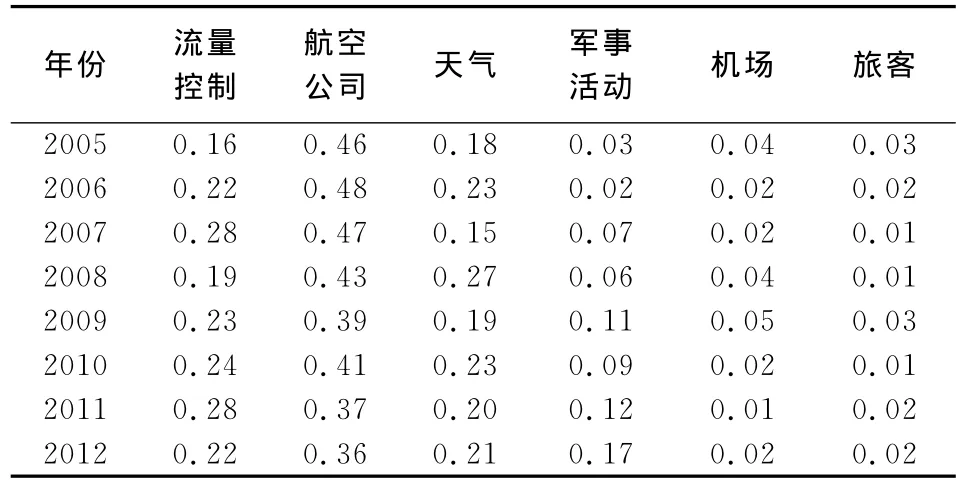
表1 航班延误影响因素比例结构表

这些统计数据仅反映了各关键影响因素引起航班延误发生频率的比重，而没有体现对航班延误的影响程度，因而下面本文将基于航班延误的指数分布验证，构建航班延误的排队模型，探析各个关键影响因素的发生频率及对航班延误的影响程度。

二、航班延误的指数分布验证

泊松分布适用于描述单位时间（或空间）内随机事件发生的次数。如某一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台的候客人数等。机场作为提供航空运输服务的公共基础设施，单位时间内到达和起飞的飞机数量符合泊松分布特征，可以假设机场飞机的起飞和到达都是服从泊松分布。根据概率论，如果一个序列服从泊松分布，那么它的序列间隔服从负指数分布，即如果飞机到达和起飞呈现出泊松分布，可以推导出起飞和到达延误时间服从均值为1／λ，方差为1／λ2的指数分布［13－14］。当然，只要验证到达延误分布服从指数分布，就可间接求证飞机到达分布服从泊松分布，并且求出相应的λ值［15］127－145。

表2是随机收集的2013年3月咸阳机场和首都机场四个样本时间段航班延误时长和数量。通过分析航班延误样本的实际分布和理论指数分布之间的拟合度，来验证航班延误的指数分布假设，验证结果见表3。

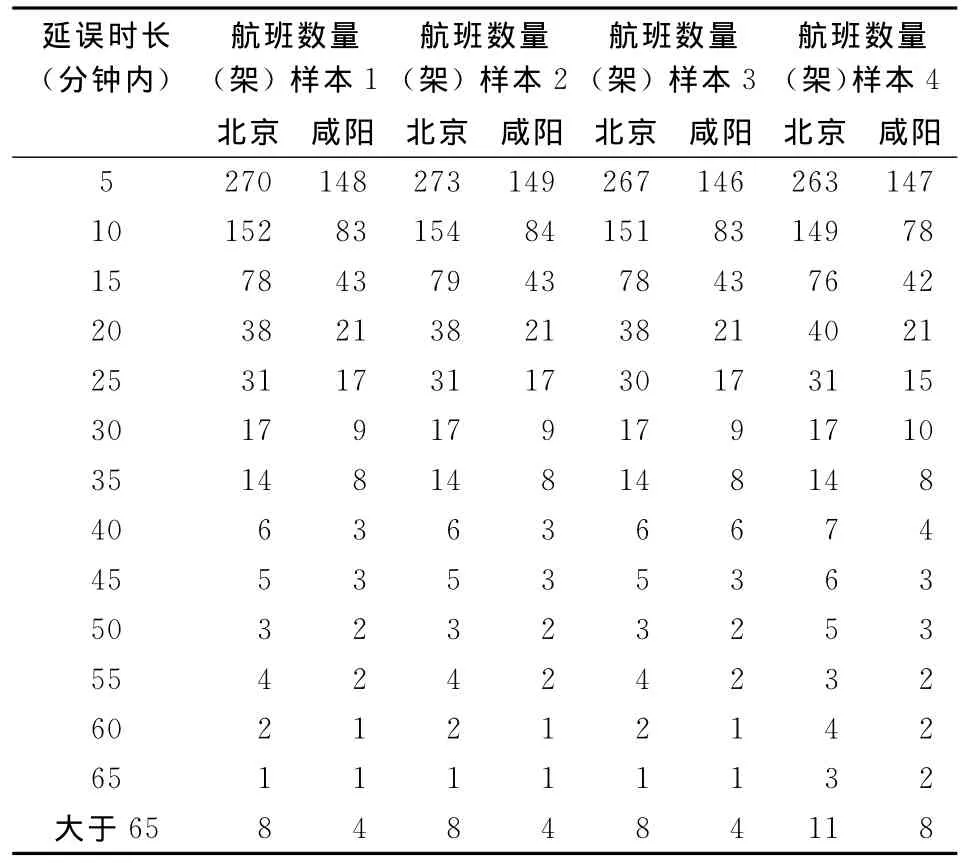
表2 北京首都机场和咸阳机场到达间隔统计表

表3检验结果表明，航班延误理论指数分布和实际分布的拟合程度超过98%，验证了航班到达和起飞符合泊松分布，航班延误符合指数分布，可以利用所统计的数据来建模。

西安咸阳机场和首都机场飞机到达泊松分布的系数分别为：

表3 航班延误实际分布与理论指数分布拟合度分析结果表

咸阳机场：1／λ＝到达间隔的平均时间＝3．6分钟；λ＝16．8（架次／小时）。

首都机场：1／λ＝到达间隔的平均时间＝1．9分钟；λ＝31．5（架次／小时）。

三、不同运行环节航班延误的排队模型

为了更好地应对和处理由天气、军事活动、流量控制和机械故障等不可控因素引起的航班延误，做好相应的延误服务补救，减少由旅客、机场和航空公司等可控因素引起的安检延误、起飞延误、到达延误以及由此引发的延误波及效应，可以基于指数分布验证结果，建立动态排队模型，进一步识别和剖析航班延误的各关键影响因素及其影响程度大小。

机场作为公共基础设施，一般实行超前设计建设，在相对较长的时间内，其跑道数量基本固定不变（服务台数不变），又因航班延误更多发生在大中型枢纽机场，其跑道数量基本为两个，因此这里分析统一采用双跑道模式。对于航班排队过程中的服务规则，遵守航空运输业的先到先服务规则。

一般排队模型用 A／B／C：a／b／c表示：A表示系统中排队对象的到达分布，如泊松分布、指数分布；B表示系统服务时间的分布，如指数分布；C表示服务台的个数；a表示服务规则，如先到先服务、后到先服务；b表示系统容量；c表示顾客来源的最大量［16］234－259。

航班的到达和起飞都服从泊松分布，航班到达和起飞服务时间服从指数分布。那么，无论对于安检、降落还是起飞排队，根据上面的分析，可得到如下的假设结论：

那么，安检、起飞和降落三个环节的排队模型如下。安检排队是一个典型的M／M／D模型，乘客到达服从泊松分布，每个乘客接受安检的时间服从负指数分布。

起飞排队和降落排队模型会因飞机起飞降落模式的不同而不同。当起飞和降落相分离，各自使用不同的专用跑道时，起飞和降落是两个相互独立的典型M／M／1／先到先服务模型；当起飞和降落共用一条跑道，按照“先到先服务”的顺序起飞或降落时，构成了一个2M／M／1／先到先服务模型系统；当起飞和降落采用先到先服务原则，混合排队使用两条跑道时，起飞和降落相互关联、相互影响，构成了一个2M／M／2／先到先服务模型系统。

本文分析基于国内大型机场，采用的是双跑道混合模式，其基本排队模式是2M／M／2模式。用λ1代表飞机起飞的泊松分布，用λ2代表飞机到达的泊松分布，用λ3表示乘客到达机场的泊松分布，用U1代表飞机起飞所用时间的负指数分布，用U2代表飞机降落所用时间的负指数分布，用U3代表乘客进行安检过程中所耗时间的负指数分布。

此时，排队模型相当于一个飞机来源服从（λ1＋λ2）的泊松分布；这里的服务时间仍然是U1和U2，因为每天进出一个机场的飞机数量基本相同，可选用（U1＋U2）／2作为服务时间所服从的指数分布；服务台数是双跑道——双服务台；排队规则是先到先服务。

四、航班延误的动态排队模型

将上面的三个可控延误模型以及航班延误波及模型汇合，建立总的可控制延误模型如图1所示。

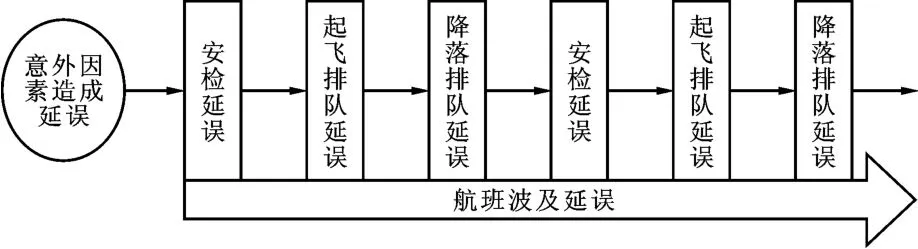
图1 可控因素引起的航班延误示意图

该模型仅考虑一次意外所造成的延误以及由此而产生的波及效应。假设在其它情况都正常时，由于一次意外的检修、天气等因素，造成在航班运行过程中的任何一个环节的初始延误及飞机某一排队的一个意外增加，接着会因航班延误的波及效应影响到飞机运行其它一系列环节。当不考虑由不可控因素引起的航班延误时，各个机场的延误相互独立，波及航班延误也不再是一个连续的过程，仅将安检、起飞、降落等各个阶段分别加入可控制延误模型。此时，各个环节的排队队长就是在原有正常队长的基础上加一个因波及延误而产生的波及队长。

已有文献证明，航班运行各个环节的波及延误效应基本呈现指数递减态势，且纵向传递近似于以1／2为等比的递减数列，因此可以假设航班延误的波及效应呈现平稳递减。假设缓冲时间为H，若延误时间小于H，则可被直接缓冲消除；若大于H，只会一部分被消除。

假设初始延误＝D0，每个阶段延误波及被缓冲消除该阶段延误的一半，则有：

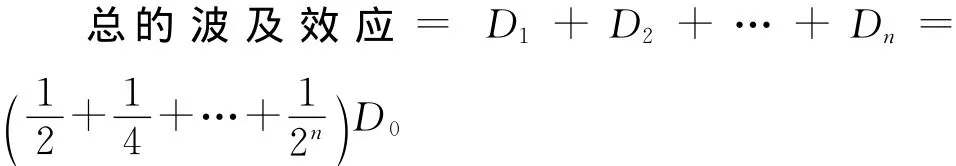
可控制延误模型各个环节的延误时间为：

在初始机场中：飞机起飞排队延误＝飞机排队队长＊平均服务时间＋延误时间

当考虑因天气、流量控制和军事活动等不可控因素时，这些因素引发的延误可能会发生在航班运行的各个环节，在此将以各因素近三年引发的航班延误的平均发生率把它们纳入模型，形成了航班延误的总动态排队模型（图2）。

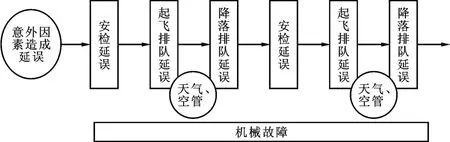
图2 加入不可控因素动态排队模型

根据最近三年航班延误影响因素的统计数据，流量控制、军事活动和天气引发的航班延误发生概率分别为0．25、0．09和0．21。

五、模型仿真模拟和结果分析

以咸阳机场为初始出发机场，基于西安—成都—云南—杭州—西安四个机场组成的航班运营闭环，利用2013年3月1日—6月30日该闭环中航班延误的数据，模拟仿真分析各个关键影响因素对于航班延误的影响程度（仿真模拟示意图见图3）［17］。

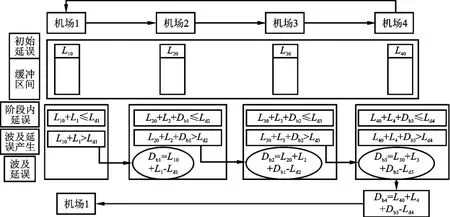
图3 仿真模拟分析示意图

模拟的假设前提有：（1）机场采用的是双跑道混合模式，因而无需对一个航班在机场中的到达和起飞单独进行分析，而将机场看作一个整体进行分析；（2）闭环中的每个机场具有相同的特质，它们的起飞和到达分布、服务能力都相同。虽然所选的四个机场特质有区别，但是运行模式、航班延误造成因素等大同小异，且它们都属于中型枢纽机场；（3）航班运行的闭环过程包含了所有影响航班延误的因素；（4）对于各个机场，设置一个正常排队队列L0和一个会导致航班延误的临界队长Ld，其中L0是指现有的机场服务能力水平下的正常期望队长；Ld是指在闭环的一个机场中，本阶段所能达到缓冲队长，在这个范围内，机场可以内化延误而不产生波及效应，否则产生波及效应［9－10］。

在上述假设基础上，利用matlab软件工具和设计模型对四个机场的各类数据进行模拟，结果见表4。依据表4结果绘制出由不同影响因素引发的航班延误发生频率及其影响程度图（图4），其中横轴表示各因素发生的频率高低，纵轴表示影响程度的强弱，椭圆形大小代表了此种因素对于航班延误的影响大小：椭圆面积越大，则影响越大；面积越小，影响越小。表5给出了各个影响因素对航班延误影响的大小和发生频率高低的排序。

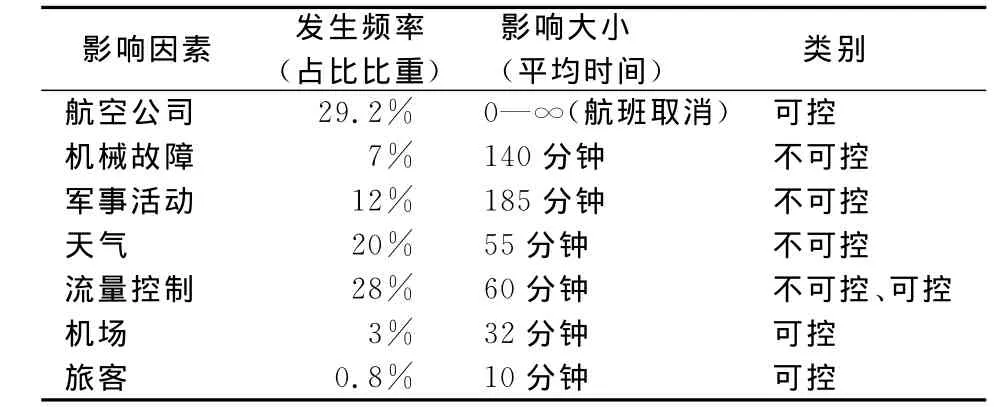
表4 各关键影响因素对航班延误影响大小仿真模拟结果表

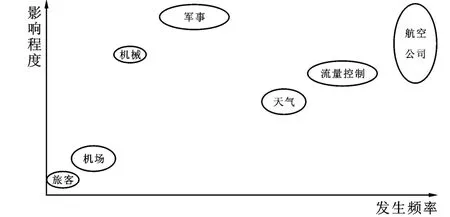
图4 各关键影响因素对航班延误影响大小仿真模拟结果示意图

表5 航班延误影响因素排序

表5和图4仿真模拟结果显示：（1）仿真结果与官方统计的各因素引发的航班延误占比历史数据排序相似，反映官方统计从历史数据角度较为准确地反映了各关键因素引发航班延误的频率，但各因素的影响程度和频率并不完全一一对应。这说明航班延误服务补救措施的制定，不能仅依据各影响因素的发生频率，还必须考虑其影响程度。（2）模拟结果表明，航空公司因素引发的航班延误不仅发生频率高，而且影响程度很大，为30%，延误时长往往不可预测。这进一步说明政府必须尽快制定统一和具有可操作性的航班延误服务补救制度，通过制度的设立激励约束航空公司通过航班计划的合理安排和运力的合理分配，积极应对减少航班延误。（3）流量控制和天气因素引发的航班延误频率高，分别为28%和20%，影响程度也大，延误平均时长分别为60分钟和55分钟。面对这两个因素引发的高频率延误，一方面是做好延误的服务补救，减少其震荡延误；另一方面是进行空域改革，提高空域容量。（4）值得关注的是军事活动和机械故障因素，它们引发的航班延误发生频率一般，分别为12%和7%，但以延误平均时长反映的影响程度很大，分别为185分钟和140分钟，位居第二、三位，远远超过了旅客的等待忍耐时限，是航班延误服务补救的重点和难点。（5）由机场和旅客因素引发的航班频率较低，影响程度也很低，但由航班延误引起的冲突经常发生在机场，旅客非理性行为成为航班延误新的增长点和社会的关注点，说明延误服务补救中，关注服务旅客始终是航空运输的核心。

六、结 论

本文基于航班运行流程，通过识别航班延误的原因及其主要发生的环节，对航班延误的泊松分布进行了验证，构建了航班延误的一般和动态排队模型，并运用样本机场的数据，对动态模型进行了模拟分析，得到以下结论：

航班运行流程闭环的不同阶段分解分析反映，航班延误的主要原因包括流量控制、军事活动、天气等不可控因素和安检、旅客、飞机起飞降落排队、机械故障、机场原因等可控因素。

数理推导和实证分析证明，飞机的起飞和到达都服从泊松分布，航班延误符合指数分布，咸阳机场和首都机场的飞机到达泊松分布的系数分别为16．8（架次／小时）和31．5（架次／小时）。

依据航班运行流程，基于指数分布验证结果，将不可控延误因素作为既定背景假设，构建了可控航班延误发生较高的安检、起飞和降落三个环节的动态排队模型，以识别和剖析航班延误的各个主要影响因素，指出安检排队是一个典型的M／M／D模型。机场的起飞降落有三种模式：分离式下的起飞和降落系统是两条相互独立的典型 M／M／1／先到先服务模型系统；单跑道混合式下的起飞和降落共用一条跑道，按照“先到先服务”的顺序起飞或降落，构成了一个2M／M／1先到先服务模型系统；中国现阶段大型机场比较通用的是双跑道混合式，飞机起飞和降落实行混合排队，先到先服务，两个环节相互关联、相互影响，构成了一个2M／M／2先到先服务模型系统。因为航班延误主要发生在大型繁忙机场，2M／M／2模型就成为航班延误关键影响因素发生频率及影响大小识别的基准模型。

按照对延误主要影响因素分析识别的结果以及各因素历史统计发生频率，将各关键因素及航班延误的波及延误加入基准模型，构建了航班延误的动态排队模型，模拟仿真分析在西安—成都—云南—杭州—西安四个机场组成的闭环中航班延误的各个影响因素对于航班延误的影响程度，结果证明各因素引发的航班延误频率高低和其影响程度并非完全一一对应。在识别的七个主要影响因素中，航空公司因素发生频率最高、影响最大；流量控制因素排名第二，发生频率较高、影响大；天气因素发生频率较高、影响较大；军事活动发生频率一般，但影响大；机械故障频率较低、影响较大；机场因素频率较低、影响较小。

［1］ 数字之道．航班延误，谁会“赔你等”［EB／OL］．［2013－07－30］．http：／／news．sohu．com／s2013／hangbanyanwu／2013－07－18．

［2］ 杨秀云，王全良，何建宝．航班延误问题的研究动态、演化趋势和启示［J］．经济经纬，2013（4）．

［3］ Allan S S，Beesley J A，Evans J E，et al．Analysis of Delay Causality at Newark International Airport［C］．4th USA／Europe Air Traffic Management R＆D Seminar，New Mexico，2001．

［4］ 张静．天气影响的机场容量与延误评估研究［D］．南京：南京航空航天大学博士学位论文，2012．

［5］ Abdelghany K F，Shah S S，Raina S，et al．A Model for Projecting Flight Delays during Irregular Operation Conditions［J］．Journal of Air Transport Management，2004，10（6）．

［6］ 邵维亮．基于航班运行仿真的航班延误水平评价［D］．广汉：中国民航飞行学院硕士学位论文，2012．

［7］ Jarrah A I Z，Yu G，Krishnamurthy N，et al．A Decision Support Framework for Airline Flight Cancellations and Delays［J］．Transportation Science，1993，27（3）．

［8］ Liou J S．Delay Prediction Models for Departure Flights［C］．Transportation Research Board 85th Annual Meeting，Washington，2006．

［9］ Georgina Santos，Maёl Robin．Determinants of Delays at European Airports［J］．Transportation Research Part B：Methodological，2010，44（3）．

［10］邢有洪，李晓津，金永利．航班延误影响因素的实证分析［J］．会计之友，2010（8）．

［11］邵荃，罗雄，吴抗抗，等．基于贝叶斯网络的机场航班延误因素分析［J］．科学技术与工程，2012（10）．

［12］Lubbe B，Victor C．Flight Delays：Towards Measuring the Cost to Corporations［J］．Journal of Air Transport Management，2012，19（1）．

［13］Daniel J．Congestion Pricing and Capacity of Large Hub Airports：A Bottleneck Model with Stochastic Queues［J］．Econometrica，1995，63（2）．

［14］Glockner．A Dynamic Stochastic Model for the Single Airport Ground Holding Problem ［J］．Transportion Science，1993，41（4）．

［15］唐应辉．排队论：基础与分析技术［M］．北京：科学出版社，2006．

［16］华兴．排队论与随机服务系统［M］．上海：上海翻译出版公司，2007．

［17］姚韵，朱金福．基于可拓关联函数的不正常航班管理预警模型［J］．西南交通大学学报，2008，43（1）．

The Identification of Flight Delays＇Determinants and Their Impact Degree：Based on the Analysis of Dynamic Queues Model

YANG Xiu-yun1，WANG Jun1，2，HE Jian-bao1
（1．School of Economics and Finance，Xi＇an Jiaotong University，Xi＇an 710061，China；2．Higher Vocational Technical College，Xi＇an University of Finance and Economics，Xi＇an 710061，China）

This paper analyzes the different stages of flight operation process loop，and identify the determinants of flight delays including flow control，military activity，weather and other uncontrollable factors，security，passenger，aircraft take-off and landing queue，mechanical failure，airports and other controllable factors．Mathematical and empirical analyses verify the aircraft＇s take-off and landing are Poisson distribution，flight delay is exponential distribution．This paper constructs a dynamic queuing model which contains different aspects delay and delay spread．The simulation analysis of dynamic queuing model with typical airport delay data points out that the frequency and impact degree of flight delays caused by different determinants are not entirely correspond．Airlines factor with the highest frequency and the most influential impact；flow control with higher frequency and high impact；but weather factors for the higher frequency and greater impact；military activities in a general frequency but the greatest impact；mechanical failure with lower frequency but greater impact；airport factor for lower frequencies and less influence

flight delay；Poisson distribution；exponential distribution；queuing model

F560．6∶F224．34

A

1007－3116（2014）04－0088－08

2013－12－02

教育部人文社会科学规划项目《我国航班延误的决定因素及治理补救机制研究》（11YJA790183）；教育部新世纪优秀人才支持计划《航班延误的服务补救质量动态优化研究》（NCET120459）

杨秀云，女，陕西澄城人，经济学博士，教授，博士生导师，研究方向：产业经济与公司战略；

王 军，男，陕西蒲城人，博士生，副研究员，研究方向：产业经济；

何建宝，男，陕西汉中人，硕士生，研究方向：产业经济。

（责任编辑：崔国平）