内压作用下圆柱壳开孔接管区的力学分析

杜四宏，周帅彪

(中国核电工程有限公司郑州分公司，河南 郑州 450052)

设备与自控

内压作用下圆柱壳开孔接管区的力学分析

杜四宏，周帅彪

(中国核电工程有限公司郑州分公司，河南 郑州 450052)

应用Ansys对内压作用下圆柱壳开孔接管区进行了有限元应力分析，得到了其受力特性和应力分布规律，并对其进行了应力强度评定。

压力容器；圆柱壳；接管；强度评定

压力容器是石油化工、轻工、电厂、化学化工、制药等工业生产中广泛使用的设备，由于各种工艺和结构上的要求，常常需要在压力容器上开孔并安装接管[1]。由于几何形状及尺寸的突变，受内压壳体与接管连接处附近的局部范围内会产生较高的不连续应力，引起开孔附近区域应力集中，在容器上造成局部高应力，从而影响容器的整体承载能力，该部位很有可能成为设备的破坏源，因此对开孔接管部位作详细的应力分析和强度评定是确保压力容器安全运行必不可少的内容。

容器开孔接管区的应力状况非常复杂，这是因为开孔破坏了壳体材料的连续性，削弱了原有的承载面积，另外，在开孔边缘附近必定会造成应力集中，接管的存在使开孔接管区成为总体结构不连续区，壳体与接管在内压作用下自由变形不一致，在变形协调过程中将产生边缘应力。同时，接管与壳体是通过焊接连接在一起的，焊缝的结构尺寸如焊缝高度、过渡圆角等会形成局部结构不连续，形成局部不连续应力。因此，对这类应力的求解是相当复杂的，工程上常采用应力集中系数法、数值解法、实验测试法和经验公式来计算局部应力[2]。应力数值计算的方法比较多，如差分法、变分法、有限单元法和边界元法等。近年来，在计算机技术和数值分析方法的支持下发展起来的有限元分析（FEA, Finite Element Analysis）方法则为解决复杂的工程分析计算问题提供了有效的途径。有限单元法的基本思路是将连续体离散为有限个单元的组合体，以单元节点的参量为基本未知量，单元内的相应参量用单元节点上的数值插值，将一个连续体的无限自由度问题变成为有限自由度的问题，再利用整体分析求出未知量。显然，随着单元数量的增加，解的近似程度将不断改进，如单元满足收敛要求，近似解也最终收敛于精确解。ANSYS软件是集结构、流体、电场、磁场和声场分析为一体的大型通用有限元分析软件[3]，拥有丰富和完善的单元库、材料模型库和求解器，在合理的边界条件下可获得问题的精确求解。

为了揭示受内压作用下圆柱壳容器开孔接管区的受力特性和应力分布规律，本文对某压力容器开孔接管区进行了有限单元法分析并对其进行了应力强度评定。

1 模型的有限元分析

1.1 问题描述

圆柱壳压力容器的筒体外径Do=2060mm，筒体壁厚tc=30mm，开孔接管的外径do=530mm，壁厚tn=15mm，该压力容器与接管的材料均为16MnR。接管的内伸长度li=195mm，容器与接管的外侧过渡圆角r1=30mm，内侧过渡圆角r2=15mm；压力容器筒体内压P=1.2MPa。材料的弹性模量E=2.0×105MPa，泊松比μ=0.3。圆柱壳开孔接管的几何尺寸如图1所示。

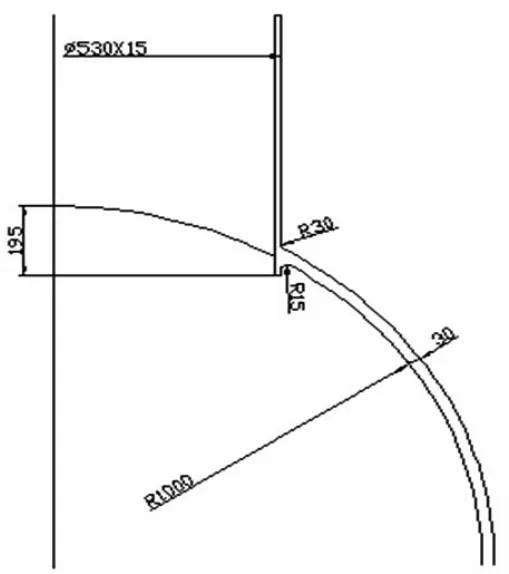
图1 筒体结构简图

1.2 几何模型

不同结构组合壳，在结构边缘处，有不同的边缘应力，有的边缘效应显著，其应力可达到很大的数值，但它们都有一个共同特性，即影响范围很小，这些应力只存在于连接处附近的局部区域。受边缘力和力矩作用的圆柱壳，由式 （1）计算：

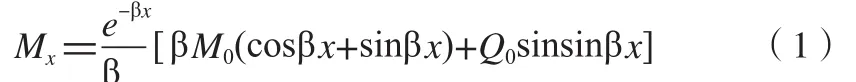
式中：x为所考虑点离圆柱壳边缘的距离；

β为因次为[长度]-1的系数，；

Mx为单位圆周长度上的轴向弯矩；

M0为边缘力矩，单位圆周长度上的轴向弯矩当x=0时的边界条件；

Qx为单位圆周长度上的横向剪力；

Q0为边缘力，单位圆周长度上的横向剪力当x=0时的边界条件。

可知，随着离边缘距离x的增加，各内力呈指数函数迅速衰减以至消失，这种性质称为不连续应力的局部性。当时，圆柱壳中产生的纵向弯矩的绝对值为：

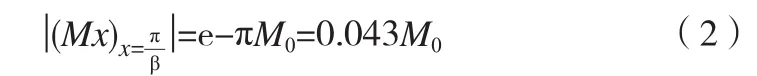
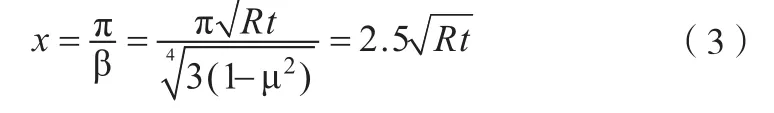
筒体长度及接管外伸长度应远远大于各自的边缘应力衰减长度，因此，取圆柱壳的长度L=4000mm，接管的外伸长度l=500mm。由于仅考虑内压作用下圆柱壳接管处的应力状况，为此几何模型可利用结构的对称性（模型在结构上是对称的，同时载荷也是对称的）取开孔接管区的1/4建模，模型如图2所示。

1.3 网格划分

采用SOLID45单元对几何模型进行离散化，此模型共划分了7668个 节点，5720个单元。离散化之后的单元网格如图3所示。

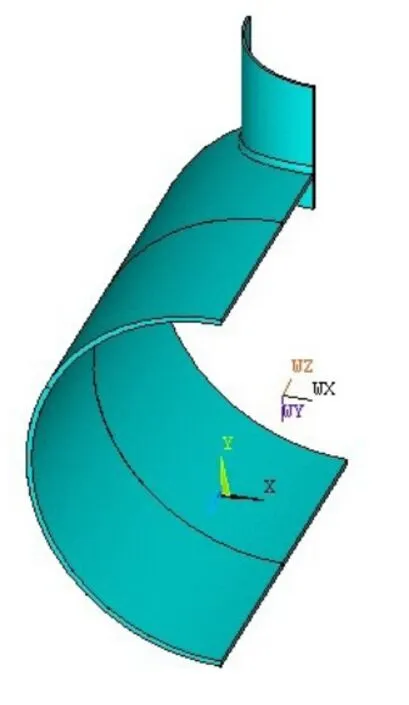
图2 几何模型

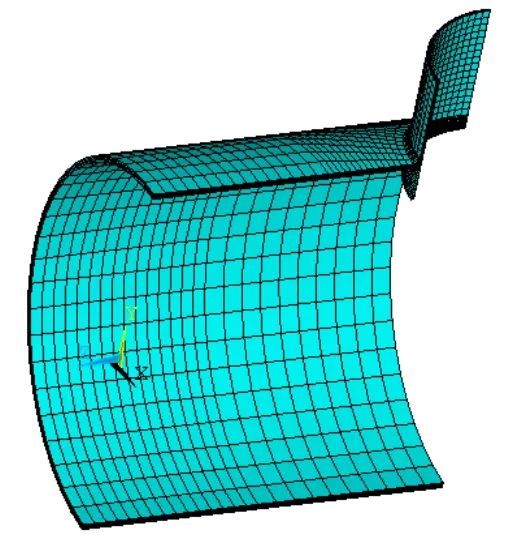
图3 单元网格

1.4 边界条件

由于结构是轴对称的，载荷也是轴对称的，因此可将模型简化为轴对称问题。其对称面施加对称约束，接管端部约束轴向位移，施加完约束条件的有限元模型如图4所示。圆柱壳内表面和接管内表面承受内压P，接管内伸部分的外表面也承受内压P，筒体端面施加轴向平衡面载荷Pc，并按公式（4）进行计算：

经计算得：Pc=19.7MPa。

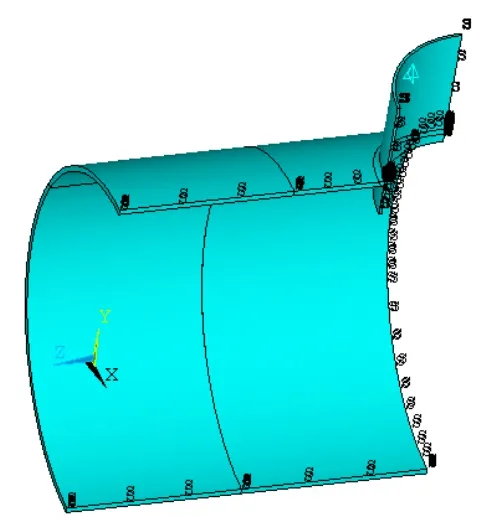
图4 有限元计算模型

2 计算结果及强度评定

圆柱壳开孔接管区的应力强度云图如图5所示。可见最大应力发生在圆柱壳与接管的连接区。《JB 4732—1995钢制压力容器——分析设计标准》[4]要求对计算部分的应力作详细的计算，按应力的性质、影响范围及分布状况将应力分类为一次应力、二次应力和峰值应力，对于不同性质的应力给予不同的限制条件。

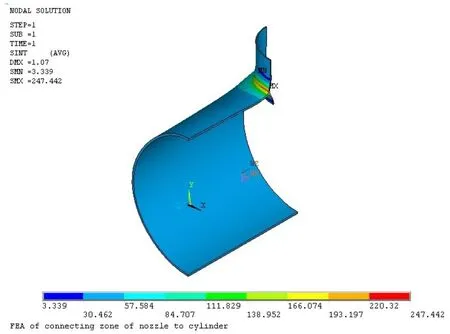
图5 应力强度云图

应力强度的评定方法可分为点处理法和线处理法，对于复杂结构还可以采用面处理法[5]。本文采用线处理法，即将危险截面上各应力分量沿应力分布线进行均匀化和线性化处理，并得到沿应力分布线的平均应力（薄膜应力）、线性应力（弯曲应力）和应力的非线性部分，再根据应力对容器失效所起作用的大小分为一次总体薄膜应力、一次局部薄膜应力、一次弯曲应力和峰值应力，并计算出不同应力类型及其组合的应力强度，要求相应的应力强度不超过各自的许用值[6]。各应力强度的限制条件如下：

1）一次总体薄膜应力强度Pm：Pm≤1.0 Smt=143.5

2） 一次局部薄膜应力强度Pl：Pl≤1.5Smt=1.5× 143.5=215.25 MPa

3）一次薄膜应力+一次弯曲应力强度Pm+Pb：Pm+Pb≤1.5Sm

t=1.5×143.5=215.25 MPa

4）一次+二次应力强度Pm+Q：SⅣ≤3Smt=3× 143.5=430.5 MPa

5）峰值应力强度：SⅤ≤2Sa=2×138=276 MPa

根据应力处理线的划定原则，针对圆柱壳接管连接区在应力强度最大处划出一条应力处理线，如图6所示（图中虚线为结构受内压前的形状，实线为受内压后的形状）。从表1中的数据可知，圆柱壳接管连接区域能满足强度要求。

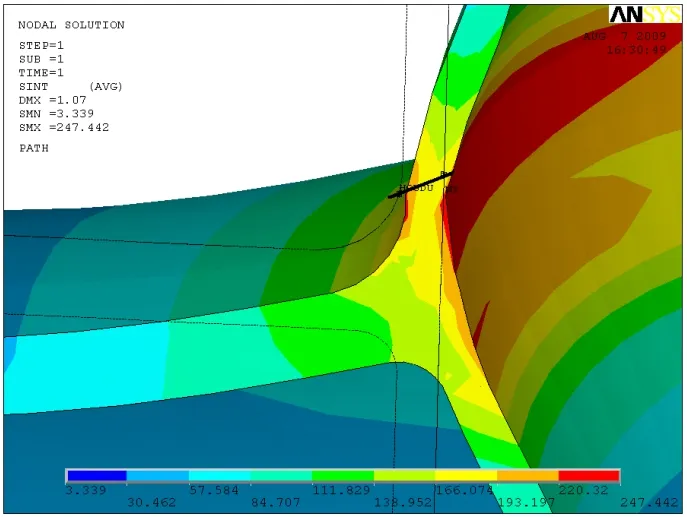
图6 线性化路径

表1 应力处理线评定结果

3 结论

经过对该结构的力学分析，圆柱壳接管区域在给定的操作工况及尺寸条件下，强度满足相应要求。

圆柱壳与接管连接的区域是容器中应力高强度区，也是容器最容易出现破坏的地方，因此在设计、制造过程中应保证该处的尺寸。另外，几何形状或尺寸的突然改变是产生应力集中的主要原因之一，因此，在圆柱壳与接管连接处应尽量采用圆弧或经形状优化的特殊曲线过渡以减少该处的应力。

[1] 温洁明，等.压力容器开孔接管区的有限元分析和实验研究[J].装备制造技术，2006(4)：27.

[2] 郑津洋，董其伍，桑芝富.过程设备设计[M].北京：化学工业出版社，2001.

[3] 王富耻，张朝辉. ANSYS10.0有限元分析理论与工程应用[M].北京：电子工业出版社，2006.

[4] JB 4732-1995，钢制压力容器——分析设计标准[S].

[5] 贺匡国.压力容器分析设计基础[M].北京：机械工业出版社，1995.

[6] 郑津洋，等.基于整体有限元应力分析的齿啮式快开压力容器设计[J].压力容器，2003，20(7)：22.

Mechanical Analysis of Cylindrical Pressure Vessel with Normally Intersecting Nozzle

DU Si-hong, ZHOU Shuai-biao
(China Nuclear Power Engineering Co. Ltd., Zhengzhou Branch, Zhengzhou 450052, China)

To cylindrical pressure vessel with normally intersecting nozzle, finite element analysis was used on the basis of Ansys, drawing its stress characteristics. With regard to dangerous section, the strength assessment was carried out.

pressure vessel; cylindrical shells; opening tubing connection; strength assessment

TH 49

B

1671-9905(2014)08-0060-03

杜四宏，男，工程师，河南省郑州市中原东路96号中国核电工程有限公司郑州分公司，主要从事力学计算和有限元分析，13693712947

2014-07-07