杠杆应该向哪端下沉
成联国
(昆明市官渡区第六中学,云南 昆明 650217)
在最新义务教育教科书2012版的沪科版8年级物理“科学探究 杠杆的平衡条件”的习题中有这样一道题(课本第190页第6题):
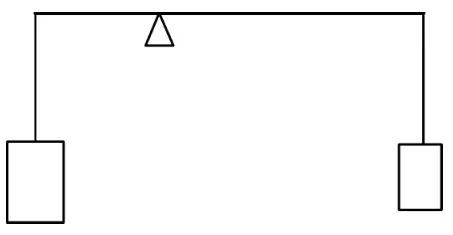
图1
一根杠杆两端分别挂着质量不相等的两铁块,如图1所示,此时杠杆静止.若将两铁块同时浸没于水中,杠杆是否依然平衡?若不平衡,哪端下沉?
很多学生认为应该向右边下沉.因为杠杆的左右两边都是铁块,密度相同,且左边的铁块的质量M1明显大于右边的质量M2,左边铁块的体积V1大于右边的体积V2(即V1>V2),左边铁块受到的浮力F1′大于右边铁块受到的浮力F2′,因此应向右边倾斜,右端下沉.
一些教材解读类参考书中,给出的习题解答是“杠杆不再平衡,右端下沉”,解析和上面学生的说法基本一致,甚至某出版社的“‘十二五’重点课题高效课堂研究成果”的教案与作业设计书,也是给出这样的答案.很多教师稍有疏忽也这样讲解,也就不足为奇了.但是真是这样的吗?
杠杆应向哪端倾斜,主要是看哪端的力和力臂的乘积大,即力矩大,就向哪端倾斜并下沉.
为了简化题目,我们认为杠杆是在水平位置平衡,如图2.这样支点到左端末的长度L1即为左边物体通过细绳的作用力F1的力臂,支点到右端末的长度L2即为右边物体通过细绳的作用力F2的力臂.

图2
1 杠杆两端挂的是同种物质,浸没在水中
当杠杆水平位置平衡,且不考虑质地均匀的杠杆的质量时,左边的铁块受到重力G1和绳子拉力F1的作用而静止,如图3.因此F1=G1=ρgV1,同理右边铁块也有F2=G2=ρgV2.则根据杠杆平衡原理有F1xL1=F2xL2,可得
ρgV1L1=ρgV2L2,所以有V1L1=V2L2.
当把静止的杠杆上的铁块浸没入水中后,如图4.杠杆左右两边的铁块都受到的水对他们的浮力F1′和F2′.此时
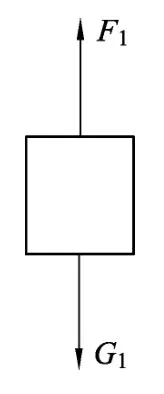
图3

图4
杠杆左右两端的作用力分别是F1-F1′和F2-F2′,而F1=ρgV1,F2=ρgV2,F1′=ρ水gV1,F2′=ρ水gV2,所以杠杆左端的力矩为M1=(F1-F1′)L1=(ρgV1-ρ水gV1)L1=(ρ-ρ水)gV1L1.杠杆右端的力矩为M2=(F2-F2′)L2=(ρgV2-ρ水gV2)L2=(ρ-ρ水)gV2L2.
通过比较,浸没后杠杆左右两端的力矩M1=M2,即(F1-F1′)L1=(F2-F2′)L2.所以杠杆依然处于平衡状态.那是不是题目中要考虑质地均匀的杠杆的质量呢?
假设杠杆左右两端的所受的重力分别为G1和G2,在空气中静止时,由杠杆的平衡条件有
当把静止的杠杆浸没入水中后,杠杆的左右两端的力矩分别为
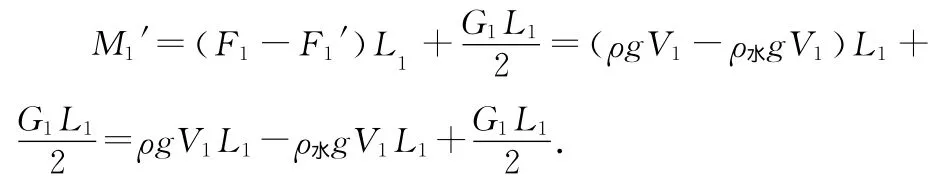
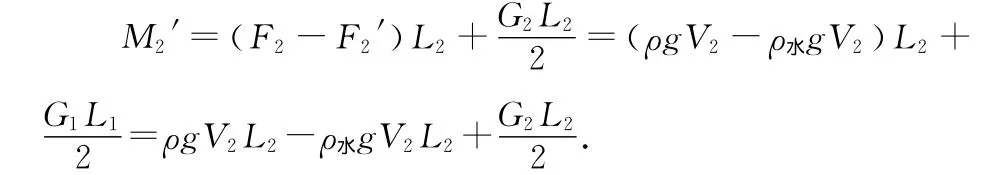
所以杠杆左右两端的力矩之差为

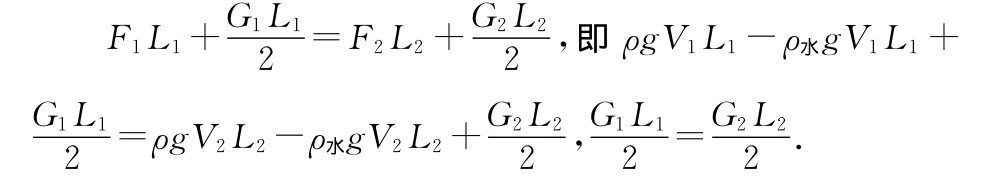
假设杠杆单位长度的密度为ρ0,则杠杆成为等臂杠杆,杠杆两端的铁块质量相等杠杆才能在空气中平衡.不符合题意.因此不存在.
而又无法比较V2L2-V1L1>0,还是V2L2-V1L1<0.因此无法断M1′-M2′=ρ水g(V2L2-V1L1)大于0还是小于0,所以杠杆不再平衡,但无法判断向哪端倾斜,哪端下沉.
很明显题目中是不需要考虑质地均匀的杠杆的质量的,而且这是针对8年级学生的习题.
归纳:当杠杆两端挂的是同种物质时,浸没在水中后,杠杆依然平衡.
2 杠杆两端挂的不是同种物质,浸没在水中
2.1 杠杆两端挂的是质量相同的不同种物质
例如:杠杆左右两端分别挂有质量相等的铁块和铝块,在空气中杠杆平衡,若将铁块和铝块同时浸没在水中,则杠杆
(A)不平衡,铁块一端下沉.
(B)不平衡,铝块一端下沉.
(C)平衡.
(D)无法判断.
解析:由于铁块和铝块的质量相同,杠杆在空气平衡时,杠杆是等臂杠杆L1=L2=L.而铁的密度大于铝的密度,即ρ铁>ρ铝,所以铁块的体积V铁小于铝块的体积V铝,即V铁<V铝.铁块受到的浮力F1′就小于铝块的浮力F2′.所以(G-F1′)L1>(G-F2′)L2,杠杆不再平衡,应该向铁块那一端倾斜并下沉.故选择(A).
2.2 杠杆两端挂的是体积相同的不同种物质
例如:杠杆左右两端分别挂有体积相等的铁块和铝块,在空气中杠杆平衡,若将铁块和铝块同时浸没在水中,则杠杆
(A)不平衡,铁块一端下沉.
(B)不平衡,铝块一端下沉.
(C)平衡.
(D)无法判断.
解析:由于铁块和铝块的体积V相同,铁的密度大于铝的密度,即ρ铁>ρ铝,所以铁块质量大于铝块质量,即m铁>m铝,相应的有G铁>G铝.又根据杠杆平衡原理G铁L1=G铝L2,因此铁块一端力臂小于铝块那一端的力臂,L1<L2.当铁块和铝块浸没入水中后,铁块和铝块体积相同受到水的浮力相等,F1′=F2′.由于F1′L1<F2′L2,G铁L1-F1′L1>G铝L2-F2′L2.所以杠杆不再平衡,应向铁块那一端倾斜、下沉.故选择(A).
归纳:当杠杆两端挂的是不同种物质时,浸没在水中后,杠杆不再平衡,杠杆向密度大的那一端倾斜并下沉.
3 杠杆两端挂的物体的密度小于液体的密度
杠杆两端悬挂的物体的密度小于液体的密度时,杠杆在空气中平衡,将物体放入液体中后,物体受到液体的浮力等于物体的重力,细绳对杠杆拉力为0.则有:(1)当不考虑质地均匀的杠杆质量时,杠杆依然平衡;(2)当考虑质地均匀的杠杆质量时,杠杆向力臂长的那一端倾斜,并下沉.
因此,以下所有讨论中物体的密度(包括等效后的密度)都大于液体的密度.
4 杠杆两端挂上物体后的特殊情况
(1)杠杆两端所挂的物体是空心物体,或有一个是空心物体.
以上问题讨论都是建立在不考虑杠杆的质量,杠杆两端所挂的物体是实心物体,且物体的密度大于液体的密度.如果杠杆两端挂的不是实心物体情况又会怎样呢?受影响于空心部分体积大小,但主要取决物体的总体积和质量,经等效后物体的平均密度(即物体的质量与总体积的比值).
①若等效后左右两端的平均密度相同,则物体浸没于液体中后,杠杆依然平衡;②若等效后左右两端的平均密度不同,则物体浸没于液体中后,杠杆向密度大的一端倾斜,并下沉.
(2)杠杆在让两端物体的下底面处在同一水平面上,实心物体从接触水面到完全浸没于水的过程中,杠杆应向哪端倾斜呢?与物体形状和质量分布有着重大关系,情况也较为复杂,因此不再讨论.
5 质地均匀的轻质杠杆,两端挂上不同的物质在空气中平衡后放入同种液体中
质地均匀的轻质杠杆(不考虑杠杆的质量),两端挂上密度为ρ1和ρ2的物体在空气中平衡,如图5.当把物体浸在密度为ρ液液体中,若该物为实心物体,密度ρ1和ρ2为两物体的密度,若物为空心物体或有空心物体,密度ρ1和ρ2为两物体的等效后的平均密度.情况又会怎样呢?

图5
当杠杆在空气平衡,很容易得到G1L1=G2L2,即ρ1gV1L1=ρ2gV2L2.
当杠杆浸没在水中,左右两边的物体都受到水的浮力F浮=ρgV.此时杠杆左端的力矩M1=ρ1gV1L1-ρ液gV1L1,杠杆右端的力矩M2=ρ2gV2L2-ρ液gV2L2.
杠杆左右两端的力矩之差为M1-M2=(ρ1gV1L1-ρ液gV1L1)-(ρ2gV2L2-ρ液gV2L2)=ρ液g(V2L2-V1L1).
(1)当ρ1=ρ2>ρ液时,由ρ1gV1L1=ρ2gV2L2,得V1L1=V2L2所以M1=M2,杠杆依然平衡;
(2)当ρ1>ρ2>ρ液时,由ρ1gV1L1=ρ2gV2L2,得V1L1<V2L2,所以M1>M2,杠杆不再平衡,杠杆向左端倾斜,即向物体密度大的一端倾斜;
(3)当ρ液<ρ1<ρ2时,由ρ1gV1L1=ρ2gV2L2,得V1L1>V2L2,所以M1<M2,杠杆不再平衡,杠杆向右端倾斜,即向物体密度大的一端倾斜.
综上论述,质地均匀的轻质杠杆两端挂上不同的物体在空气中平衡,浸在同种液体中后,杠杆是否再平衡,主要是讨论两端物体的密度(包括等效后的平均密度):①杠杆左右两端密度相同物体,浸没在同种液体中后,杠杆依然平衡;②杠杆左右两端密度不相同物体,浸没在同种液体中后,杠杆不再平衡,杠杆向密度大的一端倾斜,并下沉.
6 质地均匀的轻质杠杆,两端挂上不同的物质,放入密度不同的液体中

图6
质地均匀的轻质杠杆(不考虑杠杆的质量),两端挂上密度为ρ1和ρ2的物体在空气中平衡,如图6.当把物体浸没在密度为ρ3和ρ4液体中,若物体为实心物体,密度ρ1和ρ2为两物体的密度,若物体为空心物体或有空心物体,密度ρ1和ρ2为两物体的等效后的平均密度.情况又会怎样呢?
当杠杆在空气中平衡时有ρ1gV1L1=ρ2gV2L2=M0(M0>0).
当把杠杆放入密度分为ρ3和ρ4液体中后,杠杆左端的力矩为M1=ρ1gV1L1-ρ3gV1L1.杠杆右端的力矩为M2=ρ2gV2L2-ρ4gV2L2.
则杠杆左右两端的力矩之差为
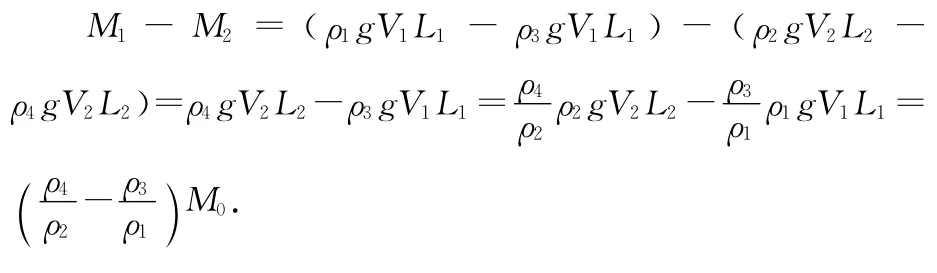
(1)当M1=M2时物体密度与液体密度的比值相等时,杠杆依然平衡;
(2)当M1>M2时杠杆不再平衡,向杠杆左端倾斜并下沉,即杠杆向物体密度与液体密度比值大的一端倾斜并下沉;
(3)当M1<M2时,杠杆不再平衡,向杠杆右端倾斜并下沉,即杠杆向物体密度与液体密度比值大的一端倾斜并下沉.
综上论述,质地均匀的轻质杠杆,两端挂上密度不同的物体在空气中平衡,浸在密度不同的液体中后,杠杆是否再平衡,主要是讨论两端物体密度(包括等效后的平均密度)与液体密度的比值,即密度比:①密度比相等时,杠杆依然平衡;②密度比不相等时,杠杆不再平衡,杠杆向密度比大的一端倾斜,并下沉.
我们在讨论杠杆的平衡问题时,杠杆平衡是因左右两端力和力臂的乘积(即力矩)相等;杠杆不平衡,杠杆应向哪端倾斜,主要是看哪端的力和力臂的乘积大,即力矩大,就向哪端倾斜并下沉.物体浸没在液体中后,原来是比较繁难杠杆平衡问题,反而可以简化为比较杠杆左右两端物体密度和液体密度的比值,即密度比,于是就轻而易举地解决问题了.

