一图抵千言——图像在高中物理教学中的作用例析
徐海菊
(江苏省南通中学,江苏 南通 226001)
中学阶段的物理学习离不开图像,平时学习中接触到的图像素材有图片、示意图、曲线图、函数图像等.识图、析图、画图是学生提高物理学习效果的一种重要手段,高中阶段,学生的抽象思维占物理学习思维的主体地位,由于学生的抽象思维还不够成熟,因此需要形象思维的激发,简洁、形象的示意图能够让学生切入到物理事件的轮廓、轨迹、原理,进而加深对概念和规律的理解;函数图像、轨迹图等则能够引导学生去发现物理规律内在结构以及结构中各物理量对应的变化关系,能够更为清晰、直观地展示物理情景的动态过程.可以说“一图抵千言”,图像在物理学习中的作用是不可替代的.
1 图像用于概念教学,无形“画”为有形
清晰、准确的理解并建立物理概念是学生高中阶段学好物理的基础,教育学、心理学研究表明,接触并记住概念的定义不等同于知识的内化,要想使物理概念在头脑中生根需要大量直观的认识作为基础,而且要经历一个“实物直观→模型直观→图形直观→语言直观”的渐进式发展过程,在提供直观认知时充分利用图像,能够促使抽象概念形象化.
例如,“力”这个概念,引入了力的图示和力的示意图之后,让学生在理解“力是物体间的相互作用”这个概念的基础上,对力的本质有了更深入的理解,同时“力”也因此变得形象化,可操作化了.再例如,电场这一章节的几个概念,在引入了电场线、磁感线、等势面等图像化的概念后,一系列概念的理解就更容易了.
2 图像用于规律教学,难“画”为易
首先,借助于示意图可以使物理规律及物理过程跃然“图”上,这个形象化的过程促进了学生思维的发展,提高了学生抽象概括的能力.
例如,“牛顿第一定律”的教学,将伽利略理想斜面实验示意图画在黑板上(如图1所示),或是将示意图投影出来,能够有效消除学生的生活经验对规律的干扰,深化对规律的理解.

图1
其次,函数图像可以揭示物理规律的本质,尤其是具有对比性的图像,能够让学生加深对物理规律本质的认识,便于物理规律的内化.
例如,“自由落体运动”和“竖直上抛运动”不仅是匀变速直线运动的两个特例,而且它们也是重要的运动模型,但想让刚进入高中不久的学生深入理解其中的动力学特点和所蕴含的物理规律,却不仅仅是靠教师多讲、学生多练可以实现的.借助于数学函数图像(如图2所示),可以有效缩短学生的思维进程,学生对竖直上抛运动的规律及对称性理解更为透彻.
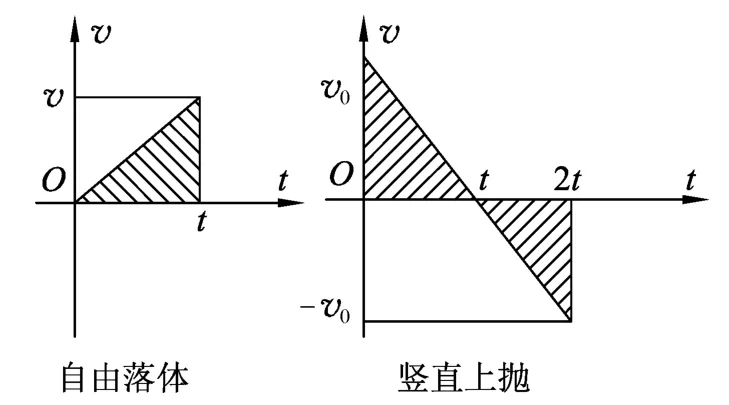
图2

图3
再如,研究“电源输出功率随外电阻变化的规律”时,如果采用理论推导,对于公式必须对公式再变形,运用数学基本不等式才可以判断,而且对于特定的电路,在动态分析的过程中,外电阻的阻值一般调不到与电源内阻的阻值相等,学生对此规律的认识表现为无所适从.如果将公式与图像(如图3所示)结合起来引导学生去分析的话,学生能够很直观地从整体上把握规律,加深思维痕迹.
3 图像用于实验教学,千言“画”为一图
实验教学是高中物理教学的一个重要内容,实验教学重在“探究”,每节实验课都有明确的实验目的,要求学生利用原有认知进行方案的设计,选择合适的装置进行操作,实验过程中记录和处理数据.图像在实验教学尤其是在数据处理中起到的作用是不可忽视的.
(1)借助图像简化数据处理,直观揭示物理本质和规律.
例如,在探究“加速度与质量的关系”时,保持小车所受的合力不变,得到小车的加速度与质量的几组数据,学生很难直接看出两者间的相互关系,此时先引导学生描点连图,作出a-m函数图像,图像看上去好像是一条双曲线(如图4所示),继而猜测出小车的加速度a与小车的质量m成反比.为了进一步验证猜想,可以再引导学生变换坐标轴对应的物理量,作出图像,此时可以得到一条过原点的直线(如图5所示),学生由图像很容易得出结论:当合力一定时,小车的加速度与质量成反比.

图4
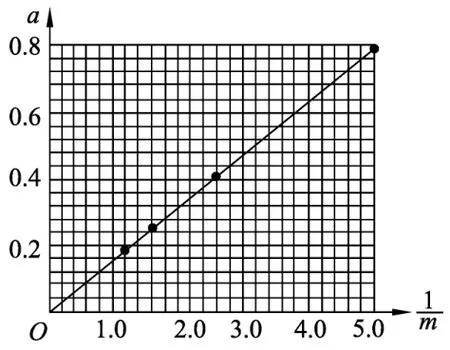
图5
(2)借助函数图像,实施间接测量.
对于物理中的函数图像,学生不仅要理解图像上的坐标所对应的物理量的意义,还要掌握图像的斜率、截距、面积等信息赋予的特定的物理意义.
例如,在“测定电源的电动势和内阻”的实验中,根据实验测量的数据描点连图,图像为如图6所示中的实线.这时,教师应引导学生将实线两端向外延伸(图6中虚线),交两坐标轴于Im、Um,这两个截距是两个特殊状态下的电流表和电压表的读数,即短路电流Im和断路电压Um,再结合全电路欧姆定律,公式U=E-Ir,可以得出
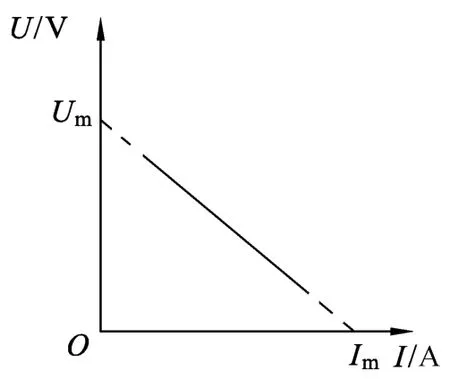
图6
4 自主描绘“物理图像”,发展学生的“视觉-空间”智力
在霍华德·加德纳的《智力的结构》一书中指出,影响个体发展的智力被分为8类,其中的“视觉-空间”智力是一种三维的空间思维能力,如果学生的“视觉-空间”智力强,则他能够准确地感知物理现象的外部和内部特征,并以图形的形式将视觉或空间思维准确地呈现出来.在物理学习过程中,学生画示意图的过程是将一个物理情景或物理问题,与大脑中的记忆表象进行有效链接并将物理情景外显为物理图像的过程.学生画示意图能够实现物理问题“视图化”,学生能够准确画出物理示意图,通常其解译图形信息的能力也较强.
例如,一杂技演员表演走绳索,当其走到绳索中点时,原先水平的绳索现在与水平方向成θ角,求此时绳索上的张力是演员体重的多少倍?
这道题要想正确地解答出来,需要学生从大脑中提取生活现象,将走钢丝的物理情景抽象为简单的物理模型,并用示意图的方式呈现出来,如图7所示.实现了物理问题的“视图化”,该问题也就迎刃而解.
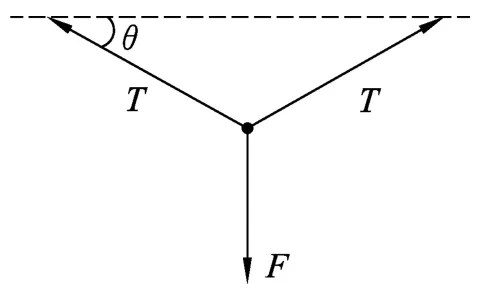
图7
“绘画是一种描述”,不同的学生由于“视觉-空间”智力水平的差异,会导致示意图表现意象的清晰度、完整性有差异.但是教师在平时的物理教学过程中,只要坚持针对性培养学生画示意图的意识,通过有序的训练,学生“看、想、画”的能力必然会稳步提升,对物理意象的理解会更整体化、准确化、多维化.
运用代数的方法解决物理问题,运算往往较为复杂.运用画函数图像的方法,可以定性或定量地得到答案,实现物理过程及结果的“视图化”.
例如,一个物体做匀变速直线运动,已知时间t内通过的路程为s,试比较该物体在中间位置的速度v1和中间时刻的速度v2的大小关系.
处理这个问题时,假如根据公式,需同时考虑加速和减速两种情况,即分为a>0和a<0两种情形讨论,通过解方程组比较v1和v2的大小关系,对于高一的学生而言计算要求过高,往往耗时而不得其解.
如果能引导学生分别画出物体做匀加速和匀减速两种情形的v-t图像,分别如图8(a)、(b)所示.两种情形中,中间时刻的速度可以直接通过坐标找出,中间位置的速度可以根据将图形划分成的梯形面积相等找到.通过两幅图形的对比,可以清晰地看出无论是匀加速运动还是匀减速运动,都有v1>v2.

图8
物理图像作为图像的一种特殊形式,是学生在高中物理学习这个特殊的时期必不可少的,有其独特的教育价值和功能,在教学中重视物理图像的教学功能,有利于辩证性地发散和集中学生的思维,培养学生创造性思维,提升学生的学习能力.
1 陶洪.物理实验论[M].南宁:广西教育出版社,1999:1-2.
2 吴齐全.浅析用图像法处理实验数据[J].物理实验,2006(3):30-33.

