等角速度旋转容器中液体相对平衡的分析
(上海理工大学能源与动力工程学院,上海 200093)
(上海理工大学能源与动力工程学院,上海 200093)
为了将所学专业知识进行综合运用,采用Fluent软件的层流模型和VOF模型,对离心泵的工作原理——等角速度旋转容器中液体的相对平衡进行数值模拟,得到了流场内速度、压力等分布。结果表明,对等角速度旋转容器中液体的相对平衡问题而言,Fluent软件是一个强有力的研究工具,计算结果与理论分析、相关文献实验结果吻合良好,并且模拟能给出更加丰富的流场信息,研究过程加深了对所学知识的理解。
等角速度旋转;相对平衡;数值模拟;Fluent软件;VOF模型
1 前言
液体的相对平衡是工程实际中常遇到的问题,如在离心式铸造机、离心式水泵中,在等角速度旋转条件下,液体与这些容器处于相对平衡状态[1,2]。以离心泵为例,在泵体内和吸水管内注满水后,利用高速旋转的叶轮带动泵体内的水一起旋转,通过离心力把水甩出叶轮外缘后汇集于逐渐扩大的泵体中。在扩压管中水的动能转化为更高的压力,从而把水压出扩压管。叶轮进口则会形成真空区域,吸水池上的水就会被环境中的大气压压入水管,进入叶轮。叶轮连续旋转,水被不断吸入和排出,如此循环就是离心泵的工作原理[3]。为了对离心泵的工作原理有更直观的理解,并把流体力学、计算流体力学等课程所学知识举一反三地应用,本文采用Fluent软件对等角速度旋转容器中液体的相对平衡问题进行了分析研究。
2 物理模型和网格的生成
本文研究对象为一直径d=9.82cm,高度H=10cm的圆柱容器,注水高度h=5.5cm。使容器绕垂直轴以角速度ω作稳态旋转。如图1所示。
本文考虑二维轴对称情况,使用Fluent软件中的前处理模块Gambit生成计算区域与网格。由于容器的对称性以及Fluent软件的对称轴必须与轴一致,故建模时建立圆柱体的右半区域,待导入Fluent后再镜像与顺时针旋转90°。运用Quad单元与Map方法对计算区域进行面网格划分,其中右侧边和轴线网格为150,节点间距比例为双边0.98;上边和底边的线网格为75,节点间距比例为双边1.02。网格数量最终为11250,如图2所示。

图1 旋转容器中液体相对平衡
3 数学模型
3.1 VOF模型
由于本例含有自由液面流动,因此计算中采用“流体体积”(Volume of Fluid-VOF)方法求解[4]。

图2 圆柱容器右半侧二维网格图
VOF方法作为一种解决两相流问题的方法,是通过体积函数来追踪相间界面,具有物理概念清晰、容易实现、计算量小以及精度较高等优点。
追踪各相流体的体积分数可以通过连续性方程来求解,例如第 相流体的体积分数可以通过如下的连续性方程求解:
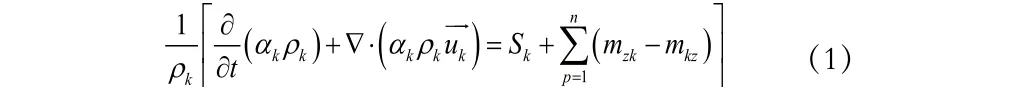
3.2 等角速度旋转容器中液体相对平衡理论分析
根据达朗贝尔原理,作用在液体质点上的质量力包括重力和方向与向心加速度相反的离心惯性力。如图1所示,作用在单位质量液体质点上的质量力的分量为:

根据流体的平衡微分方程式得:

把(2)、(3)、(4)式代入(5)式可得:

将上式积分可得旋转液体中的压强分布规律:

根据边界条件r=0,z=0时, 得到容器中液体的静压强分布公式:

等压面上dp=0,代入式(6),故
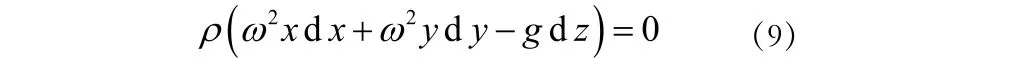
把上式积分并代入自由表面处r=0,z=0得到自由表面方程为

其中,

在r=R处,有

其中,r为液体质点所在的半径,hmax、hmin分别为旋转液面最高处和最低处到容器底部的距离。从(8)式可以看出,在做等角速度旋转容器中处于相对平衡的液体,其等压面为旋转抛物面。
3.3 计算参数和边界条件
3.3.1 计算参数
为与文献[5]中实验结果进行比较,旋转角速度分别设为11.519rad/s、12.043rad/s、12.566rad/s、13.090rad/s、13.614rad/s、14.137rad/s这六种情况进行模拟,重力加速度g=9.793m·s-2。
3.3.2 边界条件
自由液面为压力入口,其值为大气压;右侧边和底边设为旋转壁面,满足无滑移条件;轴线处取为轴对称边界条件。
4 模拟结果分析
4.1 速度矢量图
因为在六种角速度下的模拟结果基本类似,故取角速度为11.519rad/s时的结果进行讨论。
图3为流场速度矢量图分布,其中图(a)为整体速度分布。为了便于观察分析,在流场中选取了四个区域,对其进行局部放大,其速度矢量分布如(b)、(c)、(d)、(e)所示。
由图3(b)可看出,液体的速度方向垂直于截面指向外,说明液体与壁面无相对运动,成为一个整体随容器一起做旋转运动,而且在离心惯性力的作用下稍向壁面甩。液体距中心越远处,外甩现象越明显。由图3(c)所示,由于部分液体外甩,造成容器中部压强下降。空气在大气压的作用下下沉,同时随容器做旋转运动。再由图3(d)和图3(e)可得到,空气下沉碰到液面后改变方向,并在靠近容器出口处有微量回流。
试想,若把容器液面的上方换成一个与大气接触的充满水的吸入室,而容器与水接触的壁面换成逐渐扩大的泵体,则容器内的水不会再沿壁面上升,而是往泵体出口甩,借助动能转变而来的高压甩出泵体。此时,容器中心形成真空,在与大气压的压差作用下,把吸入室内的水压入补充。由于容器的连续旋转,水不断被排出和补充,正好符合水泵的工作现象。
同时,图3(d)和图3(e)中的空气涡流也反映出离心泵中所存在的导致效率降低的问题:在离心泵的吸入室管路中可以找到明显的涡流,这不仅影响叶轮的进口形状,同时还影响着泵的流量与扬程[6,7]。
4.2 压力随液体淹没深度的变化
图4为ω=11.519rad/s时模拟所得相对压力云图。由可看出,在离心惯性力和重力作用下,随液体淹没深度的增加,压力逐渐增大,容器底部靠壁面处压力最大。且等压面为一曲面,为证实其为理论公式预测的抛物线,在流场中建立直角坐标系,取液面最低处为坐标原点,如图1所示,根据液体的静压强分布公式(9)画出一系列抛物线,与截面、等压面的交线进行比较。

图3 速度矢量图

图4 模拟所得压力云图
由图5可得到,在z=-0.0068m、-0.0268m、-0.0468m处,模拟和理论预测的液体压力分布吻合良好。
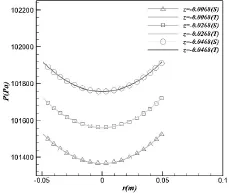
图5 水平面压力随半径分布图(T代表理论值,S代表模拟值)
4.3 利用旋转液面最高与最低处的高度差测重力加速度
由公式(12)可得,已知自由液面最低点和最高点的高度差、旋转速度和容器半径即可求得重力加速度。结合以上分析,由于液体和容器相对平衡时液面呈旋转抛物面(如图6所示),则液体的最低点、最高点分别在容器的对称轴、侧边与液面的交界处,为寻找气液两相间的分界点,从而求得两者高度差Δh=hmax-hmin,最低点hmin取体积分数在区间(0.5,0.7)内的点,最高点hmax由于考虑到液体随转速增大有可能溢出容器边缘的问题,而取体积分数(0,0.2)的点,结果见表1和表2。
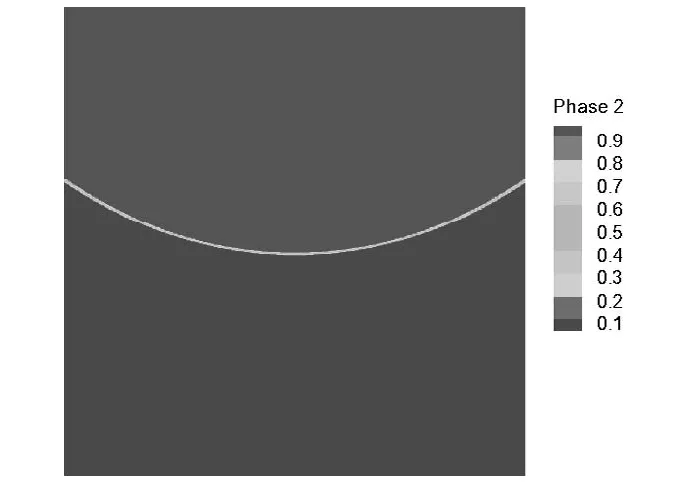
图6 气相云图

表1 不同转速下最低点和最高点值表
由表1可得到,随着旋转角速度的增大,液面靠壁面处上升高度越大,轴线处下降深度也越大。

表2 重力加速度值表
实验中,由于测量精度不高造成液面的最高处和最低处间Δh存在误差,使实验数据与公认值不一致。而数值模拟中存在:①建模过程中的误差;②离散误差;③舍入误差。因此无法完全准确读出水体积分数完全相同的一系列点,致使模拟所得到的Δh值与实际存在误差。在一定程度下,网格越细,模拟得到的Δh越精确,结果越接近公认值。但网格并非越细越好,过分细密的网格会大大增加计算机的运算次数,导致舍入误差增大[8]。
5 结论
(1)理论流体力学是把真实物理现象抽象为数学模型,通过计算、推导获得解析表达式,用以描述生活中的现象,其结果相对精确;而计算流体力学则通过云图和速度矢量图等计算结果直接观察到容器旋转时,液面随之变化的状态和速度分布,但在计算过程中存在一些误差。若把两者结合使用,既可验证理论分析的正确性,又有利于加深理解离心泵工作时的内部流体运动情况,把抽象的公式转换为更形象的生活现象。
(2)在重力和离心惯性力作用下,等角速度旋转容器内的液体,在相对平衡时自由表面和等压面均会形成绕z轴的旋转抛物面。采用层流模型和VOF模型对等角速度旋转容器中液体的相对平衡具有较好的模拟,计算结果与理论分析、实验结果吻合良好。
(3)模拟也很好地证实了利用旋转液面最高和最低处的液位差测重力加速度的方法确切可行。
[1]归柯庭,汪军,王秋颖.工程流体力学[M].北京:科学出版社,2003.
[2]杜广生.工程流体力学[M].北京:中国电力出版社,2007 .
[3]周砚梅.谈离心泵的工作原理与检修[J].黑龙江科技信息,2012(30):84.
[4]朱红钧,林元华,谢龙汉.FLUENT流体分析及仿真实用教程[M] .北京:人民邮电出版社,2010.
[5]陈红雨.旋转液体综合实验设计[J].大学物理,2007,26 (01):29-33.
[6]Congxin Yang,Yuntong Ma.Investigation on the Internal Flow in a Boiler-Feeding-Water Pump Powered By A Gas-Turbine[C]//International Conference on Materials for Renewable Energy and Environment (ICMREE),2013,3:759-762.
[7]韩永阳,王巧莲,徐斌.离心泵入口侧涡流对管路影响试验研究[J].山西水利,2013,29(12):23.
[8]陶文铨.数值传热学(第2版)[M].陕西:西安交通大学出版社,2001.
等角速度旋转容器中液体相对平衡的分析
方海林,杨 帆
方海林(1993—),女,广东茂名人,本科,主要从事:cfd数值模拟研究。

