月地返回轨道误差分析和第一次中途修正时机

郑爱武，周建平，胡松杰

（1.航天飞行动力学技术重点实验室，北京100094；2.北京航天飞行控制中心，北京100094；3.中国载人航天工程办公室，北京100720）

·工程技术·

月地返回轨道误差分析和第一次中途修正时机

郑爱武1，2，周建平3，胡松杰1，2

（1.航天飞行动力学技术重点实验室，北京100094；2.北京航天飞行控制中心，北京100094；3.中国载人航天工程办公室，北京100720）

分析了月地返回飞行过程中的误差因素和量级采用蒙特卡洛法和统计理论，定量分析了月地返回轨道入轨时刻误差、入轨状态误差、入轨控制误差、转移段定轨误差、中途修正控制误差等各种误差对轨道终端参数的影响。给出了月地返回轨道中途修正的计算步骤，然后以预期再入时刻和目标再入点为修正目标，采用微分改正法计算中途修正所需的速度增量。结合误差分析结果和测控条件，给出第一次中途修正时机的建议和一个具体算例，计算结果表明所提中途修正方法和策略可以修正入轨误差、定轨误差和控制误差的影响，使月地返回轨道可以按预期的再入时刻返回预定再入点。

月地返回轨道；误差分析；蒙特卡洛法；中途修正

1 引言

在飞行任务中，存在很多不可避免的误差，比如入轨误差、定轨误差、轨道控制误差以及轨道预报误差。目前对地月转移轨道的中途修正问题进行分析的论文较多［1-3］，而对月地返回轨道及其中途修正进行研究的论文很少。作者曾采用协方差法，建立轨道误差传播方程，对月地返回轨道的最后一次中途修正的时机和分离高度选择进行了专门的研究［4］，但没有涉及其他中途修正。事实上，整个月地转移过程中实施概率最大的应该是第一次中途修正。以Apollo11为例，任务前计划了3次中途修正，分别为月地返回轨道入轨后15小时，再入前22小时和再入前3小时。在实际飞行任务中，仅实施了第一次中途修正［5］。因此，作为对协方差法的补充，本文重点对第一次中途修正进行研究。由于在月球影响球附近时摄动力有大的变化，不容易给出解析解，因此本主要采用蒙特卡洛法和统计理论考察各种误差对轨道的影响及其大小。然后以预期再入时刻、目标再入点和再入角为修正目标，采用微分改正法计算中途修正所需的速度增量。结合误差分析结果和测控条件，给出第一次中途修正时机的建议和一个具体算例，以验证本文提出的中途修正方法和第一次中途修正策略的正确性和可行性。

2 月地返回误差分析

2.1 月地返回轨道的误差因素及量级

月地返回轨道中途修正是为了消除月球探测器在月地转移飞行过程中产生的相对标称轨道的偏差，使探测器能够沿设计的转移轨道到达预定再入点，并使再入角限定在再入走廊内。因此，首先需要分析返回过程中的误差因素、误差量级及其对轨道和终端状态的影响。影响月地返回轨道精度的误差主要有入轨时刻误差、入轨状态误差、入轨控制误差、转移段定轨误差、中途修正控制误差等。根据嫦娥一号和二号任务的经验，误差的量级近似如表1所示。本文所用到的坐标系见参考文献［6］。

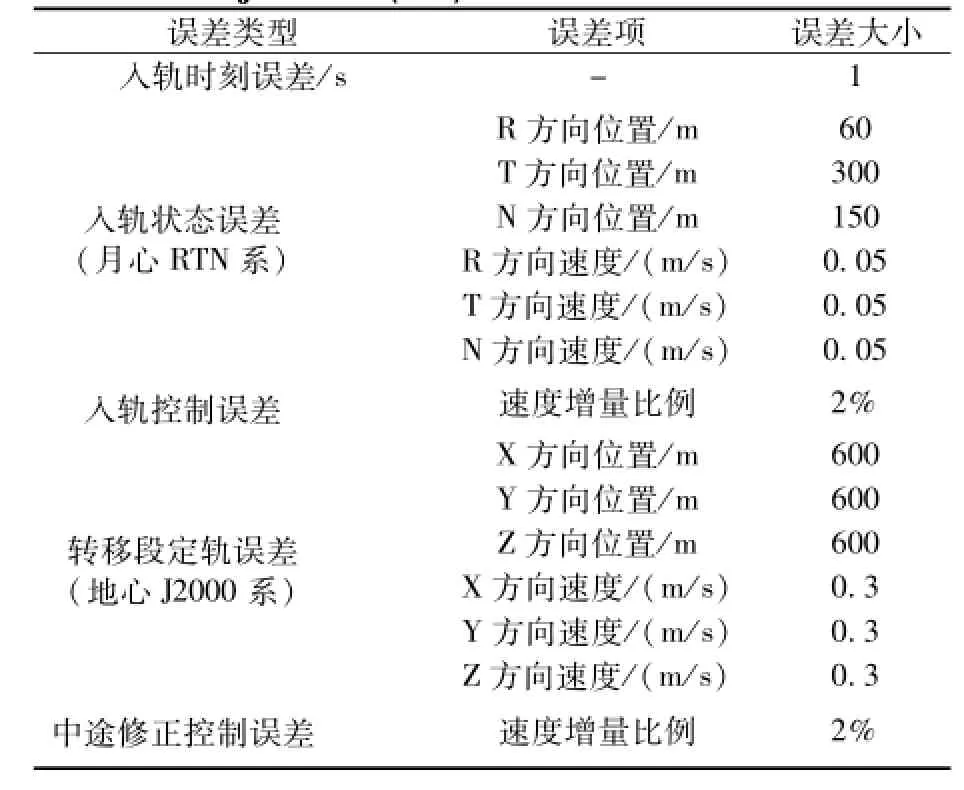
表1 月地返回轨道的误差因素及其量级（3σ）Table 1 Errors and their magnitudes of M oon-to-Earth trajectories（3σ）

下面选取一条月地返回轨道作为标称轨道［7，8］，轨道参数见表2，具体分析各类误差对该轨道终端参数的影响。轨道终端参数主要指飞行时间或再入时刻、再入点位置和再入角大小。

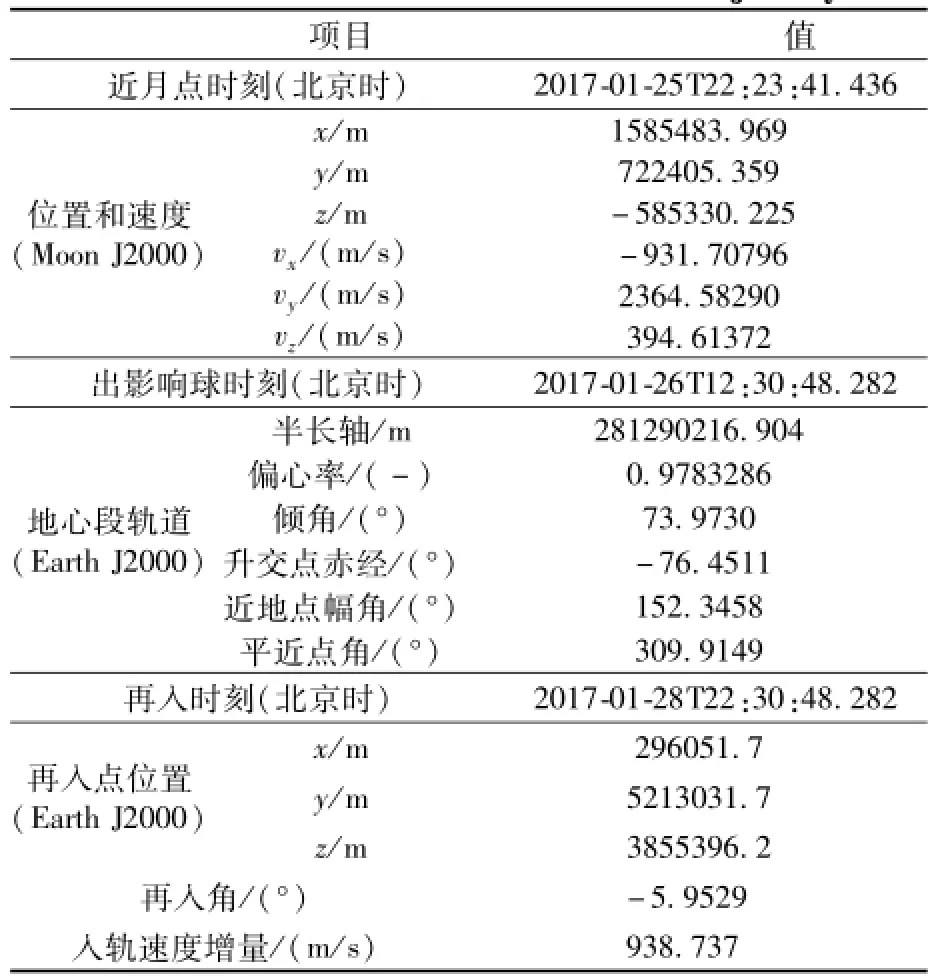
表2 标称月地返回轨道Table 2 A nom inal M oon-to-Earth trajectory

2.2 误差对终端约束条件的影响

2.2.1 入轨时刻误差对终端参数的影响

根据工程经验，由于环月段的定轨精度和轨道预报精度较高，入轨时刻和入轨点位置和速度的预报精度较高。入轨时刻误差主要有两种情况，一种是由跳秒引起的时刻上的偏差，而入轨状态即位置和速度不变。另一种是由于星地时差引起的入轨时刻和入轨状态的偏差。下面分别对这两种情况进行分析。

第一种情况，仅考虑入轨时刻误差。这里入轨时刻误差取±1 s的情况，然后将探测器位置和速度由入轨点外推至再入面（距地面120 km高的球面），计算终端参数，结果见表3。可以看出，1 s左右的入轨时刻误差对终端参数的影响很小，再入点位置误差不到0.5 km，可以忽略。

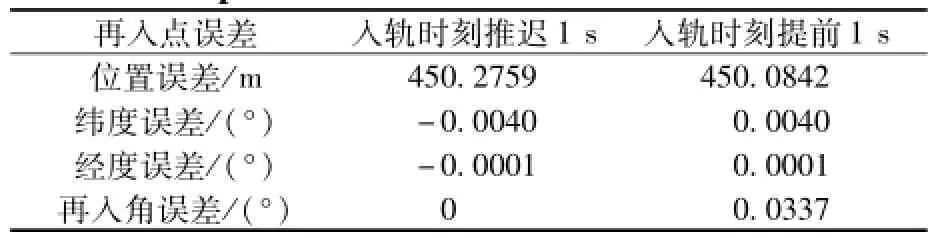
表3 入轨时刻误差对终端参数的影响Table 3 Impacts of TEI time bias on the orbit term inals

第二种情况，入轨时刻误差也带来了入轨状态的变化，比如提前或推迟实施月地返回轨道入轨机动。这种情况主要是由星地时差引起的。根据嫦娥卫星任务的实际飞行经验，星地时差不会超过5 ms，否则就要安排校时。这里不妨取10 ms进行分析。假设由于星地时差，卫星实际上提前10 ms或推迟10 ms实施入轨机动，入轨的速度增量不变，则可以计算出在预定的入轨时刻，实际位置和速度与预定的入轨位置和速度之间的偏差，计算终端参数，结果见表4。可以看出，10 ms星地时差导致的入轨时刻和状态误差对终端参数的影响也很小，仅导致再入点约14 km的位置偏差。

表4 入轨时刻和状态误差对终端参数的影响Table 4 Im pacts of TEI time bias and status errors on the orbit term inals

以上两种情况都说明，入轨时刻误差对终端参数的影响较小。由于第一种情况影响更小，可以忽略，因此下面的误差叠加中主要考虑叠加第二种情况的入轨时刻误差。

2.2.2 入轨状态误差对终端参数的影响

入轨状态误差是在月心RTN坐标系下给出的，其在沿迹方向即T方向误差最大。单独将入轨状态误差按高斯分布生成500组偏差，通过坐标转换为月心J2000坐标系下的位置和速度偏差，然后分别叠加到近月点上，外推至再入时刻，计算终端参数，并统计误差结果，见图1和图2。从结果可以看出，入轨的状态偏差对轨道的影响非常大，再入点偏差约601 km，实际再入角也可能超出再入走廊的范围。

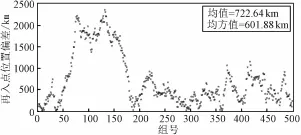
图1 入轨状态误差引起的再入点位置偏差Fig.1 Reentry position deviation caused by status errors of TEI

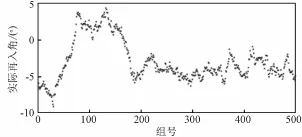
图2 入轨状态误差引起的再入角Fig.2 Reentry angle caused by status errors of TEI

2.2.3 入轨状态误差和时刻误差对终端参数的影响

假设由于星地时差，卫星实际上提前10 ms或推迟10 ms实施月地返回轨道的入轨机动，入轨的速度增量不变，将卫星星历积分（或反向积分）至近月点，然后叠加上入轨状态误差，外推至预定再入时刻，计算终端参数，结果见图3～图6。

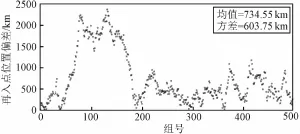
图3 入轨状态误差+提前10 m s入轨的再入点位置偏差Fig.3 Reentry position deviation caused by status errors and 10ms earlier of TEI

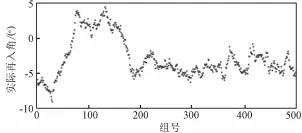
图4 入轨状态误差+提前10ms入轨的再入角Fig.4 Reentry angle caused by status errors and 10 m s earlier of TEI

可以看出，误差叠加后对终端参数的影响并不是简单的放大，对位置偏差的影响比较明显，对实际再入角的影响不明显，由于入轨状态误差影响较大，故误差叠加后的终端参数曲线的形状与图1和图2相似，数值上有平移。

2.2.4 入轨控制误差对终端约束条件的影响

假设入轨速度增量为900 m/s，按2%的比例误差计算即为18 m/s（速度方向），单独将入轨控制误差按高斯分布生成500组偏差数据，坐标转换后叠加到近月点速度上，计算终端参数，并统计误差结果，见图7和图8。可以看出，入轨控制误差对轨道的影响非常大，如果不及时加以修正，将导致约38762 km的再入点偏差，实际再入角远远超出再入走廊的范围。

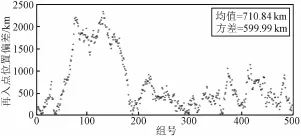
图5 入轨状态误差+推迟10 m s入轨的再入点位置偏差Fig.5 Reentry position deviation caused by status errors and 10ms later of TEI

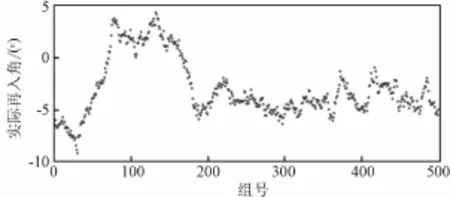
图6 入轨状态误差+推迟10ms入轨的再入角Fig.6 Reentry angle caused by status errors and 10ms later of TEI

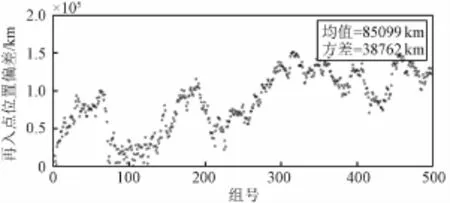
图7 入轨控制误差引起的再入点位置偏差Fig.7 Reen try position deviation caused by TEI control errors

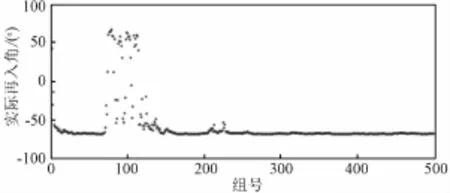
图8 入轨控制误差引起的实际再入角Fig.8 Reentry angle caused by TEI control errors

2.2.5 入轨控制误差叠加入轨误差后对终端参数的影响

在入轨控制误差上同时叠加入轨时刻误差和入轨状态误差，分析这3种误差都存在时对终端参数的影响。计算结果见图9～12。可以看出，误差叠加后的终端关系曲线与图7和图8相似，在数值上有小的变化。

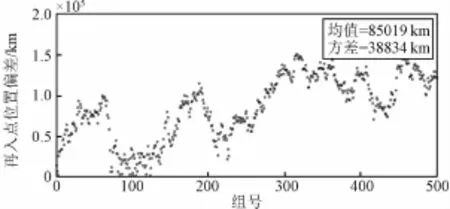
图9 入轨状态误差+提前10 m s入轨+入轨控制误差引起的再入点位置偏差Fig.9 Reentry position deviation caused by status errors，10m s earlier and control errors of TEI

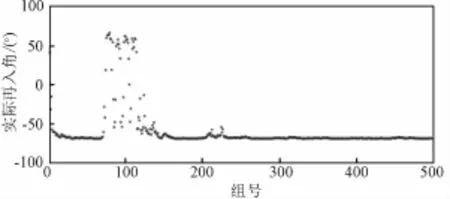
图10 入轨状态误差+提前10 m s入轨+入轨控制误差引起的实际再入角Fig.10 Reentry angle caused by status errors，10m s earlier and control errors of TEI

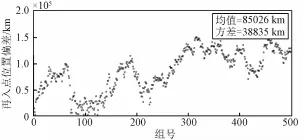
图11 入轨状态误差+推迟10 m s入轨+入轨控制误差引起的再入点位置偏差Fig.11 Reen try position deviation caused by status errors，10 ms later and control errors of TEI

2.2.6 转移段定轨误差对终端参数的影响

假设入轨后15小时进行第一次中途修正，单独将该误差按高斯分布生成500组偏差，叠加到中途修正点的位置速度上，计算终端参数，误差统计结果见图13和图14。

从结果可以看出，转移段的定轨偏差对轨道的影响比入轨状态误差对轨道的影响小，可以导致约74 km的再入点偏差，但实际再入角可能超出再入走廊的范围。

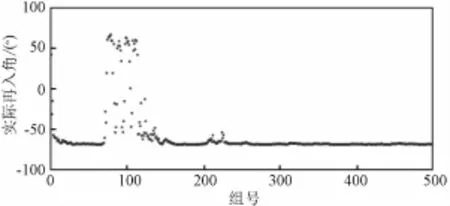
图12 入轨状态误差+推迟10 m s入轨+入轨控制误差引起的实际再入角Fig.12 Reentry angle caused by status errors，10 m s later and control errors of TEI

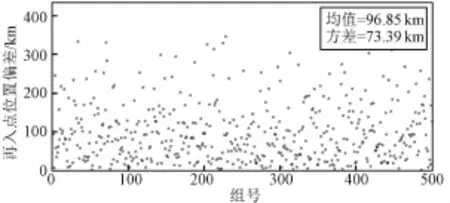
图13 转移段定轨误差引起的再入点位置偏差Fig.13 Reentry position deviation caused by orbit determ ination

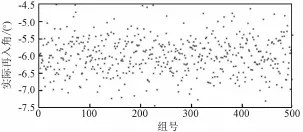
图14 转移段定轨误差引起的再入角Fig.14 Reen try angle caused by orbit determ ination

2.2.7 中途修正控制误差对终端参数的影响

假设入轨后15小时进行第一次中途修正，修正量为5 m/s，按2%的速度大小比例误差计算即为0.1 m/s，单独将该误差按高斯分布生成500组偏差，分别叠加到中途修正点的位置速度上，计算终端参数，并统计误差结果，见图15和图16。从结果可以看出，中途修正的控制偏差对轨道的影响较小，不修正的情况下将导致约25 km的再入点偏差，对再入角影响不大。

2.2.8 中途修正控制误差和转移段定轨误差对终端参数的影响

同时考虑上述中途修正控制误差和定轨误差，计算终端参数，误差统计结果见图17和图18。可以看出，误差叠加后对终端参数的影响加剧。

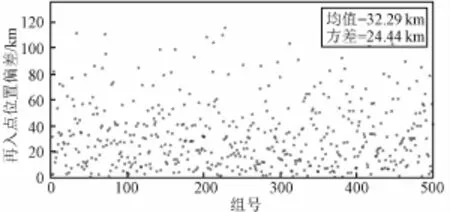
图15 中途修正控制误差引起的位置偏差Fig.15 Reen try position deviation caused by control errors ofm idcourse correction

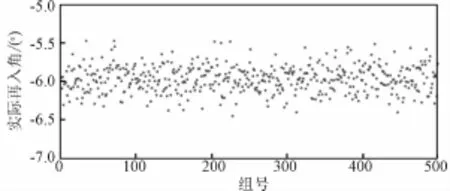
图16 中途修正控制误差引起的实际再入角Fig.16 Reentry angle caused by control errors ofm idcourse correction

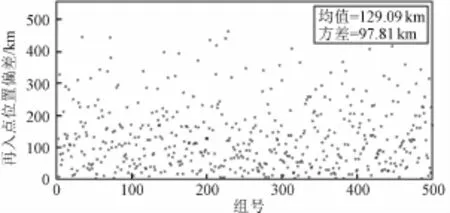
图17 中途修正控制误差+定轨误差引起的偏差Fig.17 Reentry position deviation caused by control errors of m idcourse correction and orbit determ ination

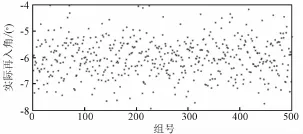
图18 中途修正控制误差+定轨误差的再入角Fig.18 Reentry angle caused by control errors ofm idcourse correction and orbit determ ination

综上所述，通过分别考察入轨时刻误差、入轨状态误差、入轨控制误差、转移段定轨误差、中途修正控制误差等5类误差以及多种误差叠加后对终端参数的影响可以发现，在这5类误差中，入轨控制误差对轨道的影响最大，其次是入轨的状态偏差，转移段的定轨偏差对轨道的影响也较大，而中途修正的控制偏差（按5 m/s考虑）对轨道的影响比较小。另外，入轨时刻误差对终端参数的影响最小，导致的再入点偏差不到15 km。误差叠加后，对终端参数的影响也增加。其中，主要的误差因素决定了终端参数曲线的形状。各类误差导致的再入点位置偏差的统计结果见表5。

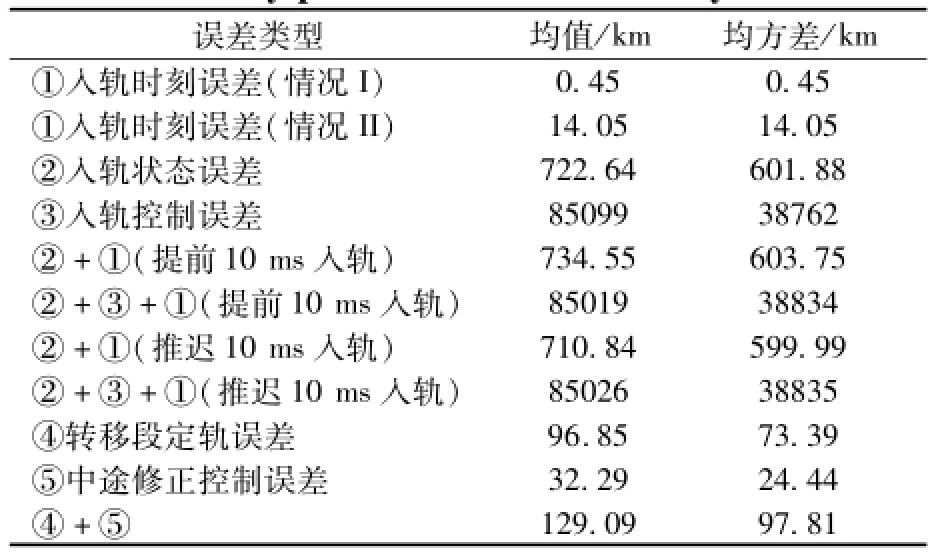
表5 由各种误差引起的再入点位置偏差Table 5 Reentry position deviation caused by main errors

由于这些误差的存在和传播，如果不进行中途修正，可能导致探测器无法正常返回，因此必须实施至少一到两次中途修正。

3 月地返回轨道中途修正策略

3.1 中途修正的计算步骤

月地返回轨道的中途修正采用基于线性摄动的微分改正法［8］进行计算，计算步骤如下：

步骤1：由当前时刻t（即中途修正时刻）和理论再入时刻Tentry计算剩余飞行时间；

步骤2：采用摄动模型用数值法从当前点积分Δt时间后得到再入时刻的位置，计算该位置与理论再入点的位置偏差，用微分改正法修正中途修正点的速度矢量，直到再入点位置误差满足容差；

步骤3：计算中途修正速度增量Δv=vnewv0，vnew为最后得到的中途修正点速度，v0为原来的速度矢量；

步骤4：计算修正后的再入角，判断是否满足再入走廊要求；如果不满足要求，则转入应急轨道设计。

3.2 月地返回轨道测控条件分析

中途修正策略的制定除了考虑误差分析的结果外，载人的情况下还要考虑航天员的工作-休息时间，另外还必须考虑测控条件。为了防止轨控过程发生意外，一般要求变轨过程处于测控站的跟踪范围内，并且要求双站共视。根据国内的测控资源，考虑喀什站、青岛站和佳木斯站对月球探测器进行测控。在实际工程中，如果需要用VLBI（Very Long Baseline Interferometer）测量系统得到的角度数据联合定轨，还需要考虑VLBI测量站的跟踪情况，比如变轨后有足够的时间保证三个VLBI站共视。在嫦娥一号和嫦娥二号任务中，通过将测站数据和VLBI数据联合定轨，大大提高了定轨精度，特别是在距离比较远的情况下［9］。国内4个VLBI站分别为北京站、昆明站、上海站和乌鲁木齐站。将表1的轨道作为标称轨道，计算3个测控站和4个VLBI站的跟踪情况，跟踪预报图见图19。由测控条件可以看出，月地返回轨道入轨后10～15小时约有5小时的连续测控弧段，可以作为实施第一次中途修正的可选择时段。

图19 测站跟踪预报图（UTC）时间Fig.19 Station tracking forecast

4 第一次中途修正设计算例

影响第一次中途修正修正量的误差主要有两类：入轨控制误差和入轨状态误差。入轨时刻误差影响很小，这里不考虑。由表1可知入轨所需速度增量为938.737 m/s，乘以2%比例误差后为18.8 m/s，加上入轨状态误差后按高斯分布生成的一组误差量，转换为月心J2000坐标系下的分量后叠加至入轨初始状态上，分别在传播了1～72小时后实施中途修正，计算所需的中途修正量及实际再入角，计算结果见图20和图21。

由图20可以看出，当第一次中途修正时刻推迟至50小时后，所需的速度增量急剧增加。这主要是误差随着轨道的传播被逐渐放大的缘故。如果要保证第一次中途修正所需的速度增量不超过15 m/s，则第一次中途修正时刻不能超过19小时。图21为修正后轨道的再入角，可以看出，第一次中途修正时刻越迟，则实际的再入角越大，至60小时后，再入角急剧增大。如果要保证实际再入角不超出再入走廊的上限即-6.2°，则第一次中途修正时刻不能超过55小时。综上所述，第一次中途修正的时机不能太晚，否则将导致中途修正所需的速度增量过大。

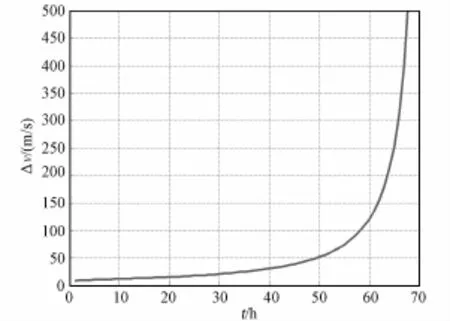
图20 中途修正速度增量Fig.20 Velocity increm ent ofm idcourse correction

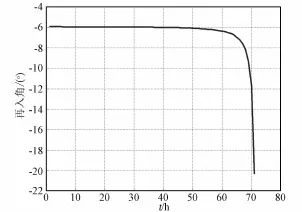
图21 中途修正后实际再入角Fig.21 Reentry angle after m idcourse correction

综合误差分析结果和测控条件分析，可以取第一次中途修正的时刻点为入轨后14小时或15小时，变轨满足双站共视条件，变轨后仍然有3～4小时的测控跟踪和2～3小时的VLBI站测量，满足定轨条件。分别在入轨后14小时和15小时实施第一次中途修正，则修正量的计算结果见表6和表7。

表6 第一次中途修正速度增量（14小时）Table6 Velocity increment of the firstm idcourse correction in 14 hours later than TEI

表7 第一次中途修正速度增量（15小时）Table7 Velocity increment of the first m idcourse correction in 15 hou rs later than TEI

5 结论

本文分析了影响月地返回轨道精度的误差因素，针对一条标称轨道，采用蒙特卡洛法，分别考察了入轨时刻误差、入轨状态误差、入轨控制误差、转移段定轨误差、中途修正控制误差等5类误差对终端参数的影响。误差分析结果表明探测器在月地飞行过程中必须实施至少一到两次中途修正。而且第一次中途修正的时机不能太晚，否则误差传播时间增加后将导致修正所需的速度增量也相应增加。然后以理论再入时刻、再入角和再入点位置为修正目标，采用基于线性摄动的微分改正法计算中途修正速度增量，最后综合误差分析结果和国内测控条件，给出了具体的第一次中途修正算例。结果表明本文提出的中途修正方法和策略可以很好地修正入轨误差、定轨误差和控制误差的影响，使月地返回轨道可以按预期的再入时刻返回预定再入点。

［1］ 周文艳，杨维廉.月球探测器转移轨道的中途修正［J］.宇航学报，2004，25（1）：89-92.

［2］ 杨维廉，周文艳.嫦娥一号卫星地月转移轨道中途修正分析［J］.空间控制技术与应用，2008，34（6）：3-7.

［3］ DongHyun Cho，Youngsuk Chung，Hyochoong Bang.Trajectory correction maneuver design using an improved B-plane targetingmethod［J］.Acta Astronautica，2012，72：47-61.

［4］ 郑爱武，周建平，胡松杰.月地返回轨道控制误差传播及分离点位置精度分析［J］.系统工程与电子技术.2012，34（12）：2529-2534.

［5］ Ronald L.Berry.Launch Window And Translunar，Lunar Orbit，and Transearth Trajectory Planning and Control for the A-pollo 11 Lunar Landing Mission［C］//AIAA 8th Aerospace Science Meeting，New York，January 19-21，1970.

［6］ 刘林，侯锡云.深空探测器轨道力学［M］.北京：电子工业出版社，2012：348-368.

［7］ 郑爱武，周建平，刘勇.月地转移轨道快速设计方法研究［J］.北京航空航天大学学报，2014，40（3）：344-349.

［8］ 郑爱武，周建平.月地转移轨道精确轨道设计［J］.飞行器测控学报，2014，33（1）：52-58.

［9］ 黄勇.“嫦娥一号”探月飞行器的轨道计算研究［D］.上海：中国科学院上海天文台，2006.

Error Analysis of M oon-to-Earth Trajectory and Choice of the First M idcourse Correction

ZHEGN Aiwu，ZHOU Jianping，HU Songjie
（1.Key Lab of Spaceflight Dynam ic Tehnology，Beijing 100094，China；2.Beijing Aerospace Control Center，Beijing100094，China；3.China Manned Space Agency，Beijing 100720，China）

The error factors and their level in the flight of Moon-to-Earth trajectory were analyzed. Based on a specified Moon-to-Earth return trajectory，Monte Carlo method and statistical theory were used to quantitatively analyze the impactof themain errors on the terminals of the orbit including time bias and position error of transearth insertion（TEI），orbit control error，orbit determination error and midcourse correction error，and etc.The calculation steps ofmidcourse correction of Moon-to-Earth trajectories were given.Then using the specified reentry time and the reentry point as the correction targets，differential correctionmethod based on linear perturbation wasadopted to calculate the velocity increment of the midcourse correction.Then combined with measurement and control conditions，the firstmaneuver opportunity ofmidcourse correction was determined and a specific sample was given.The results show that themidcourse correction method and strategy suggested in this paper can well amend the influence of the TEIerror，orbitdetermination error and orbit controlerror.The Moonto-Earth trajectory can return to the specified reentry point at the expected reentry moment.

Moon-to-Earth trajectory；error analysis；Monte Carlomethod；midcourse correction

V412.4

A

1674-5825（2014）04-0283-07

2013-12-03；

2014-06-25

国家自然科学基金（11173005）；国家自然科学基金（11203003）

郑爱武（1974-），女，博士，高级工程师，研究方向为航天测控任务总体、轨道设计、轨道确定。E-mail：awzheng@163.com