考虑地球自转的探月返回反馈线性化跟踪制导律设计*
王泽国,孟 斌
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
0 引言
近些年,多国对探月任务表现出极大兴趣,其中探月返回再入制导是探月任务中需要解决的关键技术.再入制导方法中一种常用的方法是标准轨道法,分为轨迹规划和轨迹跟踪两部分内容,分别是设计离线参考轨迹以及设计在线轨迹跟踪制导律[1].
对于轨迹跟踪问题,一般采用反馈线性化方法.航天飞机的轨迹跟踪制导律即采用了一种类似的反馈线性化方法[2-3].Roenneke 等[4]针对一种小升阻比飞行器设计了反馈线性化方法跟踪制导律.Garcia-Llama[5]针对跳跃式再入轨迹中的初次进入段设计参考轨迹及反馈线性化跟踪制导律.上述文献均未考虑地球自转的影响.探月返回一般采用的是跳跃式再入轨迹.跳跃式轨迹所需飞行时间较长,并且探月返回飞行器升阻比较低,地球自转对于制导精度具有更大影响.当考虑地球自转时,再入动力学更加复杂,给制导律的设计带来一定困难.因此,研究考虑地球自转的制导律设计问题具有重要意义.
本文研究考虑地球自转的探月返回跳跃式再入的纵向平面轨迹跟踪问题.首先介绍了航天飞机反馈线性化跟踪制导律,分析了地球自转对于航天飞机制导精度的影响问题.然后针对考虑地球自转的动力学方程,设计了一种简化的反馈线性化跟踪制导律,并分析了设计机理.最后通过数值仿真验证了制导律的有效性.
1 问题描述和预备知识
考虑纵向平面动力学方程[6]
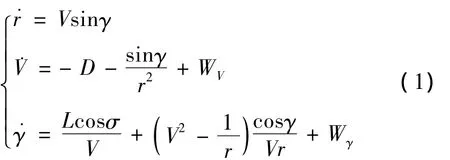
其中,
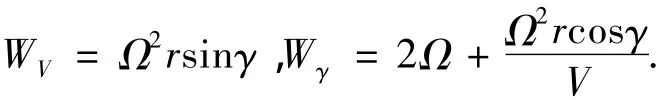

本文考虑探月返回跳跃式再入的纵向平面轨迹跟踪问题.由于D容易测量、易于航程计算以及满足轨迹过载约束,一般选取D作为跟踪变量[7].本文针对式(1)设计σ,使得D跟踪参考阻力.
本文设计了一种简化的反馈线性化跟踪制导律.针对反馈线性化方法的设计要求,在文献[7]中,研究了纵向动力学(1)的性质,为制导律的设计提供了基础.下面给出相关假设和引理.
假设1.在跳跃式轨迹中,记飞行器跃出大气层时的状态为(rt,Vt,γt).跃出后远地点地心距rA可以表示为
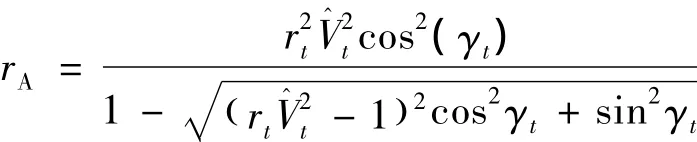
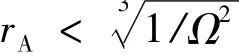
注1.一般来说,假设1在实际中是满足的.当rA较大时,大气层外飞行时间较长,容易导致二次再入误差较大.因此一般情况下假设2.将阻力按照的符号进行分段.对于D·≥0(不包括仅=0的单点情形)和<0段,记各段的时间长度为Ti,i=1,2,… .假设
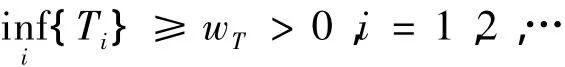
这里wT为常数.
引理1.针对式(1),当cosγ≠0时,如果选择D作为输出,那么式(1)的相对阶为2;并且由状态(r,V,γ)到状态(D,D·,V)的坐标变换为微分同胚变换.
引理2.针对式(1),如果假设1和2成立,则速度内动态是有界输入有界状态的.
一般来说,假设2是满足的,结合注1可知,引理1和2成立.在此基础上,可以针对(D,D·)的二阶动力学设计反馈线性化跟踪制导律.
2 地球自转对航天飞机反馈线性化跟踪制导律的影响分析
2.1 航天飞机反馈线性化跟踪制导律
航天飞机反馈线性化跟踪制导律是针对不考虑地球自转的动力学方程设计的.当WV=Wγ=0时,将式(1)重写为

在本文中,把相应变量加上划线“-”表示不考虑地球自转时的变量.首先推导阻力微分方程.对


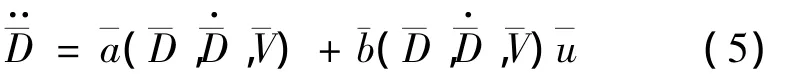
其中,




其中,
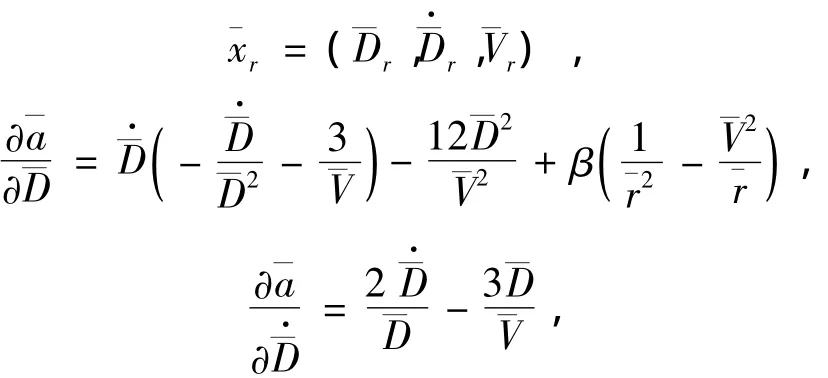
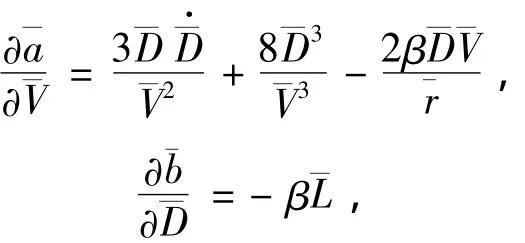
则式(7)转化为

由式(8),可以得到航天飞机反馈线性化跟踪制导律:
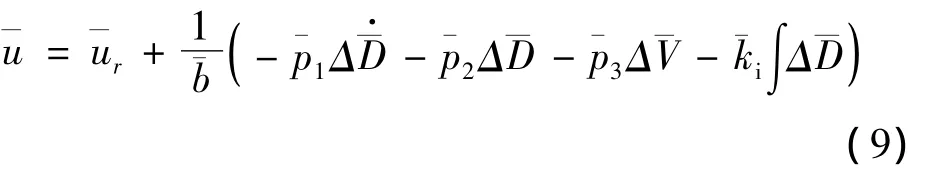
其中,
(3)蓄滞洪区内杆塔采用墩柱式基础,阻水比不足0.001%,壅水高度不足0.0968m,对行洪基本没有影响。31个塔基占用蓄滞洪区容积0.15万m2,不足容积的百万分之八,对蓄滞洪区的运用基本没有影响。

2.2 地球自转影响分析
首先推导考虑地球自转的阻力导数的表达式.由式(2)可得
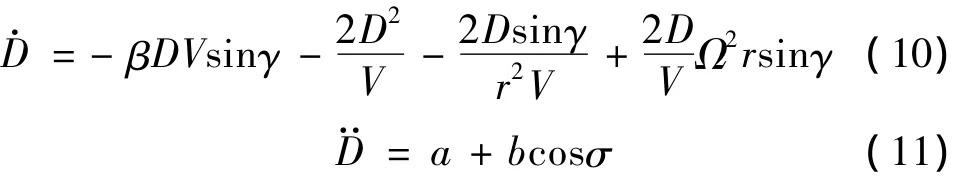
其中

考虑相同状态下地球自转对阻力导数影响,将式(10)和式(4)作差可得
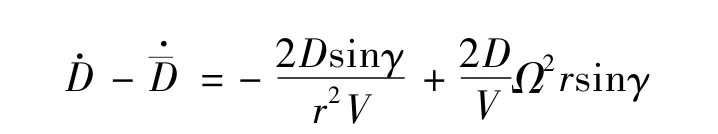
由于γ和Ω较小,并且与它们相乘的量也较小,可见地球自转对于阻力一阶导数的影响很小.因此在下面的推导中假设,进一步由式 (5)和式(11),可以表示为

在式(13)的推导中,由于sinγ和Ω较小,忽略了sinγ与WV,Wγ及自身的乘积,并将sinγ用方程(4)表示[2].比较式(13)与式(5)可知,当考虑地球自转后含有-βDVWγ与 2D2WV/V2两项,其中-βDVWγ影响较大,该项随时间的变化如图1所示,在70 s左右达到了-700左右.从该项的表达式可以看出,阻力对该项有较大影响,所以70 s左右达到最大值.

图1 地球自转对于阻力二阶导数的影响Fig.1 The impact of the Earth rotation on the second derivative of drag
3 考虑地球自转的反馈线性化跟踪制导律设计
首先对式(11)中的a和b进行简化,记为和,即

则式(11)简化为

用Dr表示参考轨迹,则有

其中和是式(14)中和在参考轨迹上的值.由式(15)和式(16)可得
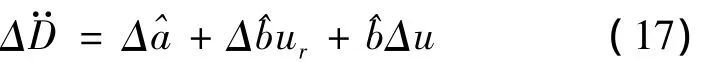
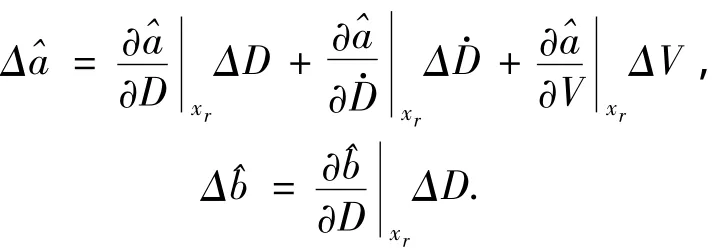
其中,

则式(17)转化为
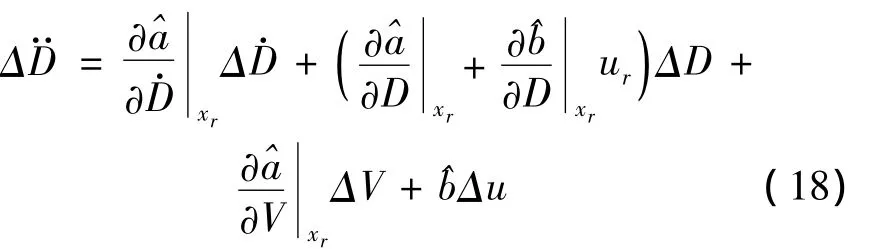
由式(18)设计反馈线性化跟踪制导律

其中,

kd,kp,ki是需要设计的参数.
4 制导律设计机理分析
通过对式(12)中b等号右边的三项进行数值分析可知,其第一项远远大于其他两项,因此,在下面的分析中假设将式(19)代入式(18),并利用式(17),可得
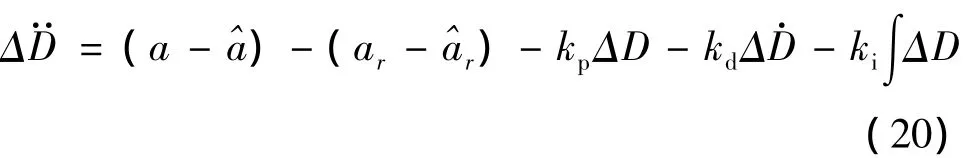
下面从两方面内容分析设计机理.一方面与精确反馈线性化方法比较.如果制导律采用精确反馈线性化方法,那么

与式(20)对比可见上节设计制导律的阻力偏差二阶方程中包含项,所以地球自转对于所设计的制导律仍有影响.
另一方面与航天飞机制导律比较.航天飞机制导律中所跟踪的参考轨迹为,那么

5 数值仿真
本节利用数学仿真研究所设计的跟踪制导律(19)的跟踪效果和鲁棒性,并且与航天飞机跟踪制导律(9)的跟踪效果进行了仿真对比.在数学仿真中,针对考虑地球自转的动力学方程(1),以Apollo作为研究对象,飞行器参数和再入初始状态见文献[9];跟踪曲线Dr通过积分式(1)和式(10)得到,其中输入σ按照文献[9]的方法进行设计;跟踪制导律按照式(19)进行设计,其中参数取kd=450,kp=1 300,ki=500.不确定性考虑初始状态偏差和环境参数偏差,具体取值见表1.在标称情形下阻力跟踪仿真结果和倾侧角曲线如图2~3所示,可见所设计的跟踪制导律可以实现有效跟踪.表2分别给出了本文方法和航天飞机跟踪制导律(9)的仿真结果,其中序号0为标称情形下的仿真结果,序号1~4为不确定情形下的仿真结果,不确定性的具体取值见表1.由表2可知,采用航天飞机制导律时,在情况2下出现较大的阻力跟踪偏差,而采用本文所设计的制导律制导偏差在所考虑情况中均较小,具有更好的跟踪效果.

表1 不同情况下仿真参数说明Tab.1 Simulation parameters in different conditions

表2 不确定性下终点偏差比较Tab.2 Final states deviation comparisons between traditional and proposed methods with uncertainties
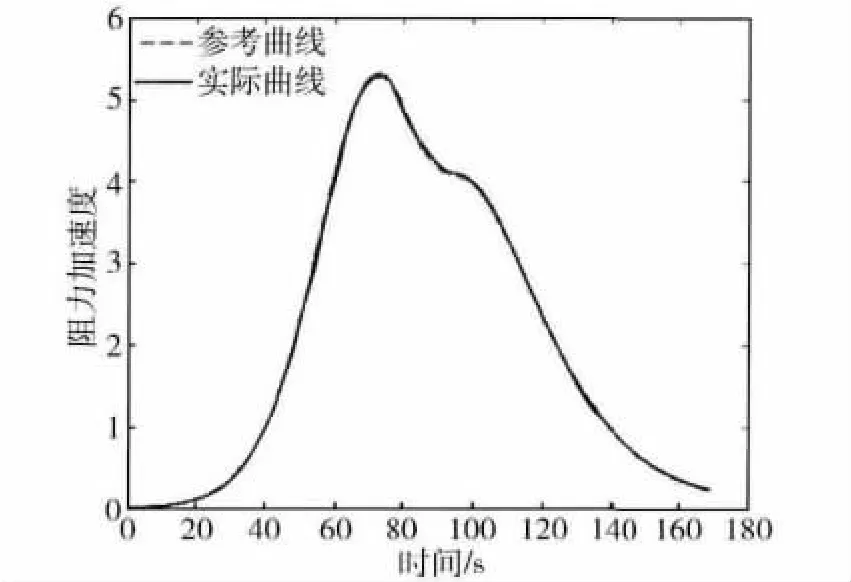
图2 标称状态下阻力跟踪曲线Fig.2 Drag tracking using proposed method with nominal initial states
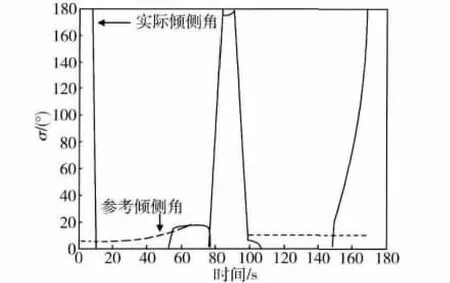
图3 标称状态下倾侧角曲线Fig.3 Bank angle profile using proposed method with nominal initial states
6 结论
本文考虑探月返回飞行器轨迹跟踪问题.通过对航天飞机制导律的介绍,给出地球自转对于阻力跟踪制导律的影响分析.得到地球自转对未引入反馈的航天飞机制导律影响较大以及地球自转影响需要通过反馈设计补偿的结论.最后设计了一种简单的考虑地球自转的反馈线性化跟踪制导律,并分析了设计的机理.在未引入反馈作用时,标称状态下仍具有很好的跟踪效果.而引入反馈作用后,在初始状态偏差和环境不确定性下与航天飞机制导律相比具有更好的跟踪结果,可以有效跟踪阻力参考轨迹.
[1]陈刚,董龙雷,闫桂荣,等.航天器再入制导方法研究现状与发展评述[J].飞行力学,2008,26(1):1-4.CHEN G,DONG L L,YAN G R,et al.Recent status and development review of spacecraft reentry guidance methods[J].Flight Dynamics,2008,26(1):1-4.
[2]MEASE K D,KREMER J P.Shuttle entry guidance revisited using nonlinear geometric methods[J].Journal of Guidance,Control,and Dynamics,1994,17(6):1350-1356.
[3]HARPOLD J C,GRAVES C A.Shuttle entry guidance[J].Journal of Astronautical Sciences,1979,37(3):239-268.
[4]ROENNEKE A J,WELL K H.Nonlinear drag-tracking control applied to optimal low-lift reentry guidance[R].AIAA Paper 96-3698,1996.
[5]GARCIA-LLAMA E.Analytic development of a reference trajectory for skip entry[J].Journal of Guidance,Control,and Dynamics,2011,34(1):311-317.
[6]郭兴玲,张珩.基于分段常滑翔角的长航时纵向远程滑翔飞行方程近似解[J].宇航学报,2005,26(6):712-716.GUO X L,ZHANG H.The approximate solution for long-time and long-range longitudinal gliding flight based on segment constant gliding angle[J].Journal of Astronautics,2005,26(6):712-716.
[7]王泽国.探月返回跳跃式再入制导方法研究[D].北京:中国空间技术研究院,2013.WANG Z G.On the skip entry guidance of lunar return spacecrafts[D].Beijing:China Academy of Space Technology,2013.
[8]MOSELEY P E.The Apollo entry guidance:a review of the mathematical development and its operational characteristics[R].Houston:TRW,1969.
[9]王泽国,孟斌.再入动力学的性质及其在轨迹优化中的应用[J].空间控制技术与应用,2012,38(6):6-12.WANG Z G,MENG B.Properties of reentry dynamics and their application in trajectory optimization[J].Aerospace Control and Application,2012,38(6):6-12.

