基于动量轮的航天器全姿态捕获技术*
王新民,张俊玲,袁 军,柯 旗,宗 红
(北京控制工程研究所,北京100190)
0 引言
航天器往往由于某种原因会出现在轨故障[1],导致姿态丢失,为了恢复卫星姿态,需要充分利用星上条件,采取措施使航天器重建任务姿态.全姿态捕获是指航天器丢失姿态基准而需恢复正常姿态或者定向新姿态时的一种控制过程,一般可以实现3个目的:1)可以使航天器对惯性定向;2)可以使航天器某方向对太阳定向,保障整星能源,择机转回正常运行模式;3)可以直接转回正常运行模式.
以往航天器全姿态捕获控制过程一般采用喷气推进系统作为执行机构,采用基于陀螺、太阳敏感器和红外地球敏感器的“太阳-地球捕获”或“地球-太阳捕获”的全姿态捕获方式[2]实现对地定向卫星的姿态捕获.近年来随着磁强计和小卫星技术的发展,很多学者开展了利用磁力矩器和磁强计的磁控捕获研究.耿云海等[3]设计了一种利用磁力矩器控制的磁偶极子算法应用于重力梯度小卫星的入轨姿态捕获.孙兆伟等[4]针对小卫星入轨阶段的姿态捕获控制,提出了一种使用磁力矩器和反作用飞轮进行联合控制的算法,由磁强计测量的地磁场强度矢量、陀螺测量的卫星角速度设计磁力矩器控制的磁矩向量算法,磁阻尼完成后同时引入动量轮和太阳敏感器实现对日捕获控制.刘海颖等[5]针对非重力梯度稳定、偏置动量轮加三轴磁控的微小卫星初始姿态控制阶段,采用B-dot控制进行速率阻尼,设计了滑模控制律进行姿态捕获.钱山等[6]针对纯磁控微小卫星姿态捕获问题,提出了一种基于姿态角和姿态角速度反馈的磁矩能量控制律.上述方法存在如下不足:1)仅考虑了单独对地或对日捕获;2)采用推进系统或磁力矩器进行姿态捕获,消耗燃料或捕获速度慢;3)采用太阳敏感器,存在地影区不能见太阳的问题;4)采用磁强计,不仅增加了硬件配置,而且需要考虑磁强计和磁力矩器的分时工作问题.
当前卫星大多配置了动量轮和星敏感器,星敏感器的动态性能和全天球捕获能力越来越高,本文给出一种基于动量轮的全姿态捕获方法,并给出了在轨验证结果.
1 基于动量轮的全姿态捕获
基于动量轮控制的全姿态捕获主要包括如下步骤:1)速率阻尼;2)恒星捕获;3)姿态更新和星本体地磁强度计算;4)太阳定向姿态确定;5)目标捕获姿态确定;6)轮控调姿和磁力矩器卸载.流程图见图1.涉及的执行机构只有动量轮和磁力矩器,敏感器只有陀螺和星敏感器,都是属于卫星的常规配置.

图1 基于动量轮的全姿态捕获流程图Fig.1 Flow chart of GAA based on reaction wheel
1.1 速率阻尼
本步骤目标:通过动量轮控制,减小卫星姿态角速度,为恒星捕获提供条件.
根据陀螺测量数据预估姿态和角速度,以欧拉角表示姿态为例,算法如下:

式中,ωx、ωy、ωz为陀螺测量的星体三轴惯性角速度,φ、θ、ψ和为预估的星体三轴姿态角和角速度,Δt为采样周期.
动量轮作为执行机构,采用PD控制律,将卫星角速度阻尼到所确定的阈值.阈值的选取要考虑两个方面:1)将星体角速度阻尼下来;2)为恒星捕获提供条件,以满足星敏感器的全天区捕获功能对星体角速度大小的要求.一般取0.1 ~0.3(°)/s.
1.2 恒星捕获
本步骤目标:通过动量轮转动星体,直至星敏感器输出有效数据.
速率阻尼完成一定时间后,一定时间指大于星敏感器全天区捕获时间指标,判断星敏感器数据,如果星敏感器没有识别出有效恒星,则转动星体一定角度(一般至少大于2倍星敏感器视场范围)以改变搜索天区(例如每次转动先绕某轴转动45°,该轴完成一周天转动后,再绕另外一轴转动90°,如此反复),再判断星敏感器数据,直至完成恒星捕获,获得初始姿态.
此过程与速率阻尼一样,根据陀螺测量数据预估姿态和角速度,动量轮作为执行机构,采用PD控制律,PD控制律的选取要考虑轮控作用后,动量轮不超过允许的角动量范围并有一定的余量(如10%).
通过角度限幅,可以限制星体转动角速度,避免动量轮饱和,以转动星体某轴为例,假设角度限幅值为 θf,轮控PD 控制参数分别为kp、kd(kp、kd分别代表PD控制律的比例、微分参数),则星体转动角
1.3 姿态更新和星本体地磁强度计算
恒星捕获完成后,如果星敏感器数据有效,则根据双矢量几何定姿原理,由星敏感器数据直接更新卫星姿态;如果星敏感器数据无效,则根据陀螺测量数据预估姿态[7-8];根据卫星姿态和轨道,采用地磁强度拟合算法计算航天器本体地磁强度.
如果星敏感器数据有效,则姿态更新算法如下(以单星敏感器A有效为例):
1)如果星敏感器输出数据为四元数,则

2)如果星敏感器输出数据为测量轴矢量,则

3)计算本体系相对轨道系的姿态矩阵

4)将姿态矩阵CBI转换为姿态四元数并赋给q.式中,qmA、ZAI和XAI分别为星敏感器输出的四元数、光轴和横轴矢量,ZAB、XAB、YAB分别为星敏感器光轴、横轴、Y轴在星体系方位的单位列矢量,CBI为本体系相对惯性系的姿态矩阵,CBO为本体系相对轨道系的姿态矩阵,COI为轨道系相对惯性系的转换矩阵,函数Aq(·)为将四元数化为姿态矩阵的通用公式,q为本体系相对惯性系的姿态四元数(q=[q1q2q3q4]T).
如果星敏感器数据无效,则根据陀螺测量数据预估姿态四元数,算法如下:

式中,ω=[ωxωyωz]T,函数 Eq(·)为计算姿态四元数运动的通用公式,函数Fn(·)是计算归一化四元数且四元数标量小于零时将四元数均反号.
根据轨道信息,采用四阶以上地磁强度拟合算法计算得到在卫星轨道系下的地磁强度BO,则在卫星本体系下的地磁强度矢量BB为:

1.4 太阳定向姿态确定
本步骤目标:根据卫星姿态、轨道和太阳星历确定太阳方位.
以太阳在卫星-Z面入射为例定义太阳方位极性,两个极性箭头分别与星体+X、-Y方向一致,从箭头尾部向头部看去,太阳从左面入射,输出为正,根据卫星姿态、轨道和太阳星历确定太阳方位的算法为:

式中,Sb=[SbxSbySbz]T为太阳矢量在星体系的单位矢量,Si为太阳矢量在惯性系的单位矢量,αφ和αθ为太阳方位的计算值.
1.5 目标捕获姿态确定
本步骤目标:根据空间捕获目标、姿态和轨道信息,确定星体相对目标的姿态和角速度.
星体相对目标的姿态四元数qBT的计算公式为

星体相对目标的姿态角速度ωBT的计算公式为

式 中,qBT=[qBT1qBT2qBT3qBT4]T,ωBT=[ωBTxωBTyωBTz]T,qTi为目标相对惯性系的姿态四元数,ωTi为目标在惯性系的期望姿态角速度.特别地,捕获目标为对地定向零姿态飞行时,目标即轨道系,qTi为轨道系相对惯性系的姿态转换四元数,,ω0为卫星轨道角速度,这样姿态确定算法可以进一步简化.
1.6 轮控调姿和磁力矩器卸载
本步骤目标:采用动量轮作为执行机构,完成太阳定向或目标捕获.
采用PD控制律,通过角度限幅限制星体转动角速度,避免动量轮饱和.利用星敏感器获得有效初始姿态后,采用磁力矩器进行动量轮卸载,提高动量轮吸收角动量的能力,在地磁强度和角动量偏差矢量的夹角范围内(如45°~135°),角动量偏差至少大于2倍动量轮角动量测量误差,才进行磁卸载,以防止误卸载.PD控制律的选取要考虑两种情况:1)尽量确保星体角速度在一定范围内,以利于星敏感器工作于跟踪模式;2)轮控作用后,动量轮不超过允许的角动量范围并有一定的余量(如10%).相关算法如下.
1)太阳定向控制算法(以星体-Z面对日为例)
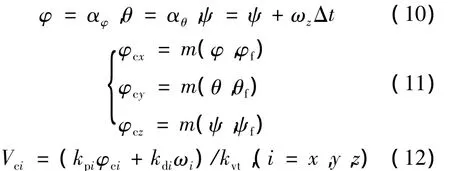
式中,φf、θf和ψf为姿态角限幅值,kvt为动量轮力矩电压系数,Vci为动量轮控制电压(i=x,y,z),kpi和kdi分别为PD控制律的比例、微分参数.函数m(*,·)为限幅函数,定义如下:

2)目标捕获控制算法

2 在轨验证情况
某卫星丢失姿态后,采用上述方法进行了全姿态捕获,执行机构为3个正交的动量轮,卫星依次经历了速率阻尼、恒星捕获、建立对地定向姿态等,卫星获得有效双矢量定姿姿态后,采用磁力矩器对动量轮卸载,姿态和角速度曲线见图2~4(说明:角度有限幅),可见采用该方法能够有效实现全姿态捕获,不消耗燃料,而且实现简单.

图2 姿态角曲线Fig.2 Attitude angles

图3 姿态角速度曲线Fig.3 Attitude angle velocities

图4 动量轮转速曲线Fig.4 Rotating speeds of reaction wheel
3 结论
本文给出了一种基于动量轮的全姿态捕获方法,包括步骤、姿态确定方法和控制算法等,采用的部件为动量轮、磁力矩器、陀螺、星敏感器等,都属于卫星的常规配置,可以实现对太阳、地球或其他任意目标定向,该方法实现简单、可操作性强、不消耗燃料.在轨验证结果表明该方法有效、工程可操作性强.该方法为航天器安全模式设计提供了一种行之有效的手段,并在后续卫星中得到了广泛应用.
4 致谢
在技术研究和在轨试验过程中,许多领导、专家和同事,如张笃周、袁利、徐福祥、何英姿、魏春岭、周剑敏、赵性颂、雷拥军、王淑一、田科丰等,提出了许多有价值的思路和建议,在此一并致以衷心的感谢.
[1]MAK T.A study of on-orbit spacecraft failures[J].Acta Astronautica,2009,64(2):195-205.
[2]屠善澄.卫星姿态动力学与控制[M].北京:宇航出版社,2001:513-517.
[3]耿云海,崔祜涛,孙兆伟,等.小卫星主动磁控制地球捕获姿态控制系统设计[J].航空学报,2000,21(2):142-145.GENG Y H,CUI H T,SUN Z W,et al.Attitude control system design for small satellite earth acquisition with active magnetic control[J].Acta Aeronautica and Astronautica Sinica,2000,21(2):142-145.
[4]孙兆伟,杨旭,杨涤.小卫星磁力矩器与反作用飞轮联合控制算法研究[J].控制理论与应用,2002,19(2):173-177.SUN Z W,YANG X,YANG D.The combined control algorithm for magnetorquer and reaction wheel of small satellite[J].Control Theory & Applications,2002,19(2):173-177.
[5]刘海颖,王惠南,陈志明.磁控微小卫星速率阻尼和姿态捕获研究[J].宇航学报,2007,28(2):333-337.LIU H Y,WANG H N,CHEN Z M.Detumbling controller and attitude acquisition for micro-satellite based on magnetic torque [J].Journal of Astronautics,2007,28(2):333-337.
[6]钱山,张士峰,蔡洪.纯磁控微小卫星的姿态捕获控制研究[J].宇航学报,2011,32(1):72-80.QIAN S,ZHANG S F,CAI H.Study on attitude acquisition of micro-satellite with only magnetic actuators[J].Journal of Astronautics,2011,32(1):72-80.
[7]章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998:212-213.
[8]刘一武,陈义庆.星敏感器测量模型及其在卫星姿态确定系统中的应用[J].宇航学报,2003,24(2):162-167.LIU Y W,CHEN Y Q.Star-sensor measurement model and its application to the spacecraft attitude determination system [J].Journal of Astronautics,2003,24(2):162-167.

