飞轮扰振特性及振动控制方法*

张激扬，刘 虎，王 虹，罗睿智，陈宗基

(1.北京控制工程研究所，北京，100190;2.北京航空航天大学，北京100191)

0 引言

航天器在轨工作时，以飞轮为代表的角动量交换型执行机构，由于自身存在静、动不平衡，会在工作时输出不期望的振动力和振动力矩(通称扰振)，使航天器平台发生轻微的抖动，这种抖动会影响有效载荷性能.因而飞轮类旋转执行机构在工作时产生的扰振，被普遍认为是影响有效载荷成像质量和指向精度的主要因素之一［1-3］.消除飞轮等旋转执行机构扰振对有效载荷的性能影响，是航天器高精度稳定平台的关键技术.

在航天器平台中，扰振对载荷的影响有三个要素:振动源(飞轮等执行机构)、振动传递路径(舱板、承力筒等)、敏感点(光学相机等高精度载荷).当前，中国高精度稳定平台解决扰振问题的主要措施是在振动传递路径上进行振动抑制和隔离［4-5］.这种方式虽然在一定程度上可以缓解扰振的影响，但也存在相应的局限:一是缺乏通用性，必须针对不同的航天器平台以及不同的安装位置开展振动隔离设计，在实现隔振目的的同时必须确保对振动源其他特性的影响处于可控范围内;二是效果难以验证，由于无法消除的重力影响，使得在轨振动隔离效果难以在地面有效验证.

因此，对扰振源开展振动抑制研究并采取相对独立于应用平台的振动抑制措施，是一种更为理想的技术途径.由于振动源具有振动机理复杂、振动特征多样、振动耦合因素多等特点，因此需要针对扰振源进行振动机理分析，掌握其振动特征，并在此基础上开展振动抑制方案研究，实现在源头大幅降低振动力并满足应用要求的目标.

本文分别针对机械飞轮和磁悬浮飞轮这两种空间应用典型执行机构产品，介绍现阶段在振动抑制和振动控制方面的研究情况.

1 机械飞轮振动控制

1.1 机械飞轮结构及其扰振模型

机械飞轮的外形如图1(a)所示，其内部结构简图如图1(b)所示.其主要由轮体、滚动轴承组件、电机和壳体等构成;在工作时，轮体、电机转子和轴承安装壳等零部件构成一个高速旋转体.针对飞轮的结构本质，其振动主要包括飞轮内部的振源激励和飞轮结构的振动传递，飞轮的振源因素较为复杂，但主要振源包含两部分:静、动不平衡量所产生的离心力和力偶及预紧轴承各相关部件工作面的几何误差所导致的预紧力的波动，其合成可分解为径向的激振力f(t)=fx(t)i+fz(t)k和激振力矩g(t)=gx(t)i+gz(t)k.建立飞轮结构的动力学模型［6］，并在此基础上分析振动传递函数，可以帮助深入理解机械飞轮扰振的本质并对其进行定量研究.

由于飞轮主要绕转轴旋转，径向转角θox和θoz都非常小，因此可根据陀螺力学和分析力学的理论建立飞轮旋转体沿径向平动和绕径向转动的动力学方程分别为

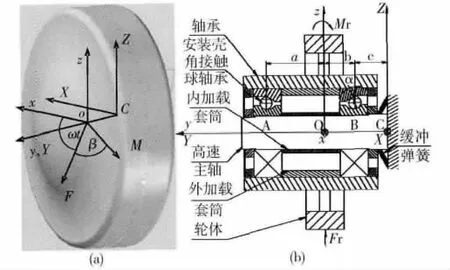
图1 飞轮的结构示意图及其坐标系Fig.1 Structure scheme of a flywheel and its coordinate system

式中:Kfrx，Kfrz分别为转子中心在x，z方向有单位位移时施加于o点的沿x，z方向的力;Kfθx，Kfθz分别为转子绕ox，oz轴有单位转角时施加于o点的沿z，x方向的力;Kmθx，Kmθz分别为转子绕ox，oz轴有单位转角时施加的对ox，oz轴的力矩;Kmυx，Kmυz分别为转子在z，x方向产生单位位移时，施加的对ox，oz轴的力矩;和分别表示相应的阻尼力和力矩.根据两坐标系的关系可得到旋转体基座上的振动力和力矩:

对式(1)～式(3)进行Laplace变换.即可得到基座上输出的径向振动力和力矩Fst(s)=［FstX(s)，FstZ(s)，GstX(s)，GstZ(s)］与质心处振动激励力和力矩 Ffg(s)=［fx(s)，fz(s)gx(s)，gz(s)］之间的函数关系:Fst(s)=TH(s)Ffg(s).这就建立了飞轮的不平衡量和轴承几何误差导致的预紧力波动量的激励与飞轮基座上的振动输出间的函数关系.

根据某规格飞轮的结构参数和微振动特征，在不平衡量和轴承的几何误差激励下，按照上述关系式仿真得到飞轮基座上输出振动力的瀑布图(频率-转速-振动力)如图2(a)所示，利用多分量测力台实测飞轮径向振动瀑布图如图2(b)所示.经对比分析，两个谱图在频率成分、涡动频率曲线形式和振幅的变化趋势等方面基本吻合，表明对影响飞轮振动特性的关键因素把握准确、理论分析正确.

图2 某规格飞轮径向(X)振动力瀑布图及其固有频率曲线Fig.2 Waterfall plots of vibration force and its natural frequency for a flywheel in the radial direction(X)

1.2 机械飞轮被动振动控制设计

基于上述分析可知，影响机械飞轮微振动特性的主要因素是其静、动不平衡量以及轴承的几何误差.理论上有效控制并降低这两个因素，就可以从根源上解决机械飞轮扰振问题.但实际飞轮转子并非理想刚体且存在结构连接环节，轴系的几何误差进一步减小的空间十分有限，同时在力学及环境应力作用下还会使初始调整状态发生变化，这些影响因素现阶段都难以有效消除.因此对机械飞轮产生的无法避免的微振动进行有效的振动控制是更为可行的措施.

机械振动控制通常分为被动控制与主动控制两类，被动振动控制方法简单易行，但对一些问题其控制效果有限;主动振动控制针对某些应用可以取得更好的控制效果，但相关技术较为复杂.被动控制相当于开环控制;而主动控制是闭环控制，即在振动控制过程中，根据所检测到的振动信号，应用一定的控制策略驱动作动器，从而达到抑制或消除振动的目的［7］.高精度稳定卫星平台要求飞轮扰振既不能影响姿态控制精度，又不能影响成像精度，因此对飞轮振动控制设计的主要意图是将相关频率下的扰振力抑制到较低量级.尽管主动振动控制技术不失为解决机械飞轮振动的有效途径，但能够实现上述振动控制意图的更为简便可靠的被动振动控制技术应该是空间机械飞轮首选的技术途径.针对飞轮宽频段微振动特点，以及需要承受主动段强力学环境和较高的角动量矢量精度要求，需要有效解决被动控制器宽频抑制与组合体结构高刚度的耦合设计问题(本文仅对机械飞轮被动控制器的宽频抑制设计进行说明).

为方便分析，机械飞轮在振动控制器上的运动可以简化为6个解耦的单自由度运动，其单自由度基本模型如图3所示.其中，m0、x0分别为飞轮质量与位移，k0、c0分别为振动控制器的刚度系数与阻尼系数，p(t)为飞轮内部周期性激励载荷，f(t)为传递到卫星结构上的作用力.

图3 单自由度被动振动控制器基本模型Fig.3 Schematic diagram of the SDOF passive vibration isolator

根据该简化模型，可以建立系统的动力学方程

传递到卫星安装表面的作用力为

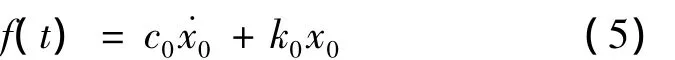
对上两式作Laplace变换，得到p(t)至f(t)的传递函数

令s=jω得到载荷传递率

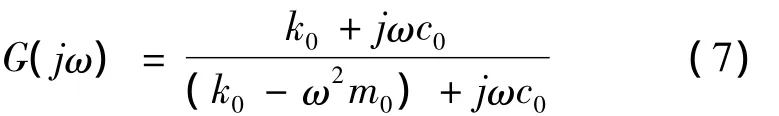
固有频率与阻尼比分别为

传递率可写作

根据卫星应用需求以及机械飞轮的技术特点提出相应的扰动力传递率设计要求.基于以上数学模型，初步确定机械飞轮被动振动控制器的几何构型，建立有限元模型，调整弹性元件的相应参数，计算飞轮-振动控制器系统的固有频率，直至满足设计要求.而后调整隔振装置中阻尼元件的阻尼比，计算系统的传递率，直至传递率和衰减系数满足设计要求.按照上述过程研制的被动振动控制器，不同阻尼比ζ0下的扰动力传递率设计仿真曲线如图4(a)所示，通过锤击法获得飞轮被动振动控制器的传递特性如图4(b)所示，实现情况与设计仿真基本吻合.

图4 扰振力传递函数曲线Fig.4 Transfer function curves of disturbance forces

1.3 机械飞轮被动振动控制效果

机械飞轮被动振动控制器性能验证工作在测力台上开展，图5是验证试验平台.定义垂直于台面方向为Z向，即飞轮角动量H矢量方向;与测力台平行的两个方向分别为X向和Y向.考虑到飞轮静、动不平衡量对X向及Y向振动力的影响更为显著，且由于其旋转轴对称设计的结构特点决定了X向及Y向微振动特性基本一致，因此可以X向振动力在振动控制前后的变化情况为代表，对飞轮被动振动控制效果进行分析.

图5 飞轮被动振动控制器验证平台Fig.5 Performance verification of the flywheel passive vibration isolation

图6给出机械飞轮在振动控制前后升速过程的三维瀑布图.从图中可见，在卫星平台较为关注的5～100 Hz频率范围内，整个升速过程振动力的主频是飞轮工作转速频率.对该振动力进行被动振动隔离后，振动幅值大幅衰减，仅在15 Hz附近处存在小幅的耦合振动，这是振动控制器固有频率与飞轮工作频率耦合的结果，与图4所示的设计预期吻合.此外，采用振动控制后的飞轮工作频率对应峰值不再随转速升高呈非线性增大，而是在耦合振动后随转速提升呈逐渐衰减趋势，这符合该系统错频抑振的设计原则，也体现了优先保证飞轮常态工作转速范围内低扰振力的设计意图.同时对于100 Hz以上的涡动频率、结构固有频率、工作频率高次谐波及其相互耦合振动均实现了有效的振动抑制，振动幅值衰减率优于90%.对比验证结果表明，所设计的被动振动控制器对机械飞轮具有显著的振动抑制效果.

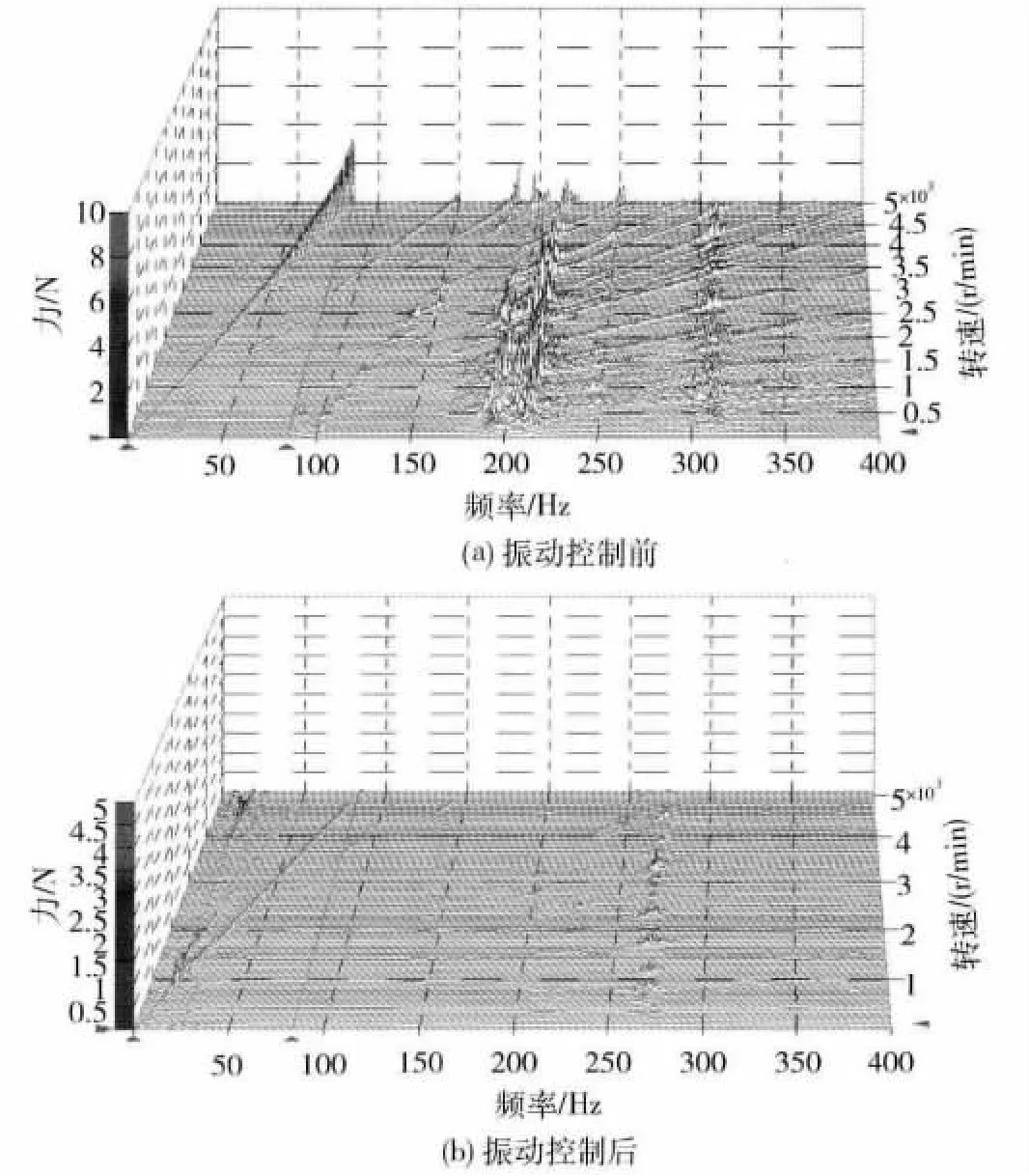
图6 机械飞轮实施振动控制前后升速过程扰振力瀑布图(0～400 Hz)Fig.6 Waterfall plots of disturbance forces for a mechanical flywheel before and after vibration isolation(0～400 Hz)

2 磁悬浮飞轮主动振动控制

磁悬浮飞轮无接触的支承方式为从根源上解决微振动问题开辟了新的途径，在航天器高精度稳定平台应用方面具有独特的发展潜力.

然而，由于存在固有的转子不平衡以及转子位移传感器误差、磁轴承的磁场不均匀性、功率放大器的输出非线性、驱动电机的偏拉力等非理想因素，如果不采取相应的振动控制措施，磁悬浮飞轮转动时仍然会导致旋转轴和惯性主轴存在偏差，产生扰动力和力矩［8］.磁悬浮飞轮主动振动控制就是通过调节作用在飞轮转子上的磁轴承力，在各种因素引起的扰动存在的工作条件下，使转子的转轴与惯性主轴在整个工作转速范围内相重合，实现低扰动力和力矩输出.

2.1 磁悬浮飞轮结构及其扰振模型

一种新型的五自由度全主动磁悬浮飞轮的结构如图7所示.与传统的双径向磁轴承、单轴向磁轴承配置方式不同，磁轴承系统由上、下两个轴向磁轴承和一个径向磁轴承组成.其中，轴向磁轴承产生转子轴向平动控制力和径向偏转控制力矩，而径向磁轴承只产生转子的径向平动控制力.支承其稳定悬浮的磁轴承及其功放驱动、传感器、控制器本身也构成了主动振动控制单元，因此可以不增加额外环节实现自身的主动振动控制.

图7 五自由度磁悬浮飞轮结构示意图Fig.7 Structure scheme of a magnetically suspended flywheel with 5-DOFs

由于磁悬浮飞轮的最高工作转速远低于转子的一阶弯曲模态频率，因此在对其进行动力学分析时可将转子视为刚性转子.除转子的转动自由度外，其余五个自由度的运动由磁轴承控制.根据陀螺力学理论，磁悬浮飞轮转子的动力学方程可写为

式(9)为转子径向平动自由度的动力学方程，式(10)为转子轴向平动与径向扭转自由度的动力学方程.式中:qr=［xy］T，qa=［β-αz］T;Mr=diag{m，m}，Ma=diag{Jr，Jr，m};Fr=［fxfy］T，Fa=［py-pxfz］T;Ga为陀螺矩阵.x、y和z为转子的平动位移;α和β为转子的扭转位移;m为转子的质量，Jr和Jp分别为转子的赤道转动惯量和极转动惯量;Ω为飞轮的自转角速度;fx、fy和fz为磁轴承的平动控制力，px和py为磁轴承的扭转控制力矩.

假设转子在平衡点附近小范围运动，磁轴承产生的控制力可线性化表示为:

式(12)和式(13)中:ksx、ksy和ksz为磁轴承的平动位移负刚度，ksα和ksβ为磁轴承的扭转位移负刚度;kix、kiy和kiz为磁轴承的平动电流刚度，kiα和kiβ为磁轴承的扭转电流刚度;Θx、Θy、Θα和Θβ为不平衡引入的扰动项;εx、εy、εα、εβ为传感器误差引入的倍频扰动项.不平衡扰动项和传感器倍频扰动项具有如下形式:

令 ksr=diag{ksx，ksy}，ksa=diag{ksβ，ksα，ksz};kir=diag{kix，kiy}，kia=diag{kiβ，kiα，kiz};ir=［ixiy］T，ia=［iβiαiz］T;Θr=［ΘxΘy］T，Θa=［ΘβΘα］T; εr=［εxεy］T， εa=［εβεαεz］T.转子的动力学方程可表示为以下矩阵形式:

由式(18)和(19)可知，由于不平衡扰动项Θr和Θa以及传感器偏差扰动项εr和εa的存在，磁轴承转子的动力学方程中会产生同频和倍频分量.

2.2 磁悬浮飞轮主动振动控制设计

磁悬浮飞轮磁轴承系统闭环回路如图8所示，主要由控制器、功率放大器以及磁轴承-转子系统组成，其传递函数矩阵分别为 Gc(s)、Ga(s)和P(s).磁轴承振动主动控制的目标就是在存在不平衡扰动和传感器误差的条件下，通过设计控制器Gc(s)实现转子绕惯性主轴旋转.

图8 磁轴承闭环系统示意图Fig.8 The closed-loop system of Magnetic bearings

因此磁悬浮飞轮主动振动，必须抑制静、动不平衡和传感器误差引起的扰动，采用图9所示的主动振动控制方法.

图9 磁悬浮飞轮主动振动控制方法框图Fig.9 Active vibration control diagram of magnetically suspended flywheels

图9中，Nf和Ns均为通用陷波器，两者的不同之处在于Nf的中心频率与转子的转频同步，而Ns的中心频率为转频的i倍.闭环反馈系统收敛后Nf的输出即为位移信号中的同频分量，而Ns的输出为位移信号中的倍频分量，通过Nf和Ns可分别实现转子位移信号中不同频率分量的分离.由于同频分量由转子的不平衡引起，经过位移负刚度的补偿，即可消除转子振动频谱中的同频分量［9］.而对于传感器误差引起的倍频分量，由于其并非转子的实际位移，因此不需要进行负刚度补偿.图中:μ为反馈系数，决定了通用陷波器Nf和Ns的收敛速度和中心陷波器的带宽;σ∈{0，1}为开关函数，如果σ=1则振动控制算法工作在闭环状态，反之如果σ=0，则振动控制算法切换至开环工作状态;θ1和θi为保证全转速范围稳定引入的相位调整角;i为倍频信号的阶次，对于传感器误差引起的每个倍频信号，需要设置独立的Ns，因此需要多次进行Ns叠加，只要选择合适的反馈系数μ和相位调整角θ1及θi，理论上即可保证全转速范围内闭环控制算法的收敛.

2.3 磁悬浮飞轮主动振动控制效果

磁悬浮飞轮主动振动控制性能验证工作同样在如图5所示的测力台上开展，测试过程中，磁悬浮飞轮固定在安装基座上，安装基座与振动测试台相连.

图10为未加控制情况下磁悬浮飞轮振动力的瀑布图，从图中的测试结果可知:未进行主动振动控制前，同频扰动力为磁悬浮飞轮振动力的主要成分，并随转速的升高而增大.除同频扰动力外，磁悬浮飞轮扰动力瀑布图中还存在着多个倍频振动力分量.图11为加入同频主动振动控制算法时的振动力瀑布图，采用消除线圈同频电流并对位移负刚度进行补偿的方法同频振动力有效衰减了90%以上.图12为增加倍频陷波器Ns后的振动力瀑布图，从图中可知，通过增加2倍频、3倍频和5倍频陷波，相应的分量在整个转速范围内均得到有效衰减，最大衰减超过80%.测试验证情况表明，本文所采用的方法可以有效降低磁悬浮飞轮扰振力.

图10 磁悬浮飞轮无振动控制声速过程扰振力瀑布图Fig.10 Waterfall plot of the disturbance force for a magnetically suspended flywheel without vibration control

图11 磁悬浮飞轮同频陷波及位移负刚度补偿控制后扰振力瀑布图Fig.11 Waterfall plot of the disturbance force for a magnetically suspended flywheel with synchronous frequency notch filtering and displacement negative stiffness compensation control

图12 磁悬浮飞轮同频及多倍频陷波扰振力瀑布图Fig.12 Waterfall plot of the disturbance force for a magnetically suspended flywheel with synchronous and multi-frequency notch filtering

3 结论

本文分析了机械飞轮及磁悬浮飞轮两种具有代表性的角动量交换型执行机构产品的扰振特性，在建立各自扰振模型的基础上，分别阐述了其被动振动控制和主动振动控制方法，并验证了方法的有效性.验证结果表明，不论是机械飞轮还是磁悬浮飞轮均可以通过采取适当的振动控制措施在较宽频段内显著降低其扰振力.相应振动控制措施由于同产品设计、工艺特性紧密结合形成一体，达到了较为理想的从源头控制扰振力的目的，因此其振动控制效果具有不依赖于卫星平台的特点，可以满足多种平台的应用需求.相比而言，机械飞轮被动振动控制具有简单、可靠的特点;磁悬浮飞轮主动振动控制可针对特定频率抑制需求在轨灵活调整，具有广阔的应用发展前景.

［1］Liu K.C.，Maghami P.，Blaurock C..Reaction wheel disturbance modeling，jitter analysis， and validation tests for solar dynamics observatory［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，2008:1-18.

［2］JIN L，XU S J.Underactuated spacecraft angular velocity stabilization and three-axis attitude stabilization using two single gimbal control moment gyros［J］.Acta Mechanica Sinica，2010，26(2):279-288.

［3］ZHANG J R，RACHID A，ZHANG Y.Attitude control for part actuator failure of agile small satellite［J］.Acta Mechanica Sinica，2008，24(4):463-468.

［4］刘天雄，范本尧，杨慧.卫星飞轮扰振控制技术研究［J］.航天器工程，2009，18(1):53-60.LIU T X，FAN B Y，YANG H.Research on vibration disturbance control of momentum wheel［J］.Spacecraft Engineering，2009，18(1):53-60.

［5］罗敏，王耀兵.航天器微振动被动抑制技术综述［C］.全国振动工程及应用学术会议论文集.南京:中国振动工程学会，2012:91-95.LUO M，WANG Y B.Nanjing:Chinese Society for Vibration Engineering，2012:91-95.

［6］罗睿智，虎刚，王全武.悬臂式SGCMG的高速转子的径向振动特性研究［J］.振动与冲击，2014，33(5):200-204.LUO R Z，HU G，WANG Q W.Radial vibration characteristics of a high-speed rotor of a cantilevered SGCMG［J］.Journal of Vibration and Shock，2014，33(5):200-204.

［7］王加春，李旦，董申.机械振动主动控制技术的研究现状和发展综述［J］.机械强度，2001，23(2):156-160.WANG J C，LI D，DONG S.Review of mechanical active vibration control technique［J］.Jouranal of Mechanical Strength，2001，23(2):156-160.

［8］房建成，孙津济，樊亚洪.磁悬浮惯性动量轮技术［M］.北京:国防工业出版社，2012:405-410.

［9］LICHUAN L，TADAHIKO S，XIAO Y Z，et al.A simple method for rotation about the inertial axis of a rigid AMB rotor［C］.Proceedings of the 8thInternational Symposium on Magnetic Bearings.Japan:Mito，2002:405-410.