空间非合作目标的逼近控制仿真研究*

张 鑫，张雅声，姚 红

(装备学院，北京101416)

0 引言

人类自古就有飞上太空探索宇宙的梦想，据统计，从前苏联1957年10月4日将第一颗人造卫星发射进入太空以来，到目前为止，人类已经发射了超过上千颗卫星.其中一部分卫星因为自身的故障、失效或者寿命截止而停留在轨道上成为太空垃圾，不仅占用了稀缺的轨道资源，同时还会对其他的在轨航天器形成威胁［1］，甚至造成连锁的空间碎片效应，对空间环境形成严重污染.为了有效利用在轨航天器的资源或净化轨道环境，当前，世界各国正在研究以卫星维修、寿命延长和太空垃圾清除为目的的在轨操作服务技术［2］:包括对故障卫星进行绕飞监视、跟踪接近、交会对接和在轨维修等操作.比如美国的哈勃太空望远镜机器人修复计划、ESA的实验卫星服务计划(ESS)［3］以及日本的空间碎片清理卫星(SDMR)项目［4］等.总体上来讲，目前对于合作目标航天器的在轨服务技术当前已经比较成熟，但对于非合作目标，还存在较大的技术难题.

美国空间研究委员会、航空与空间工程局在哈勃太空望远镜修复计划的评估报告［5］中认为:非合作目标是指那些没有安装通讯应答机或其他主动传感器的空间目标，其他航天器不能通过电子讯问或发射信号等方式实现对此类目标的识别或定位.与合作目标不同，非合作目标既没有安装发光标志器或角反射镜作为目标识别的特征点，也不能利用星间链路来直接传输其位置和姿态信息［6］.所以，对非合作目标的接近捕获难度要远大于合作目标.对非合作翻滚目标的捕获策略主要有以下两种［7］:一种策略是保持服务航天器的位置和姿态，采用机械臂对目标航天器施加阻力，降低其转动角速度，然后进行捕获;另一种策略是控制服务航天器的位置和姿态，使服务航天器与目标航天器保持姿态同步，再进行捕获.前一种策略由于要施加阻力，对于翻滚目标来说存在较大的困难和风险;后一种策略通过与目标航天器保持姿态同步，具有较高的安全性以及更广阔的前景.文献［8］采用反馈控制和最优控制的方法，实现了服务航天器和目标航天器之间的姿态同步，这样有利于服务航天器上的机械臂抓取目标.文献［9］通过前馈和反馈的控制技术，实现服务航天器对目标航天器的姿态运动同步控制.文献［10］针对空间机器人捕获自由漂浮航天器的问题，设计了相对位置和姿态的同步控制算法.文献［11］中研究了服务航天器同自由翻滚的目标航天器近距离交会的最优控制问题.

服务航天器向目标航天器的跟踪接近过程是在轨服务中非常重要的一个过程.目前在轨服务的这些非合作对象基本上都处于GEO轨道上，其原因是GEO轨道资源有限，若以卫星间相隔1°计算，空间只有360个轨道资源，其中还包括了那些位于大洋上空的不太好用的轨道位置.文献［12］中对在轨航天器间的相对位置和姿态运动进行了初步的研究，但没有考虑逼近控制.本文在此基础上，建立了GEO轨道上服务航天器相对于姿态无控型非合作目标航天器逼近过程中全面的相对姿态和位置耦合运动方程，在假设位姿测量信息已知的前提下，采用PD控制律，设计了相应的Simulink模型并进行仿真研究.

1 逼近控制问题的描述

空间在轨服务的对象大部分是姿轨控失效的故障卫星或空间垃圾等姿态无控型目标，这类目标通常会绕着其最大惯量主轴进行自旋［13］，自旋角速度一般大于 1(°)/s［14］.对于这类目标捕获问题，服务航天器需要同时对目标的相对姿态和相对位置实行跟踪控制，使得最终捕获时的相对角速度为零，这样就要求在目标本体坐标系下沿着直线向捕获轴逐步逼近至抓捕点.

图1 服务航天器与目标航天器的相对位置关系Fig.1 Relative position relationship of the servicing spacecraft towards target spacecraft

如图1所示，各符号的定义分别为:

(1)x0y0z0-CM0表示目标航天器的本体坐标系，x1y1z1-CM1表示服务航天器的本体坐标系;

(4)ρ表示服务航天器质心相对于x0y0z0系的位置矢量;

(5)ρij表示服务航天器上的相对于目标航天器上的Pj0的位置矢量.

同时，假设目标以一定的角速度自旋.针对姿态无控型目标的最终逼近，需要使服务航天器保持对目标航天器的姿态跟踪，使ρij不断减小直至为零.由图1可以看出，矢量ρij不仅与相对质心位置ρ相关，还与航天器之间的相对姿态相关，也就是相对位置运动和相对姿态运动存在耦合影响.

2 相对运动数学模型

2.1 相对姿态动力学数学模型

假设服务航天器角速度为ω1，目标航天器角速度为ω0，则服务航天器与目标航天器之间的相对角速度为

在目标本体坐标系下，则式(1)可表示为

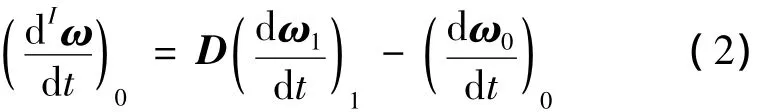
式中D为服务航天器本体坐标系到目标航天器本体坐标系的坐标转换矩阵.

又因为惯性系和目标系中相对角速度微分之间的关系为:

将式(2)代入式(3)中可得

另外目标航天器和服务航天器在各自体坐标系中的姿态动力学方程分别表示为

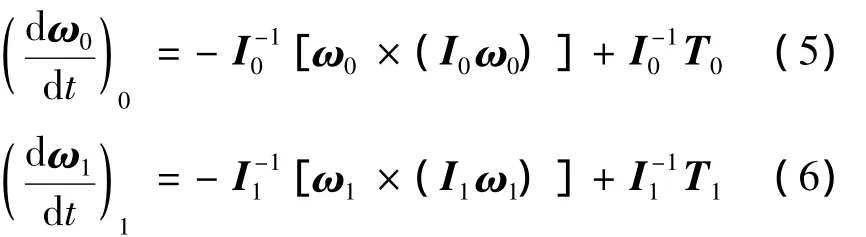
其中，I0，I1分别为各自的转动惯量，T0和T1分别为各自的控制力矩.

将式(5)和(6)代入式(4)中可得

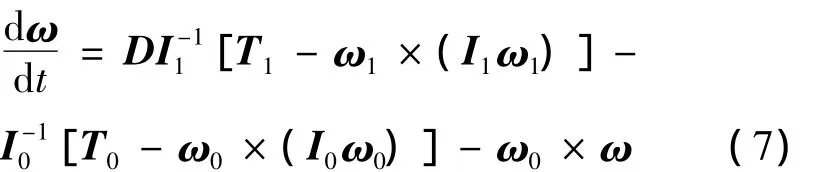
2.2 相对姿态运动学方程

姿态运动学方程用来描述航天器姿态与姿态角速度之间的相互关系.设目标航天器相对于服务航天器的转动角速度为 ω=［ωxωyωz］，则由四元数表示的姿态运动学方程为

其中

2.3 相对位置运动动力学模型

在目标本体坐标系中，图1中的矢量关系如下:

并且

所以式(10)化简可得

在目标的Hill坐标系中:

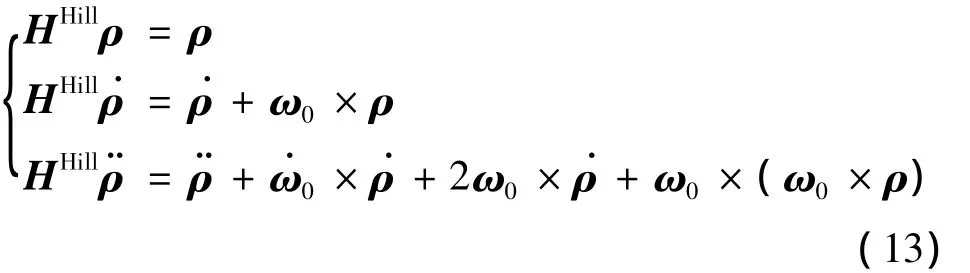
式中，H为目标Hill坐标系至目标本体坐标系的转换矩阵，Hillρ表示在Hill坐标系下服务航天器和目标航天器质心间的位置矢量.

联立式(12)和(13)可得

又可知在Hill坐标系下相对动力学方程为

其中

n为目标航天器轨道角速度.

将式(15)代入式(14)中，化简整理后可建立相对位置的状态方程如下:

2.4 姿态及位置跟踪比例-微分控制

假设相对姿态运动中的未知量都当做干扰力矩Td，则式(7)可化简为:

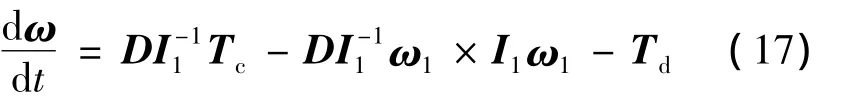
则相对姿态跟踪控制等效的比例-微分控制律设计为

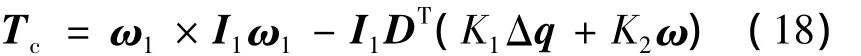
同理，当GEO轨道中的轨道角速度为小量时，通过相对位置指令设置服务航天器ρij点位置控制等效到其质心的位置控制(即=0)，则相对位置的动力学方程简化为

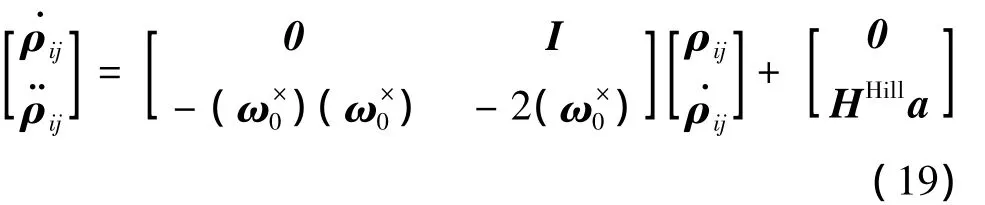
则相对位置跟踪控制等效的比例-微分控制律设计为

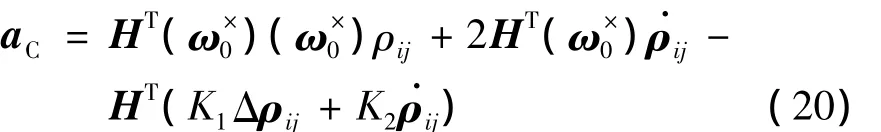
整个建模过程如图2所示.

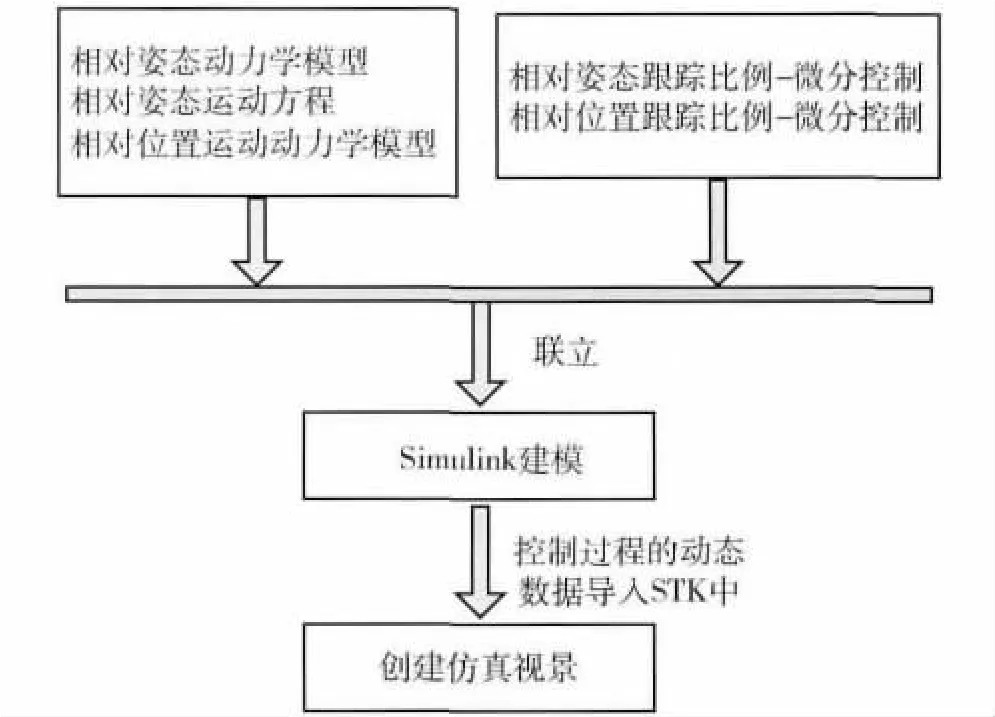
图2 建模流程Fig.2 Process of model building

3 仿真算例

假设服务航天器从目标航天器50 m以外采用闭环控制向目标航天器逼近，逼近相对速度为0.1 m/s，并保持自身姿态稳定，目标航天器自旋角速度为1(°)/s.仿真参数如表1所示

表1 仿真参数Tab.1 Simulation parameters

建立 Simulink仿真模型，仿真时间设置为500 s，仿真步长0.1 s，可得目标航天器的相对姿态变化曲线、相对角速度变化曲线、相对位置变化曲线、相对速度变化曲线、控制力矩变化曲线和控制加速度变化曲线，如图3～8所示.

由图3和图4可以看出，服务航天器和目标航天器之间的相对姿态和相对角速度在10 s左右就已经收敛为零，说明服务航天器很快就能够对目标航天器实现姿态跟踪;由图5可以看出，服务航天器和目标航天器的相对位置在500 s逼近至零左右，说明服务航天器最终实现了对服务航天器的抓捕;由图6可以看出，服务航天器和目标航天器的相对速度在40s左右已经逼近为0.1 m/s左右，说明服务航天器能够很好地对目标航天器实现位置跟踪.由图7和图8可以看出，随着服务航天器和目标航天器之间姿态的同步以及相对位置的减小，控制加速度从0.1 m/s2逐渐收敛到0.01 m/s2;控制力矩先从-1 N·m变为0.1 N·m，最后逐渐收敛为零.

图3 相对姿态曲线Fig.3 Relative attitude

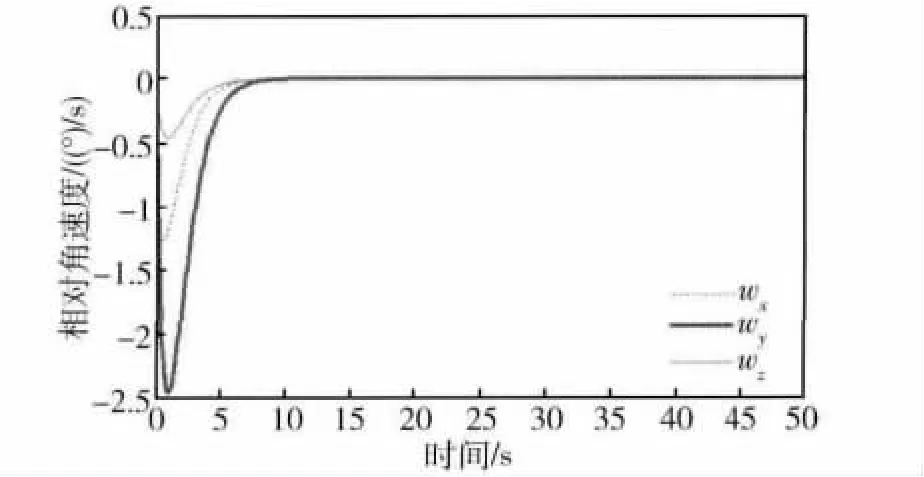
图4 相对角速度曲线Fig.4 Relative angular velocity

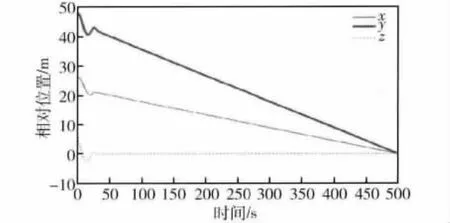
图5 相对位置曲线Fig.5 Relative position

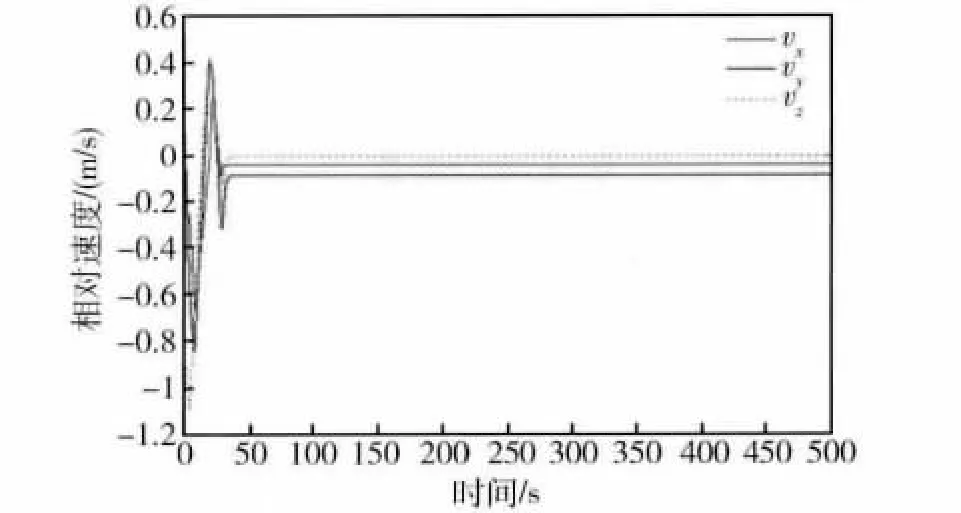
图6 相对速度曲线Fig.6 Relative velocity

图7 控制力矩变化曲线Fig.7 Control torque

图8 控制加速度变化曲线Fig.8 Control acceleration

将控制过程中的动态数据导入STK中，创建仿真视景如图9所示.

图9 STK仿真图Fig.9 STK simulation scene

图9中，目标航天器绕着V-bar自旋轴自旋，细虚线为固连于目标本体坐标系的捕获轴，也绕着目标自旋轴旋转，粗实线为服务航天器在目标Hill坐标系下的最终逼近轨迹.可以看出，目标在最终逼近过程中，服务航天器在目标本体坐标系下的轨迹是一条直线，在目标Hill坐标系下则呈现出一种环绕接近目标抓捕点的曲线.图9表明，服务航天器可以实现对于姿态无控型目标的跟踪逼近过程，本文所建立的相对位姿模型和设计的位姿联合跟踪控制方法正确有效.

4 结束语

由于GEO轨道资源的奇缺，未来针对非合作目标的在轨服务技术，包括目标识别、位姿测量和逼近捕获等将会成为研究的热点，这些技术将对空间垃圾清除和在轨废弃卫星资源利用起到重要作用.本文研究了针对非合作目标的在轨服务的逼近过程，建立了服务航天器向目标航天器跟踪逼近过程中的相对姿态运动模型和相对位置运动模型，选取经典的比例-微分控制方法，建立对应的Simulink仿真模型.根据最终的仿真结果分析得出:对服务航天器向目标航天器逼近过程中建立的相对姿态和位置运动模型正确有效，控制策略可行，能够满足对慢旋非合作目标航天器的近距离逼近捕获要求.

［1］徐文福，刘宇，梁斌，等.非合作航天器的相对位姿测量［J］.光学精密工程，2005，17(7):1570-1581.XU W F，LIU Y，LIANG B，et al.Measurement of relative poses between two non-cooperative spacecrafts［J］.Optics and Precision Engineering，2005，17(7):1570-1581.

［2］崔乃刚，王平，郭继峰，等.空间在轨服务技术发展综述［J］.宇航学报，2007，28(4):33-39.CUI N G，WANG P，GUO J F，et al.Development summary of space on-orbit servicing technology［J］.Journal of Astronautics，2007，28(4):33-39.

［3］HIRZINGER G，LANDZETTEL K，BRUNNERB，et al.DLR's robotics technologies for on-orbit servicing［J］.Anvanced Robotics，2004，18(2):139-174.

［4］NISHIDA S I，KAWAMOTO S，OKAWA Y，et al.Space deris removal system using a small satellite［J］.Acta Astronautica，2009，65(1-2):95-102.

［5］National Research Council.Assessment of Option for Extending the Life of the Hubble Spacetelescope:Final Report［M］.Washington:National Academies Press，2005:8-91.

［6］郝刚涛，杜小平.空间非合作目标位姿光学测量研究现状［J］.激光与光电子学进展，2013，1-9.HAO G T，DU X P.Advance in optical measurement of position and pose for space non-cooperative target［J］.Laser＆Optoelectronics Progress，2013，1-9.

［7］耿云海，卢伟，陈雪芹.在轨服务航天器对失控目标的姿态同步控制［J］.哈尔滨工业大学学报，2012，44(1):1-6.GENG Y H，LU W，CHEN X Q.Attitude synchronization control of on-orbit servicing spacecraft with respect to out-of-control target［J］.Journal of Harbin Institute of Technology，2012，44(1):1-6.

［8］NAKASUKA S，FUJIWARA T.New method of capturing tumbling object in space and its control aspects［C］//Proceedings of the 1999 IEEE International Conference on Control Applications.Piscataway:IEEE，1999:973-978.

［9］TSUDA Y，FUJIWARA T，NAKAMURAT，et al.The attitude control for motion synchronization to capture free-flying object［C］//Proceedings of the 8thISAS Workshop on Astrodynamics and Flight Mechanics.Tokyo:ISAS，1998:348-354.

［10］WELSH S J，SUBBARAO K.Adaptive synchronization and control of free flying robots for capture of dynamic free-floating spacecrafts［C］//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Reston:AIAA，2004:5298.

［11］BOYARKOG，YAKIMENKOD，ROMANOM.Formulation and analysis of matching points of interest in two spacecraft for optimal rendezvous［C］//AIAA Guidance，Navigation，and Control Conference.Reston:AIAA，2009:5669.

［12］KYLE T A，SRINIVAS R V，et al.Spacecraft formation flying dynamics，control and navigation［M］.Burlington:Elsevier Astrodynamics Series，2010:227-240.

［13］刘智勇，何英姿.慢旋非合作目标接近轨迹规划［J］.空间控制技术与应用，2010，12，36(6):6-10.LIU Z Y，HE Y Z.Slowly rotating non-cooperative target proximity trajectory planning［J］.Aerospace Control and Application，2010，12，36(6):6-10.

［14］MATSUMOTO S，DUBOWSKY S，JACOBSEN S，et al.Fly-by approach and guidance for uncontrolled rotating satellite capture［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Austin，Texas:AIAA，2003:5745.