轻轨隧道下穿建筑物爆破震动试验研究

王辉，阳生权，常中民，丁雄，赵磊军

（1. 湖南科技大学土木工程学院，湖南湘潭411201；2. 中铁十六局集团第三工程有限公司，湖州浙江313000）

轻轨隧道下穿建筑物爆破震动试验研究

王辉1，阳生权1，常中民2，丁雄1，赵磊军1

（1. 湖南科技大学土木工程学院，湖南湘潭411201；2. 中铁十六局集团第三工程有限公司，湖州浙江313000）

以重庆轨道交通环线体育公园站浅埋轻轨隧道工程为研究背景，进行了施工通道钻爆循环掘进下穿“两江春城”的爆破震动效应试验。在钻爆初期，通过监测参数计算出爆破振动衰减参数，并通过测量轻轨隧道下穿建筑物时，爆破引起的建筑物不同楼层处的振动速度波形，探讨建筑物的震动特性及爆破地震波传播和衰减规律。研究发现，其爆破振动衰减参数为=1.88，k=99.43；浅埋轻轨隧道钻爆掘进过程中，其垂直方向的爆破振速明显大于水平方向的，因此在研究爆破振动传播和衰减规律及其对建筑物振动的影响时，主要以垂直方向的爆破振速为依据；建筑物的爆破振速在底层随着楼层的增加而增大，中层随着楼层的增加而减小，顶层又随着楼层的增加而增大，而不是随楼层的增加而减小，即不满足传统萨道夫斯基衰减规律。同时测得轻轨隧道下穿建筑物后的爆破振速相比下穿前的，存在放大效应，其放大倍数约为1.32～1.69。

爆破震动；震动特性；衰减规律；放大效应；爆破振速

1 研究背景

随着我国城市化大发展、大繁荣，重庆市作为我国西南经济发展的中心，交通压力与日俱增。而重庆市有山城之名，属于岩基城市。钻爆法作为重庆市轻轨隧道循环掘进的主要方法，对加快重庆市的城市化建设，减缓城市交通压力有着举足轻重的作用。同时，重庆市地形高低起伏，特别是市内高楼众多，人口密集，轻轨站大都建在火车站、汽车站附近等人口密集处，有利于疏通交通要道。因此，爆破施工产生的爆破三大公害——空气冲击波、爆破飞石、爆破噪声，尤其是在城市复杂环境下爆破的地震效应，对建筑物的影响是不能忽视的[1-3]。以重庆市为代表的人口和建筑密集的岩基城市进行轻轨隧道循环爆破开挖，在设计时就对其爆破震动提出了严格的控制要求。因此在钻爆施工时，首先要求能够准确了解爆破地震波的传播和衰减规律，预测爆破振速，通过优化爆破设计与施工方案，使爆破振速在可控范围之内。

目前，我国在钻爆施工工程中通常采用萨道夫斯基公式预测爆破振速值[4-7]，即

式中：R为测点到爆破中心的距离，m；Q为炸药量，齐发爆破取总药量，微差爆破时取最大段装药量，kg；v为爆破岩石质点振动速度，cm/s；k为与岩石性质、爆破参数和爆破方法有关的场地系数；为爆破震动衰减系数。

对于爆破震动对建筑物的影响，有不少学者做了大量的研究，并取得了一些成果[8-12]。如朱振海等人[8]采用动光弹方法试验研究了沟槽对建筑物的减震作用，表明在建筑物附近开挖具有一定深度的沟槽对于降低爆破地震波对建筑物的危害具有明显效果，增加沟槽的宽度对于爆破地震波的传播影响不大；魏晓林[9]结合数个邻居建筑物实例的安全问题，进行了理论分析，提出了邻近建筑物大药量爆破危害的影响计算方法；王俊平等人[10]在研究爆破地震波作用下建筑物的动力响应分析方法时，首次将波动理论引入爆破工程中，为研究爆破工作开辟了一条新途径；张建波等人[11]采用回归分析的方法研究了浅埋隧道下穿建筑物的爆破振动传播规律，所得结论对类似工程有一定的借鉴意义；沈秀峰[1]运用有限元分析软件研究了爆破三要素——爆破地震波的幅值、频率、持续时间，对建筑物微振动的影响，得出了爆破地震波的特有性质；郭建群等人[12]提出了穿越高楼下的浅埋隧道爆破控制技术，认为在开挖断面积一定的条件下，存在一个较为合理的单循环进尺，其相应的炮孔数目最少，炸药单耗最低。

在已有学者研究的基础上，本文拟以重庆市轨道交通循环系中体育公园站施工通道下穿“两江春城”为研究对象，通过大量的实测数据，研究以此地区为代表的重庆岩基城市爆破地震的传播和衰减规律，以及建筑物不同楼层的爆破震动特性，以期为以后轻轨隧道采用钻爆法循环掘进施工方案提供一些参考性建议。

2 工程概况

重庆市轻轨隧道的体育公园站施工通道位于川东南弧形构造带，华蓥山帚状褶皱束东南部的次一级构造，构造骨架形成于燕山期晚期褶皱运动。

该工程的地质构造隶属于沙坪坝背斜西翼，岩层产状为：倾向290°，倾角5°。岩层面为贯通性结构面，层面之间的岩芯较为破碎，层间结合较差，为软弱结构面。该地属于构造剥蚀丘陵地貌，地面高程为301～307m，地表土层厚度为0.50～8.60m。该段施工通道全长412m，标准断面净宽6m，净高5.5m，埋深16～25 m，属于中浅埋隧道，采用钻爆法循环施工。该隧道围岩属于III、IV级，岩性以砂岩、泥质砂岩为主。

由于该施工通道下穿“两江春城”，且“两江春城”的部分主体结构还正在修建，钻爆法对其基础、地基、主体结构均会产生一定的影响，因此对其爆破振动控制要求较为严格。

3 监测方案与量测方法

重庆市轻轨隧道体育公园站的施工场地总平面图如图1所示。

图1 场地总平面图Fig.1The site layout

由于体育公园站施工通道下穿“两江春城”，新建建筑物众多，其中还包括刚施工完的地基基础，因此，在设计采用钻爆法施工时，对爆破振速提出了严格要求，其最大爆破振速要小于2cm/s。针对这一设计要求，在隧道爆破开挖初期，需要通过小炮试验，近距离爆心距跟踪监测。隧道开挖前期，在地表布置测点，爆破循环掘进进尺为2m，每次爆破完，地表测点推进2m，爆破监测测点布置见图2。

图2 钻爆初期爆破测点布置立面图Fig.2The elevation diagram for monitoring points layout in early drilling and blasting

通过实验，得出该地区的爆破震动传播和衰减规律，若不满足设计要求，则通过爆破设计进行优化，调整爆破参数。然后，在满足爆破设计确保建筑物安全的前提下，研究一栋具有代表性的7层框架结构楼房的不同楼层及地表在隧道下穿前后的爆破震动特性。此时采用远距离爆心距固定测点监测，即楼层及地表的监测点位置不变，随着隧道循环掘进，其爆心距不断变化。其爆破监测点布置如图3所示。

图3 下穿建筑物前后爆破测点布置立面图Fig.3The elevation diagram for monitoring points layout before and after undercrossing building

本次爆破震动监测，采用四川拓普测控科技有限公司生产的UBOX5016数据采集设备及配套软件进行数据采集。该振动测量系统由拾振器、记录仪和笔记本电脑组成，其爆破震动监测系统如图4所示。

图4 爆破震动监测系统Fig.4Blasting vibration monitoring system

现场爆破监测安装传感器时，采用适量的水与生石膏粉调节成浆糊状，将传感器粘结在石膏上，过几分钟后石膏凝固，使传感器与地面保持刚性连接，并且垂直速度传感器与水平面垂直，水平径向速度传感器与水平面平行，水平切向速度传感器在水平面内与水平径向速度传感器垂直，构成一个关于爆心的3维直角坐标系，进行爆破震动测试。

4 监测结果分析

为了严格按照设计控制标准，其最大爆破振速控制在2cm/s的范围内，施工方采用了边施工、边监测，同时优化爆破方案的信息化动态施工方法，有效地控制了爆破地震效应对周围密集的高层建筑的影响。在隧道钻爆初期，通过对爆破震动进行了监测，并计算出场地影响系数k的值和衰减指数值，了解此地区的爆破震动传播与衰减规律，其部分实验数据列于表1。

表1 钻爆初期施工爆破震动监测数据Table1The monitoring data of blasting vibration in early drilling and blasting construction

分析表1中的数据，在小炮实验中，其它条件变化不大的情况下，最大振速随着爆心距的增大而衰减，最大段用药量、爆心距、最大振速三者之间存在一定的函数关系。

运用UBOX5016和与之对应的开发软件BM BView，基于常用的萨道夫斯基公式（1）进行回归分析，对式（1）两边取对数，可得式（2）：

根据得出的爆破震动衰减公式，经试算，当单孔最大起爆用药量为8kg时，距离地表最近距离为16m的爆破振速为1.993cm/s，小于设计要求的2cm/s。因此，确定钻爆施工在保证安全的前提下，采用了最大单孔用药量为8kg。

随着钻爆施工的推进，对一栋具有代表性的7层框架结构楼房的不同楼层及地表在隧道下穿前后的爆破震动进行监测，由于篇幅原因，只列出部分数据，所得监测数据见表2。

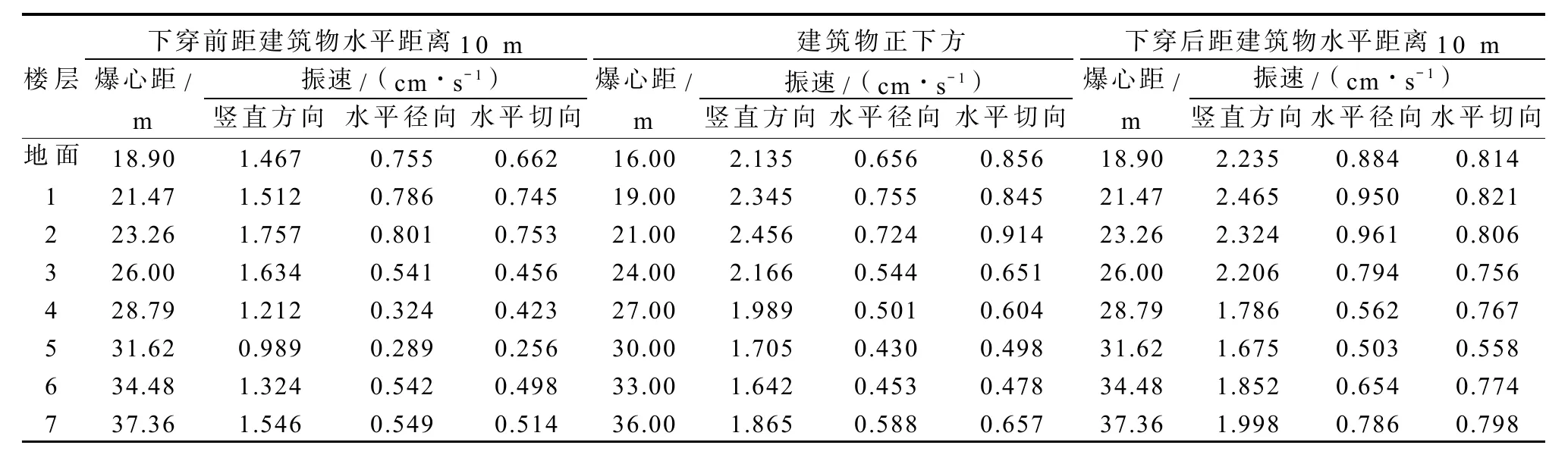
表2 下穿建筑物过程爆破震动监测数据Fig.2The monitoring data of blasting vibration during the process of undercrossing building

通过分析表2中的数据可以得出：首先，水平径向爆破振速、水平切向爆破振速明显要比垂直方向爆破振速小很多，因此，在分析爆破振动速度时，主要以垂直方向的爆破振速作为参考依据。同时，上述监测数据表明，垂直方向上的爆破振速已有部分超标，并没有达到预期效果。

当下穿建筑物前，其爆破振速基本在可控范围之内，当从建筑物正下方穿过时，开始存在爆破振速超标现象，如建筑物正下方爆心距16～24m处，竖直方向的振速均大于设计要求的2cm/s；甚至下穿后距建筑物水平距离10m，仍然存在爆破振速超标现象，如爆心距18.90～26.00m处，竖直方向的振速也均大于设计要求的2cm/s。

为了能准确地分析建筑物在爆破振动条件下不同楼层的震动规律，对建筑物不同楼层在轻轨隧道下穿前后的垂直方向爆破振速情况绘制了变化曲线，如图5所示。

图5 不同楼层垂直方向振动速度变化曲线图Fig.5The vibration velocity variation curves for the vertical direction of different floors

从图5中可以看出，建筑物的不同楼层在轻轨隧道下穿前后，其垂直方向爆破振速变化较大，3条垂直方向振动速度变化曲线都反映了爆破振速在底层时有随着楼层的增加而增大的变化趋势，然后在中层随着楼层的增加而递减，最后到顶层又随着楼层的增加而略微增大。这一变化趋势，打破了已有传统的爆破振动传播和衰减规律，即爆破振速并不是单纯地随着爆心距的增大而减少，需要考虑多方面的原因。因此，为了得出正确的爆破振动传播和衰减规律，本研究将实测建筑物正下方的爆破振速与根据已有衰减公式得出的预测爆破振速进行了对比，所得数据与误差分析结果具体见表3。

表3 理论预测与实测数据的比较及误差分析Table3Comparison of the predicting data and measured data and error analysis

分析表3中的数据可以得知，建筑物正下方的实测爆破振速与预测爆破振速相差甚远，其绝对误差、相对误差、放大倍数均相差较大。相比而言，最底层楼层的各数值相差较小，而最顶层的数值相差较大。同样，用回归分析的方法计算实测爆破振速的衰减规律，可得

其中，k=5.513，=0.398。

可以看出，该衰减方程不符合萨道夫斯基衰减规律。在低层时，实测爆破振速比预测振速大，有一个放大效应。唐海等人[13]也提出了爆破振动会随高程的增大而产生一个放大效应，在此次监测数据中得到很好的证明。当爆破振速传到中层时，爆破振速并不是一直增加的，而是在衰减系数的影响下减小，可以认为此时的衰减效应大于放大效应，会存在一个临界值。当爆破振动传到顶层时，爆破振速反而增加，并不是我们认为的爆破振动会衰减到更小，这主要是由于当爆破振动传到顶层时，顶层受到的自由约束最少。

由于下穿建筑物前后，在相同的爆心距情况下，爆破振速存在较大的差异，因此，对下穿建筑物前后不同楼层的爆破振速进行了对比分析，所得结果如表4所示。

分析表4中的数据可以得出，下穿建筑物后测得的不同楼层爆破振速明显比下穿前测得的爆破振速要大，同样存在一个放大效应，其放大倍数约为1.32～1.69倍。这主要是由于已开挖的隧道改变了原围岩的整体结构，浅埋轻轨隧道在爆破掘进过程中会产生“空洞效应”，从而导致爆破振动在下穿建筑物前后存在一个放大效应。

针对上述试验现象，通过对“两江春城”不同楼层的框架结构、砖混结构、框剪结构进行大量的爆破振动监测，发现均有类似规律：不同楼层的爆破振速，随着楼层的增加，先增大后减小，然后再增大；建筑物下穿后，相对于下穿前，爆破振速均有一个放大效应，且高层建筑相对于低层建筑，这一现象更为明显。

5 结论

1）在爆破施工初期，通过试验，并利用萨道夫斯基公式进行了回归分析，得出重庆轻轨隧道体育公园站地表振动衰减参数：=1.88，k=99.43，这一参数对此工程爆破施工具有一定的指导意义。

2）浅埋轻轨隧道钻爆掘进过程中，其垂直方向的爆破振速明显大于水平方向的爆破振速，因此在研究爆破振动传播和衰减规律，以及其对建筑物振动的影响时，主要以垂直方向的爆破振速为依据，但也不能忽略水平方向的爆破振动对建筑物的影响。

3）在考虑建筑物爆破振动的传播和衰减规律时，需要打破传统的观念，在本文研究的工程实例中，并不是爆破振速随着爆心距的增大而衰减，而是存在着先增大再减小最后在建筑物顶层又有一个放大效应。因此，爆破过程中需要注意对地基的加固处理，以及对建筑物女儿墙、外墙等的防护处理。

4）下穿建筑物后测得的爆破振速明显比下穿前测得的爆破振速大，而在工程施工中，人们往往误认为已经下穿隧道，建筑物就处于安全状态。其实不然，下穿建筑物后，因形成空洞效应，会对爆破振速产生放大效应，本工程下的放大倍数约为1.32～1.69倍。因此，在实际施工中，应重视下穿建筑物后对建筑物的爆破振动监测。

5）轻轨浅埋隧道钻爆循环掘进过程中，沿高程有一个放大效应，已开挖隧道也会产生一个放大效应，建筑物的不同楼层并没有形成一个规律性的衰减规律，因此，在进行爆破设计时，一定要考虑这些放大因素。

[1]沈秀峰.地铁爆破施工对地表建筑物的微振动影响分析[D]. 大连：大连交通大学，2012. Shen Xiufeng. Micro Vibration Influence Analysis of Surface Buildings Caused by the Subway Blasting[D]. Dalian：Dalian Jiaotong University，2012.

[2]高尔新，杨树仁. 爆破工程[M]. 徐州：中国矿业大学出版社，1999：242-256. Gao Erxin，Yang Shuren. The Blasting Engineering[M]. Xuzhou：China University of Mining and Technology Press，1999： 242-256.

[3]言志信，王后峪. 爆破地震效应及安全[M]. 北京：科学出版社，2001：1-2. Yan Zhixin，Wang Houyu. Blasting Seismic Effect and Safety[M]. Beijing：Science Press，2001：1-2.

[4]吕涛，石永强，黄诚，等. 非线性回归法求解爆破振动速度衰减公式参数[J]. 岩土力学，2007，28(9)：1871-1878. L Tao，Shi Yongqiang，Huang Cheng，et al. Study on Attenuation Parameters of Blasting Vibration by Nonlinear Regression Analysis[J]. Rock and Soil Mechanics，2007，28(9)：1871-1878.

[5]张世雄，杨明亮，尹家国，等. 预测爆破波振动强度的经验公式及其在采矿中的应用[J]. 爆破，2000，17(3)：13-17. Zhang Shixiong，Yang Mingliang，Yin Jiaguo，et al. An Empirical Formula of Calculating the Vibrating Intensity of Explosive Wave and Its Application in Mining[J]. Blasting，2000，17(3)：13-17.

[6]张继春，彭琼芳. 岩体爆破地震波衰减规律的现场试验与分析[J]. 辽宁工程技术大学学报：自然科学版，2001，20(4)：399-401. Zhang Jichun，Peng Qiongfang. Field Experiment and Its Analyses of Attenuation Law for Seismic Waves Resulting from Rock Blasting[J]. Journal of Liaoning Technical University：Natural Science Edition，2001，20(4)：399-401.

[7]张天军，马锐，乔宝明，等. 爆破震动中萨道夫斯基拓展式的回归分析[J]. 湖南科技大学学报：自然科学版，2012，27(1)：11-16. Zhang Tianjun，Ma Rui，Qiao Baoming，et al. The Regression Analysis of Extended Sodev Type in Blasting Vibration[J]. Journal of Hunan University of Science & Technology：Natural Science Edition，2012，27(1)：11-16.

[8]朱振海，杨永琪. 沟槽对建筑物减震作用的动光弹研究[J].爆破与冲击，1989，9(1)：55-60. Zhu Zhenhai，Yang Yongqi. Dynamic Photoelastic Studies of the Vibration Damping by a Slop Near a Structure[J]. Explosion and Shock Waves，1989，9(1)：55-60.

[9]魏晓林. 爆破震动对邻近建筑物的危害影响[J].爆破，1998，15(1)：48-54. Wei Xiaolin. Study on Destructive Effect of Blasting Near Building[J]. Blasting，1998，15(1)：48-54.

[10]王俊平，陈宝心. 爆破地震波作用下建筑物的动力响应分析方法[J]. 西部探矿工程，2005，134(9)：134-137. Wang Junping，Chen Baoxin. Analysis Method of Dynamic Response of Building Under Blasting Seismic Wave[J]. West-China Exploration Engineering，2005，134(9)：134-137.

[11]张建波，杨新安，何知思. 浅埋隧道下穿建筑物爆破振动规律及控制研究[J]. 华东交通大学学报，2014，31(1)：17-22. Zhang Jianbo，Yang Xin’an，He Zhisi. Blasting Vibration Rule and Control of Shallow Tunnel Undercrossing Buildings [J]. Journal of East China Jiaotong University，2014，31 (1)：17-22.

[12]郭建群，张继春，曹孝君，等. 穿越高楼下的浅埋隧道掘进控制爆破技术[J].爆破，2003，20(1)：28-30，38. Guo Jianqun，Zhang Jichun，Cao Xiaojun，et al. Controlled Blasting Technique for Excavation of the Shallow Tunnel Under High Buildings[J]. Blasting，2003，20(1)：28-30，38.

[13]唐海，李海波.反映高程放大效应的爆破振动公式研究[J]. 岩土力学，2011，32(3)：820-824. Tang Hai，Li Haibo. Study of Blasting Vibration Formula of Reflecting Amplification Effect on Elevation[J]. Rock and Soil Mechanics，2011，32(3)：820-824.

（责任编辑：廖友媛）

Experimental Study on Blasting Vibration of Light Rail Tunnel Undercrossing Buildings

Wang Hui1，Yang Shengquan1，Chang Zhongmin2，Ding Xiong1，Zhao Leijun1
（1. College of Civil Engineering，Hunan University of Science and Technology，Xiangtan Hunan 411201，China；2. The Third Engineering Co., Ltd. China Railway 16th Bureau Group, HuzhouZhejiang 313000，China)

Taking the shallow light rail tunnel project of Sports Park Station in Chongqing rail transit circle as the research background, made blasting vibration effect experiments of construction channel blasting and drilling excavation undercrossing“ Two Rivers Spring City”. In the early drilling and blasting, calculated the blasting vibration attenuation parameters by monitoring parameters，and through measuring the blasting caused vibration velocity waveforms of different building floors at the light rail tunnel undercrossing buildings, studied the building vibration characteristics as well as the blasting seismic wave propagation and attenuation laws. The research found that the blasting vibration attenuation parameters were =1.88 and k=99.43, and in the process of shallow buried light rail tunnel drilling and blasting excavation，the blasting vibration velocity of the vertical direction is significantly greater than that of horizontal direction，so the study of blasting vibration propagation and attenuation laws as well as the influences of vibration on buildings are premised on the blasting vibration velocity in vertical direction; The blasting vibration velocity increased with the increment of floors at the bottom, decreased with the increment in the middle and increased again with the increment at the top, it did not decrease with the increase of the building floors, which did not meet traditional Steve sadove’s attenuation law. Meanwhile compared the measured blasting vibration velocity before and after light rail tunnel undercrossing buildings, the later exists blasting vibration amplification effect and the magnification is about 1.32～1.69 times.

blasting vibration; vibration characteristics; attenuation law; amplification effect；blasting vibration velocity

U455.3+2

A

1673-9833(2014)06-0017-06

10.3969/j.issn.1673-9833.2014.06.004

2014-10-10

湖南省高校产业化培育基金资助项目 （13CY013），地方级基金资助项目（201443030400184）

王辉（1989-），男，湖南常德人，湖南科技大学硕士生，主要研究方向为岩土工程，E-mail：736352029@qq.com

阳生权（1968-），男，湖南耒阳人，湖南科技大学教授，博士，硕士生导师，主要从事岩土力学与支护方面的教学与研究，E-mail：984336908qq.com