考虑过程阻尼的切削稳定性建模与仿真分析
李忠群,董亚峰,夏磊,彭岳荣,朱帆
(湖南工业大学机械工程学院,湖南株洲412007)
考虑过程阻尼的切削稳定性建模与仿真分析
李忠群,董亚峰,夏磊,彭岳荣,朱帆
(湖南工业大学机械工程学院,湖南株洲412007)
介绍了考虑过程阻尼影响的切削动力学模型,及切削稳定性解析求解方法;利用开发的仿真程序分别对车削和铣削的稳定性进行了仿真分析,模型与仿真程序的正确性得到了切削试验的验证。对比考虑过程阻尼影响前后的切削稳定性叶瓣图发现,考虑过程阻尼影响可显著提高低速区的稳定性极限值。考虑过程阻尼影响的切削稳定性仿真结果,可用于指导航空难加工材料的高效切削。
过程阻尼;切削稳定性;稳定性叶瓣图;高效切削
0 引言
众所周知,颤振是指发生在切削加工中一种自激振动现象,是影响切削加工效率的关键因素。它不仅会降低被加工零件的表面质量和加工精度,而且还会破坏刀具与机床,增加生产成本[1]。稳定性叶瓣图是一种通过动力学建模分析,得到用于预测切削是否稳定的图形,利用该图形可实现高效无颤振切削[2-5]。低速时,由于稳定性叶瓣的致密,导致利用稳定域图形选取切削参数的增效作用消失,其根本原因是,现有模型未考虑过程阻尼的作用。实验研究发现,当切削速度远低于加工系统的固有频率时,系统的稳定切削区域会显著增加(见图1)。这种低速切削时稳定切削区的显著增加,可归结为刀具后刀面与不平工件表面间摩擦作用所导致的切削速度变化,即过程阻尼作用[6-8]。低速时,稳定切削区的增加,对提高航空难加工材料的加工效率尤其重要。由于高速切削此类材料零件时,刀具存在严重磨损现象,因此只能采用中低速切削。目前,过程阻尼已成为切削加工动力学方向的研究热点,相关研究主要有:过程阻尼产生机理[9-11]、过程阻尼建模[12-14]及考虑过程阻尼的稳定性分析[15-17]等。

图1 考虑过程阻尼影响的颤振稳定域示意图Fig.1Schematic diagram for flutter stability domain considering process damping
本文将以考虑过程阻尼的单自由度车削和二自由度铣削稳定性建模分析为基础,实现其颤振稳定性预测,并将模型仿真结果与切削实验结果进行对比,以验证本文所提仿真方法的正确性。
1 考虑过程阻尼的稳定性建模分析
1.1 车削稳定性建模分析
单自由度车削系统动力学方程可描述为
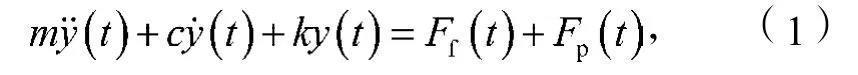
式中:m, c, k分别为系统的质量、粘性阻尼和刚度;
y(t)为y方向的振动量;
Ff为进给力;
Fp为过程阻尼力,它可表示为切削速度v及切削厚度b的函数,即

其中C为过程阻尼系数。
将式(2)代入式(1)可得考虑过程阻尼的动力学方程为
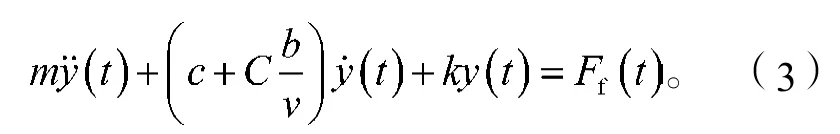
系统在y方向所对应的频响函数为
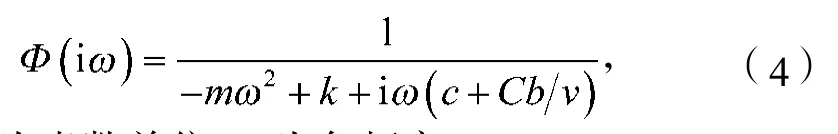
式中:i为虚数单位;为角频率。
对于考虑再生效应的单自由度车削系统而言,其临界稳定性切削厚度可表示为[2]
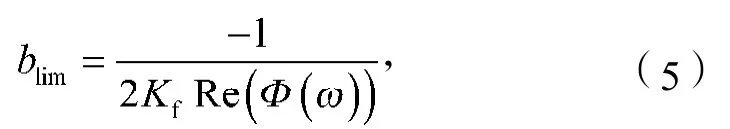
式中:Kf为材料进给方向切削力系数;
Re为实部函数。
假定颤振频率为fc,则留在工件表面的振动波纹数为
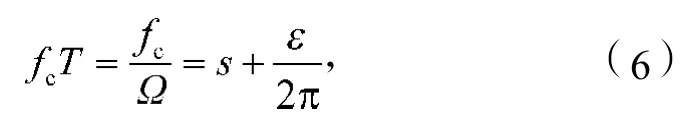
式中:T为切削周期;
s为切削一周产生的整数波纹数;
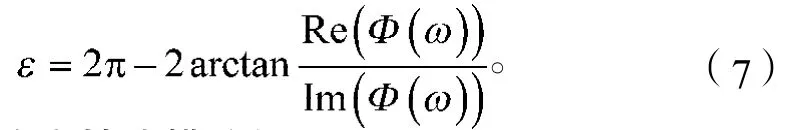
1.2 铣削稳定性建模分析
二自由度铣削系统的动力学方程可表示为

式中:q为系统在力F作用下的响应;
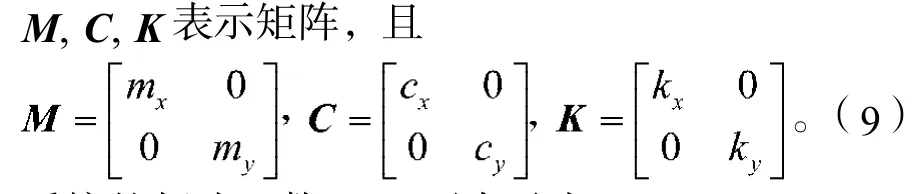
系统的频响函数G()可表示为
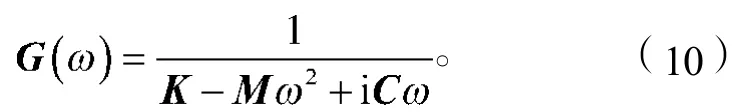
在稳定性边界处,假设颤振频率c处的谐波响应为
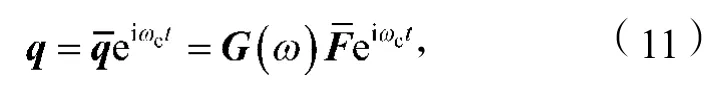
由式(11)可得其延迟项Δq为

铣削过程的动态切削力可表示为
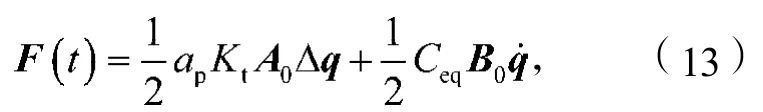
式中:ap为轴向切深;
Kt为切向力系数;
Ceq为等效阻尼;
A0, B0分别为零次谐波下与径向力系数和摩擦因素相关的方向系数[18]。
铣削力F表示成指数形式为

联立求解式(11)~(14)可得
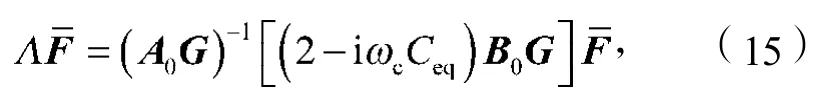
式中,特征值Λ的表达式为

将Λ表示成复数形式Λ=ΛR+iΛI后,将Λ及代入式(16),可得颤振频率处的临界轴向切深为

由于轴向切深ap为实数,故令式(17)中的虚部为零,可得关系式
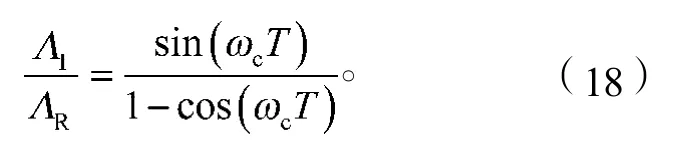
将式(18)代入式(17)的实部可得轴向切深为

假设铣削时留在工件表面的完整波纹数为s,那么有
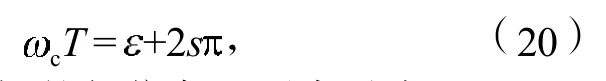
式中为内外调制之间的相位角,可表示为
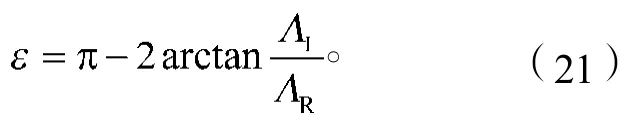
由式(20)可得主轴转速
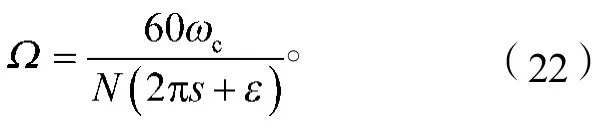
2 切削稳定性仿真与试验验证
2.1 车削稳定性仿真与试验验证
基于上述原理,采用Matlab开发考虑过程阻尼影响的车削稳定性仿真程序,其流程如图2所示。为了研究过程阻尼对切削稳定性的影响,采用实例仿真来分析考虑过程阻尼影响前后,对车削稳定性的影响。
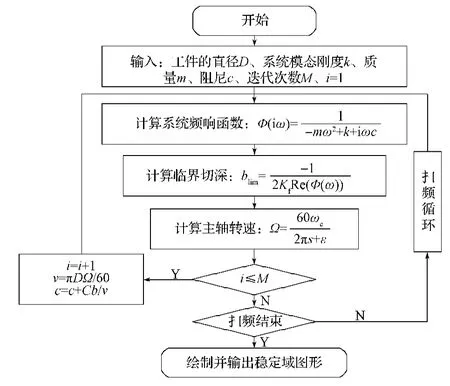
图2 考虑过程阻尼影响的车削稳定性仿真流程图Fig.2Flowchart for turning operation stability simulation considering process damping
仿真实例中所用参数如下:刀具为氮化钛切断刀,悬伸长度为90mm;工件采用直径D=35mm的1018钢;通过锤击实验,采用CutPro对机床-工件系统频响函数曲线进行拟合,得到系统的模态质量m=0.567kg,阻尼c=160N·s/m,刚度k=9.48×106N/m;材料进给方向切削力系数Kf=2.927×109N/m2;过程阻尼系数C=6.11×105N/m[18]。
根据仿真所得的车削稳定性叶瓣图进行试切,过程阻尼对车削稳定性仿真结果的影响如图3所示。通过对比发现:当转速低于4000r/min时,考虑过程阻尼影响模型,可得到更准确的稳定性叶瓣图;当转速较高时,两者均具有较好的预测精度。

图3 过程阻尼对车削颤振稳定性影响与验证Fig.3Effect of process damping on chatter stability of turning process and experimental verification
2.2 铣削稳定性仿真与试验验证
基于上述原理,采用Matlab开发考虑过程阻尼的铣削稳定性仿真程序,其流程图如图4所示。为研究过程阻尼对铣削稳定性的影响,采用实例仿真及切削试验来分析过程阻尼对铣削稳定性仿真结果的影响。
铣削颤振稳定域验证试验在五坐标加工中心FIDIA K197上进行,试验所用铣刀齿数N=3,直径D=18mm,刀尖磨损区宽度W=0.04mm,切入角st=0°,切出角ex=90°。通过锤击实验,采用CutPro软件对机床-刀具系统频响函数进行处理,可得系统主模态的模态刚度k=9×106N/m,阻尼比=0.03,固有频率fn=900Hz;进给方向的切削力系数Kf=2×109N/m,过程阻尼系数C=2×104N/m[18]。在主轴转速范围1000~3800r/min内,以500r/min为增量,从最低轴向切深0.5mm以0.5mm增量开始试切,直到发生颤振。采用Shure麦克风拾取切削噪声并通过FFT(fast fourier transformation)变换,判断是否存在颤振。
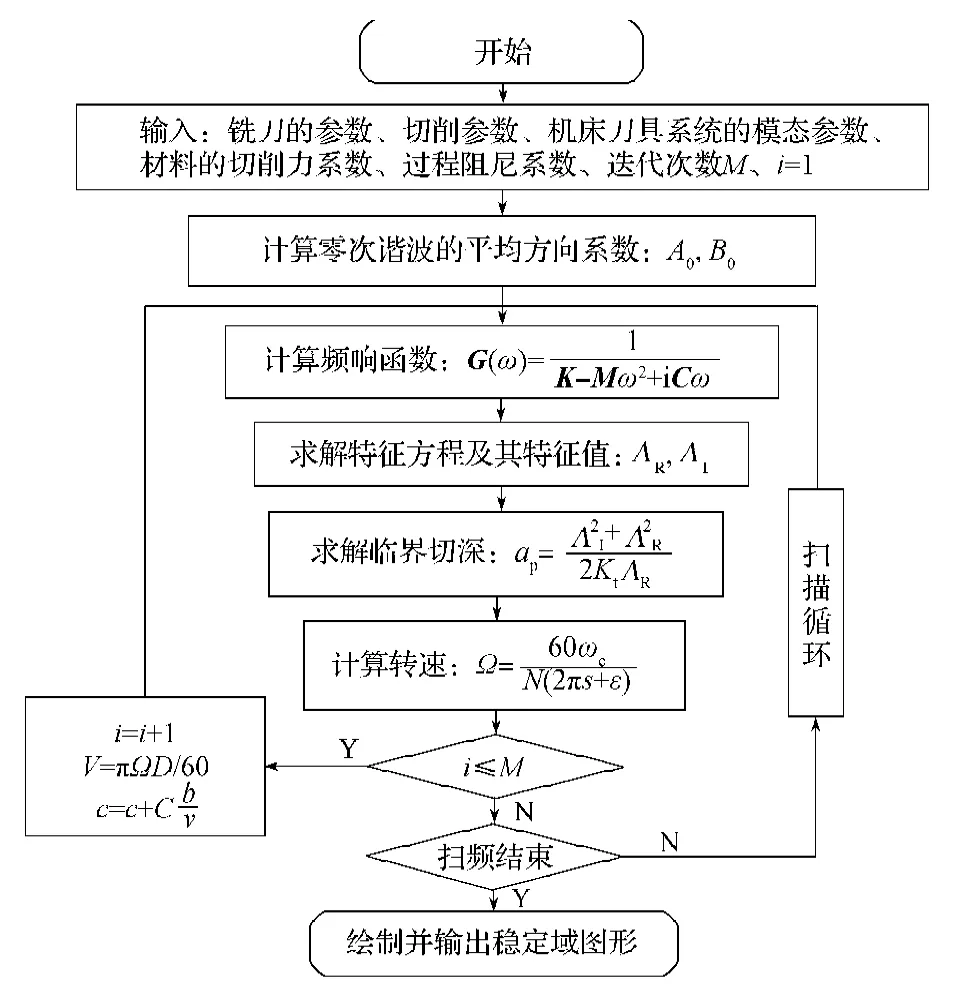
图4 考虑过程阻尼的铣削稳定性仿真流程图Fig.4Flowchart for milling process stability simulation considering process damping
过程阻尼对铣削颤振稳定性仿真结果的影响如图5所示。对比分析发现:与未考虑过程阻尼影响相比,考虑过程阻尼影响后低速区(转速低于2000r/min)的稳定切削区域增加显著,且与切削试验结果吻合;而在高速切削区,无论是否考虑过程阻尼影响,仿真结果均与切削试验结果较吻合。
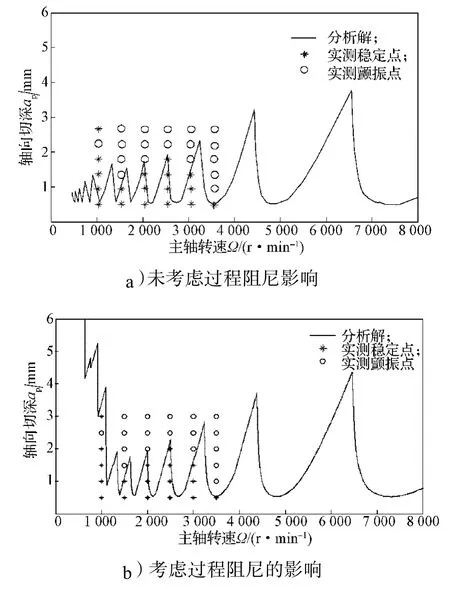
图5 过程阻尼的铣削稳定性影响及试验验证Fig.5Effect of process damping on milling process stability and experimental verification
3 结语
本文分别针对考虑过程阻尼影响的车削及铣削稳定性建模及解析求解等进行了研究,并利用Matlab开发了相应的仿真程序,通过仿真和切削试验验证了模型与仿真算法的正确性。通过对比分析发现,无论是车削还是铣削,过程阻尼的存在导致低速区切削稳定性显著增加。这一发现可用于指导诸如钛合金、镍基合金及淬火钢等航空难加工材料的高效切削加工。
[1]Altintas Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations and CNC Design[M]. 2nd ed. New York:Cambridge University Press,2012:119-139.
[2]Tlusty J,Polacek M. The Stability of Machine Tools Against Self-Excited Vibrations in Machining[C]//ASME International Research in Production Engineering, Pittsburgh. [S. l.]:Production Engineering Conference, 1963:465-474.
[3]Tobias S A. Machine Tool Vibrations[M]. Glasgow:Blackie and Sons Ltd.,1965:62-73.
[4]Tlusty J,Zaton W,Ismail F. Stability Lobes in Milling[J]. Annals of the CIRP,1983,32(1):309-313.
[5]Altintas Y,Budak E. Analytical Prediction of Stability Lobes in Milling[J]. CIRP Annals-Manufacturing Technology,1995,44(1):357-362.
[6]Dsa M K,Tobias S A. The Relation between the Static and the Dynamic Cutting of Metals[J]. International Journal of Machine Tool Design,1967(7):63-89.
[7]Altintas Y,Weck M. Chatter Stability in Metal Cutting and Grinding[J]. CIRP Annals-Manufacturing Technology,2004,53(2):619-642.
[8]Sisson T R,Kegg R L. An Explanation of Low-Speed Chatter Effects[J]. Journal of Engineering for Industry, 1969,91(5):951-958.
[9]Wallace P W,Andrew C. Machining Forces: Some Effects of Tool Vibration[J]. Journal of Mechanical Engineering Science,1965,7(3):152-162.
[10]Peters J,Vanherck P,Van Brussel H. The Measurement of the Dynamic Cutting Coefficient[J]. Annals of the CIRP,1971,21(2):129-36.
[11]Tlusty J. Analysis of the State of Research in Cutting Dynamics[J]. Annals of the CIRP,1978,27(2),583-589.
[12]Huang C Y,Wang J J. Mechanistic Modeling of Process Damping in Peripheral Milling[J]. Journal of Manufacturing Science and Engineering,2007,129(2):12-20.
[13]Montgomery D,Altintas Y. Mechanism of Cutting Force and Surface Generation in Dynamic Milling[J]. ASME J. Eng. Ind.,1991,113(2):160-168.
[14]Budak E,Tunc L T. Identification and Modeling of Process Damping in Turning and Milling Using a New Approach[J]. CIRP Annals-Manufacturing Technology,2010,59(1):403-408.
[15]Ahmadi K,Ismail F. Experimental Investigation of Process Damping Nonlinearity in Machining Chatter[J]. International Journal of Machine Tools and Manufacture 2010,50(3):1006-1014.
[16]Tyler C T,Schmitz T L. Analytical Process Damping Stability Prediction[J]. Journal of Manufacturing Processes, 2013,15(1):69-76.
[17]Ahmadi K, Ismail F. Stability Lobes in Milling Including Process Damping and Utilizing Multi-Frequency and Semi-Discretization Methods[J]. International Journal of Machine Tools and Manufacture,2012,54(1):46-54.
[18]Ahmadi K,Ismail F. Analytical Stability Lobes Including Nonlinear Process Damping Effect on Machining Chatter [J]. International Journal of Machine Tools & Manufacture,2011,51(2):296-308.
(责任编辑:邓光辉)
Modeling and Simulation on Cutting Process Stability Considering Damping
Li Zhongqun,Dong Yafeng,Xia Lei,Peng Yuerong,Zhu Fan
(School of Mechanical Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
Introduces a cutting dynamic model considering process damping and its analytical solution to the cutting stability. Applies the developed simulation program to simulate and analyze the stability of turning and milling operations respectively, and the cutting tests verify the correctness of the proposed model and the simulated program. Compares the cutting stability lobe diagram with and without considering process damping, and finds that the stability limit is improved remarkably at low cutting speeds when the effect of process damping is considered. The cutting stability simulation approach considering process damping is applicable for high efficiency cutting of aeronautical hard-to-machine materials.
process damping;cutting process stability;stability lobe diagram;high performance cutting
TH113.1
A
1673-9833(2014)06-0023-04
10.3969/j.issn.1673-9833.2014.06.005
2014-10-12
国家自然科学基金资助项目(51375160, 51375161),国家科技重大专项基金资助项目(2012ZX04011-011)
李忠群(1966-),男,湖南东安人,湖南工业大学教授,博士,主要研究方向为数字化制造与装备技术,虚拟制造,E-mail:zhqunli@163.com

