基于正态分布优先集结算子的随机多准则群决策方法

张腊娥，汪新凡

（1. 湖南工业大学财经学院，湖南株洲412007；2. 湖南有色金属职业技术学院基础课部，湖南株洲412006；3. 湖南工业大学理学院，湖南株洲412007）

基于正态分布优先集结算子的随机多准则群决策方法

张腊娥1,2，汪新凡3

（1. 湖南工业大学财经学院，湖南株洲412007；2. 湖南有色金属职业技术学院基础课部，湖南株洲412006；3. 湖南工业大学理学院，湖南株洲412007）

对准则值为正态随机变量，而准则之间具有优先级别的随机多准则群决策问题进行了研究。首先，定义了一种集结正态分布数的优先加权平均（NDNPWA）算子，并给出了该算子的相关性质；进一步，基于NDNPWA算子和正态分布数加权算术平均（NDNWAA）算子，提出了一种准则值为正态随机变量，准则之间具有优先级别，而决策者之间不具有优先级别的随机多准则群决策方法。最后，通过实例分析表明，该方法具有可行性和有效性。

群决策；正态分布；NDNPWA算子

1 研究背景

多准则决策（multi-criteria decision making，MCDM）是指决策者为了完成某项目标而在考虑多个准则的情况下，从有限个可行方案中挑选最佳方案，或者对方案进行排序的过程。MCDM是当代决策科学的重要组成部分，在工程设计、经济、管理及军事等诸多领域中有广泛应用，从而受到人们的高度关注。在随机不确定环境下，MCDM问题中的准则值往往为随机变量的形式。特别地，由于正态分布是一种非常重要的概率分布，具有普适性，在许多情形下适合于描述准则值的随机变化，因而很多随机MCDM问题中的准则值为正态随机变量的形式。这类准则值为正态随机变量的MCDM问题（称为正态随机MCDM问题）不仅大量存在，而且具有重要的理论意义和实际价值，已引起研究者的高度重视。目前，正态随机MCDM问题的处理方法一般有5种：1）SMAA（stochastic multi-objective acceptability analysis）方法[1]；2）基于粗糙集的方法[2]；3）基于随机占优的方法[3]；4）基于区间数的方法[4]；5）基于集结算子的方法[5]。基于集结算子的方法给出了正态分布数的运算法则，定义了正态分布数加权算术平均（normal distribution number weighted arithmetic averaging，NDNWAA）算子，并给出了一种准则权重信息不完全确定，而准则值为正态随机变量的动态随机多准则决策方法。上述正态随机MCDM方法各有特点，但它们仅考虑了各准则处于同一优先级别的情形。

在实际的决策过程中，有时需要考虑各准则之间优先级别不同的情形。例如，高校在引进博士时，首先需要考察应聘者的思想品德，即思想品德这个准则享有最高级别的优先权。如果某应聘者思想品德不好，那么即使其科研和教学特别突出也不能引进。R. R. Yager[6-7]最早对该类问题进行探究，并用文献检索问题、购买自行车问题和组织管理问题等来说明这类情形，并提出了集结相应决策信息的优先平均（prioritized averaging，PA）算子[6]和优先有序加权平均（prioritized ordered weighted averaging，POWA）算子[7]。

由上述分析可知，准则之间具有优先级别的正态随机MCDM问题缺乏研究，而现有的正态随机MCDM方法均无法解决这类问题。因此，本文将聚焦于这类问题，拟在NDNWAA算子和PA算子的基础上，提出一种正态分布数优先加权平均（normal distribution number prioritized weighted averaging， NDNPWA）算子，研究其性质，进而基于该算子提出一种准则值为正态随机变量，且准则之间具有优先级别的多准则群决策（multi-criteria group decision making，MCGDM）方法，并进行实例分析。

2 预备知识

2.1 正态分布数及其相关概念

正态分布是一种由下面的概率密度函数，即高斯函数所确定的连续的概率分布[4]：

3 正态分布数优先集结算子

根据定义2、定义3和定义5，本章给出一种准则具有优先级别情形下，集结正态分布数的优先加权平均（NDNPWA）算子。

证明显然，由式（5）集结得到的结果仍为正态分布数。下面用数学归纳法证明式（6）。

1）当n=2时，由于

2）假设当n=k时式（6）成立，即

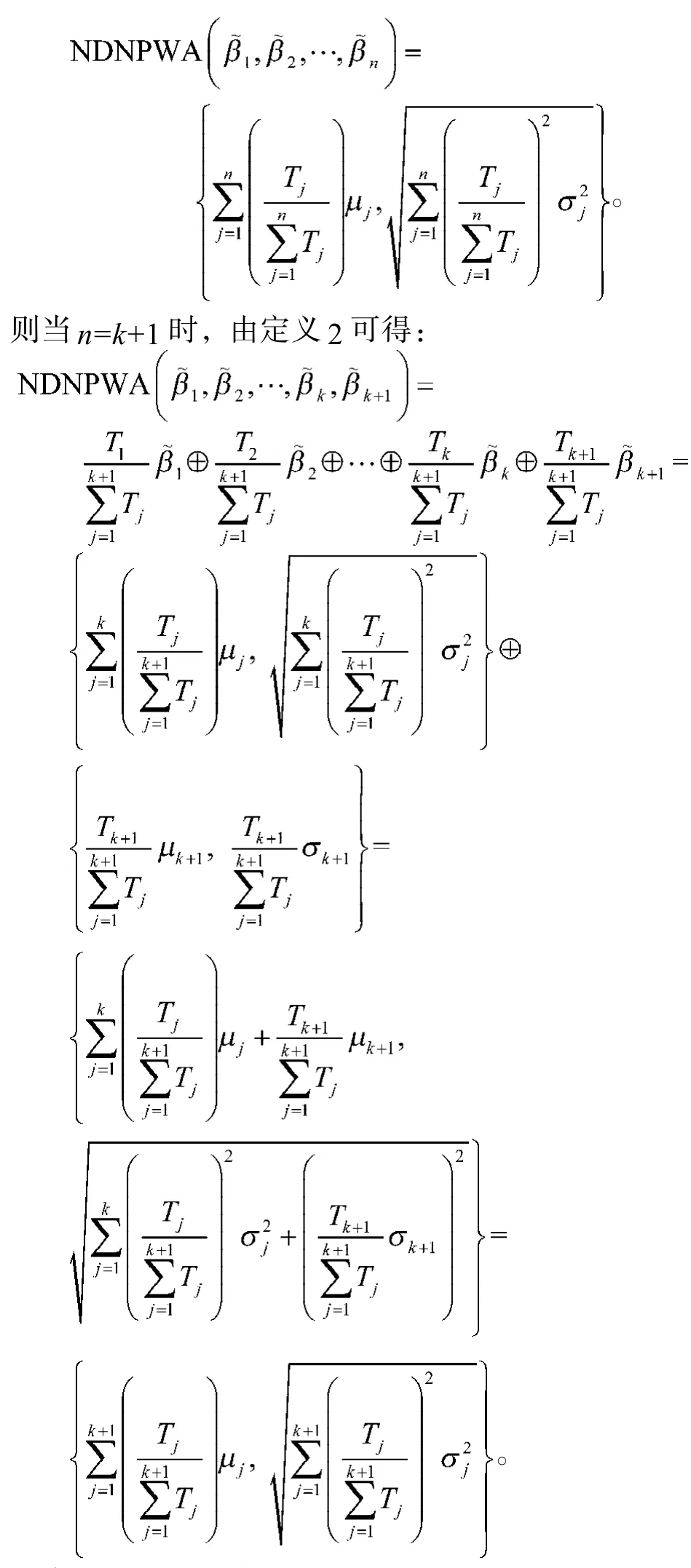
即当n=k+1时，式（6）也成立。

综合1）和2）可得，对n∈N且n≥2时，式（6）均成立。定理2 证毕。

NDNPWA算子具有以下些性质：

4 基于NDNPWA算子的MCGDM方法

根据上述决策信息，以下给出一种基于NDNPWA算子的MCGDM方法，具体步骤如下：

步骤1利用NDNWAA算子

方案Ai(i=1, 2, …, m)进行排序，并选择最优方案。

5 实例分析

某风险投资公司决定选择一些项目进行投资。现有5个投资方案Ai(i=1, 2, …, 5)可供选择，考核指标（即准则）有：投资额C1（万元），风险损失值C2（万元），风险盈利值C3（万元）[5]，它们之间存在优先级别。现由3位决策专家（决策专家e1为董事长，决策专家e2为投资公司经理，决策专家e3为专家，他们的权重向量为）对上述3项指标进行评估。评估的初始随机决策矩阵（k=1, 2, 3）见表1～3，试确定最优方案。

表1 初始随机决策矩阵D(1)Table1Initial random decision matrix D(1)

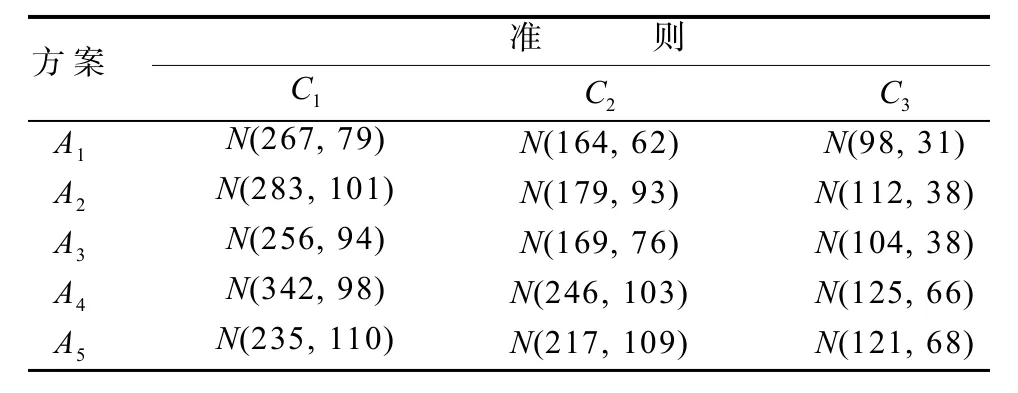
表2 初始随机决策矩阵D(2)Table2Initial nitial random decision matrix D(2)

表3 初始随机决策矩阵D(3)Table3Initial random decision matrix D(3)

下面利用本文提出的决策方法求解。

步骤1利用NDNWAA算子，即式（11），把3个决策专家ek（k=1, 2, 3）给出的初始随机决策矩阵（k=1, 2, 3）集结为群体评价值矩阵，见表4。

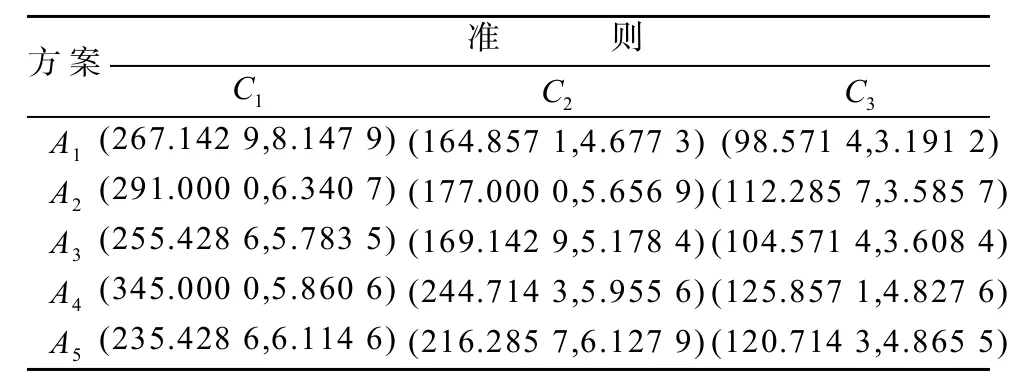
表4 群体评价值矩阵BTable4Group evaluation value matrix B

表5 规范化的群体评价值矩阵Table5Normalized group evaluation value matrix

表5 规范化的群体评价值矩阵Table5Normalized group evaluation value matrix

方案准则C2C3A1 A2 A3 A4 A5 C1 (0.8813, 0.0236) (0.8090, 0.0184) (0.9217, 0.0168) (0.6824, 0.0170) (1.0000, 0.0177) (1.0000, 0.0191) (0.9314, 0.0231) (0.9747, 0.0212) (0.6737, 0.0243) (0.7622, 0.0250) (0.7832, 0.0254) (0.8922, 0.0285) (0.8309, 0.0287) (1.0000, 0.0384) (0.9591, 0.0387)

步骤3利用式（15）计算得到准则优先权重Tij(i=1, 2, …, 5；j=1, 2, 3)：

6 结语

本文针对准则值为正态随机变量，而准则之间具有优先级别的随机MCGDM问题，在NDNWAA算子和PA算子的基础上，定义了一种考虑准则之间具有优先级别的正态分布数集结算子，即NDNPWA算子，并研究了该算子的相关性质。进一步，基于NDNPWA算子和NDNWAA算子，提出了一种准则值为正态随机变量，准则之间具有优先级别，而决策者之间不具有优先级别的随机MCGDM方法，且详细给出了该方法的步骤。最后，通过一个实际例子对本文提出方法的可行性和有效性进行了验证。实例验证表明，本文提出的决策方法是可行的、有效的。由于现实中准则值为正态随机变量的MCDM问题大量存在，准则之间具有优先级别的情形也大量存在，因而本文的研究具有重要的实际意义和应用价值，可广泛应用于供应链管理、应急管理、项目评估、维修服务以及军事系统效能评价等相关决策中。

[1]Lahdelma R，Makkonen S，Salminen P. Multivariate Gaussian Criteria in SMAA[J]. European Journal of Operational Research，2006，170 (3)：957-970.

[2]Yao S B，Yue C Y. Approach to Stochastic Multi-Attribute Decision Problems Using Rough Sets Theory[J]. Journal of Systems Engineering and Electronics，2006， 17 (1)：103-108.

[3]姜广田，樊治平，刘洋，等. 一种具有正态随机变量的多属性决策方法[J]. 控制与决策，2009，24(8)：1187-1191. Jiang Guangtian，Fan Zhiping，Liu Yang，et al. Method for Multiple Attribute Decision Making with Normal Random Variables[J]. Control and Decision，2009，24(8)：1187-1191.

[4]王坚强，任剑.基于WC-OWA算子的随机多准则决策方法[J]. 控制与决策，2007，22 (12)：1429-1432. Wang Jianqiang，Ren Jian. Stochastic Multi-Criteria Decision-Making Method Based on WC-OWA Operator [J]. Control and Decision，2007，22(12)： 1429-1432.

[5]汪新凡，杨小娟. 信息不完全确定的动态随机多属性决策方法[J]. 系统工程理论与实践，2010，30 (2)：332-338. Wang Xinfan，Yang Xiaojuan. Dynamic Stochastic Multiple Attribute Decision Making Method with Incomplete Certain Information[J]. Systems Engineering-Theory & Practice，2010，30(2)：332-338.

[6]Yager R R. Prioritized Aggregation Operators[J]. International Journal of Approximate Reasoning，2008，48 (1)：263-274.

[7]Yager R R. Prioritized OWA aggregation[J]. Fuzzy Optimization and Decision Making，2009，8(3)：245-262.

（责任编辑：邓光辉）

Approach to Stochastic Multi-Criteria Group Decision Making Based on Normal Distribution Prioritized Aggregation Operator

Zhang Lae1,2，Wang Xinfan3
（1. School of Finance & Economics，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. Department of Fundamental Courses，Hunan Nonferrous Metals Vocational and Technical College，Zhuzhou Hunan 412006，China；3. School of Science，Hunan University of Technology，Zhuzhou Hunan 412007，China）

Investigates stochastic multi-criteria group decision making problems in which the criterion values are normal random variables and the criteria are in different priority levels. First, defines a new aggregation operator named normal distribution number prioritized weighted averaging (NDNPWA) operator and provides the relative properties of the operator. Furthermore, based on the NDNPWA operator and the normal distribution number weighted arithmetic averaging (NDNWAA) operator, proposes an approach for solving the stochastic multi-criteria group decision making problems in which the criterion values are normal random variables, the criteria are in different priority levels and the decision makers are not in different priority levels. Finally, presents an illustrative example to demonstrate the feasibility and effectiveness of the developed method.

group decision making；normal distribution；NDNPWA operator

C934

A

1673-9833(2014)06-0001-06

10.3969/j.issn.1673-9833.2014.06.001

2014-09-27

国家自然科学基金资助项目（71271218， 71221061），教育部人文社科基金资助项目（12YJA630114, 13YJC630200），湖南省自然科学基金资助项目（2015JJ2047）

张腊娥（1981-），女，湖南冷水江人，湖南有色金属职业技术学院讲师，湖南工业大学硕士生，主要研究方向为投资项目决策与风险管理，E-mail：179486581@qq.com

汪新凡（1966-），男，湖南安化人，湖南工业大学教授，博士，主要从事不确定决策和集结算子等研究，E-mail：zzwxfydm@126.com