基于Matlab的正交面齿轮设计及可视化分析

赵磊，明兴祖，王伟，李曼德

（湖南工业大学机械工程学院，湖南株洲412007）

基于Matlab的正交面齿轮设计及可视化分析

赵磊，明兴祖，王伟，李曼德

（湖南工业大学机械工程学院，湖南株洲412007）

基于正交面齿轮齿面方程，利用Matlab软件，对最大外径系数、最小内径系数和最大齿宽系数与刀具齿数和传动比之间的关系分别进行分析。依据齿面方程分析的结论对齿宽和齿高离散，计算出齿面各点坐标，并依此绘制出全齿图形；通过与面齿轮实物齿面的对比，证明了此离散方法所得的模型具有较高的准确性。

面齿轮建模；最大外径系数；最小内径系数；最大齿宽系数

0 引言

面齿轮传动是一种新型齿轮传动模式，国外研究者对此研究较早并应用于军事等领域[1]，但我国研究起步比较晚。面齿轮传动的优点较多，比如小齿轮为渐开线圆柱直齿轮，其轴向移动产生的误差对传动性能几乎没有影响；面齿轮传动比普通锥齿轮传动具有较大的重合度；渐开线圆柱直齿轮上无轴向力作用；面齿轮用于传动装置时传动振动小和噪音低等特点[2-3]。

在对面齿轮的研究中，无论进行机床误差分析、磨削热应力分析还是传动应力分析等，都是以齿轮的基本参数如面齿轮的最大外半径、面齿轮的最小内半径的数据和齿面齿廓的生成模型为基础的研究。在F. L. Litvin等的研究中[4]，对面齿轮最大外径系数、最小内径系数等基本参数和刀具齿数的关系进行了分析，虽然添加了个别特定传动比关系，但是在二维图像中无法详尽地观察变化规律。在朱如鹏对面齿轮建模的研究中[5]，由Matlab得到单齿面图形，再导入三维绘图软件进行建模。如果因为Matlab数据误差较大，再进行修改，效率会明显下降。本文在数据分析方面添加了传动比与半径系数的关系，所绘制出的三维图像可以更直观地得到面齿轮最大外径系数、最小内径系数等基本参数与传动比和刀具齿数的变化关系。在Matlab中建立全齿图像，可提高三维模型建立的效率，并在进行三维建模前得到较为准确的数据。

1 齿面方程建立

1.1 工作曲面方程的建立

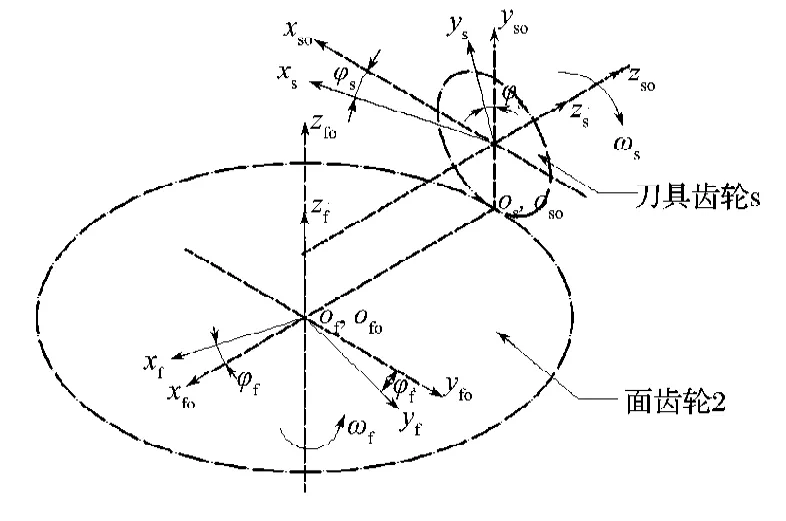
图1 加工面齿轮坐标系Fig.1The coordinate system for face-gear processing

1.2 正交面齿轮齿根过渡曲面基本方程

面齿轮的齿根过渡曲面是加工时插齿刀齿顶所形成的轨迹面[6]，用代替插齿刀齿面参数有

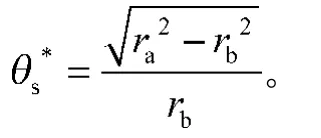
式中ra为插齿刀齿顶圆半径。

再经坐标系转换可得过度曲面方程，即

在不发生根切的情况下，面齿轮的工作齿面与齿根过渡曲面会有一条公切线，这条公切线也满足啮合方程，因此当时，代入啮合方程可得到过渡曲线方程：

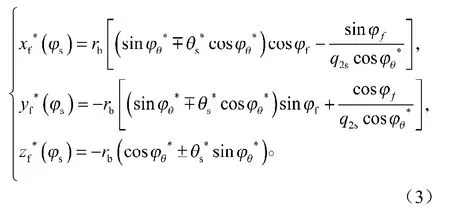
2 正交面齿轮的设计

2.1 面齿轮不发生根切的最小半径的确定

根切临界点为插齿刀齿顶圆与根切界限处的交点[7]。插齿刀齿顶圆处的参数s可以确定为

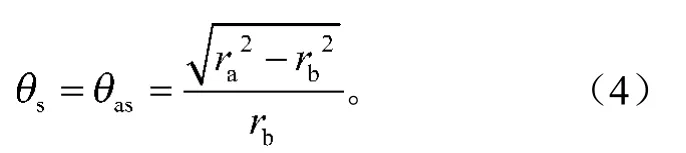
将式（4）得到的s代入方程，可以解出对应s的值，将此处的s和的值代入面齿轮齿面方程中可以得出对应面齿轮齿面上点坐标的值，因此，面齿轮齿面不产生根切的最小内径为

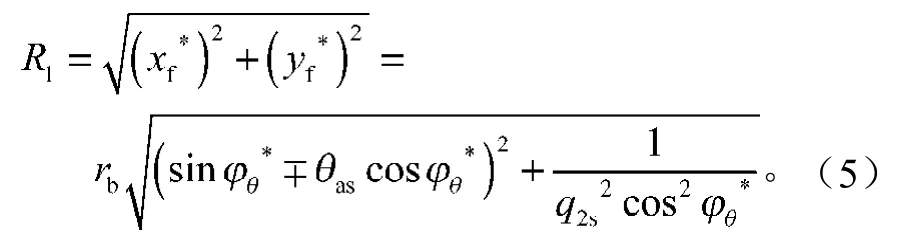
应用Matlab数值分析和三维绘图功能，编制程序并绘制正交面齿轮最小内半径系数Rmin与刀具齿数s和刀具与面齿轮齿数比q2s的关系，如图2所示。

图2 正交面齿轮最小内半径系数R1关系图Fig.2The relationship diagram for orthogonal face-gear minimum inner radius coefficient R1

由图2可知，面齿轮最小内半径系数Rmin与插齿刀齿数近似于线性增加的关系；在相同参数条件情况下，Rmin随插齿刀压力角增大而减小，减小的幅度随刀具与面齿轮齿数比及传动比q2s的增大而减小。由面齿轮最小内半径系数的变化进而可推知面齿轮最小内半径与各参数之间的关系，因为将图中的纵坐标Rmin的值乘上模数就是面齿轮最小内半径R1的值。

2.2 正交面齿轮齿顶不变尖的最大外半径的确定

当面齿轮发生齿顶变尖的时候[8]，齿厚方向为零及xf=0，由面齿轮的生成原理可知f=-rb，将数值带入面齿轮齿面方程可求得相应的及

定义无量纲参数Rmax=R2/M为最大外半径系数，Rmax为

由计算机编程绘制的正交面齿轮最大外半径系数Rmax与刀具齿数和刀具与面齿轮齿数比及传动比q2s的关系如图3所示。

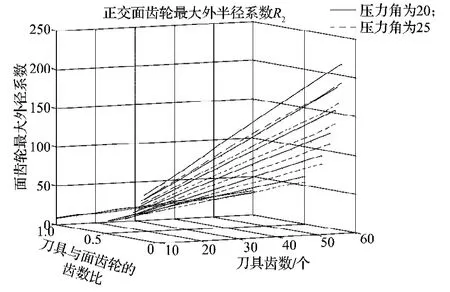
图3 正交面齿轮最大外半径系数R2关系图Fig.3The relationship diagram for orthogonal face-gear maximum outer radius coefficient R2

由图3可以看出，正交面齿轮最大外半径系数Rmax与插齿刀齿数近似于线性增加的关系；在相同参数条件情况下，Rmax随插齿刀压力角增大而减小，减小的幅度随传动比及刀具与面齿轮齿数比q2s的增大而减小。由面齿轮最大外半径系数的变化进而可推知面齿轮最大外半径与各参数之间的关系，因为将图中的纵坐标Rmax的值乘上模数就是面齿轮最大外径R2的值。

2.3 正交面齿轮的最大齿宽系数

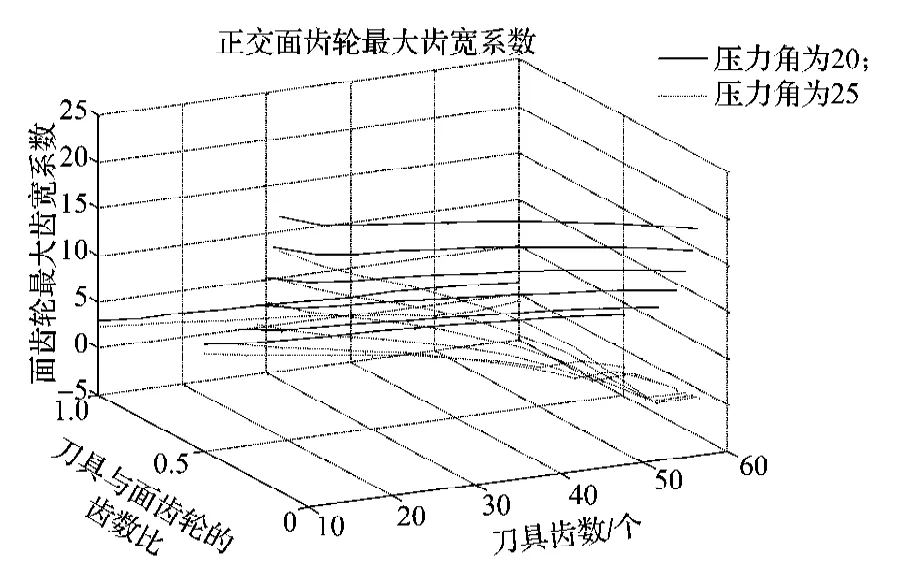
图4 正交面齿轮最大齿宽系数关系图Fig.4The relationship diagram for orthogonal face-gear maximum tooth width coefficient

从图可知Cmax主要与传动比有关，在不同的压力角下都是先减小后增大；刀具齿数相同时，传动比越小，正交面齿轮的最大齿宽系数增大。在实际使用中，实际面齿轮的齿宽应该小于图中面齿轮最大齿宽系数乘于模数。

2.4 正交面齿轮的设计实例

面齿轮的设计中已知参数分别为：渐开线圆柱直齿轮齿数s，模数M，齿顶高系数h*a，齿根高系数c*，分度圆压力角和面齿轮齿数Z2。为了避免边缘接触，所使用插刀齿轮的齿数要比啮合传动齿轮的齿数多1～3个[9]。

根据以上推导的公式，利用Matlab编程计算[10]，可得面齿轮的最大外半径和最小内半径。本文以国内某航空发动机研究所加工出的面齿轮为分析对象，其主要参数如表1所示。

表1 面齿轮主要参数Table1The parameters of face-gear

在实际加工中要求加工的面齿轮内半径要大于面齿轮的最小内半径，才不会出现根切现象，加工外半径要小于最大外半径才不会出现尖顶现象，但由于齿的强度要求，外半径比最大外半径小很多。实际正交面齿轮的加工内外径分别是内半径为143mm，外半径为170mm。由于加工内半径大于最小内半径，加工外半径小于最大外半径，所以方案可行。

3 正交面齿轮的可视化

3.1 正交面齿轮单齿可视化

由于面齿轮齿面的复杂性，要较为精确地建立模型，使用单一的三维绘图软件如Proe, UG是比较困难的。本文以Matlab软件为中介，可以较为准确地计算出齿面上各点坐标，再把相应的坐标数值导入相应的三维作图软件中，就可以对正交面齿轮进行建模。

首先，判断确定参数的范围。由图1和渐开线圆柱直齿轮刀具齿面方程可以确定的取值范围。由图2可以得到知面齿轮的y,轴的范围，面齿轮齿面方程中xf对应于渐开线圆柱直齿轮刀具的齿宽，yf对应于渐开线圆柱直齿轮刀具的齿厚，f对应于渐开线圆柱直齿轮刀具的齿高，由此可以确定其相应的取值范围。因此只要对其中的2个方程的数值进行离散化，就可以计算出全部的齿面坐标。

根据表1的相关数据，通过Matlab的数学建模进行面齿轮的可视化，结果如图5所示。

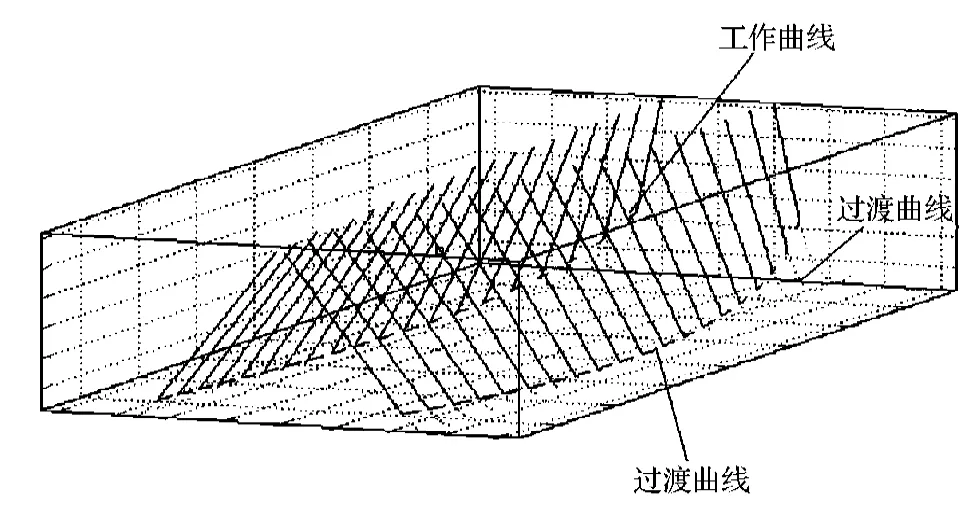
图5 面齿轮单个齿的齿廓Fig.5The face-gear profile of single tooth

3.2 正交面齿轮三维实体模型

通过Matlab计算齿面上各点数据，将数据导入相应的三维作图软件进行建模[11]。本文以Proe为例，经过导入样条曲线、曲面拟合、实体化、阵列等过程，可得相应的面齿轮模型，如图6所示。

图6 面齿轮三维实体Fig.6The 3D face-gear

本文以美国M & M公司的Sigma7齿轮测量中心对正交面齿轮齿面齿廓偏差进行测量，可得到面齿轮实物误差。面齿轮实物齿面偏差如图7所示。

对建立面齿轮齿面误差进行分析可得面齿轮齿面齿廓误差[12]如图8所示。

由齿面坐标、图7和图8，进行分析比较可知：建模仿真的最大误差为-0.0442mm；实测出的最大误差为-0.0285mm。综合分析两者的数据，可知所建模型的误差与实测误差很接近，验证了本建模方法的可行性。

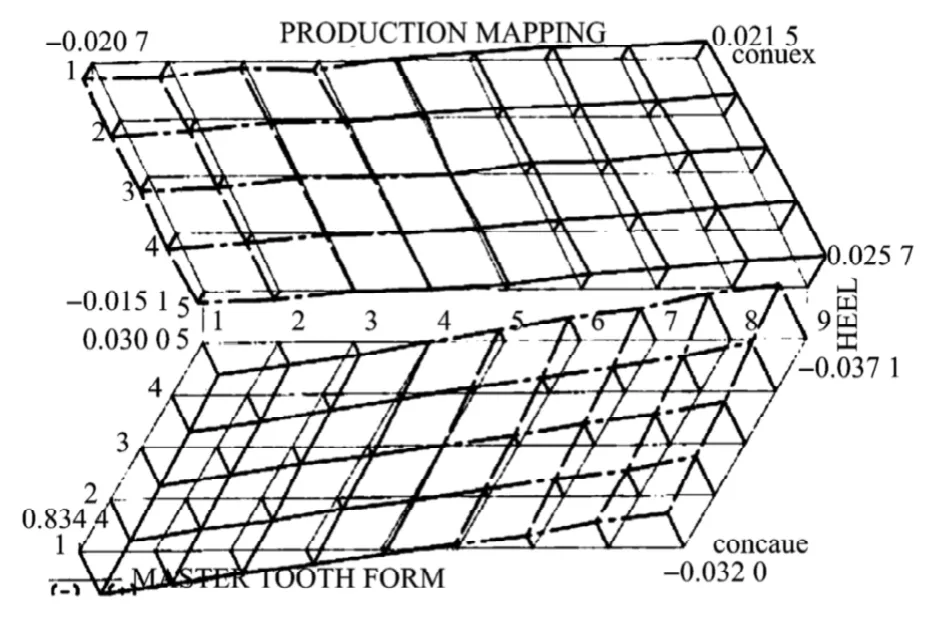
图7 面齿轮实物齿面偏差Fig.7The real tooth surface deviation of face-gear

图8 面齿轮齿面齿廓误差Fig.8The profile error of face-gear tooth surface

4 结语

通过正交面齿轮的根切和尖顶现象，利用Matlab软件计算得到正交面齿轮的最小内半径和最大外半径。本文对无量纲参数Rmax, Rmin, Cmax相关的参数q2s, Zs三者之间的关系进行分析，它们可近似为线性关系，对之后的正交面齿轮设计提供便利。在计算正交面齿轮齿面坐标中，本文采取离散yf,f，在Matlab软件中绘制单齿图形，再把数据导入Proe软件中，可更方便快捷地得知面齿轮齿面坐标的准确程度。在与实物对比中得到的离散yf,f所得到的面齿轮模型具备可应用性，为之后的面齿轮数字化制造研究提供基础。

[1]Handschuh. Experimental Testing of Prototype Face Gears for Helicopter Transmissions[R]. Solihull：NASA Technical Memorandum，1992：129-136.

[2]Barone S，Borgianni L，Forte P. Evaluation of the Effect of Misalignment and Profile Modification in Face Gear Drive by a Finite Element Meshing Simulation[J]. Journal of Mechanical Design，2004，126(5)：916-924.

[3]Litivin F L，Zhang Y，Wang J C，et al. Design and Geometry of Face Gear Drive[J]. Journal of Mechanical Design，1992，114(4)：642-647.

[4]David G L，Robert F H，Gregory F H，et al. Evaluation of Carburized and Ground Face Gears[J]. Journal of the American Helicopter Society，1999，45(2)：118-124.

[5]朱如鹏. 面齿轮传动的啮合特性研究[D]. 南京：南京航空航天大学，2000. Zhu Rupeng. Study of Drive Meshing Characteristics of Face Gear[D]. Nanjing：Nanjing University of Aeronautics and Astronautics，2000.

[6]李政民卿，朱如鹏. 基于包络法的正交面齿轮齿廓尖化研究[J]. 中国机械工程，2008，19(9)：1029-1032. Li Zhengminqing，Zhu Rupeng. Research on Pointing of Face Gear by Enveloping Method[J]. China Mechanical Engineering，2008，19(9)：1029-1032.

[7]勒广虎. 正交面齿轮传动的强度与动力学特性分析研究[D]. 南京：南京航空航天大学，2012. Jin Guanghu. Research on Strength and Dynamic Characteristics of Orthogonal Face Gear Drives[D]. Nanjing：Nanjing University of Aeronautics and Astronautics，2012.

[8]吴亚男. 面齿轮滚齿加工方法的研究[D]. 哈尔滨：哈尔滨工业大学，2013. Wu Ya’nan. Research on Hobbing Method of Face Gear [D]. Harbin：Harbin Institute of Technology，2013.

[9]李大庆. 直齿面齿轮啮合性能预控及蝶形砂轮磨齿关键技术研究[D]. 镇江：江苏大学，2013. Li Daqing. Research on Pre-Control Method of Meshing Behavior and Key Technologies for Grinding Face Gear by Dish Wheel[D]. ZhenJiang：JiangSu University，2013.

[10]Litivin F L，Egelja A，Tan J. Handbook on Face Gear Drives with a Spur Involute Pinion[R]. Washington：NASA Final Contractor Report CR-209909，2000.

[11]张晋西，郭学琴. 齿轮三维参数化建模与加工运动仿真[J]. 机械设计，2002，19(3)：33-35. Zhang Jinxi，Guo Xueqin. Gear 3D Parametric Modeling and Machining Motion Simulation[J]. Mechanical Design ，2002，19(3)：33-35.

[12]明兴祖，胡京明，刘赣华. 螺旋锥齿轮数控磨削表面粗糙度的建模与分析[J]. 湖南工业大学学报，2009，23(2)：37-44. Ming Xingzu，Hu Jingming，Liu Ganhua. Research on Surface Roughness for Multi-Axis NC Grinding of Bevel Gear[J]. Journal of Hunan University of Technology，2009，23(2)：37-44.

（责任编辑：申剑）

Matlab-Based Orthogonal Face-Gear Design and Visualization Analysis

Zhao Lei，Ming Xingzu，Wang Wei，Li Mande
（School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

Based on the orthogonal face-gear tooth surface equation, analyzes the relationship of maximum outer diameter coefficient, minimum inner diameter coefficient and the coefficient of maximum tooth width with the cutter teeth and gear ratio by Matlab software. According to the analysis of tooth surface equation, the tooth width and tooth height are discrete, calculates the coordinates of the points of tooth surface, and then draws the whole tooth pattern; Compared with face-gear real tooth surface, proves that the model established by the discrete method has higher accuracy.

face gear modeling ；maximum outer diameter coefficient ；minimum inner diameter coefficient；coefficient of maximum tooth width

TH132. 41

A

1673-9833(2014)05-0038-05

10.3969/j.issn.1673-9833.2014.05.008

2014-04-13

国家自然科学基金资助项目（51375161, 51375160）

赵磊（1989-），男，河南濮阳人，湖南工业大学硕士生，主要研究方向为数字化制造技术，E-mail：2312189378@qq.com

明兴祖（1964-），男，湖南常德人，湖南工业大学教授，硕士生导师，博士，主要从事数字化制造理论与技术方面的研究，E-mail：mxz9036@126.com