基于受力计算的深基坑支护设计优化方法

龚旭东

(中铁第一勘察设计院集团公司，陕西西安 710043)

由于城市地铁大多修建在高楼林立的地区，为降低地铁隧道始发井、风井等基坑施工对建筑物的影响，对基坑开挖过程中所产生的地层变形与地表沉降提出了严格的要求。目前，对深基坑支护方式、时机以及钢支撑等支护位置的选取并没有十分明确的方法，大多停留在经验类比法加模型验证，这在一定程度上能满足施工需求，但是对于变形控制要求严格，支护结构层次繁多的复杂深基坑，这种方法往往不能满足要求或者偏于安全。

本文针对实际工程中的问题，应用力学原理及数学原理对基坑支护结构进行简化，得到围护结构受力方程，再运用C++语言进行编程计算，得到结构受力优化后的支护位置，再通过有限差分软件FLAC3D建立三维模型，以台阶开挖模拟现场的坡面开挖，模型模拟结果与实测数据符合良好，并以此为基础建立优化对比方案，验证了优化方案的效果。

1 深基坑支护优化方法的提出

依据成都地铁某始发井对钢支撑轴力的监测结果来看，围护结构施加给支撑的作用力大小只是设计值的60%～70%，钢支撑由于承载强度不足而导致基坑发生破坏的情况在实际施工中较少，而因围护结构局部破坏导致的基坑整体失稳破坏则时有发生。在实际施工过程中，随着开挖深度加大，开挖临空面的增加，开挖的危险性也随之增大。而通常基坑工程一方面由于开挖过程通常为连续的流水施工，施工速度快，土体的应力释放不充分，另一方面基坑开挖完成后通常不会马上修筑结构体，而此时围护结构体在外部水土压力的作用下，所形成的位移变化是较大的，这一点在成都地铁2号线的实际监测中也有所反应;所以本文将重点分析开挖完成时，即基坑开挖到最底部时的围护结构受力，通过改变钢支撑的分布位置来改善围护结构的受力情况从而达到改善基坑围护结构变形，最终找到钢支撑的最适合支撑位置，从而实现对深基坑支护结构体系的优化设计，为基坑工程支护结构的设计提供一定的参考。

具体的优化设计方法的流程为:初步设计(依据假设支撑初始位置得到支撑能力)→优化设计(依据函数式得到支撑最优位置)→模拟验算(对再设计的支撑位置进行模拟验算)。

该优化方法具体来说可分为以下三点:

1)在初始设计中，为了更好地利用围护结构来承受荷载，尽量避免结构受力不均而导致的局部破坏，一般可以采用工程经验类比的支撑位置或者按等间距设置钢支撑进行初步设计，通过数值计算或者经验类比可以得到初步设计位置钢支撑的受力值Fi。

2)为了充分发挥结构的强度，减少结构体的侧移量，就必须使得结构的受力更为均匀，为了这一目标，通常可以采用两种方法:①使得结构体所承受的正负弯矩趋近相等;②使得结构体所承受的弯矩的方差趋近最小。以上两种优化方式均可以通过编制相应的C++或者Matlab程序实现。

3)最后依据得出的优化支护位置建立数值计算模型，对实际工程条件下钢支撑支护位置优化的效果进行数值模拟对比验算，找出最合理的钢支撑支护位置。

2 实际工程应用分析

2.1 工程概况

某地铁工程盾构始发井为明挖基坑，基坑深为14.0～17.5 m，宽为12～21 m。围护结构一般采用φ1200@2 200 mm的人工挖孔桩，盾构洞门处采用φ1500@1 800 mm的人工挖孔桩，桩顶上设1 200 mm×1 000 mm的冠梁，围护桩之间采用φ600 mm的钢管支撑(t=12，14 mm)，具体支护情况如图3所示。

根据钻孔勘探结果，在场地范围内上覆第四系人工填土，厚度为0.4～5.7 m，其下为粉质黏土，厚度为0.4～2.5 m;松散卵石土，厚度为0.5～4.0 m;稍密卵石，厚度为3.0～7.3 m;再次则为中密卵石，厚度为3.5～9.1 m;最后则为密实卵石。

2.2 基坑支护结构受力简化分析

该工程的整个支护结构采用外部人工挖孔桩+内部钢支撑的支护形式，沿基坑深度方向设置3道钢支撑。由于整个开挖过程中一直进行深井点降水，所以在计算分析时，没有考虑水压的影响。

在基坑的纵深方向取单位宽度围护结构，则可以把整个围护结构的实际受力情况简化如图1所示。

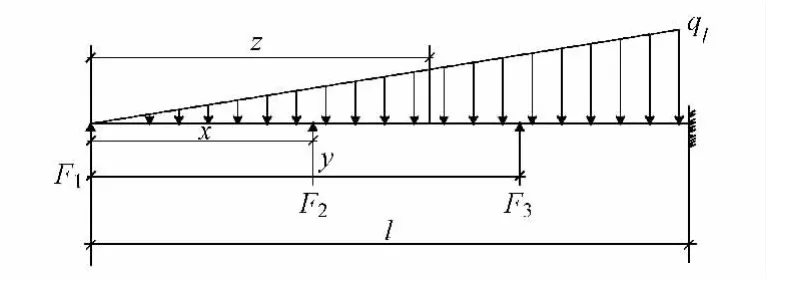
图1 基坑围护桩(墙)受力简化图式

根据上述简化的受力图1，可以得到围护结构的受力及其相应的限制条件为

式中:Fi表示对应位置的轴力设计值，根据实际测量结果，这里为了结构的安全储备量选取轴力设计值60%代入进行计算，kN;Mi表示对应于z处的横断面弯矩值，kN·m;x表示第2道钢支撑所处的位置，m;y表示第3道钢支撑所处的位置，m。

实际工程中围护桩的桩长18.5 m，桩尖埋深3.5 m，可选作为结构受力计算的桩长l为15 m，根据公式(1)用C++语言进行编程，可得支撑结构的3种弯矩状态(表1)。

表1 钢支撑结构的弯矩状态分析

将表1所得钢支撑位置参数代入到公式(1)，通过origin出图可以得到各支撑位置时对应的弯矩图，如图2所示。

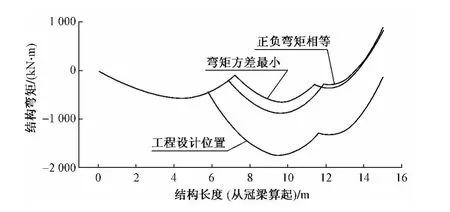
图2 三种弯矩状态弯矩分布

2.3 数值计算验证分析

为了对基坑开挖支护的一般情况进行分析，这里选取基坑开挖的某一典型区段进行开挖过程的模拟分析，模型实际选取断面如图3所示。

整个开挖工程采用有限差分软件FLAC3D进行模拟，模型具体尺寸为长×宽×高=97.8 m×16.0 m×68.0 m。由于在整个开挖过程中进行持续的降水，因此，在模拟过程中也没有考虑水压的影响。具体基坑支护模型如图4所示。

为了贴近实际的施工情况，模型采取逐层分步开挖的方法进行开挖，并及时进行喷射混凝土以及钢支撑的架设模拟，为了避免边界效应对计算结果的影响，这里对模拟结果数据的提取均选自模型中间某一断面数据，模型计算结果与实际监测结果的对比情况分别见图5及图6。

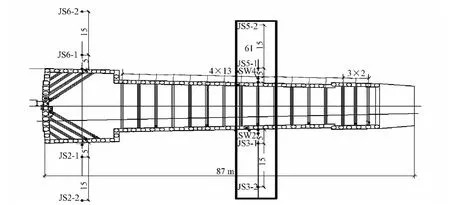
图3 模拟区间的选取示意(单位:m)

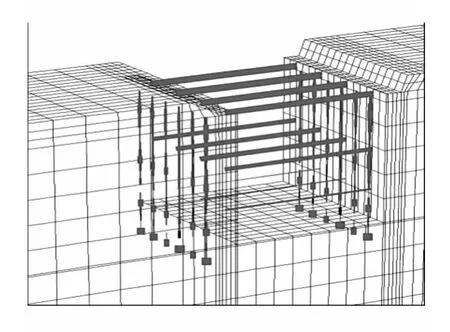
图4 基坑支护

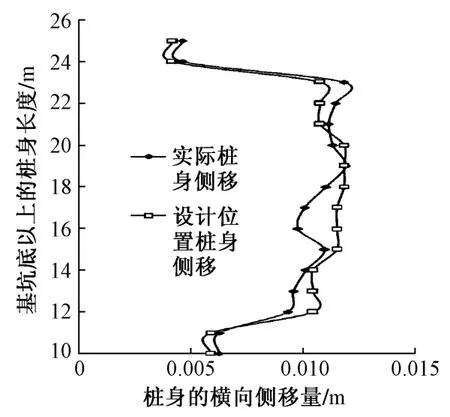
图5 设计位置与实际测量桩身侧移对比

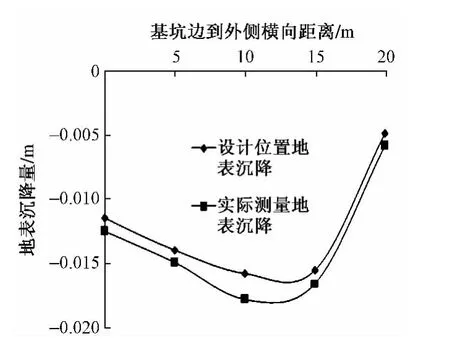
图6 设计位置与实际测量地表沉降对比

由图5、图6可以看出，按设计要求设置的钢支撑位置进行的数值模拟计算结果与实际开挖过程中监测的结果相比，两者桩身位移、地表沉降均比较符合，可以认为此时对设计位置的模拟即为对实际开挖过程的模拟。

为了对优化方法进行评价，将设计位置作为结构分析对比的参照标准。同时，为了对比分析更具有针对性，优化后的两种钢支撑位置的模拟只改变了支撑所在的位置参数，其他模拟参数均与设计位置保持一致，具体的模拟结果如图7、图8所示。

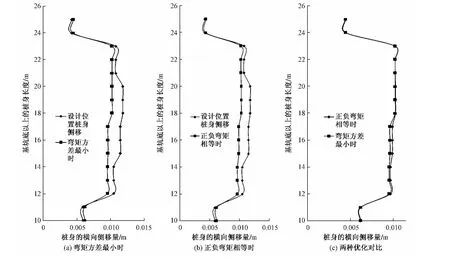
图7 三种支撑位置的围护结构横向位移

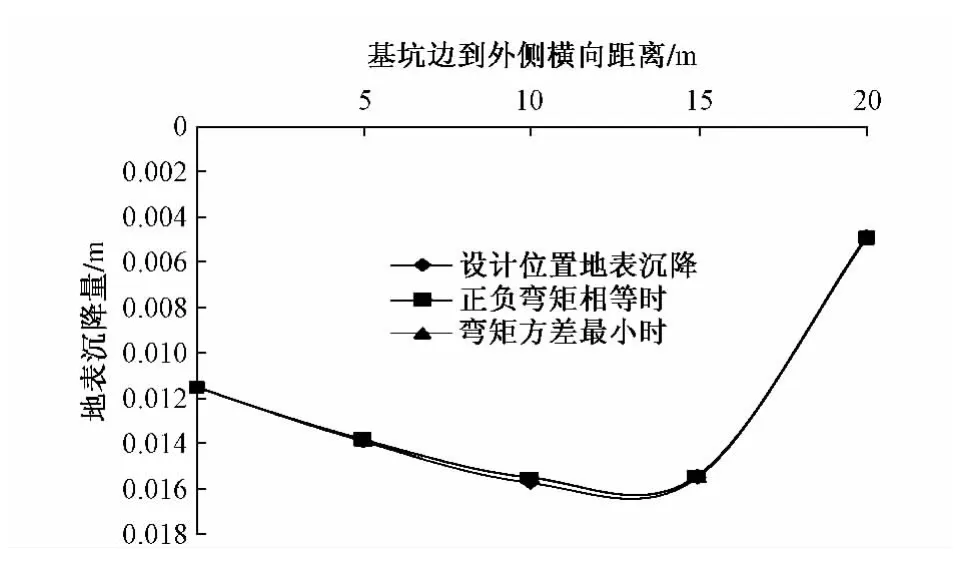
图8 三种支撑位置的地表沉降

从图7的对比中可以看出，当钢支撑的位置使得围护结构的正负弯矩相等时，围护桩结构本身的受力比设计位置更均匀，从而导致桩身的变形更协调，减小了桩身的总体侧移量，最大侧移量也由11.784 mm减少到10.253 mm，减少了近15%。从图8可以看出，钢支撑位置变化后的地表沉降几乎不变;计算还表明，正负弯矩相等时的桩顶沉降量也相差极小，可以看出对钢支撑位置的优化对基坑围护结构的变形起到很大的改善作用的同时，对于地表、桩顶沉降的影响极小。

通过表1选取弯矩方差最小时的支撑位置，此时由图2可以看出，围护结构的受力更为均匀。通过图7(a)可以看出随着桩身受力的进一步改善，桩身侧移进一步减小。

3 结论

本文通过对围护结构的受力计算分析，找到一种优化支撑支护的方法，使围护结构受力更均匀合理，更利于结构设计，同时也降低了桩身的侧移，改善了随后的施工净空条件，这对于一些对净空控制要求严格的深基坑开挖设计具有重要的参考价值。

［1］李启森，吴秀国，张厚美.盾构深基坑施工监测及分析［J］.隧道建设，2006，26(增 2):14-18.

［2］徐少平.成都砂卵石地层大型地铁基坑施工稳定性监测［J］.铁道建筑，2011(1):58-60.

［3］尹光明.城市隧道临近建筑物超深基坑支护理论与安全控制技术研究［D］.长沙:中南大学，2012.

［4］李晓芳.深基坑支护施工技术的研究与应用［D］.天津:天津大学，2008.

［5］王瑞科.深基坑支护结构变形的研究［D］.西安:西安建筑科技大学，2007.

［6］李琨，康健，商啸，等.城市复杂环境中深大基坑支护开挖施工技术［J］.建筑机械化，2011(增2):55-58.

［7］陈钟颐.土力学［M］.北京:清华大学出版社，1995.

［8］夏明耀.地下工程设计施工手册［M］.北京:中国建筑工业出版社，1999.

［9］谢李钊.深基坑现场实测及数值模拟［D］.长沙:中南大学，2009.