数值模拟脉动风场在斜拉桥抖振响应分析中的应用

李志国，何 能，廖海黎，段青松

(西南交通大学土木工程学院，四川成都 610031)

现代桥梁向大跨度的发展已成必然趋势，具有紊流特性的自然风会对柔性大跨度桥梁产生强迫作用，再加上桥梁结构在风荷载作用下本身自激力的耦合，会引起桥梁的抖振响应。抖振属于限幅振动，过大的抖振会引起行车的舒适性问题，长时间的抖振会导致桥梁结构的疲劳和构件的破坏，从而减少其使用年限。因此降低大跨度桥梁结构抖振响应的振幅，是桥梁设计必须考虑的评估问题。

工程中对大跨度桥梁抖振响应的评估是借助于风洞试验的方法完成的，即通过将相似的缩尺气弹模型在风洞中测得的紊流响应值换算成实桥值进行评估。但由于风洞试验成本高，周期长，再加紊流流场的等效模拟参数还存在技术的差异，使得这种半经验半理论的试验结果值只能作为一种很好的参考。抖振响应有限元计算方法可分为频域法和时域法两种，频域法对线弹性结构抖振响应分析比较简洁有效，但其不能考虑对风敏感的大跨度柔性桥梁结构的气动力等非线性问题。时域法是利用随机过程理论，将风荷载等效成时间序列下的气动力函数，并考虑结构自激力，进行时程分析，该法被众多学者在研究大跨度桥梁抖振响应时所采用［1-2］。

利用MATLAB编程方法，程序化模拟了数字风场样本［3］，再将风场样本等效为作用在桥梁结构有限元模型上的结点荷载函数，通过ANSYS时程分析得到某大跨度斜拉桥在紊流作用下的抖振响应，并将这种响应结果与频域法及风洞试验值对比［4］，得到了一些有益结论。

1 脉动风场数字化模拟及荷载等效

1.1 脉动风场数字化模拟

参考《公路桥梁抗风设计规范》顺风向脉动风谱选用圆频率表示的Simiu单边谱，见公式(1)。

竖向脉动风谱选用Panofsky单边谱，用圆频率表示见公式(2)。

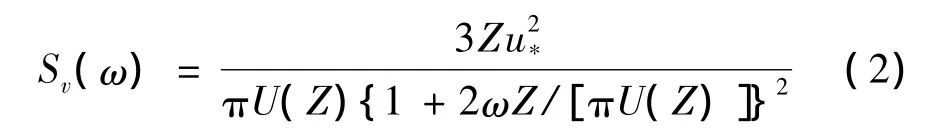
式中:ω为圆频率;u*为剪切速度，按照公式计算为结构周围建筑物平均高度，K≈0.4;U(Z)按照铅垂方向幂指数律计算，U(Z)=U10(Z/10)α，α为地表粗糙度系数。

利用谐波合成法(WAWS)［4］对n维风场进行选定风谱的平稳高斯随机过程模拟，其互谱矩阵见公式(3)。

对互谱密度函数矩阵S(ω)按照公式(4)进行Cholesky分解得到

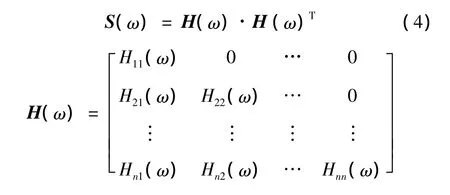
为了减少对S(ω)的分解次数来提高计算效率，对Hij(ω)按照公式(5)进行关于ω的分段拉格朗日插值运算

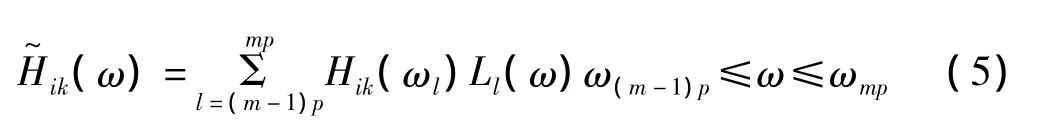
式中:m为频率分段数，p为插值点数，Ll(ω)为拉格朗日插值基函数。

从而，f(t)={f1(t)，f2(t)，…，fn(t)}T可以由公式(6)得到

式中:N为频率等分数，Δω为圆频率增量，ωkl为双索引频率，Φkl为随机相位角。

1.2 抖振力与自激力等效处理

风对桥梁的作用可分为平均风荷载的静力作用、脉动风荷载的抖振力作用和流固耦合的自激力作用。平均风荷载的静力作用可以线性叠加，不再累赘。抖振力按照气动导纳修正的Scanlan准定常气动力公式计算，对于桥塔、桥墩、拉索等只需考虑抖振力的阻力作用即可，见公式(7)。

式中:χ为气动导纳函数，C为三分力系数。

抖振力通过MATLAB程序实现［5］，用集中法将抖振力单元荷载等效为结点荷载。

自激力是在Scanlan颤振理论的基础上考虑三个方向位移对气动力的影响，用18个颤振导数表示，见公式(8)。

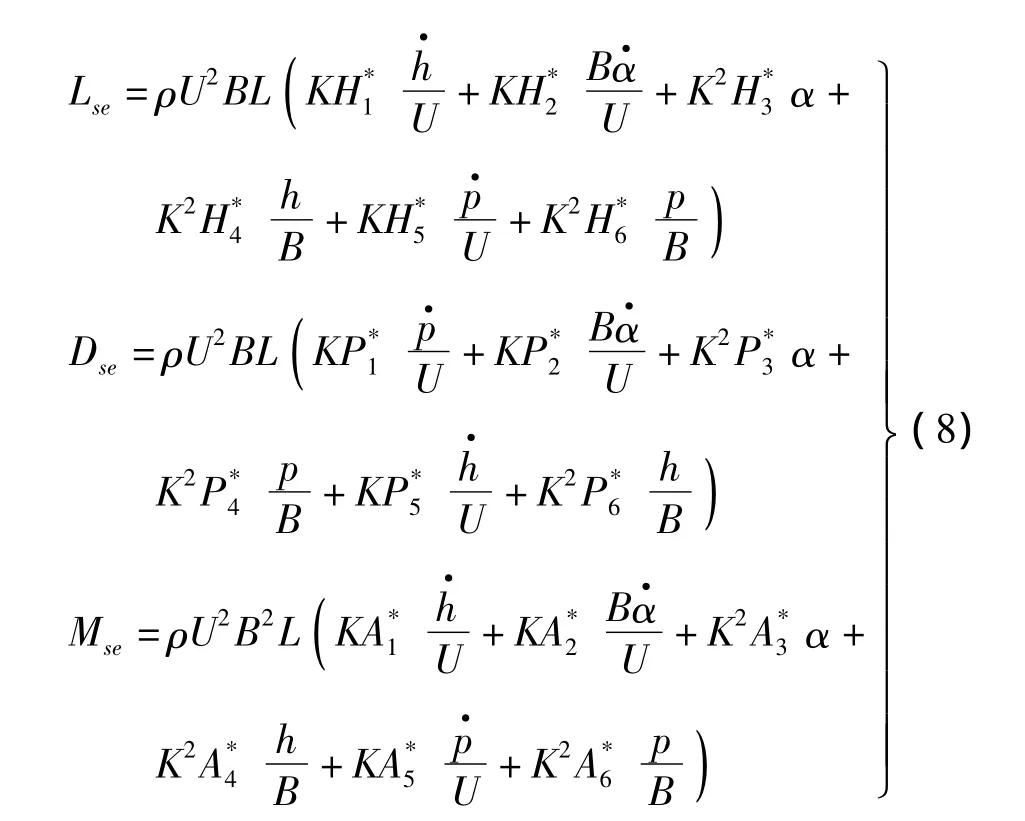
式中，H，P，A为颤振导数。

由上式可以看出自激力是h，p，α的函数，为了方便在ANSYS中计算，将自激力写成矩阵的形式

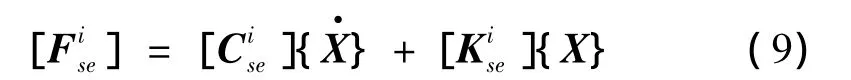
这样自激力的非线性可以在ANSYS中由气动阻尼和气动刚度表示的12个自由度的自定义单元MATRIX27单元来实现。

1.3 脉动风模拟及荷载等效流程

抖振时域法分析流程见图1。

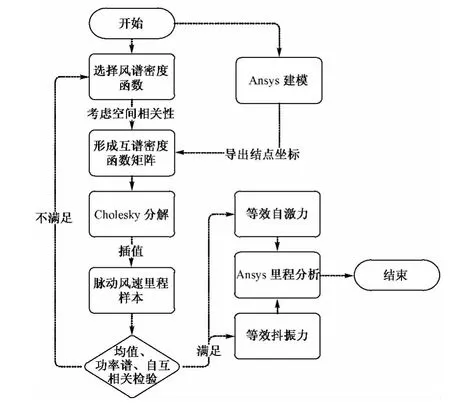
图1 抖振时域法分析流程

2 抖振响应分析实例

2.1 脉动风场模拟

将上述方法运用于某双塔斜拉桥，桥跨布置为(77+100+360+100+77)m。主梁采用预应力混凝土箱梁，主梁标准宽度为44 m。拉索采用空间双索面布置，锚固于主梁两侧。桥塔采用钢筋混凝土H型塔。桥跨布置如图2所示。对该桥有限元模型各个结 点处的脉动风时程模拟，模拟所需参数见表1。

图2 总体布置示意(单位:cm)

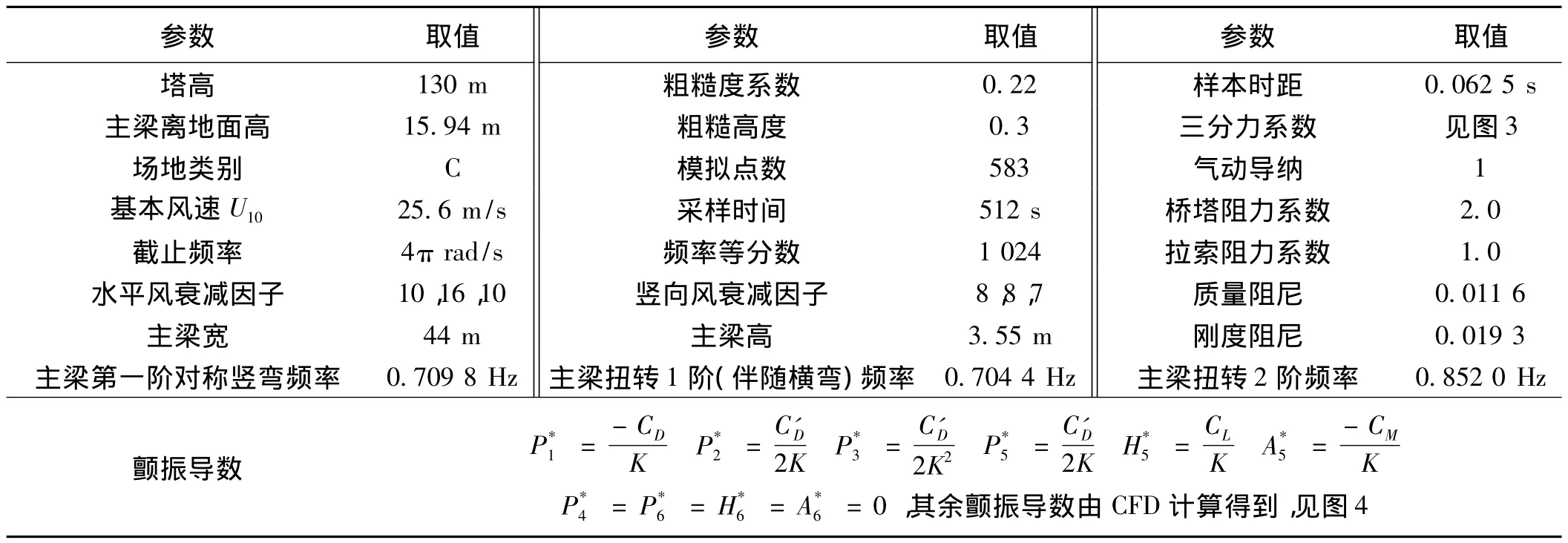
表1 脉动风场模拟及抖振计算的主要参数

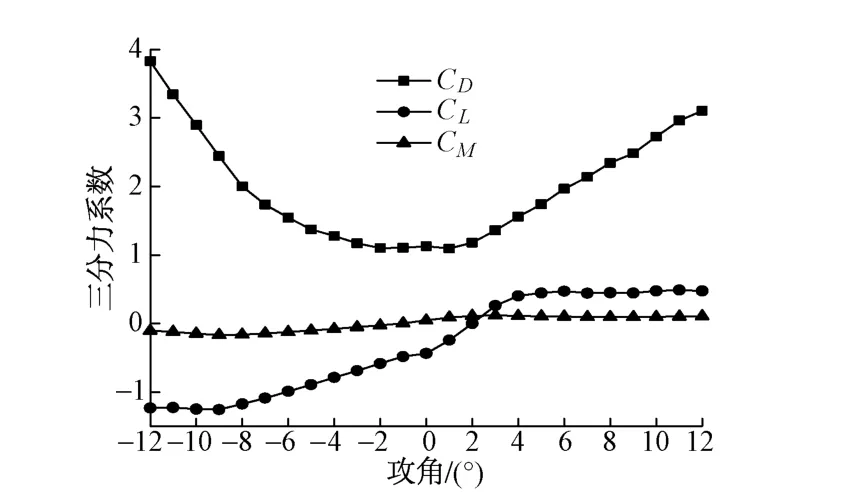
图3 三分力系数

图4 颤振导数

取跨中的59号点为检验点，对MATLAB的模拟结果进行分析。图5为59号点的水平y向脉动时程图，其均值均接近0(＜±0.2 m/s)。图6为59号点脉动风样本的功率谱密度与目标函数的吻合图，由图看以看出吻合较好［6］。

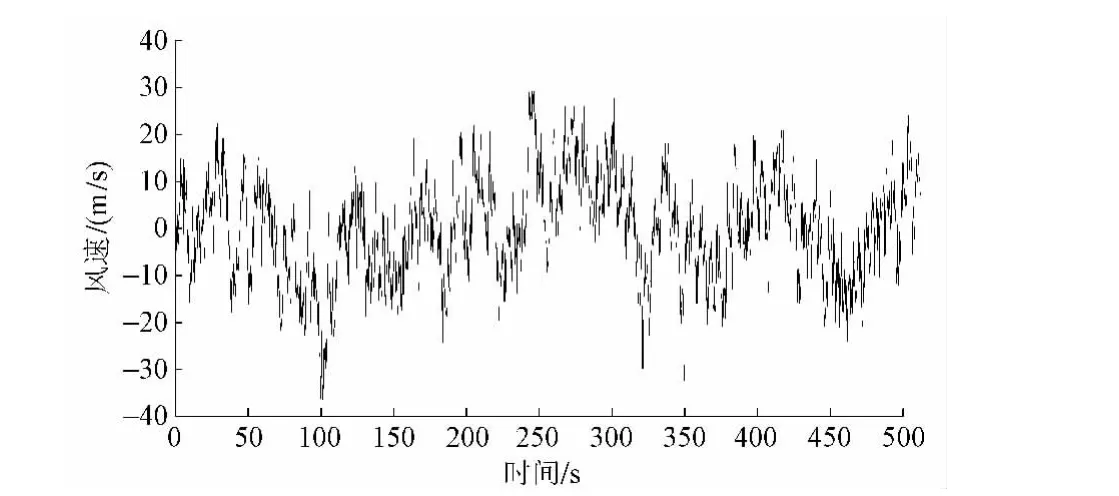
图5 59号点脉动风样本时程

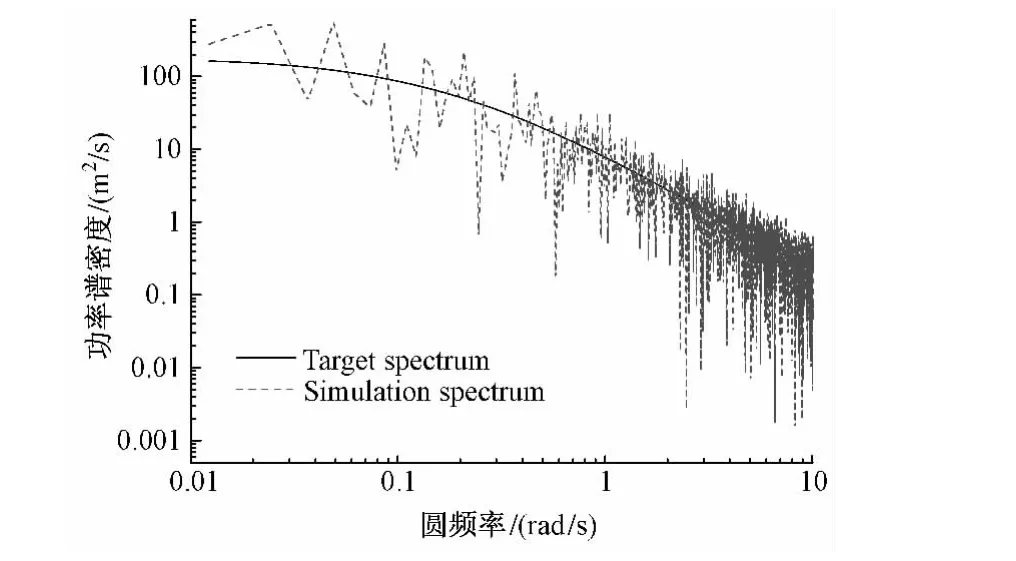
图6 59号点功率谱密度

2.2 抖振响应时域分析

对ANSYS计算的抖振响应结果分析，图7为59号点在竖向的抖振位移响应功率谱图，其响应频率与主梁竖弯基频吻合较好，当然59号点在横向和扭转向也有同样的结果。

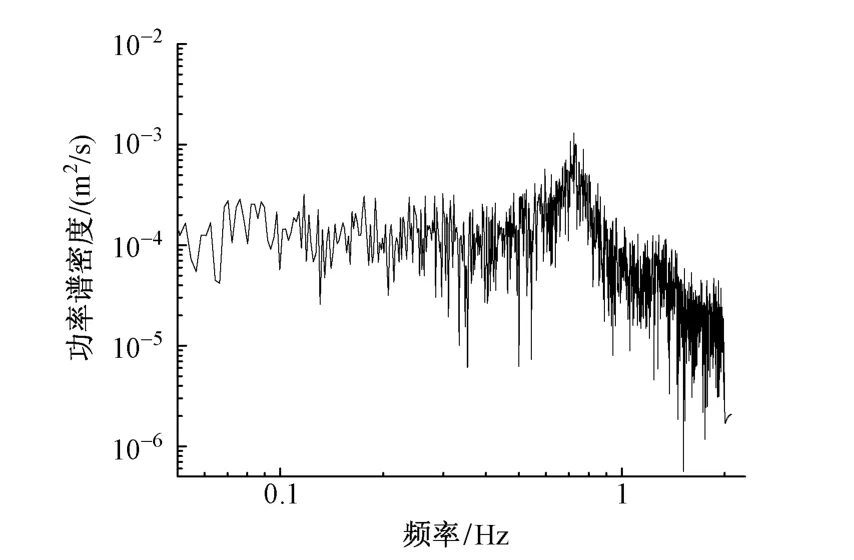
图7 主梁跨中59号点抖振位移响应功率谱密度

图8为不同时滞的主梁抖振振型，图中黑实线为主梁抖振响应位移均方根，其数值结果比频域法结果(方形虚线)偏高一点，主要是由于频域法忽略了非线性和高阶频率对抖振位移响应的贡献。从图中可以看出不同时滞横桥向的振动形态主要以第一阶正对称振型为主，但也不乏其他高阶频率的振型参与叠加。竖向和扭转就能很明显地观察出其高阶频率的贡献，这主要是由于脉动风荷载沿主梁方向的随机性及拉索和桥塔对振动形态影响较严重所致［7］。

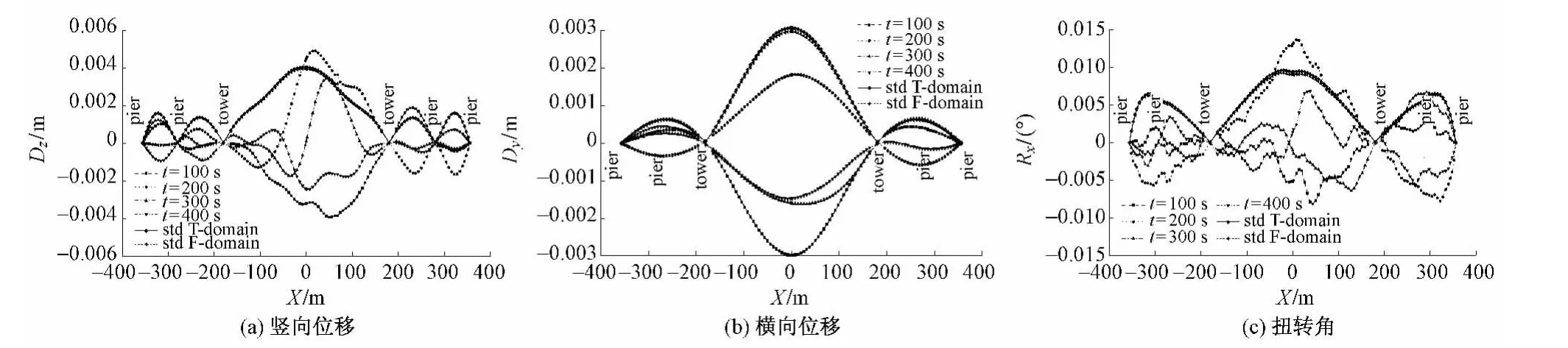
图8 主梁抖振位移响应

2.3 可靠性验证

为了验证本文方法的可靠性，在西南交通大学XNJD-3风洞中进行该桥全桥气弹模型对比试验。表2给出了部分计算结果与该桥风洞试验结果的对比。

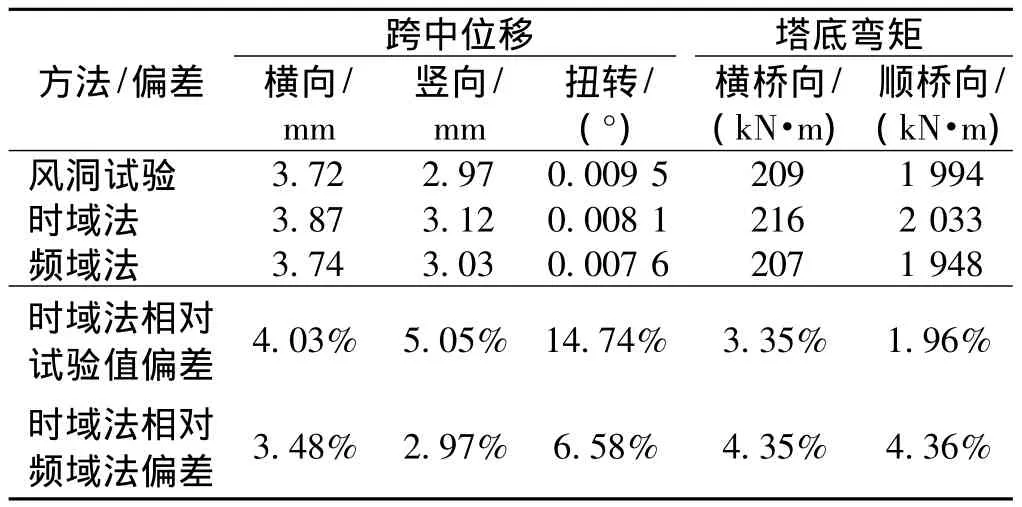
表2 计算与风洞试验结果比较

为了排除激光位移计及应变片的采集噪声，采用低通带滤波得到试验结果，进而忽略了高阶频率对风响应的贡献，再加上气弹模型相似度、风洞试验室的风场特性等因素造成抖振响应值有微小偏差，但总体与数值模拟方法计算结果吻合较好。

3 结论

在脉动风场的模拟和大跨度桥梁抖振响应时域分析方法的研究中可以得到如下结论:

1)利用谐波合成法，选择恰当的功率谱密度函数、时间步长、截止频率、模拟时长和插值方法等就可以有效获得好风场样本［8］。

2)相比于频域法，用时域法对大跨度桥梁抖振响应分析可以考虑几何非线性和气动力非线性，并可以考虑高阶频率对抖振响应的贡献。

3)桥梁抖振响应通常以低阶频率贡献为主，但也不能忽略高阶频率对抖振响应的参与。时域法就能很好地反映高阶频率对抖振响应的贡献。

4)通常情况下，时域法对抖振响应的分析结果偏保守，要比频率法稍大。

经过实例计算分析并与频域法和风洞试验结果比较，本文所采用的数值模拟风场时域法计算桥梁抖振响应的方法是可行的。

［1］丁泉顺，陈艾荣，项海帆.大跨度桥梁空间脉动风场的计算机模拟［J］.力学季刊，2006(2):184-189.

［2］曹映泓，项海帆，周颖.大跨度桥梁非线性颤振和抖振时程分析［J］.广东公路交通，2000(增1):38-42.

［3］骆宁安，杨文武，韩大建.大跨度桥梁脉动风场的随机模拟［J］.华南理工大学学报:自然科学版，2002(3):57-83.

［4］李永乐，廖海黎，强士中.桥梁抖振时域和频域分析的一致性研究［J］.工程力学，2005，22(2):179-183.

［5］胡亮，李黎，彭元诚.大跨桥梁抖振时域分析的程序化方法［J］.中国公路学报，2006，19(6):59-64.

［6］李黎，胡亮，樊剑.具有桥塔风效应的桥梁风场数值模拟［J］.振动与冲击，2007，26(5):14-19.

［7］李永乐，周述华，强士中.大跨度斜拉桥三维脉动风场模拟［J］.土木工程学报，2003(10):60-65.

［8］葛耀君.大跨悬索桥抗风［M］.北京:人民交通出版社，2011.