城市轨道交通桥梁振动及噪声辐射研究
王小宁,张 楠,孙 奇
(北京交通大学土木建筑工程学院,北京 100044)
目前我国轨道交通实行“以桥代路”的策略,高速铁路中桥梁比例很大,城市轨道交通也广泛采用高架结构,由城轨桥梁振动产生的噪声问题越来越突出。
噪声的来源有轮轨、动力系统、车辆非动力系统、高架轨道结构等。研究结果表明,噪声的低频成分(<250 Hz)主要由于桥体结构振动辐射产生,而轮轨振动辐射是高频噪声(250~1 000 Hz)的重要来源。刘林芽等[1]基于简化的二维模型,应用边界元方法对噪声场进行研究,为轻轨高架声学环境设计和噪声治理提供了重要参考。朱怀亮等[2]研究了上海共和新路地铁双层高架轨道交通所引起的振动和环境噪声问题。高飞等[3]应用声学理论建立列车通过高架桥梁时的噪声预测模型,对由结构噪声和轮轨噪声引起的高架结构附近的噪声传播规律进行了研究。张鹤等[4]结合车桥耦合振动理论和声传播理论,建立了桥梁振动辐射瞬态噪声的有限元—边界元混合求解模型,对一座三跨钢连续梁桥在交通荷载作用下桥梁振动产生的瞬态噪声场进行了试验分析和数值模拟。李晶等[5]利用有限元软件 ANSYS 与 LMS Virtual.Lab Acoustics对城市轨道交通高架桥梁的振动声辐射进行了分析。王巧燕等[6]对上海轨道交通1号线和明珠线地面段和高架段列车加速出站、站间匀速行驶以及减速进站时的噪声进行了采样分析。目前对不同梁型振动引起的噪声辐射问题研究得还很少。
本文利用ANSYS建立槽型梁、箱型梁及T型梁3种不同梁型的简化模型,采用移动荷载列模型作为初始激励,分析3种梁型的振动响应。以计算得到的振动响应作为声学模型的边界条件,用声学边界元方法分析3种梁型振动产生的声场在时域和空间上的分布规律。
1 城轨桥梁振动有限元分析
1.1 有限元振动计算理论
在有限元分析中,本文采用瞬态动力学分析结构的动力响应,得到在随时间变化的荷载作用下结构节点位移、应力、速度、加速度等的响应。瞬态动力学分析也称为时间历程分析,其基本运动方程为
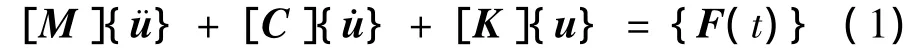
式中:[M],[C],[K]分别为质量、阻尼和刚度矩阵;分别为节点加速度、速度和位移向量;{F(t)}为节点荷载向量。
结构的阻尼采用瑞利阻尼,即

式中,α为质量阻尼系数,β为刚度阻尼系数。根据振型正交条件,待定常数α和β与振型阻尼比之间应满足以下关系式

式中,ωi和ωj分别为结构的第i阶和第j阶固有频率,ξi和ξj为相应于第i阶和第j阶振型的阻尼比。
进行结构动力分析时,荷载向量是已知的,并采用无条件稳定的Newmark-β法进行积分计算。Newmarkβ法假设在时刻t和t+1时,系统的加速度分别为和,时段的长度为Δt。基于Newmark-β法的假定,在该时间段内的t+τ时刻系统的加速度、速度和位移满足下面的关系式
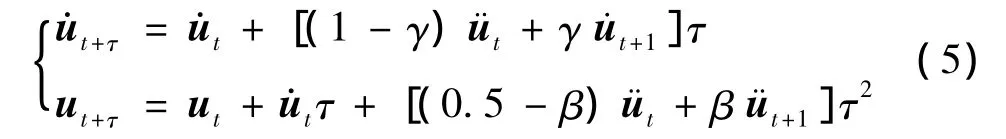
式中,γ和β是由积分精度和稳定性决定的参数。
通过调整参数γ和β,可以适应不同的要求,因此Newmark-β法是一种比较灵活的算法。在动力分析时,对结构的动力响应起决定性作用的往往是低阶振型,因此可只关注几个低阶响应就可以获得满足精度要求的解,此种情况下要求算法是无条件稳定的。在无条件稳定的算法中,积分步长Δt只需满足精度的计算要求,不必考虑稳定性。在实际分析中,这一点会显著减少计算工作量。在波传动问题上,或在离散系统问题上,如果只考虑最低的几个频率,计算结果会产生较大的误差。由此可见,不同的问题对算法有不同的要求。当γ<0.5时,会出现人工负阻尼,系统由于自激失去稳定性;当γ=0.5时,无人工阻尼,能得到准确的高阶响应;γ>0.5时,Newmark-β法具有“数值阻尼”的机理,可以用来衰减高频分量,但在衰减高频分量的同时,低阶振型的分量也受到了过多的影响,并且γ>0.5时,Newmark-β法只有一阶精度,而数值积分至少应具有2阶精度。由于以上的原因,Newmark-β法中一般不利用γ>0.5的振幅衰减作用,通常取γ=0.5。在分析复杂的有限元系统时,要求逐步积分法是无条件稳定的,否则在积分过程中,结构的高频分量的反应会无限制地增长,从而使整个积分失去意义。因此一般取β=0.25,γ=0.5,这时Newmark-β法是无条件稳定的,也是最常用的。
1.2 城轨桥梁结构的有限元模型
3种城轨桥梁的跨度都为32 m,其余参数如下:
槽型梁的上翼缘宽度1.80 m,厚度0.72 m;底板宽度10.00 m,厚度0.70 m;腹板高度2.30 m,厚度0.60 m。
箱型梁为单箱单室梁,其上翼板宽度12 m,厚度0.44 m;底板宽度6.00 m,厚度0.28 m;腹板高度2.58 m,厚度0.45 m。
T型梁由4片 T梁构成,其单片上翼板宽度3.00 m,厚度0.24 m;腹板高度2.18 m,厚度0.21 m。
城轨桥梁采用Shell63单元模拟,分析中采用的模型材料密度为2 500 kg/m3,泊松比为0.2。为了使不同城轨桥梁截面的惯性矩一样,3种城轨桥梁采用不同的弹性模量,槽型梁弹性模量为3.55×1010N/m2,箱型梁弹性模量采用4.18×1010N/m2,T型梁弹性模量采用8.00×1010N/m2。利用有限元软件ANSYS建立3种城轨桥梁的几何模型,并对其进行网格划分,得到对应城轨桥梁的有限元模型。
1.3 城轨桥梁结构的动力响应
文献[7]采用移动荷载模型分析轨道交通桥梁的动力响应,与实测数据对比结果表明采用移动荷载模型分析精度是足够的。因此本文选择6节车辆编组(1拖+4动+1拖)移动荷载列作为模型的初始激励。移动荷载列模型如图1所示。

图1 移动荷载列(单位:m)
对模型施加初始激励,以列车的行驶速度V=350 km/h为例,得到各个城轨桥梁跨中节点位移响应时程曲线,如图2所示。
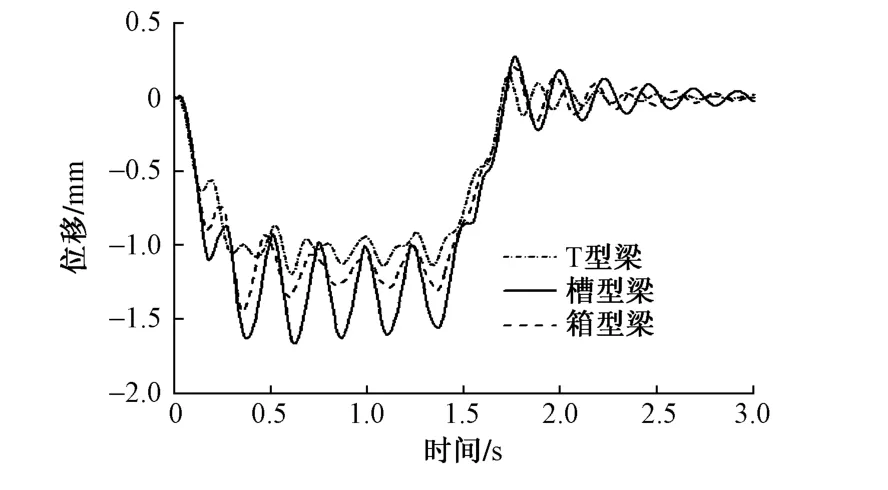
图2 城轨桥梁跨中节点位移响应时程曲线
由图2可知:在移动荷载列的作用下,槽型梁跨中节点位移最大,其值为1.66 mm,其次是箱型梁,为1.45 mm;最小的是T型梁,为1.20 mm。
2 城轨桥梁振动噪声辐射数值计算
2.1 振动辐射计算理论
图3表示声压场的积分和求解域,Y表示场点,X表示源点,Γ表示声传播边界,n表示边界Γ上的法线方向,Ω表示空间求解域。

图3 声传播问题的积分和求解域
在均匀的理想流体介质里,小振幅声波声压p的三维波动方程即为空气中以声压p为变量的声波控制方程

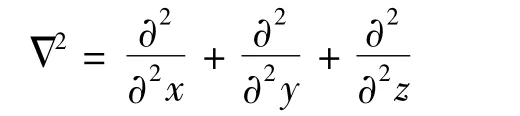
假设p*(Y,t)为波动方程的基本解,基本解在空间域Ω、时间域T满足基本控制方程,则瞬态声场的控制方程可以利用声压或者速度势函数表示
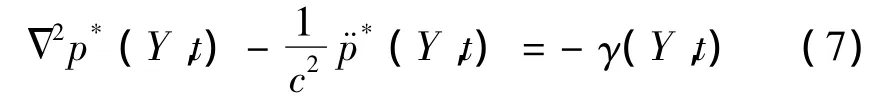
式中,γ(Y,t)为空气波介质中的源密度函数。

式中,δ(t-τ)与δ(Y-X)为delta函数。
声传播问题的边界条件描述声传播边界Γ上声压和结构表面响应之间的关系。定义q=∂p/∂n为声通量,则可描述传播边界Γ的边界条件

瞬态声压计算是在时间域求解声辐射的方程,需要定义初始条件,t=0时刻S1与S2初始状态的声压p0和声压关于时间的一阶导数v0分别为
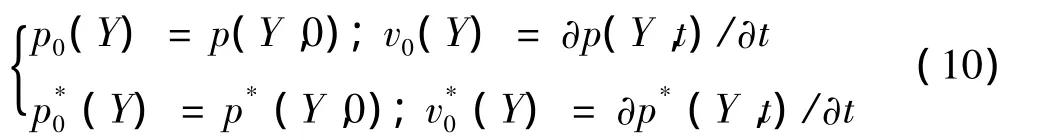
根据式(6)、式(9)、式(10),并利用 delta函数的性质,通过Laplace变换和逆变换,可以求得声波时域计算的边界积分方程
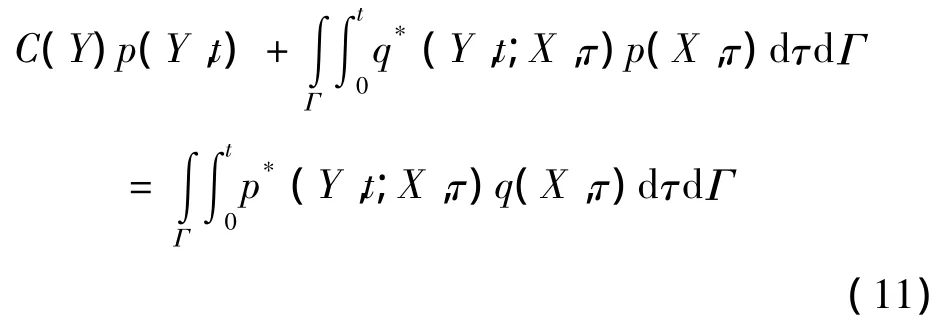
式中,C(Y)为边界表面的形状几何参数,p*(Y,t;X,τ)为声压在场点Y的基本解。
对三维空间和时间域实现边界积分方程式(11)的求解,需要采用数值方法,对时间和空间分别进行离散。
域Ω中各点的声压由边界Γ上的声压和声通量求得,振动声辐射问题中,已知结构的振动响应(位移、速度、加速度),可以得到结构边界上各节点的声通量,已知声通量可以得到边界上所有节点的声压。获得结构边界上各节点的声压和声通量之后,可计算得到声场中各点声压。
本文数值模拟中假定桥面板周边的空气振动与桥面板的振动一致,重合的节点具有相同的边界条件,因此知道了固体边界上的位移响应结果,就可以计算声场边界上的声压,进而求得整个声场中任意一点的声压。
2.2 城轨桥梁声学模型及对应场点布置
在软件LMS Virtual.Lab Acoustics模块中边界元法与声学有限元相比有很大的灵活性,边界元法既可以计算封闭空间中的声场,也可以计算非封闭空间的声场。声学有限元只能计算封闭空间内的声场。如果要计算非封闭空间的声场,需采用声学无限元法。本文采用的是软件中的间接边界元方法计算城轨桥梁的振动辐射声场。
LMS Virtual.Lab Acoustics中利用瞬态边界元方法求解时,如果计算振动引起的辐射声场,只能以振动位移作为初始条件,且声学边界元网格必须是三角形网格。为了满足计算的精度要求,边界元网格的最大边长L应满足

式中,fmax为最大频率。
桥梁的频率响应主要在100 Hz以下,本文采用的单元边长为0.5,满足上述公式要求。利用ANSYS建立城轨桥梁的边界元模型以及要研究的场点网格模型,保存为CDB格式的文件。
取跨中截面为研究对象,在跨中截面处的场点上选取10个点研究各个城轨桥梁声场分布特性,场点布置如图4所示。
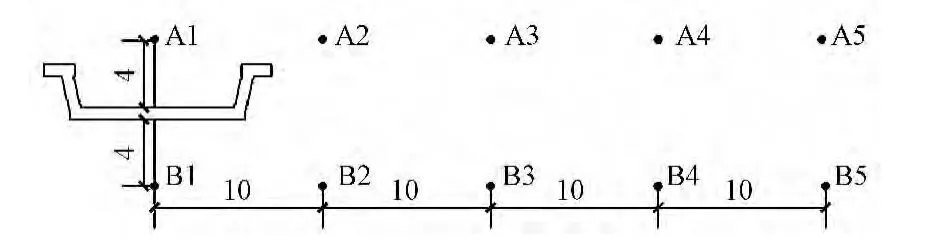
图4 槽型梁布置场点示意(单位:m)
箱型梁及T型梁的场点布置和槽型梁的场点布置一样,不同的是箱型梁和T型梁的基准面是上翼缘板,而槽型梁场点布置的基准面是底板。
2.3 城轨桥梁振动辐射噪声计算
利用ANSYS对有限元模型进行动力响应分析,已经得到模型各个节点的位移响应时程,节点的响应结果保存为RST格式的文件,将其作为城轨桥梁声学模型的初始边界条件,对城轨桥梁的瞬态辐射噪声进行分析。
利用LMS Virtual.Lab声学模块数值模拟分析得到各场点最大声压级如表1所示。

表1 辐射噪声最大值 dB
由表1可得出以下结论:
1)计算场点的声压级最大值在73.47~100.69 dB。由于大地反射作用的影响,除箱型梁上部A1,A4,A5场点声压级大于其对应下部场点B1,B4,B5的声压级外,城轨桥梁的其余下部场点的声压级均大于其对应上部场点的声压级。
2)场点距离为40 m时,槽型梁场点声压级衰减幅度最大,上部场点及下部场点衰减幅度分别为21.23 dB和26.54 dB;其次为箱型梁,其上部场点及下部场点衰减幅度分别为18.22 dB和16.44 dB;T型梁场点声压级衰减幅度最小,其上部场点及下部场点衰减幅度分别为13.98 dB和16.69 dB。
3)场点距离为40 m时,槽型梁场点声压级衰减速率最快,随着距离跨中截面越来越远,其衰减速率呈递减趋势;T型梁场点的声压级衰减速率最小,但随着距离跨中截面越来越远,其衰减速率变化范围不大;箱型梁上部场点声压级衰减速率随距离增加呈递减趋势,但上部场点的声压级衰减速率呈先增大后减小的趋势。
3 列车运行参数对结构振动及噪声辐射的影响
城轨桥梁的结构振动噪声辐射与梁上列车的运行参数有密切关系,本文对 150,200,250,300 和350 km/h共5种速度下的结构振动和噪声辐射进行了探讨,并研究了单线行驶和双线对开行驶条件下城轨桥梁结构的振动和噪声辐射。各城轨桥梁跨中节点的位移响应最大值如表2所示。

表2 跨中节点位移最大值
由表2可知:
1)单线行驶工况下,位移在1.10~1.66 mm。槽型梁跨中节点的位移最大,其次为箱型梁,T型梁的位移最小。3种城轨桥梁的位移都随列车行驶速度的增加而增加。箱型梁在速度为200 km/h时,位移有突变现象。
2)双线行驶工况下,城轨桥梁位移的幅度变化范围为2.21~2.89 mm,随着列车行驶速度的增加,T型梁的位移呈递增趋势,槽型梁和箱型梁的位移呈波浪形变化,总体上呈现增大趋势。速度为300 km/h时槽型梁的位移大于箱型梁,其余行驶速度条件下,箱型梁的位移最大,其次为槽型梁,T型梁的位移最小。
以不同工况条件下的位移作为边界元模型的初始边界条件,导入到LMS Virtual.Lab的声学模块中计算3种城轨桥梁的振动噪声辐射,噪声的评价区域一般集中在桥梁的下方,因此主要选取桥梁下方的场点进行统计,场点声压级计算结果统计如表3~表5所示。
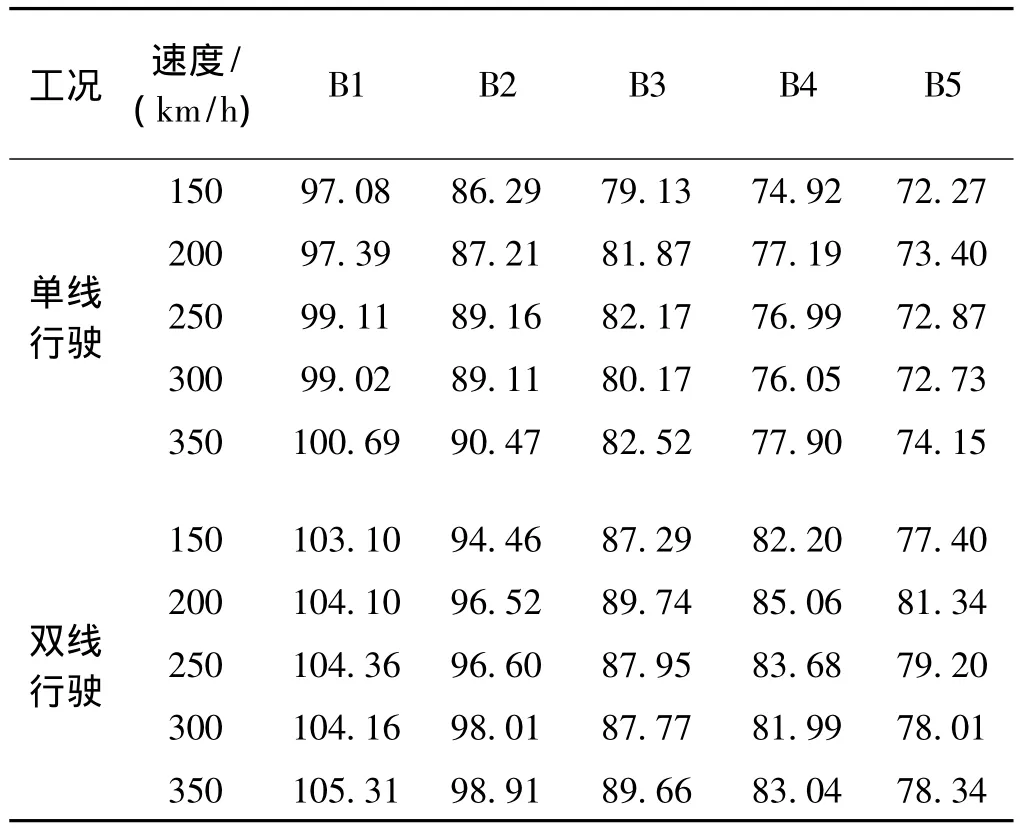
表3 槽型梁场点声压最大值统计 dB

表4 箱型梁场点声压最大值统计 dB

表5 T型梁场点声压最大值统计 dB
由表3~表5可知:随着列车行驶速度的增加,3种城轨桥梁的场点声压级呈波浪形变化,总体呈增加趋势。相同速度下,双线行驶比单线行驶时场点声压级大,槽型梁场点声压级增加幅度在4.14~9.31 dB,箱型梁的增加幅度在0.80~6.15 db,T型梁的增加幅度在1.22~6.15 db。与单线行驶相比,双线行驶对槽型梁的影响最大,其次为T型梁,对箱型梁的影响最小。
4 结论
1)在列车荷载作用下,槽型梁跨中节点的位移最大,其次为箱型梁,T型梁的位移最小。随着列车行驶速度的增加,3种城轨桥梁的位移响应均增加。槽型梁的增加幅度最大,其次为箱型梁,T型梁的增加幅度最小。与单线行驶工况相比,双线行驶工况下槽型梁受到的影响最大,其次为T型梁,箱型梁受到的影响最小。
2)由于大地的反射作用及城轨桥梁截面形式的不同,场点声场的空间分布是不同的。下部场点的声压级普遍大于对应的上部场点的声压级。场点距轨道中心线0~10 m范围内,槽型梁的场点声压级最大,其次为T型梁,箱型梁的场点声压级最小。场点距轨道中心线10~40 m时,T型梁的场点声压级最大,其次为箱型梁,槽型梁的场点声压级最小。随列车行驶速度的增加,3种城轨桥梁的场点声压级呈波浪形变化,总体呈增加趋势。同等速度条件下,双线行驶比单线行驶时场点声压级大,双线行驶工况对槽型梁的影响最大,其次为T型梁,对箱型梁的影响最小。
3)工程实际中研究结构振动噪声辐射时,将有限元软件ANSYS和LMS Virtual.Lab声学模块相结合可以快速预测结构的振动响应和相应的振动噪声辐射,基于减震和降噪的目的可以选择不同截面形式的城轨桥梁或对列车的运行速度进行控制。
[1]刘林芽,雷晓燕.轮轨噪声的预测[J].铁道学报,2004,26(2):101-104.
[2]朱怀亮,袁二娜,李鹏,等.城市立体轨道交通的环境噪声测试与分析[J].上海大学学报,2009,15(6):611-614.
[3]高飞,夏禾,安宁.北京地铁5号线高架结构的辐射噪声分析与实验研究[J].中国铁道科学,2010,31(5):134-139.
[4]张鹤,谢旭,山下夫.交通荷载引起的钢箱梁桥振动辐射瞬态噪声评估[J].振动工程学报,2011,24(3):221-227.
[5]李晶,张楠,张立彬.高架桥梁振动与结构噪声数值模拟[J].环境工程,2012,30(增):156-160.
[6]王巧燕,翟国庆,朱艺婷,等.不同行驶条件下轨道交通噪声频率特性比较研究[J].噪声与振动控制,2008,28(2):85-87.
[7]高传伟,唐雅茹,余华.基于移动荷载过桥的轨道交通桥梁振动研究[J].中国铁道科学,2005,26(2):73-76.

