高速铁路道岔平面设计参数与侧线线型的研究

王树国，葛 晶，孙家林，王 猛

(中国铁道科学研究院，北京 100081)

高速铁路道岔平面设计参数与侧线线型的研究

王树国，葛 晶，孙家林，王 猛

(中国铁道科学研究院，北京 100081)

根据我国道岔设计、试验和运营实践经验提出高速铁路道岔平面设计参数与动力学评价指标，依据选定的平面设计参数，设计了18号和42号道岔侧线线型。使用NUCARS建立了车辆—道岔耦合动力学模型，利用该模型计算了动车组侧向通过道岔的动力学响应。计算结果表明：高速铁路平面设计参数与动力学评价指标的选取及18号道岔和42号道岔的线型是合理的。

高速铁路道岔 平面设计参数 侧线线型 动力学模型

1996年我国设计研发了18号和30号道岔，但均采用单圆曲线线型。秦沈客运专线38号道岔侧线采用圆曲线+缓和曲线线型，导曲线半径为3 300 m，是我国首次设计、制造和批量使用侧线采用缓和曲线的道岔［1-2］。18号和42号道岔直向通过速度为300 km/h，其中18号道岔采用单圆线线型，42号道岔采用圆曲线+缓和曲线线型［3-5］。为保证道岔高平顺性和旅客乘坐舒适性，确定了我国高速铁路道岔的平面设计参数，设计了侧线线型，并运用动力学仿真技术进行了理论验证。

1 平面设计参数与动力学评价指标

1.1 平面设计参数［6］

根据我国道岔设计、实车试验经验和运营实践，选定高速铁路道岔的平面设计参数如下：

1)未被平衡的离心加速度α≤0.5 m/s2(欠超高75 mm)。

2)未被平衡的离心加速度时变率ψ≤0.4 m/s3(欠超高时变率60 mm/s)，圆曲线尖轨尖端除外。

3)18号道岔与岔后附带曲线间的夹直线长度及用于渡线的2组18号道岔间的夹直线长度不应小于20 m。渡线道岔的两支反向缓和曲线起点间可直接连接或插入任意长度的直线段。

1.2 动力学评价指标

根据道岔实车试验与运营实践经验选定车辆—道岔动力学性能评价指标如表1所示。其中，轮重减载率是指采用间断式测力轮对测试并计算出的试验参数，采用连续式测力轮对测试的轮重减载率一般要求不大于0.65［7］。车体横向和垂向加速度一般受列车侧向过岔控制，要求分别不大于1.5 m/s2和2.0 m/s2，列车直向过岔量值较小，上述指标一般不会超过1.0 m/s2和1.5 m/s2。另外，道岔本身的动力响应还应包括道岔磨耗指数、轮轨接触动应力等。

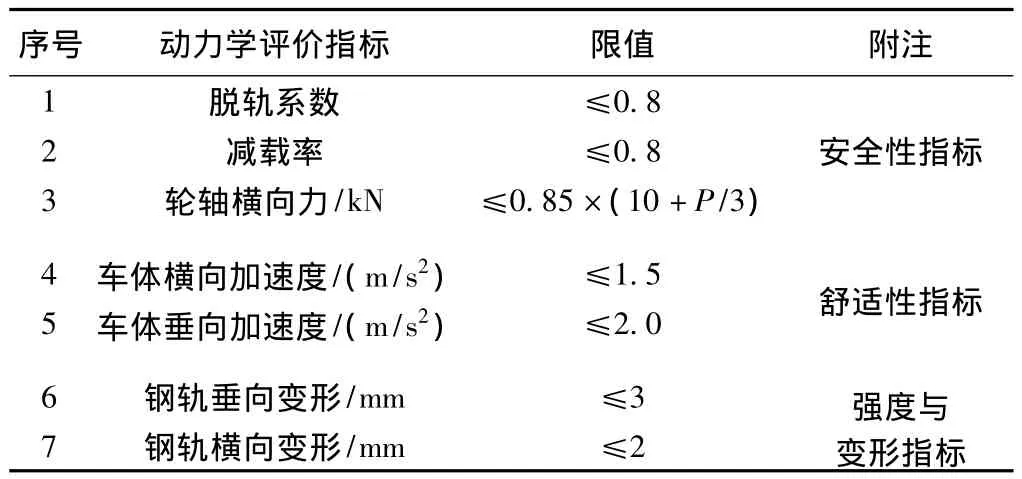
表1 车辆—道岔动力学性能评价指标

2 车辆—道岔耦合动力学模型

2.1 车辆模型

采用多体动力学的思想，使用NUCARS软件对我国高速动车组CRH2-300建模，把车辆离散成15个刚性体，最终建立了具有86个自由度的动车组CRH2-300客车—轨道非线性耦合动力学模型。这86个自由度分别为车体和前、后构架以及8个轴箱的纵移、横移、沉浮、侧滚、点头与摇头共66个自由度;4个轮对的纵移、横移、沉浮、侧滚与摇头共20个自由度。各个刚体之间使用NUCARS提供的连接单元进行建模，共建立轮对与轴箱、构架与轴箱、车体与构架以及轮轨连接56对，并定义了这些连接的特性。

2.2 道岔模型

为了精确描述转辙器和辙叉区钢轨件的不同顶面轮廓形状，将转辙器离散为8～12个断面，辙叉离散为4～8断面，列出道岔各个断面的离散点数据，通过NUCARS提供的CFIT/WRCON程序拟合，可以得到这些离散点上的道岔顶面轮廓形状，离散点间的顶面轮廓形状通过线性内插法得到，从而保证了道岔区模型模拟的真实性。

道岔模型中采用的基本假定如下：

1)尖轨与基本轨密贴段，两钢轨共同承受着列车荷载，假定两者位移相同，将该处两钢轨视为1股。该钢轨视为弹性地基支承基础上的变截面欧拉梁，道岔区内其它部分钢轨视为弹性地基支承基础上的等截面欧拉梁。

2)列车直向过岔时，不考虑曲尖轨的参振;列车侧向过岔时，不考虑直尖轨的参振。

2.3 轮轨接触模型

由于道岔区钢轨断面变化复杂，可能发生多种轮轨接触方式。充分考虑轮轨接触的变化特点是仿真模拟的关键。仿真计算采用NUCARS提供的轮轨渗入接触模型，只需要输入轮轨廓型，接触关系实时计算，可以准确地模拟岔区复杂的轮轨多点接触。

3 18号道岔侧线线型与夹直线长度设计及其仿真计算

3.1 18号道岔侧线线型设计及其仿真计算

18号道岔主要平面参数见表2。

表2 18号道岔主要平面尺寸

利用建立的动车组—道岔动力学仿真模型，对高速铁路18号道岔的动力响应进行仿真计算。当动车组CRH2-300以80 km/h侧逆向通过18号道岔时，车体横向加速度、脱轨系数、轮重减载率、轮轴横向力动力响应时程曲线如图1～图4所示。

从车辆运行舒适性来看，车体垂、横向振动加速度最大值分别为0.38 m/s2和0.62 m/s2，＜1.0 m/s2的限值要求;从车辆运行安全性来看，脱轨系数、轮重减载率最大值分别为0.18和0.22，均＜0.8的限值要求。

3.2 18号道岔夹直线长度及其仿真计算

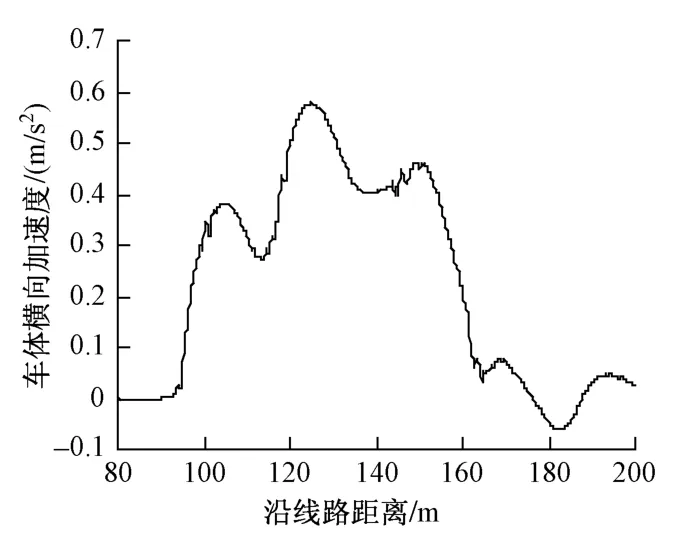
图1 车体横向加速度时程曲线

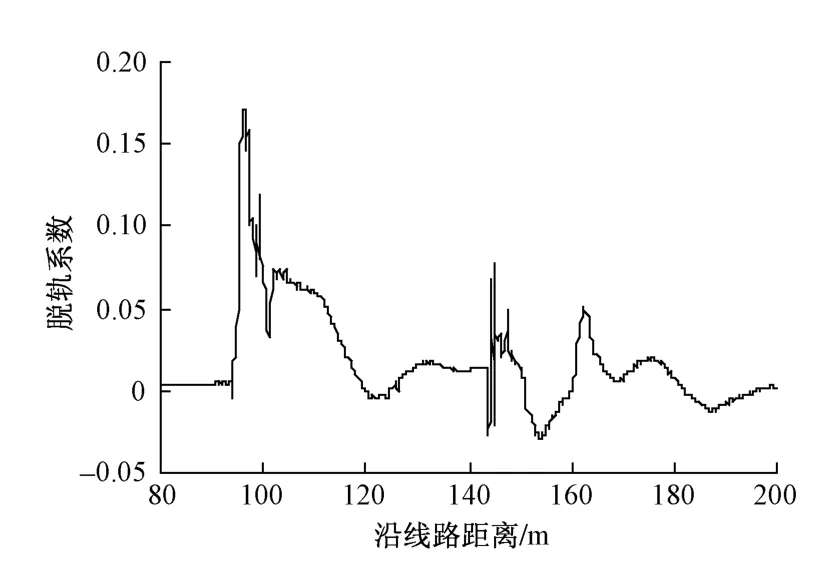
图2 脱轨系数时程曲线

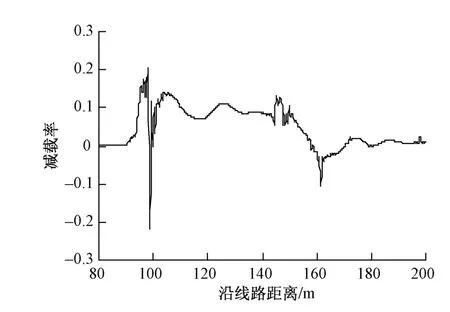
图3 轮重减载率时程曲线

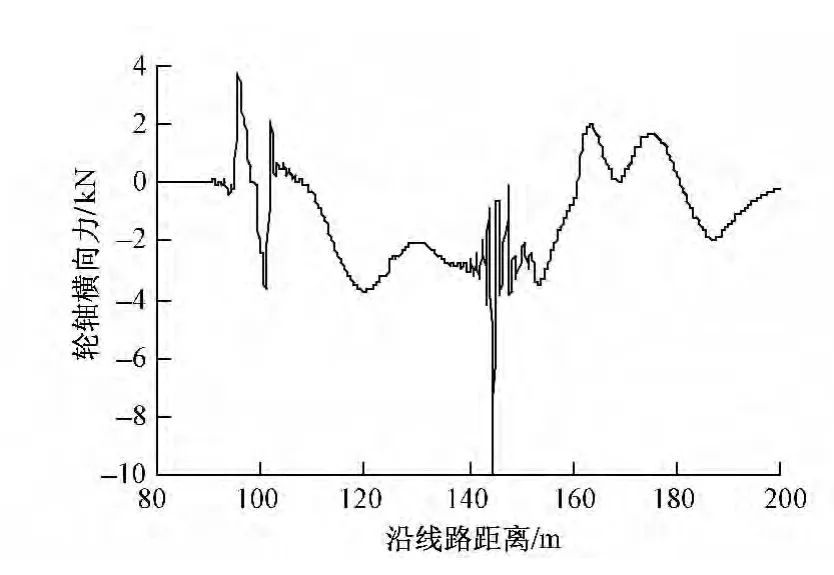
图4 轮轴横向力时程曲线

18号道岔用于线间距分别为4.6，4.8和5.0 m的单渡线时，对应夹直线长度分别为 21.9，25.5，29.1 m，当CRH2以80 km/h侧向通过不同线间距的单渡线时，各项动力响应比较如图5～图7所示。

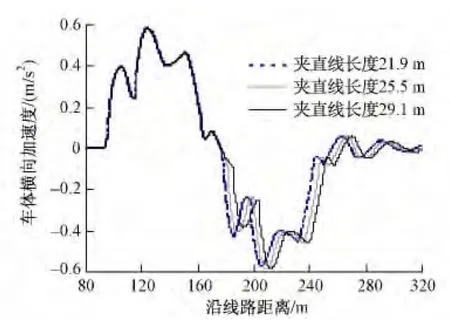
图5 车体横向加速度时程曲线

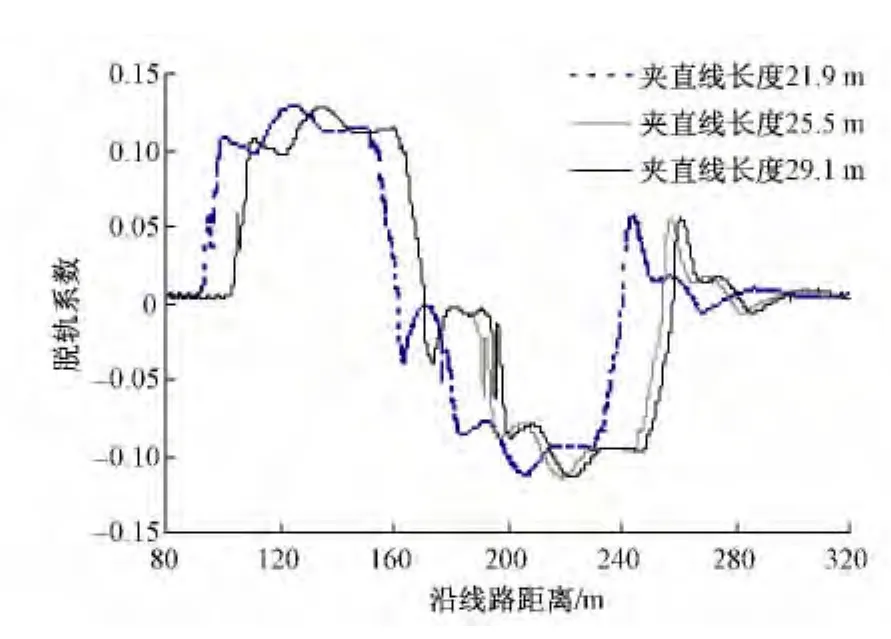
图6 脱轨系数时程曲线

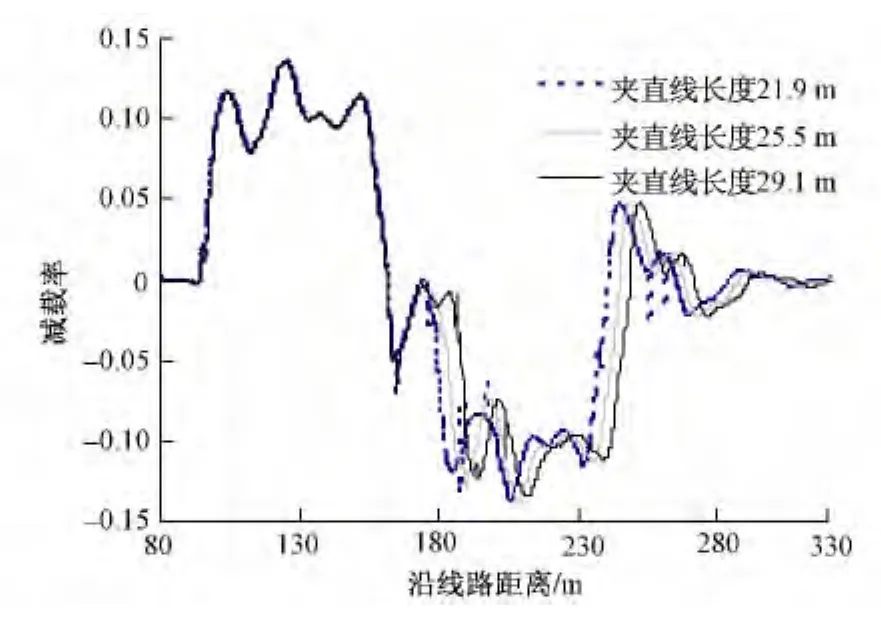
图7 减载率时程曲线

由计算结果可见，动车组侧向通过线间距分别为4.6 m和4.8 m的渡线时，动力响应指标几乎无差异。线间距为5.0 m时，夹直线区段动力学指标明显优于线间距为4.6 m和4.8 m的渡线，但三种线间距时的动力学指标量值仍小于相关评判指标。说明18号道岔可用于三种线间距的单渡线，且规定夹直线长度＞20 m是合理的。

4 42号道岔侧线线型与夹直线长度设计及其仿真计算

4.1 42号道岔侧线线型设计及其仿真计算

42号道岔主要平面参数见表3。

表3 42号道岔主要平面尺寸

利用建立的动车组—道岔动力学仿真模型，对高速铁路42号道岔的动力响应进行仿真计算。当动车组CRH2-300以160 km/h侧逆向通过42号道岔时，车体横向加速度、脱轨系数、轮重减载率、轮轴横向力动力响应时程曲线如图8～图11所示。

从车辆运行舒适性来看，车体垂向、横向振动加速度最大值分别为0.25，0.57 m/s2，＜1.0 m/s2的限值要求;从车辆运行安全性来看，脱轨系数、轮重减载率最大值分别为0.10，0.23，均＜0.8的限值要求。

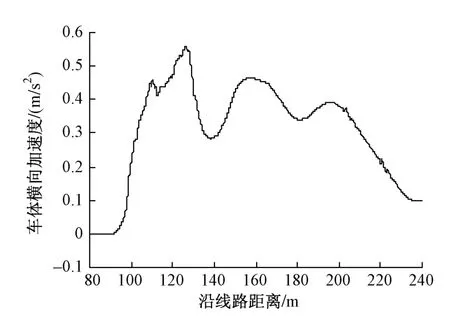
图8 车体横向加速度时程曲线

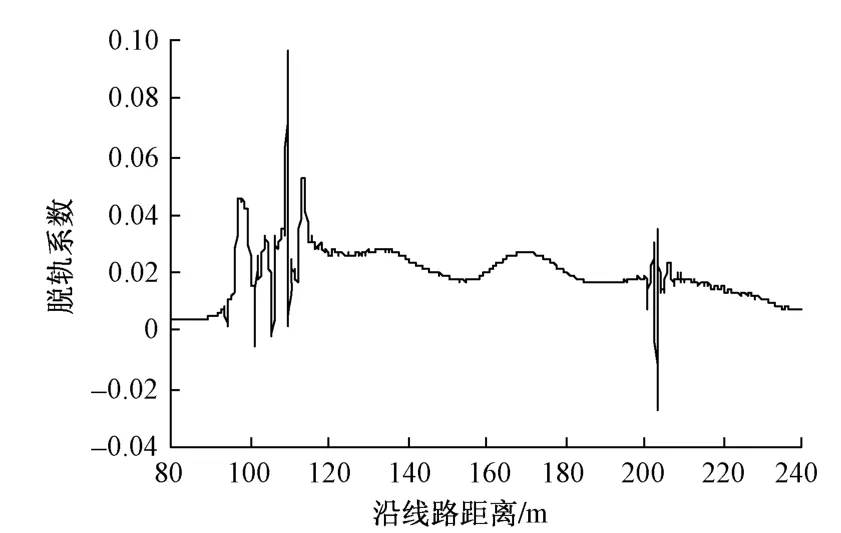
图9 脱轨系数时程曲线

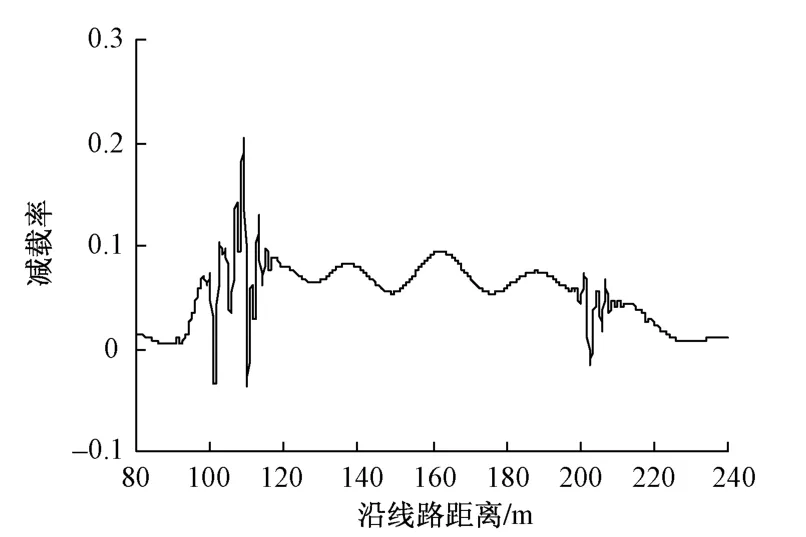
图10 轮重减载率时程曲线

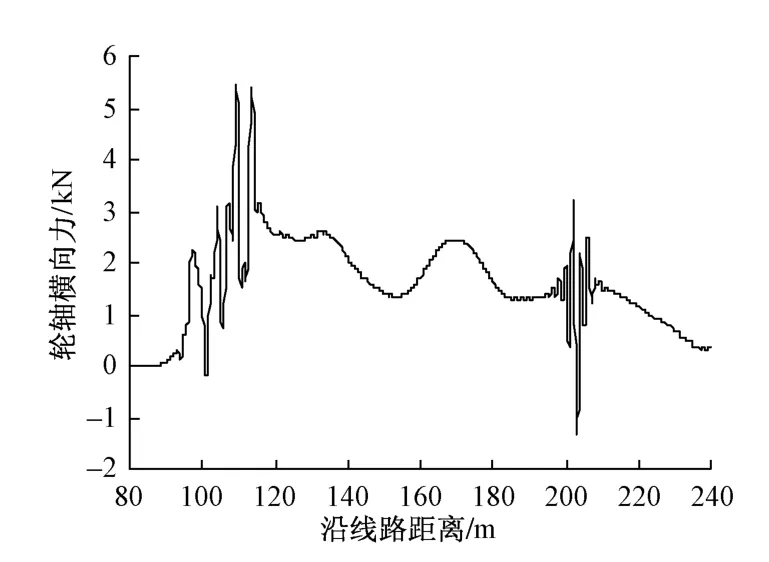
图11 轮轴横向力时程曲线

4.2 42号道岔夹直线长度及其仿真计算

42号道岔用于线间距分别为4.6，4.8，5.0 m的单渡线时，对应夹直线长度分别为0，8.8，17.6 m，当CRH2以160 km/h侧向通过不同线间距的渡线时，各项动力响应比较如图12～图14所示。由计算结果可以看出，当线间距改变时，不同长度的夹直线对各项动力学指标几乎没有影响，说明42号道岔用于单渡线时，两支反向缓和曲线起点间可直接连接或插入任意长度直线段。

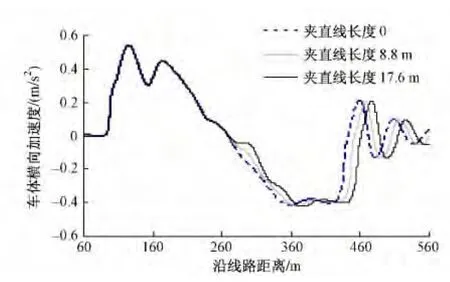
图12 车体横向加速度时程曲线

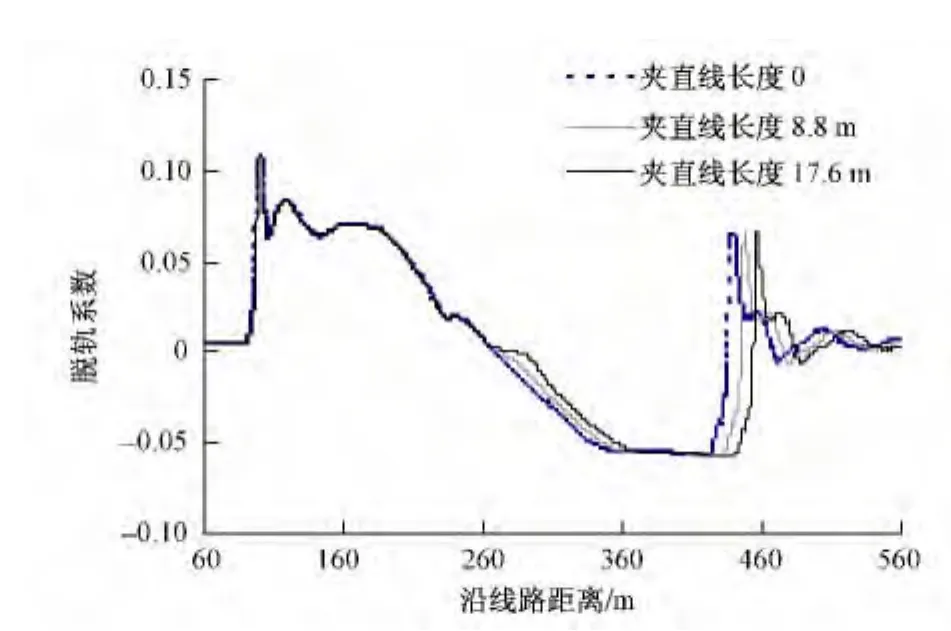
图13 脱轨系数时程曲线

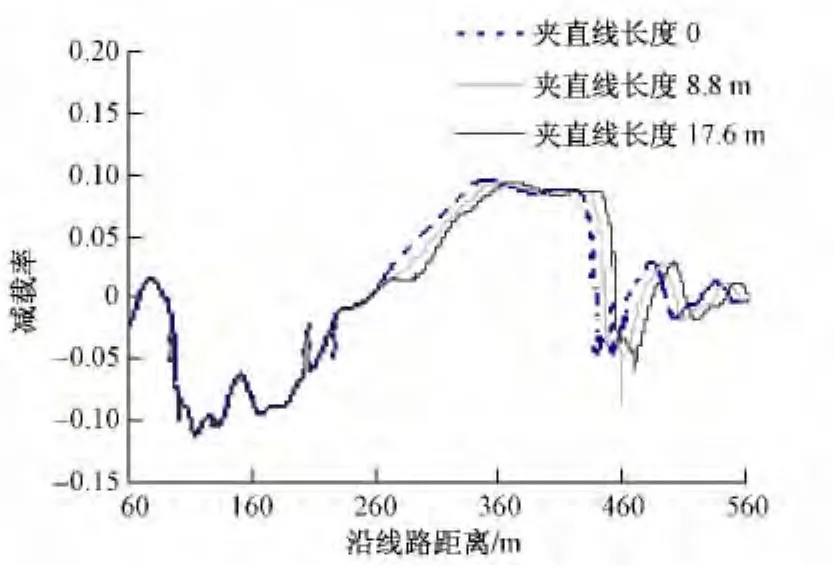
图14 减载率时程曲线

5 结论与建议

1)当动车组以80 km/h和160 km/h侧逆向分别通过18号和42号道岔，道岔动力学指标的理论计算值小于相应限值，表明高速铁路平面设计参数与动力学评价指标的选取及18号和42号道岔的线型设计是正确、合理的。

2)动车组侧向通过线间距分别为4.6，4.8和5.0 m的18号道岔组成的单渡线时，动力响应指标小于相应限值。说明18号道岔可用于三种线间距的单渡线，且要求夹直线长度＞20 m是合理的。

3)42号道岔用于线间距分别为4.6，4.8和5.0 m的单渡线时，不同长度的夹直线对其各项动力学指标几乎没有影响，说明42号道岔用于单渡线时，两支反向缓和曲线起点间可以直接连接或插入任意长度的直线段。

［1］史玉杰.秦沈客运专线道岔平面设计参数的研究［J］.铁道学报，2001，23(4)：94-97.

［2］孙家林，姜卫利.秦沈客运专线大号码道岔线型的分析［J］.铁道建筑，2004(5)：51-52.

［3］孙加林，宣言，王树国.铁路大号码道岔合理线型设置的仿真研究［J］.铁道建筑，2010，50(8)：125-127.

［4］王树国，顾培雄.客运专线道岔技术研究［J］.中国铁路，2007(8)：21-28.

［5］郭福安.国外高速铁路的道岔设计［J］.中国铁路，2006(2)：48-50.

［6］王树国，肖俊恒，顾培雄.客运专线道岔平面线型的研究［R］.北京：铁道科学研究院，2006.

［7］中华人民共和国铁道部.TB/T 3301—2013 高速铁路道岔技术条件［S］.北京：中国铁道出版社，2013.

U213.6

A

10.3969/j.issn.1003-1995.2014.01.26

1003-1995(2014)01-0091-04

2013-10-05;

2013-11-25

王树国(1974— )，男，山东冠县人，副研究员，博士。

(责任审编 王 红)