基于内聚力模型的铝/丁羟胶粘接界面力学研究①

韦 震，鞠玉涛，周清春，韩 波

(南京理工大学机械工程学院，南京 210094)

0 引言

HTPB复合推进剂是一种具有高固体颗粒填充比的高能复合材料，即以丁羟胶为基体和粘合剂，在其中添加铝、AP和黑索金等颗粒。其宏观力学性能主要由粘合剂的粘弹性质、固体颗粒的体积分数和粘合剂基体/颗粒间的界面粘接状况所控制。从界面处开裂脱粘是含界面材料的主要失效方式。因此，研究粘合剂基体(丁羟胶)/颗粒(铝)间的界面粘接状况，对研究复合推进剂的整体力学性能具有重要意义。

随着粘接界面的广泛研究，内聚力模型得到了快速发展。内聚力模型最早是由Dugdale和Barenblatt提出的，Dugdale通过裂缝推进区的概念研究材料的塑性，Barenblatt早期提出CZM用在研究脆性材料的断裂上。Needleman最早为了研究金属材料的颗粒分离现象，提出了多项式和指数型的内聚力-位移法则。Tvergaard和Hutchinson使用梯形内聚力-位移方程，研究了弹塑性材料的裂纹扩展。Espinosa和Zavattieri为了解决多项式和指数型内聚力模型的中的屈服问题提出了双线性模型。由于双线性模型在结构上较简单，但能够很好地表征内聚区的断裂行为，所以得到了广泛应用[1]。

当前在复合推进剂领域，人们关于基体与颗粒的细观力学以及界面脱粘等方面已经做了一些研究。刘著卿等[2]对复合推进剂单轴拉伸试验进行了原位电镜扫描，并通过内聚力模型对基体与颗粒的脱粘与损伤进行了数值仿真。Karel Matous等[3－4]基于有限变形和内聚力模型，对复合推进剂的颗粒脱粘以及界面损伤演化进行了有限元分析。但目前在这方面的有限元计算中，采用的材料的内聚力模型的参数都是通过经验确定或是直接给出，并没有明确的获得过程和依据。目前，也尚未看到有关铝/丁羟胶粘接界面的研究，而铝作为HTPB复合推进剂中的主要固体添加材料，其颗粒与基体的界面粘接也是推进剂力学特性重要的一部分。因此，需要了解铝颗粒在基体中的粘接特性。然而，由于在复合推进剂中，铝颗粒的尺寸非常小，约在几十微米到一百微米之间，现在的细观力学实验水平较难直接对推进剂颗粒的力学状态进行测量。因此，需要进行宏观的双悬臂梁粘接试验。文献[5]指出，复合推进剂中的Al颗粒尺度在丝米量级，可运用连续介质力学和宏观断裂力学方法进行研究，而且颗粒与胶体之间的粘接与双悬臂梁之间的粘接在粘接机理上具有一定的相同之处。例如，湿润与粘附过程，化学反应过程，互扩散与机械作用等。因此，基于宏观试验方法对Al颗粒与HTPB粘接界面的研究，从粘接机理方面是可行的。Jung Gyoo-Dong等[6－7]采用宏观的胶体与AP平板之间的粘接剥离试验获取粘接断裂能，并将宏观获得的断裂能直接用于细观损伤本构模型中，获得了与试验非常吻合的仿真结果，也进一步说明了颗粒与胶体粘接研究宏观化的合理性。

本文通过铝/丁羟胶粘接的双悬臂梁实验，研究了铝/丁羟胶粘接界面的宏观力学性能，基于双线性内聚力模型，进行了数值仿真模拟，并获取了粘接界面的主要界面参数，为进一步细观的研究作为理论基础，最后通过单轴拉伸实验，对所建立的内聚力模型进行了验证。

1 试验方法及结果

使用纯铝板材，粘接剂选用工业用丁羟胶。根据美国ASTM D3433标准[8]，设计了双悬臂梁粘接试件，并通过丁羟胶粘接固化。试件几何形状和尺寸见图1。

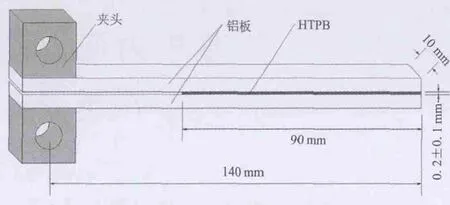
图1 双悬臂梁粘接试件及相关尺寸Fig.1 Geometry and dimensions for the DCB specimens

由于被粘表面的处理是影响粘接质量的重要因素，因此在粘接前，被粘接件的粘接表面要经过脱脂除油、机械处理、化学处理、洗涤和干燥，以除去试件表面的油垢和可能有的杂物。粘接剂在制备完成后，均匀涂抹于被粘表面，在粘接表面夹持一端的前缘预先插入涂有硅胶薄膜的Telfon薄膜，以生成未粘接表面作为初始裂纹。粘接件确保粘接层厚度为(0.2±0.1)mm，有利于粘接表面达到更好的粘接效果，试件制备过程如图2所示。

图2 试件制备图Fig.2 Preparation of specimens

将固化完成的试件标号，并沿初始裂纹向后在双悬臂梁的侧面粘贴光栅，便于图像数据的采集和后期处理分析。

将加工完成的双悬臂梁试件与单轴拉伸试验机上下铰接，在连接时确保上下夹头的同轴度，并使双悬臂梁加载块的孔与连接销之间为间隙配合，保证悬臂梁可在竖直平面内自由转动，并通过显微镜CCD对试验过程进行实时图像采集，如图3所示，拉伸速率为1 mm/min。

在25℃、相对湿度44%环境下，完成双悬臂梁试件的单轴拉伸试验，并获得加载点载荷-位移曲线，如图4所示。图4中，有图标的曲线为试验实际获得的曲线，粗实线为试验曲线的平均曲线。

由于在制备过程中双悬臂梁粘接表面粗糙度、粘接层厚度以及粘接工艺等随机误差的存在，导致试验曲线之间存在一定程度的偏差。从图4可看出，在试验的起始阶段，也就是曲线的上升段的前半部分重合性不是很好，主要是因为初始裂纹长度的细微差别及裂纹尖端形状差异对曲线初始段产生了影响。但从图4中试验曲线的整体趋势、上升段斜率以及重合度来看，试验曲线的趋势是一致的，且不确定度的影响很小，载荷-位移曲线的整体标准差很小。因此，可认为试验数据是可信的。

图3 试件试验图Fig.3 Experiment of specimens

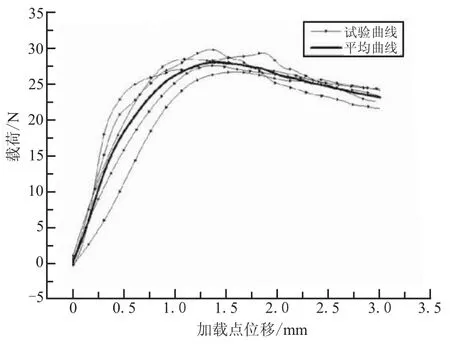
图4 1 mm/m in拉伸速率下双悬臂梁的载荷-位移试验曲线及平均曲线Fig.4 Experimental load-displacement curves and average curve for DCB tests at v=1mm/m in

2 Ⅰ型断裂内聚力模型参数获取方法

2.1 分部反演识别方法

本文主要研究铝板与丁羟胶在I型断裂下的内聚力模型。由于数值仿真结果已经说明内聚力-张开位移法则的精确形状不会从根本上影响分析的结果[9]。因此，这里选择了最为常用双线性模型。双线性CZM的t-δ(内聚力-位移)曲线如图5所示。其中，t为内聚力;δ为裂缝面的相对位移;Tc为内聚力所能达到的最大值，称为断裂强度;δ0为达到断裂强度时裂缝面的位移;δf为裂缝面的最大位移，称为失效位移;GIc为裂缝面从开裂到失效所消耗的能量，称为断裂能。在内聚力达到断裂强度前(δ≤δ0)，内聚力区域的材料是线弹性的，内聚力随着张开位移线性增长;在内聚力达到断裂强度之后(δ≥δ0)，材料表现为线性软化行为。当δ0＞δ＞δf时，是材料的软化阶段，也称为损伤阶段。

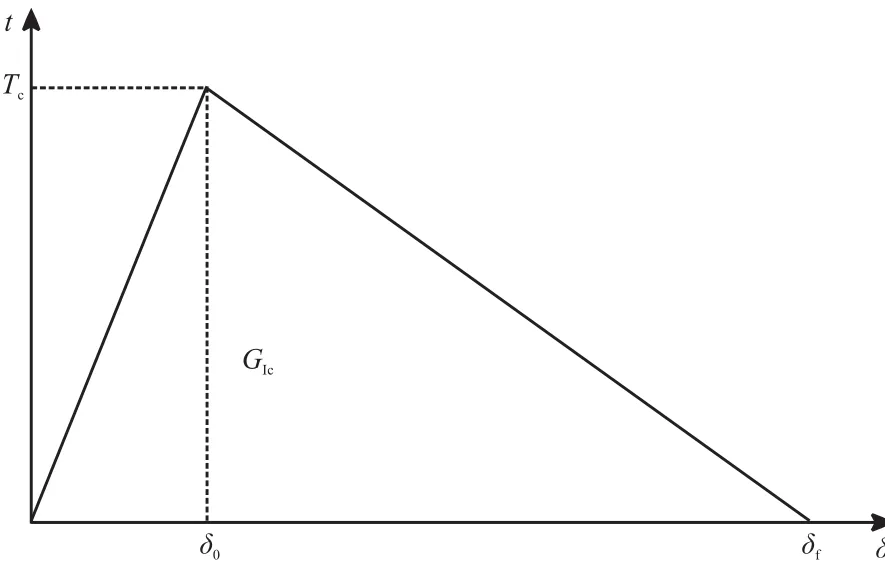
图5 双线性内聚力模型的内聚力-张开位移曲线Fig.5 Traction-separation law of bilinear cohesive zonemodel

在这个模型中，需要确定2个独立的参数，即断裂能GIc和断裂强度Tc。本文将通过仿真曲线与试验曲线匹配的分部反演方法获得内聚参数。这里首先将试验曲线表示为一定数量点的集合，即

然后，通过ABAQUS仿真曲线可同样得到n个x坐标相对应点的集合，即

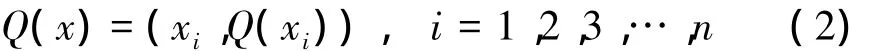
为了使仿真曲线与试验曲线尽可能的重合，得到更加准确的内聚参数，可通过在一定范围内搜索断裂能和断裂强度的值来满足以下目标函数:

其中，R为试验曲线与仿真曲线对应的均方误差，R的大小可很好地反映试验曲线与仿真曲线的重合程度，当R为最小时，表示仿真曲线与试验曲线重合度最好，此时得到的内聚参数为最符合实际情况的，反演流程如图6所示。

在数值仿真初步的参数调试过程中，发现了本模型的一个特点:裂纹长度和断裂强度不影响载荷位移曲线峰值之后的下降部分(衰减段)，而断裂能对载荷位移曲线的上升段斜率不产生影响。这个特点与文献[10]中的结论相同。图7为分别只改变断裂强度或断裂能获得的仿真载荷位移曲线。由图7可看出，断裂强度只影响上升段的斜率和峰值载荷，当断裂强度越大时，载荷位移曲线的斜率越大，峰值也越大;而只有断裂能决定着曲线的下降部分(衰减段)。

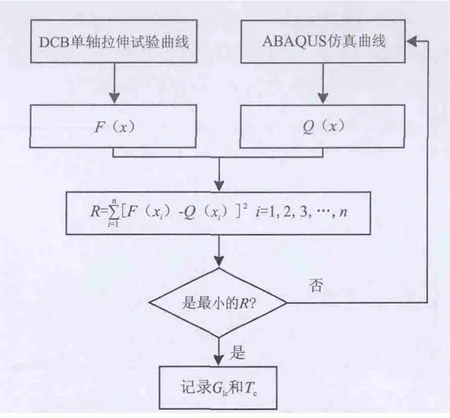
图6 内聚参数反演流程图Fig.6 Flow chart of the inverse procedure

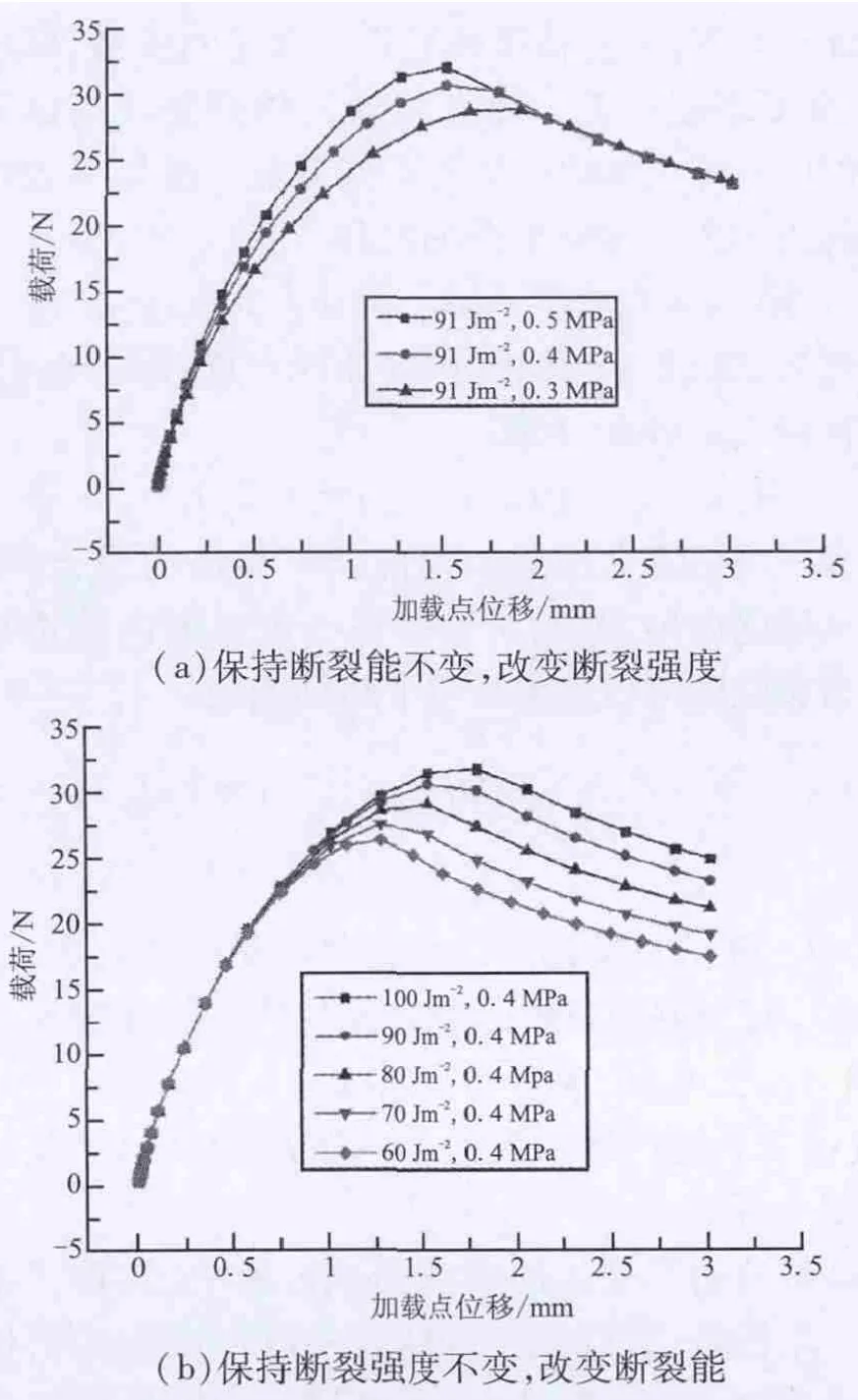
图7 仿真曲线Fig.7 Simulation curves

为提高工作效率，结合以上特点，可将上述反演过程分为2部分:首先，通过试验曲线和仿真曲线的衰减部分(即F'(x)≤0)的匹配，可确定断裂能的数值大小。当断裂能确定之后，即双线性内聚力模型曲线下的面积确定了。然后，需要通过对整个内聚区的分析来确定断裂强度。在整个内聚区的分析中，初始裂纹长度起到重要作用。因此，在本次试验中，统一裂纹初始长度为50 mm。通过上述确定的断裂能和在一定范围内搜索断裂强度，使试验曲线与仿真曲线的上升段和载荷峰值(即F'(x)≥0)很好的匹配，这时就得到了另一个内聚参数——断裂强度。

一般的反演方法是对2个参数的最优化求解过程，需要用到较复杂的优化算法，而这里利用双线性模型2个参数分别只对载荷-位移曲线的上升段和衰减段有影响的特点，通过分部反演的方法大大简化了反演过程，每一步只需要确定一个变量，使这种方法更加具有可操作性。

2.2 断裂力学方法

上述内容介绍了使用双线性内聚力模型数值仿真与试验对比的分部反演识别方法获取内聚力模型的2个主要参数。但由于需要在仿真过程中大范围搜索，以获取合理的内聚参数，因此造成工作量很大，比较费时。这里将探讨获取以上参数的断裂力学方法。

在线弹性断裂力学中，以柔度法表示的能量释放率的表达式为

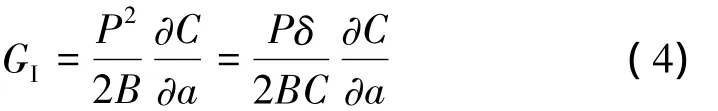
式中P为外加载荷;B为悬臂梁的宽度;C为试件的柔度;a为裂纹长度;δ为加载点的位移。

当裂纹扩展所需的能量恰好等于所获外界能量时，裂纹面处于临界状态，此时的能量释放率即为弹性体的断裂韧性。根据上式，并用Pc表示试验起裂载荷以及对应的加载点位移δc，此时求得的临界能量释放率为试件的断裂韧性，其表达式为[11]

根据经典梁理论，试件的加载点位移δ也就是梁的扰度可表示为

因此，可得到经典梁理论下的断裂韧性为

通过经典梁理论，可较方便地获取I型断裂粘接界面的断裂韧性。

3 内聚力模型参数获取结果分析及验证

3.1 内聚力模型参数获取结果

采用ABAQUS有限元商业软件进行数值仿真，使用双线性CZM模拟铝板与HTPB的DCB试验。建立三维DCB模型，如图8所示。

整个粘接层为布置4节点的COH3D8单元，初始厚度为 0.1 mm。被粘接件建模为弹性模量E=70 GPa，泊松比为0.33的均质弹性体，采用 C3D8I单元。建模尺寸以及初始裂纹长度与试验试件相同。通过上述分部反演方法获得的铝/丁羟胶粘接件I型断裂的内聚参数分别为断裂能GIc=(83±8)J/m2和断裂强度Tc=(0.35±0.05)MPa。图 9 所示为通过 DCB 试验获得的断裂能与断裂强度作为仿真参数得到的预测曲线与DCB试验得到的载荷-位移曲线的对比。其中，两根粗实线为反演获得的内聚参数范围的仿真曲线，带图标曲线为试验的平均曲线及对应点的标准差。

图8 ABAQUS双悬臂梁仿真建模与结果Fig.8 Numerical simulation results of DCB

图9 双悬臂梁载荷-位移曲线的对比Fig.9 Comparison of DCB load-displacement curves

同时，通过上述断裂力学方法，将前述DCB试验的数据代入上述经典梁理论下的断裂韧性公式(7)，并取Pc为载荷-位移曲线中的峰值载荷，δc为对应的加载点位移，同样可获取试验界面的断裂能，结果如表1所示。

将经典梁理论获得的断裂能，以及反演获得的平均断裂强度作为内聚参数进行数值仿真，结果如图9中虚线所示。从图9可看出，采用分部反演识别方法获取的内聚参数的仿真曲线，可很好地与试验曲线重合，然而通过经典梁理论获取参数的仿真结果的峰值载荷和后半段明显过高。因此可说明，通过分部反演识别方法获取的内聚参数更为准确，基本可反映粘接界面的真实性质。

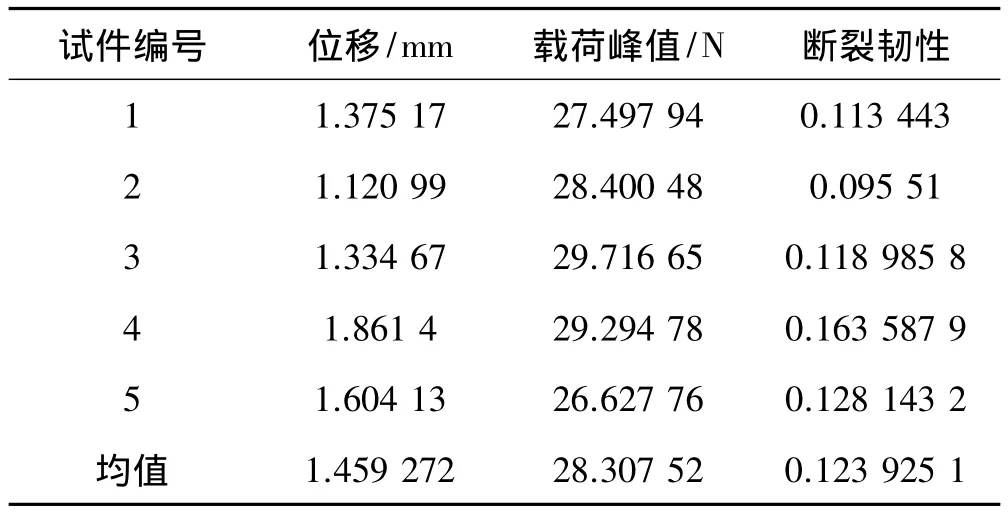
表1 通过经典梁理论得到的试验中双悬臂梁粘接件的断裂韧性及平均值Table 1 Fracture toughness obtained by the classical beam theory and average value

从表1可看出，使用经典梁理论方法得到的断裂韧性的数值的平均值为123.93 J/m2，明显大于分部反演得到的断裂能的值83 J/m2，分析原因主要有:

(1)在计算梁扰动时，式(7)是在理想的悬臂梁情况下得到的，没有考虑剪切的影响。文献[12]在计算梁扰度时，考虑了剪切的影响，得到加载点位移的公式:

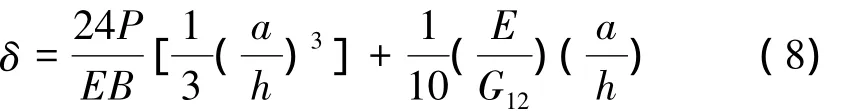
其中，G12为剪切模量。式中第2项为梁在弯曲过程中由于剪切变形效应引起的，由于本试验中梁为各向同性的铝板，E/G12的值为2.66，因此第2项对薄试件的影响不显著，而且当a/h≥10时，剪切效应减小到2.9%以下[13]，基本可认为对试验不产生影响，这也正是本试验中初始裂纹选择50 mm的原因。

(2)式(7)是在理想情况下，并且是在线弹性断裂力学基础上得到的，没有考虑到大变形，裂尖转动等方面的影响[14]，而且由图4可看出，在上升段临近峰值载荷的最后一部分已经出现了非线性。因此，这些也会对式(7)的结果产生影响。

(3)在表1所得到的结果中，Pc选用的是载荷-位移曲线中的峰值载荷。有些研究认为，DCB的载荷-位移曲线的峰值载荷就是粘接层的开裂载荷，但有些研究则认为，开裂点在峰值载荷点之前一小段，而Pc应选用开裂点载荷，这也是造成式(7)结算结果与仿真得到的参数之间差距的一个原因。

综上可看出，虽然采用线弹性断裂力学基础以及经典梁理论获得的断裂韧性的值与实际材料的I型断裂能的值有一定差距，但可作为仿真时调整参数的参考值来使用，使仿真中调整断裂能的参数时有一定依据，可大大减少工作量。

3.2 内聚力模型及参数验证

上文中已经得到了Al/HTPB粘接件I型断裂的内聚力模型及相关参数——断裂强度和断裂能的值。这里将通过另外一种形式的粘接件——单轴拉伸试件对上文得到的内聚力模型及参数进行验证。

单轴拉伸实验参照美国行业标准ASTM中关于粘接试件拉伸断裂的标准ASTM D2095[15]完成。

单轴拉伸被粘接件采用与DCB梁相同的铝材料加工而成，尺寸为70mm×25mm×10mm。在试件一端靠近端面处加工直径为8 mm的通孔作为夹持孔，便于试验时夹持，如图10所示。

图10 单轴拉伸试件与ABAQUS模型Fig.10 Uniaxial tensile specimen and ABAQUSmodel

通过HTPB将被粘接件中间表面粘接在一起，形成一定厚度为(0.2±0.1)mm的粘接层。拉伸试件与DCB试件一批制备完成，这样可使拉伸试件制备方法及HTPB的固化工艺与DCB试件的基本相同，更好地保持粘接界面性质相同。拉伸试验也与前文的DCB试件的拉伸试验相同，采用1mm/min的加载速率在万能试验机上完成，并得到粘接件的粘接强度。

ABAQUS仿真中，完全按照单轴拉伸试验建立模型，粘接层单元使用内聚力单元，并使用前文中获得的HTPB内聚力模型及2个相关参数，断裂强度选用均值0.35 MPa，断裂能选用均值83 J/m2，仿真结果与试验结果见表2。

表2 单轴拉伸试验断裂强度与仿真结果对比Table 2 Com parison of fracture strength of uniaxial tensile test and numerical simulation results

从表2可看出，使用平均参数进行的仿真结果位于试验结果范围内，说明前文通过DCB试验得到的内聚力模型及相关参数能够很好预测单轴拉伸试验的粘接强度，也证明本文建立的Al/HTPB的I型断裂的内聚力模型及得到的相关参数是正确的，能准确反映材料的粘接特性。

4 结论

(1)将双悬臂梁试验用于Al和HTPB粘接界面的I型断裂研究，获得了粘接界面裂纹的稳定扩展过程，并得到了Al/HTPB粘接试件的载荷-位移曲线。

(2)基于双线性内聚力模型，在ABAQUS中建立了粘接试件的三维仿真模型，并通过所建立的分部反演的数值方法获取了内聚力模型的2个参数——断裂能为GIc=(83±8)J/m2和断裂强度为Tc=(0.35±0.05)MPa。

(3)比较了通过断裂力学方法和数值仿真方法分别获得的断裂能的值，结果表明，粘接件的断裂韧性在数值上与得到的断裂能有一定差距，但可在一定程度上作为获得断裂能参数的依据，具有参考价值，而通过仿真曲线与试验曲线相匹配的方法得到的内聚参数更加真实，更能反映材料的真实性能。

(4)通过Al/HTPB粘接的单拉伸试件，对获得的内聚参数进行了验证，证明了所使用的双线性内聚力模型的适用性及所得到的内聚参数的正确性，为进一步研究HTPB推进剂的细观力学行为，得到了宏观界面参数和模型依据。

[1] 张东.基于内聚力模型的沥青路面断裂研究[D].南京:东南大学，2010.

[2] 刘著卿，李高春，邢耀国，等.复合固体推进剂细观损伤扫描电镜实验及数值模拟[J].推进技术，2011，32(3):412-416.

[3] Karel Matous，Philippe H Geubelle.Finite element formulation formodeling particle debonding in reinforced elastomers subjected to finite deformations[J].Computer Methods in Applied Mechanics and Engineering，2006，196:620-633.

[4] Karel Matous，Philippe H Geubelle.Multiscale modelling of particle debonding in reinforced elastomers subjected to finite deformations[J].Int.J.Numer.Meth.Engng.，2006，65:190-223.

[5] 杨卫.宏微观断裂力学[M].北京:国防工业出版社，1995:6-7.

[6] Jung Gyoo-Dong，Youn Sung-Kie.A nonlinear viscoelastic constitutivemodel of solid propellant[J].International Journal of Solids and Structures，1999，36:3755-3777.

[7] Jung Gyoo-Dong，Youn Sung-Kie，Kim Bong-Kyu.A three-dimensional nonlinear viscoelastic constitutive model of solid propellant[J].International Journal of Solids and Structures，2000，37:4715-4732.

[8] Philadelphia，PA.ASTM D3433-Standard test method for fracture strength in cleavage of adhesives in bonded metal joints[S].USA:American Society for Testing and Material，1999(Reapproved 2005)

[9] Li S，Thouless M D，Waas A M，et al.Use of a cohesive-zone models to analyze the fracture of a fiber-rein forced polymermatrix composite[J].Composite Science and Technology，2005，65:537-549.

[10] Li S，Thouless M D，Waas A M，et al.Use of mode-I cohesive-zonemodels to describe the fracture of an adhesivelybonded polymer-matrix composite[J].Composite Science and Technology，2005，65:281-293.

[11] 王智宇，王安稳.橡胶-钢粘接界面断裂韧性实验研究[J].固体力学学报，2010，31:204-208.

[12] 矫桂琼，徐家瑶.复合材料I型断裂韧性GIc和初始裂纹长度[J].应用力学学报，1995，12(2):47-55.

[13] 于志成，矫桂琼.复合材料在DCB试验中的裂纹尺寸效应[J].航空材料学报，1996，16(4):46-53.

[14] Albertsen H，Ivens J，Peters P，et al.Interlaminar fracture toughness of CFRP influenced by fiber surface treatment:part 1.experimental results[J].Composite Science and Technology，1995，54:133-145.

[15] Philadelphia，PA.ASTM D2095-Standard Test Method for Tensile Strength of Adhesives by Means of Bar and Rod Specimens[S].USA:American Society for Testing and Material，1996(Reapproved 2002).