空间臂式补偿机构轴承预紧力与系统刚度关系分析

王 智,郭万存

(中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033)

空间臂式补偿机构轴承预紧力与系统刚度关系分析

王 智*,郭万存

(中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033)

为了补偿空间光学望远镜在轨跟踪目标过程中受空间各种因素影响而导致的光学系统视轴和目标之间产生的相对移动和旋转(即指向偏差和指向振荡)，设计由臂式补偿机构控制望远镜补偿与目标的相对运动。但由于臂式补偿机构的尺寸和质量严格限制在一定范围内，且望远镜尺寸很大，质量达3 000 kg，这种结构形式导致系统刚度很低。为了满足控制系统提出的结构高刚度要求，在系统结构形式确定的情况下，分析施加轴承预紧力提高系统刚度的可行性。分析了轴承预紧力、轴承刚度和系统刚度之间的关系，获得了轴承预紧力与系统固有频率的关系。分析证明在系统结构形式确定的情况下，施加合适的轴承预紧力，可以提高系统的刚度，同时为轴承最佳预紧力的确定提供了一个有效的方法。

臂式补偿机构；轴承；预紧力；刚度

1 引言

空间光学望远镜在轨跟踪目标过程中，受轨道运动、姿态变化、控制系统的负载特性、振动等因素的影响，光学系统的视轴和目标之间将不可避免地产生相对移动和旋转(即产生指向偏差和指向振荡)，从而导致成像质量下降。为了补偿这些因素产生的影响，设计由臂式补偿机构控制光学望远镜补偿与目标的相对运动。

受舱内空间以及质量的限制，臂式补偿机构的尺寸及质量严格限制在一定范围内，而空间望远镜的质量达3 000 kg，尺寸巨大，这种结构形式导致系统刚度很低，而跟踪及控制系统精度要求臂式补偿机构的刚度尽可能高。臂式补偿机构主要由X关节、Z关节、Y关节组成，在轨振动、冲击以及低速工作模式，要求所用轴承有较高的轴向、径向刚度；同时，臂式补偿机构的跟踪精度还要求轴承具有较高的定位精度和低的摩擦力矩。在这种情况下，为了提高臂式补偿机构的刚度和精度，补偿机构的关节在设计时采用配对、能预紧的角接触球轴承。

对配对使用的角接触球轴承施加合适的预紧力，可以提高轴承刚度、关节轴系的旋转精度，减小振动噪声，消除轴向游隙。在安装轴承时，如果实际预紧力大于最佳预紧力，虽然可以获得较高的关节轴系刚度及抗卸载能力，但会使轴承摩擦力矩过大，导致温升加剧，降低轴承寿命；如果实际预紧力小于最佳预紧力，虽然摩擦力矩小了，但轴承刚度将不能满足系统刚度的要求，在较大加速度下容易发射卸载，出现间隙。因此，施加预紧力的准确性对于轴承的性能以及系统的性能都有很大的影响［1-4］。

在系统结构形式确定的情况下，分析施加轴承预紧力提高系统刚度的可行性，通过分析轴承预紧力、轴承刚度和系统刚度的关系，获得了轴承预紧力与系统固有频率的关系，同时也为轴承最佳预紧力的确定提供了一个有效的方法。

2 臂式补偿机构结构［5-9］

单个角接触球轴承只能承受一个方向的轴向载荷，在承受径向载荷时，会引起附加轴向力，必须施加相应的反向载荷。因此，角接触球轴承需成对使用，且通过轴向定位预紧提高其刚度。考虑到臂式补偿机构的工作模式及空间力、热环境，各关节轴系轴承的配置均采用一端固定，另一端游动的方式，如图1所示。考虑到空间望远镜在巡天、对地工作模式转换时，臂式定位机构的负载惯量是变化的，因此，为了增加关节轴系的抗弯刚度，臂式补偿机构(见图2)各关节轴系固定端角接触球轴承均采用如图3所示的配对方式，采用轴向定位预紧；关节轴系游动端采用深沟球轴承，其内圈和轴之间可以滑动，以消除温度变化对轴系产生的变形。

图1 轴系轴承配置方式Fig.1 Bearing configuration of shafting

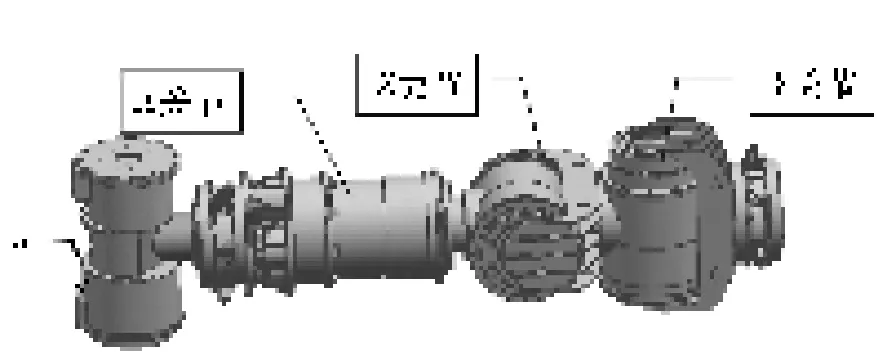
图2 臂式补偿机构模型Fig.2 Model of arm compensation mechanism

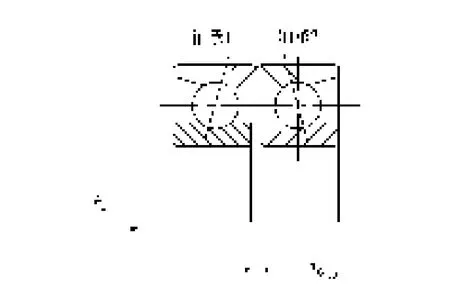
图3 角接触球轴承配对方式Fig.3 Partnership pattern of angle contact ball bearing

3 轴承预紧力与轴系刚度关系计算公式

采用臂式补偿机构控制3 000 kg空间望远镜的这种结构形式，系统刚度很低。为了满足跟踪和控制精度对臂式补偿机构提出的高刚度要求，提出从轴承的配置方式、轴承预紧力方面提高系统的刚度。因为，轴承的预紧力影响着轴承的刚度，轴承的刚度影响着关节轴系的刚度，关节刚度影响着系统的固有频率。所以，通过分析轴承预紧力与轴承刚度、关节轴系刚度的关系，建立轴承预紧力与系统固有频率的关系曲线，确定轴承最佳预紧力。

3.1 轴承预紧力与轴承刚度关系分析

关于臂式补偿机构与空间光学望远镜工作状态时的位置关系(见图6)，其Y、Z关节轴系仅受径向载荷，轴承径向刚度可以用简化计算公式［10］获得：

X关节轴系仅受轴向载荷，轴承轴向刚度可以用简化计算公式获得：

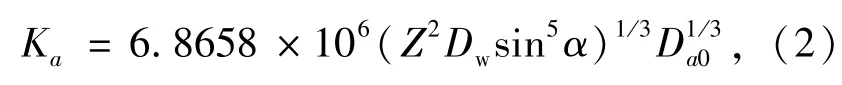
式(1)、(2)中：Dw为钢球直径，Z为单个轴承钢球数目，α为接触角，Fa0为所施加的轴向预紧力。

在设计臂式补偿机构时，需要考虑系统的力学环境适应性(正弦、随机)，要能承受卫星发射过程的振动、冲击。因此动态情况下，需要分析在径向、轴向联合负荷作用下轴承的刚度，采用近似的计算方法，轴承的刚度为［10］：

轴向刚度：

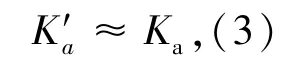
径向刚度：

由轴承动态刚度的近似公式可以看出，联合负荷情况下轴承的径向刚度为纯径向负荷条件下径向刚度的2倍左右，原因是轴向负荷的施加使原本只在径向负荷下近一半钢球承载的情况变成了几乎所有钢球承载，因此轴承径向刚度成倍提高，所以轴向预紧力有利于提高轴承的径向刚度。

3.2 轴承预紧力与关节轴系刚度之间的关系

(1)关节轴系固有频率计算

Y、Z关节轴系固有频率计算［11］：

由前面的分析可以得知，给配对使用的角接触球轴承施加合适的预紧力，可以提高轴承的刚度，进而提高关节轴系的刚度。而关节轴系的刚度可以由其固有频率来表征，静态情况下Y、Z轴系可以简化为如图4所示的弹簧质量系统，该关节轴系的固有频率为：

式中，Wn=f/2π，f为轴系固有频率，m为轴系质量，k1、k2分别为柔性元件1，2的刚度，l1、l2分别为柔性元件1、2相对于振动体中心O的距离，l= l1+l2，I为振动体的转动惯量。

由式(5)可以看出，Y、Z关节轴系的固有频率取决于系统的质量、刚度及轴承的分布，在图4所示的系统中，轴系的质量、转动惯量及轴承的分布可以很容易计算出，所以Y、Z关节轴系的固有频率就取决于轴承的刚度，即轴向定位预紧角接触球轴承的刚度。

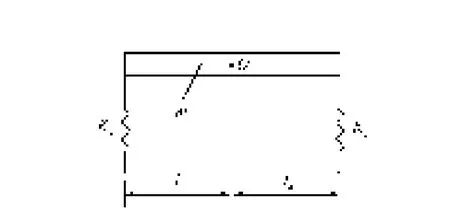
图4 弹簧质量系统Fig.4 System of spring-mass

X关节轴系固有频率计算［12］：

X关节仅受轴向载荷，X关节轴系的轴向振动模型如图5所示，可以得到X关节轴系轴向刚度与固有频率的关系：

式中，ωn=f/2π，f为X关节轴系固有频率，m为轴系质量。

由式(6)可以看出，X关节轴系的固有频率取决于定位预紧角接触球轴承的刚度。

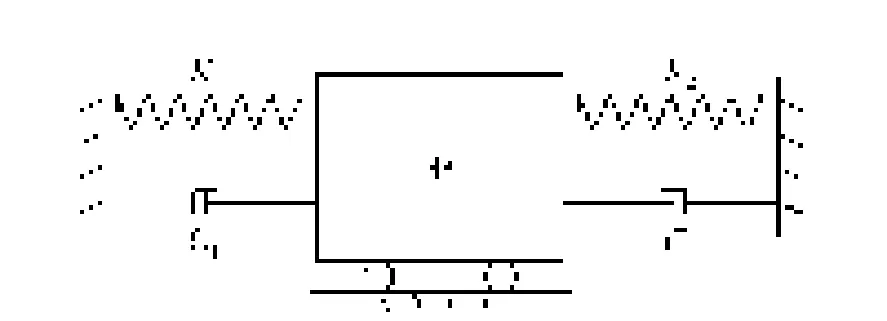
图5 轴系轴向振动模型Fig.5 Axial dynamic model of a shafting

(2)轴承预紧力与轴系刚度的关系公式

Y、Z关节轴系：

臂式补偿机构Y、Z关节轴系所用角接触球轴承为71828C，由式(1)可知，轴向定位预紧角接触球轴承的径向刚度与所施加的预紧力有关；由式(5)可知，轴系的刚度与轴系的质量、角接触球轴承的刚度及分布有关。综合式(1)、(5)可以得到轴承预紧力与轴系固有频率的关系：

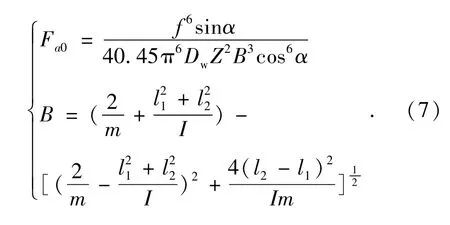
X关节轴系：

臂式补偿机构X关节轴系所用角接触球轴承为71828C，轴承预紧力与轴系固有频率的关系为：

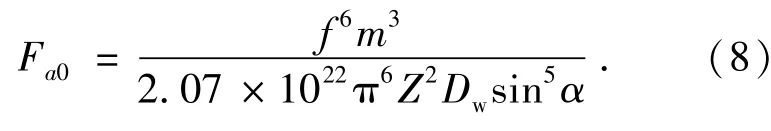
由式(7)、(8)可以看出，在轴系结构已定的情况下，轴承的预紧力与轴系的固有频率有关。

4 轴承预紧力与系统基频的关系曲线

4.1 轴承预紧力与系统基频的关系分析

臂式补偿机构与空间望远镜的有限元模型如图6所示。

图6 系统有限元模型Fig.6 Finite element model of system

(1)X关节轴承预紧力对系统基频的影响分析

在图6所示的系统有限元模型中，对X关节角接触球轴承施加预紧力，Z、Y关节角接触球轴承不施加预紧力。臂式补偿机构与空间望远镜系统的一阶模态频率与X关节的角接触球轴承预紧力关系如表1所示。

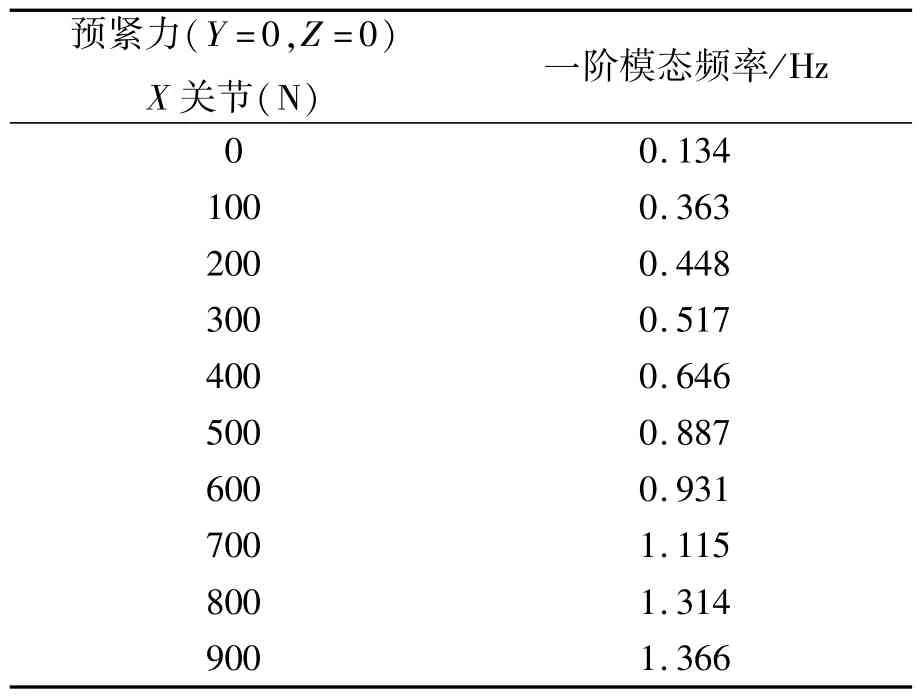
表1 系统一阶模态频率与X关节轴承预紧力关系Tab.1 Relationship between preload of X-joint bearing and first modal frequency of system

(2)Z关节轴承预紧力对系统基频的影响分析

对Z关节角接触球轴承施加预紧力，X、Y关节角接触球轴承不施加预紧力。此时，臂式补偿机构与空间望远镜系统的一阶模态频率与Z关节角接触球轴承预紧力关系如表2所示。

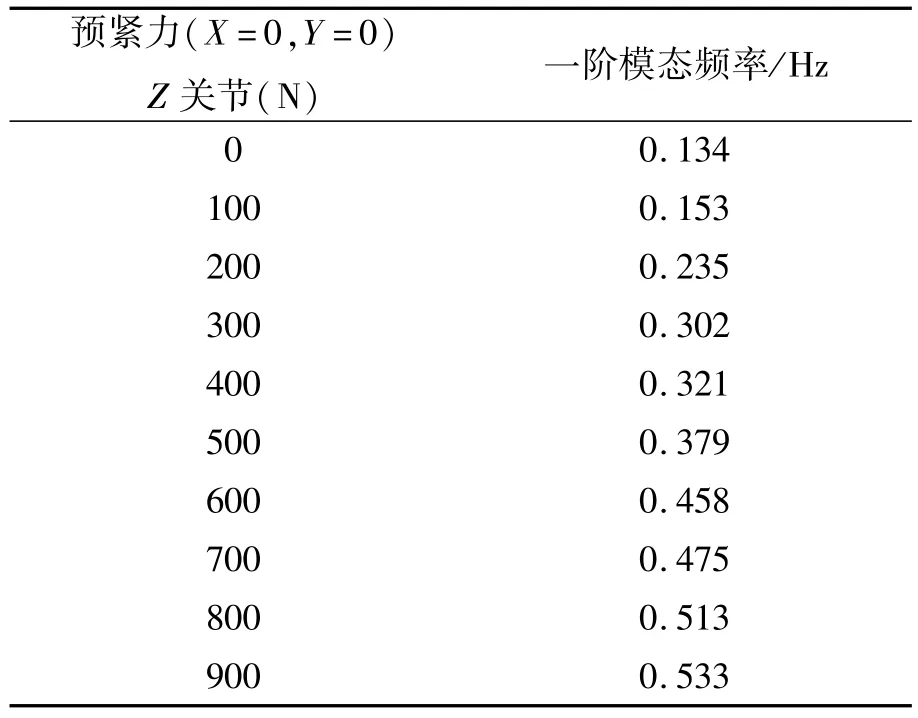
表2 系统一阶模态频率与Z关节轴承预紧力关系Tab.2 Relationship between preload of Z-joint bearing and first modal frequency of system

(3)Y关节轴承预紧力对系统基频的影响分析

对Y关节角接触球轴承施加预紧力，Z、Y关节角接触球轴承不施加预紧力。此时，臂式补偿机构与空间望远镜系统的一阶模态频率与Y关节的角接触球轴承预紧力关系如表3所示。

表3 系统一阶模态频率与Y关节轴承预紧力关系Tab.3 Relationship between preload of Y-joint bearing and first modal frequency of system

从以上分析结果中可以得出，X关节的角接触球轴承预紧力对臂式补偿机构与空间望远镜系统的一阶模态频率影响最大，Y关节的角接触球轴承预紧力对系统的一阶模态频率影响最小。因此，为了提高臂式补偿机构与空间望远镜系统的动态刚度，应首先确定X关节轴承的预紧力。

4.2 最佳预紧力的确定

臂式补偿机构的最高补偿角速度为0.5°/s，不考虑轴承温升的影响，所以确定臂式补偿机构关节轴承的预紧力时仅需考虑臂式补偿机构与空间望远镜系统的动态刚度、关节启动力矩、发射和回扫过程中的卸载力等因素的影响。

X关节轴承预紧力对系统动态刚度的贡献最大，因此，系统的动态刚度应主要由X关节轴承预紧力进行保证。跟踪和控制系统要求系统的一阶模态频率高于1 Hz，所以X关节的轴承预紧力初步确定为700 N，此时，如果Y关节轴承不预紧，系统动态刚度随Z关节轴承预紧力的关节见表4所示。

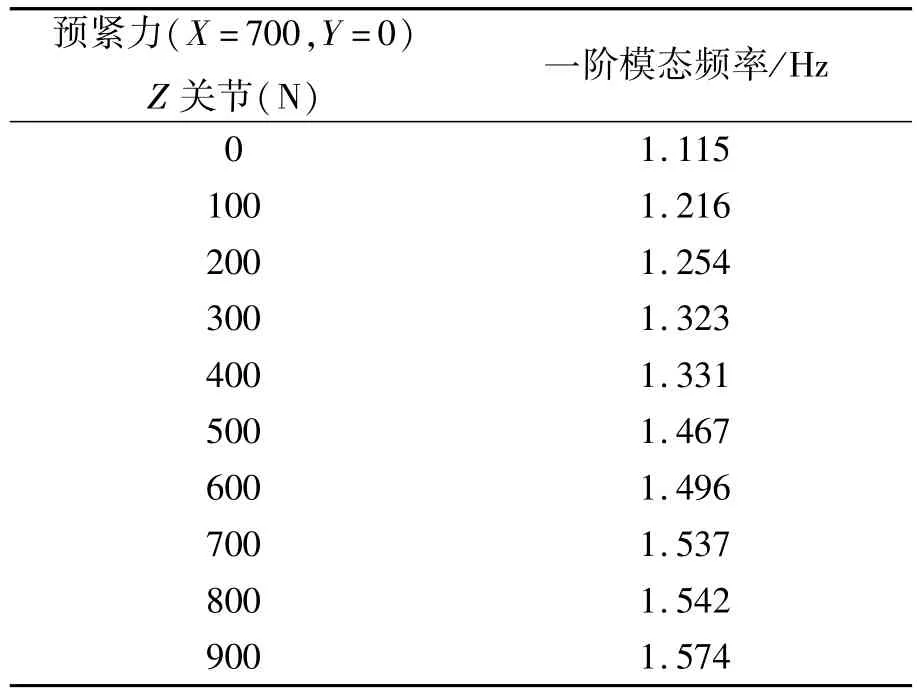
表4 系统一阶模态频率与Z关节轴承预紧力关系（X=700，Y=0）Tab.4 Relationship between preload of Z-joint bearing and first modal frequency of system（X=700，Y=0）

从表4可以看出，当Z关节轴承预紧力达到500 N时，臂式补偿机构与空间望远镜系统的一阶频率有较大提高，所以，Z关节轴承预紧力初步确定为500 N，可以进一步提高系统动态刚度。

当X关节轴承预紧力为700 N，Z关节轴承预紧力为500 N时，系统的动态刚度随Y关节轴承预紧力的关节见表5所示。

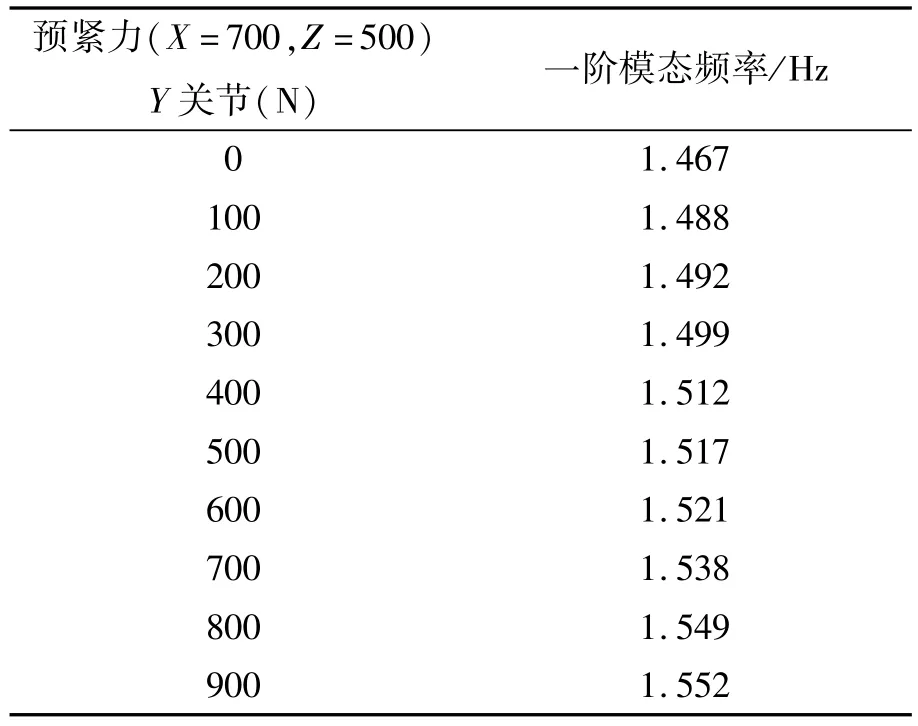
表5 系统一阶模态频率与Y关节轴承预紧力关系（X=700，Z=500）Tab.5 Relationship between preload of Y-joint bearing and first modal frequency of system（X=700，Z=500）

从表5中数据可以看出，Y关节轴承预紧力对系统动态刚度提高不大，因此，Y关节轴承预紧力可根据卸载力、启动力矩等灵活确定，选Y关节轴承预紧力为600 N。

5 结论

由臂式补偿机构控制空间望远镜的这种结构形式，会导致系统刚度很低。为了满足控制系统提出的结构系统高刚度要求，在系统结构形式确定的情况下，分析通过施加轴承预紧力来提高系统固有频率的可行性。通过理论分析及利用有限元分析的手段，对配对使用的角接触球轴承施加合适的预紧力，可以提高轴承的刚度，进而提高支撑系统的刚度。基于该思路，本文主要分析了轴承预紧力和轴承刚度、关节轴系刚度的关系，推导出了轴承预紧力与关节轴系刚度的关系表达式，并通过有限元分析的手段获得了轴承预紧力与系统固有频率的关系。证明在系统结构形式确定的情况下，对轴承施加合适的预紧力可以提高系统的刚度，同时为确定轴承最佳预紧力提供了有效的方法。对于文中所示系统，当X关节预紧力为700 N，Z关节预紧力为500 N，Y关节预紧力为600 N时，系统的基频在1.5 Hz以上，达到了预期目的。

［1］韩德一，梁波.惯性平台轴承预紧力及其刚度的计算分析［J］.中国惯性技术学报，1998，6(4)：38-60.

HAN D Y，LIANG B.Analysis and computation on the preloaded force and stiffness of bearing fixed in the inertial platform［J］.J.Chinese Inertial Technology，1998，6(4)：38-60.(in Chinese)

［2］ZVERV I，PYOUN Y S，LEE K B，et al..An elastic deformation model of high speed spindles built into ball bearings［J］.J.Materials Processing Technology，2005，170(3)：570-578.

［3］ALASRY A，ABEDI H.Kinematic and dynamic sensitivity analysis of a three-axis rotary table［J］.IEEE，2003 2：1147-1152.

［4］ALFARES M A，ELSHARKAWY A A.Effects of axial preloading of angular contact ball bearings on the dynamics of a grinding machine spindle system［J］.J.Materials Processing Technology，2003，136(1-3)：48-59.

［5］李朝辉，陈波.月基对地观测跟踪转台设计与分析［J］.光子学报，2010，39(12)：2215-2219.

LI ZH H，CHEN B.Development of lunar pointing mounts for imaging to the earth［J］.Acta Photonica Sinica，2010，39 (12)，2215-2219.(in Chinese)

［6］王智，李朝辉.月基极紫外相机光机结构设计［J］.光学精密工程，2011，19(10)：2427-2433.

WANG ZH，LI ZH H.Optical-mechanical structure design for lunar-based extreme ultraviolet camera［J］.Opt.Precision Eng.，2011，19(10)：2427-2433.(in Chinese)

［7］王智.基于碳纤维复合材料的月基极紫外相机照准架结构设计［J］.中国光学，2012，5(6)：590-595.

WANG ZH.Design of CRFP collimation frame structure of lunar-based EUV camera［J］.Chinese Optics，2012，5(6)：590-595.(in Chinese)

［8］张景旭.大型跟瞄架方位轴系的研制［J］.光学精密工程，1996，4(2)：73-77.

ZHANG J X.Development of vertical axial system for large tracking and pointing mount［J］.Opt.Precision Eng.，1996，4(2)：73-77.(in Chinese)

［9］田学光，田兴志，刘轩，等.大型精密转台高精度角度微驱动装置研制［J］.光学精密工程，2010，18(5)：1112-1118.

TIAN X G，TIAN X ZH，LIU X，et al.Development of angular micro driving device for large-scale and high accurate turntable［J］.Opt.Precision Eng.，2010，18(5)：1112-1118.(in Chinese)

［10］李为民，王海涛.轴向定位预紧轴承刚度计算［J］.河北工业大学学报，2001，30(2)：15-19.

LI W M，WANG H T.Rigidity calculation of axial position preload bearings［J］.J.Hebei University of Technology，2001，30(2)：15-19.(in Chinese)

［11］郭向东，王燕霜.轴承预紧力-系统固有频率及跨距关系的研究［J］.轴承，2013，4：30-33.

GUO X D，WANG Y SH.Research on relationship among bearing preload，system natural frequency and span［J］.Bearing，2013，4：30-33.(in Chinese)

［12］SHAN X B，XIE T，CHEN W SH.Novel approach for determining the optimal axial preload of a simulating rotary table spindle system［J］.J.Zhejiang University Science A，2007，8(5)：812-817.

Analysis on the relationship between bearing preload of spatial arm compensation mechanism and system stiffness

WANG Zhi*，GUO Wan-cun
(Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China)

When the spatial telescope tracks the target on the orbit，move and rotation will occurr between the visual axis of the telescope and target(namely pointing deviation and oscillation)due to all kinds of factors in space.In order to compensate above errors，the arm compensation mechanism is designed to compensate the errors between the visual axis and the target.Because the size and weight of the arm compensation mechanism are restricted severely，and the size of the telescope is huge and its weight is more than 3 000 kg，this configuration results in lower stiffness of the system.In order to satisfy higher machinery stiffness required by the control system，the feasibility is analyzed to improve system stiffness through forcing preload on bearing after the system configuration is confirmed.This paper studies on the relationship among bearing preload，bearing stiffness and system stiffness，and the relationship curve between bearing preload and system natural frequency is obtained.The analysis proves that forcing an appropriate preload to bearing can improve system stiffness on the condition that the system configuration is confirmed，and it is also an effective method to confirm the optimumbearing preload.

arm compensation mechanism；bearing；preload；stiffness

TH133.3

A

10.3788/CO.20140706.0989

2095-1531(2014)06-0989-07

王 智(1978—)，男，山东寿光人，博士，副研究员，2000年于长春光学精密机械学院获得学士学位，2003年于长春理工大学获得硕士学位，2006年于中国科学院长春光学精密机械与物理研究所获得博士学位，主要从事航天光学遥感器的光机结构设计、空间机器人结构设计等方面的研究。E-mail：wz070611@126.com

郭万存(1985—)，男，湖北随州人，硕士，助理研究员，2008年于中国地质大学获得学士学位，2011年于中国科学院长春光学精密机械与物理研究所获得硕士学位，主要从事航天光学遥感器的结构设计及优化、力学分析及力学试验等方面的研究。E-mail：guo333806@163.com

2014-09-18；

2014-11-17

国家自然科学基金资助项目(No.61108066)

*Corresponding author，E-mail：wz070611@126.com