干涉测量波面重构DCT算法研究

王永伟,艾 华,卓仁善,曹艳波

(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033；2.中国科学院大学,北京 100049；3.空军驻长春地区军事代表室,吉林 长春 130012)

干涉测量波面重构DCT算法研究

王永伟1,2,3,艾 华1*,卓仁善1,曹艳波1

(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033；2.中国科学院大学,北京 100049；3.空军驻长春地区军事代表室,吉林 长春 130012)

采用一种空间移相干涉仪测量凹形非球面反射镜光学表面，使用偏振元件和多幅图像同步采集实现移相，并对测量得到的干涉条纹采用基于离散余弦变换的相位解包裹算法，对不连续相位分布采用非加权的最小二乘法进行优化目标函数，最终重构出被测光学表面的面形。这种结构形式的干涉仪具有一定的抗振能力，同时在数字图像处理上优化了算法，能够快速稳定地得到被测面形，而且对硬件要求不高。结果表明：这种算法能够适用于非实验室条件下的光学测量，在一定干扰条件下可以达到较高的测量精度。

干涉测量；离散余弦变换；相位解包裹；最小二乘法；曲面拟合

1 引言

干涉测量的精度随着精密加工和数字图像处理技术的发展而得到了不断地提高。通过移相技术可以获得测量表面不同相位的面形信息；通过光电探测。图像处理和计算机运算等手段，可以得到高分辨率的面形信息。空间移相技术可以同步地得到多幅不同相位的干涉条纹，通过合成算法和相位解包裹运算，可以得出准确的测量信息，并且不受振动等外界条件的干扰［1-4］。通过对同步采集的干涉条纹进行合成运算，可以得到测量表面的相位分布。由于相位分布是根据干涉条纹计算得出的，其必然存在相位的周期重复缠绕，因此需要通过一定的算法对相位进行解缠绕运算。相位解缠绕又称为相位解包裹运算，是合成孔径雷达干涉测量、光学干涉测量、波前补偿以及医学核磁共振图像处理等领域图像信息获取的一个重要步骤，目前比较成熟的相位解包裹算法主要包括3种：基于路径积分的算法、最小范数算法和网络规划算法。这3种算法都有各自的优缺点，在计算速度与计算精度两方面进行折中，根据具体情况加以选择。其中基于路径积分的算法是从一个已知真实相位值的像元点开始，对其邻近像元点进行包裹相位差值的累计，通过迭代扩展直到图像上所有像元点的相位信息都得到解包裹，这种算法通过最小二乘法使包裹函数的离散偏差微分和解包裹函数的离散偏差微分的差值达到最小。本文介绍了一种偏振移相的干涉测量光路，采用四步法移相，得到相位差依次为90°的四幅干涉图，然后对干涉图进行基于离散余弦变换(DCT)的相位解包裹算法，该算法是一种基于优化问题的非加权最小二乘算法，减少了干涉图中无效点在解包裹运算中的影响，重构出被测镜面的面形图，这种方法适用于对光学镜面干涉测量的精确面形重构，且可以抵消测量过程中的部分随机振动［5-9］。

2 干涉测量的信息获取

干涉测量使用的仪器主要是干涉仪，目前使用比较成熟的用于大口径光学表面测量的干涉仪主要有Fizeau型和Twyman-Green型两种结构形式，前者由于共光路结构，能够抵消部分测量误差，但是对标准镜要求比较严格；后者参考镜要求可以相对简单，而且通过镜头的选择可扩展测量范围。本文设计的干涉仪结构采用Twyman-Green型，其结构形式如图1所示。

图1 Twyman-Green干涉仪的结构示意Fig.1 Schematic diagram of the Twyman-Green interferometer

被测镜面为曲率为R=-0.008，二次曲面常数K=-0.15的凹形非球面反射镜(本文镜面为理想镜面，不包含加工误差)。相干光源采用窄线宽半导体激光，波长为780 nm，其为线偏振光，偏振方向与图示光学主截面成45°，经过偏振分光棱镜(PBS)后，分成幅值相等的两个分量：反射的s矢量和透射的p矢量，s矢量经过两次1/4波片(QWP)和参考镜面后，变成p矢量；透射的p矢量经过两次1/4波片(QWP)和透镜组及被测镜面后，变成s矢量；这两个振动方向垂直的线偏振光再次经过偏振分光棱镜(PBS)后，一起再通过1/4波片(QWP)，变成两个旋向相反的圆偏振光，再经过消偏振分光棱镜(NPBS)和两个偏振分光棱镜(PBS)后，实现空间移相，得到相位依次相差90°的干涉条纹，如图2所示，对应点的光强分布如下式所示：

图2 空间移相法测量得到的干涉图Fig.2 Interferograms measured from space phase shifting method

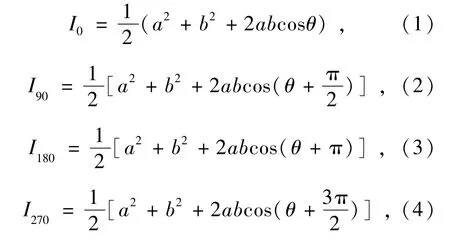
式中：θ为被测镜面的位相分布，a，b分别为对应于参考镜和被测镜的经过两次偏振分光棱镜的相互垂直的振动矢量的幅值，通过联立式(1)～(4)，可以解出：

干涉仪测量表面面形是根据被测光学表面与标准参考表面的光束干涉而产生包含光强信息的干涉条纹，通过将光强信息转化为相位信息来得到被测光学表面的空间信息，即表面面形，而实际上通过干涉条纹运算所得到的相位差被限制在［-π，+π］之间，如何恢复模糊的相位周期而获得目标的绝对相位差就需要进行相位解包裹运算。

3 基于DCT算法的相位解包裹

通过上述偏振移相的方法得到相位差依次为90°的四幅干涉条纹后，一般要进行滤波处理以消除部分非共模量噪声［10］。这种方法一般称为四步法，其对CCD的二次非线性响应和多光束干涉效应有很好的抑制作用，并且同步采集对环境扰动和结构振动有一定抗性。处理得到的干涉条纹在满足采样定理的条件下，才能进行相位解包裹运算。而实际测量的干涉图即使经过了滤波处理，还会残余一些噪声，如斑点、低调制度、随机扰动、表面突变等使得局部区域不满足采样条件，这就要求相位解包裹算法具有一定的除噪声功能，在这里路径追踪算法和优化目标的算法都得到了很广泛的应用。而基于DCT算法的相位解包裹正是基于优化算法而发展出来的。

相位解包裹运算的评价指标有结果的一致性和精确性［11-12］。结果的一致性是指，假设某点的相位解包裹值为φi，j，用这一方法去求解任意另外一点的解包裹相位值φi，j时，φi，j不会有两个或者两个以上的结果，一致性也可以理解为解包裹运算要与运算选取的路径无关；结果的精确性是指，用这一方法求得的解包裹相位φi，j要尽量逼近原始相位。当干涉图像中包含噪声、重叠或遮挡等干扰时，它们会引起相位解包裹结果的不一致和时间上的去相干等现象，因此简单积分会产生误差传递和累积。利用最小二乘法，求取与包裹相位斜率偏差平方和最小的相位曲面，能够有效抑制噪声点的影响，从而保证解包裹所得的曲面的连续性。优化目标函数J可表示为：

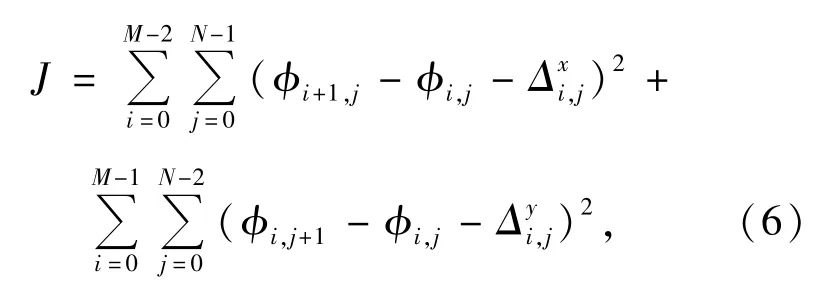
Ghiglia提出了利用DCT来求解Poisson方程(7)，主要采用迭代非加权算法，以减少干涉图中无效点或者坏点在解包裹位相中的影响，这种算法不依赖于积分路径，解包裹的结果是连续的，不存在无解的区域，容易实现因此实用性很强。

利用二维DCT对定解方程进行求解，得到：

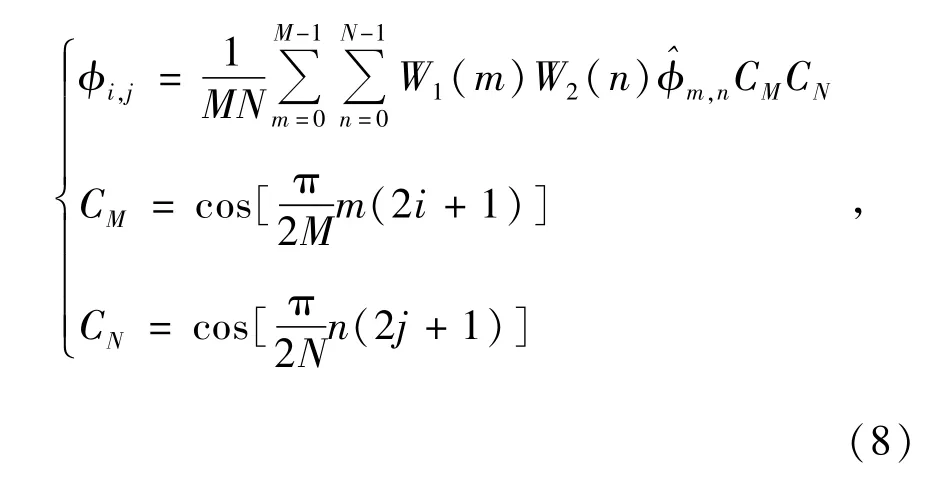
式中：

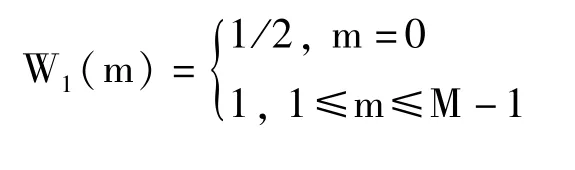
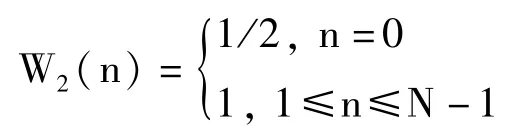
一般基于DCT算法的波面相位解包裹的计算流程如框图3所示，算法主要分为5个步骤，需要经过一次滤波处理，同时算法本身对除边界外的噪声有一定抑制作用。

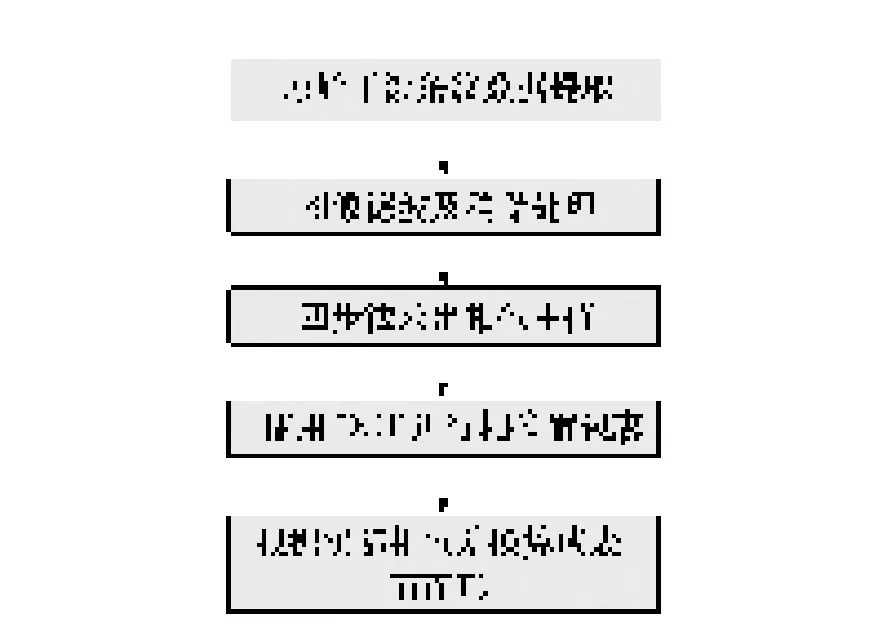
图3 DCT算法波面重构流程框图Fig.3 Schematic flow of the wavefront reconstruction by DCT algorithm

4 干涉条纹的面形重构计算结果

对上述Tywman-Green干涉仪测量得到的干涉条纹进行波面重构，对于实际测量得到的干涉图要先进行去除噪声的处理，部分非共模噪声可以通过图像滤波的方法可以消除，共模噪声则可以通过不同相位的差分运算得以消除。经过消噪处理后，在干涉图上叠加相同的掩模，计算得到初始的幅值分布和相位分布，分别如图4和图5所示。

图4 移相合成的初始幅值分布Fig.4 Initial magnitude distribution from phase shifting synthesis

图5 移相合成的初始相位分布Fig.5 Initial phase distribution from phase shifting synthesis

通过简单迭代算法，由初始相位分布，采用DCT算法进行相位解包裹运算，可以得到解包裹后的相位分布，结果如图6所示。通过对比初始相位可以看出，整个波面的相位分布由不连续变成连续分布，边缘出现毛刺的原因是由于掩模边缘与初始相位的重叠位置出现相位数值的跃变，进而导致计算结果的不收敛，这些数值基本不影响测量结果，适当选择掩模的范围可以减小边缘毛刺的影响。计算过程根据处理的像元尺寸的大小而变化，但是对计算机的硬件要求不高［13-14］。

图6 DCT解包裹后的相位分布Fig.6 Phase distribution after phase-unwrapping based on DCT

由于相位分布和波面面形是线性关系ΔH= Δθ·λ/(4π)，可以得到波面面形如图7所示(x，y坐标分别表示像元点位置)，从结果可以看出，面形基本符合非球面的特征参数，由于算法在边界处的不稳定性，会出现一定的毛刺区域，可以在后期处理中通过附加掩模的方法得到平滑的结果。通过Zernike多项式拟合的方法可以得到波面像差分量，可以用于定量分析光学表面的特征。

图7 DCT解包裹后的重构面形Fig.7 Reconstructed wavefront after phase-unwrapping based on DCT

5 结论

在对精密光学元件及光学系统的检测方法中，干涉测量是目前最为有效的超精密检测手段之一。空间移相干涉仪由于原理具有很好的抗干扰能力，成为目前主流的干涉测量设备。干涉测量得到的结果是干涉条纹，对干涉条纹的处理有多种数字图像处理算法，相位解包裹算法是得到连续面形的常用方法。本文针对一种空间移相的Twyman-Green结构干涉仪对光学表面进行干涉测量，采用空间移相得到相位差依次为90°的4幅干涉图，这种移相方法实现同步四步法采集干涉图像，可以消除部分环境扰动与振动带来的测量误差，从而提高了系统测量精度；并对干涉图采用基于DCT的方法，对干涉条纹进行非加权最小二乘法的相位解包裹运算，最后重构出了被检测光学表面(非球面)的面形图，结果表明这种易于实现、快速的算法在硬件条件有限的情况下也能高效的得到计算结果，对复杂条件下的光学检测提供一种可选的技术方案。

［1］CREATH K.Phase-measurement interferometry techniques［J］.Progress Optics，1988，10（26）：349-398.

［2］WYANT J C.Interferometric optical metrology：basic system and principles［J］.Laser Focus，1982，18（1）：65-71.

［3］BURNING J H，HERRIOTT D R.Digital wavefront measuring interferometer for testing optical surfaces and lenses［J］.Appl.Opt.，1974，13（11）：2693-2703.

［4］DECK L L，SOOBITSKY J A.Phase-shifting via wavelength tuning in very large aperture interferometers［J］.SPIE，1999，3782：432-442.

［5］莫卫东，范琦，贾晋超，等.非球面检测中最佳入射球面波和最佳参考球面波的确定［J］.中国光学，2012，5(3)：263-268.

MO W D，FAN Q，JIA J CH，et al..Determination of optimum positions of incident spherical wave and reference spherical wave in testing aspheric surface［J］.Chinese Optics，2012，5(3)：263-268.(in Chinese)

［6］杨亚威，李俊山，张士杰，等.基于视觉对比敏感度与恰可察觉失真感知的图像复原［J］.光学精密工程，2014，22 (2)：459-466.

YANG Y W，LI J SH，ZHANG SH J，et al..Image restoration based on visual contrast sensitivity and just noticeable distortion perception［J］.Opt.Precision Eng.，2014，22(2)：459-466.(in Chinese)

［7］SCHWIDER J，BUROW R，MERKEL K.Digital wavefront measuring interferometry：some systematic error sources［J］.Appl.Opt.，1983，22(21)：3421-3432.

［8］KERR D，KAUFMANN G H，GALIZZI G E.Unwrapping of interferometric phase-fringe maps by the discrete cosine transform［J］.Appl.Opt.，1996，35(5)：810-816.

［9］GHIGLIA D C，PRITT M D.Two-Dimensional Phase Unwrapping Theory，Algorithms，and Software［M］.New York：John Wiley&Sons，Inc，1998.

［10］QUIROGA J A，BERBABEAU E.Phase-unwrapping algorithm for noisy phase-map processing［J］.Appl.Opt.，1994，33 (29)：6725-6731.

［11］DE VEUSTER C，SLANGEN P，RENOTTE Y，et al..Disk-Growing Algorithm for phase-map unwrapping：application to speckle interferogram［J］.Appl.Opt.，1996，35(2)：240-247.

［12］HUNTLEY J M，SALDNER H.Temporal phase-unwrapping algorithm for automated interferogram analysis［J］.Appl. Opt.，1993，32(17)：3047-3502.

［13］GHIGLIA D C，ROMERO L A.Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods［J］.J.Opt.Soc.Am.A，1994，11(1)：107-117.

［14］刘江，苗二龙，曲艺，等.基于光强自标定移相算法检测光学面形［J］.光学精密工程，2014，22(8)：2007-2013.

LIU J，MIAO E L，QU Y，et al..Measurement of optical surface based on intensity self-calibration phase-shift algorithm［J］.Opt.Precision Eng.，2014，22(8)：2007-2013.

Wavefront reconstruction of interferometry by DCT algorithm

WANG Yong-wei1，2，3，AI Hua1*，ZHUO Ren-shan1，CAO Yan-bo1
(1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，Changchun 130033，China；2.University of Chinese Academy of Sciences，Beijing 100049，China；3.Air Force Military Delegate Office in Changchun，Changchun 130012，China)

We use a type of interferometer with space phase-shifting technique to measure the optical surface of the concave aspheric mirror in this paper.By using polarized elements and multi-image collected in synchronism we implement the phase-shifting process，and we adopt the phase unwrapping algorithm based on discrete cosine transform(DCT)onto the interferograms that we measured.For the discontinuous phase distribution，we adopt the un-weighted least square method to optimize the objective function，and finally reconstruct the wavefront surface of the measured optical surface.This type of interferometer has the capacity of anti-vibration，and can optimize the algorithm in the digital image processing procedure，so we can get the measuredsurface shape rapidly and steadily，and it is no need for high performance hardware.This approach can be used as optical measurement out of laboratory conditions，and we can get high measuring precision under the condition of disturbance existing.

interferometry；discrete cosine transform(DCT)；phase unwrapping；least square method；surface fitting

TP394.1；TH691.9

A

10.3788/CO.20140706.1012

2095-1531(2014)06-1012-07

王永伟(1983—)，男，山西汾阳人，学士，工程师，2006年于空军工程大学获得学士学位，主要从事光电测量设备等方面的研究。E-mail：yongwei.516@163.com

卓仁善(1960—)，女，吉林省吉林市人，研究员，硕士生导师，1986年于东北工学院获得硕士学位，主要从事光电经纬仪结构设计方面的研究。E-mail：zhuornshan@sina.com

艾 华(1961—)，男，吉林长春人，研究员，博士生导师，1984年于长春光学精密机械学院获得学士学位，主要从事微纳量位移测量和半导体激光器在光学仪器中的应用方面的研究。E-mail：aih@ciomp.ac.cn

曹艳波(1984—)，男，湖北黄石人，硕士，助理研究员，2009年于华中科技大学获得硕士学位，主要从事精密仪器设计与分析方面的研究。E-mail：pinocchio84@163.com

2014-09-15；

2014-10-17

长春光机所领域前沿创新项目(No.Y26532B120)

*Corresponding author，E-mail：aih@ciomp.ac.cn