矩形离轴非球面反射镜双摆法加工与检测

宋淑梅

(中国科学院长春光学精密机械与物理研究所，吉林长春130033)

1 引言

离轴非球面反射镜具有无中心遮拦、可改善像质、增加系统的相对口径和简化系统结构等优势，在大型望远镜、空间相机、军事侦察等现代化光学系统中是不可替代的。某些特殊的光学系统如空间光谱仪不仅要求光学系统具有质量轻、大视场、高分辨率、无中心遮拦，而且还需具有矩形通光孔径。因此，采用矩形离轴非球面轻质反射镜的光学系统是满足上述要求的最佳选择。矩形离轴非球面镜的光学加工除具有一般离轴非球面的加工难点外，因其远离母轴轴心的外侧边两直角区域存在急剧的面形偏差且为孤立区域，使该两处的加工又成为一个难点。目前，离轴非球面光学元件的加工［1］主要有传统和现代加工技术。传统的经典方法有两种:一是采用先加工出全口径母镜，再从加工完成后的母镜上切割出所需要的部分。这种方法的好处是解决了旋转对称问题，但具有一定的局限性;二是通过高级技师的手工修磨完成对离轴非球面光学元件的加工。现代加工技术主要有计算机控制光学表面成形技术、应力盘抛光技术、磁流变抛光技术以及离子束抛光技术［2］等，在光学非球面加工领域发挥了重要的作用。尽管如此，针对具有矩形通光孔径的高精度矩形离轴非球面镜的光学加工，上述方法依然难以尽如人意。如计算机控制光学表面成形技术加工产生的中频误差较大，应力盘抛光技术复杂、成本较高，适于大口径镜面的加工。离子束抛光技术加工效率较低，一般仅用于达到一定精度后的后期抛光加工且产生的高频误差较大。因此，具有高效率低成本的高精度矩形离轴非球面加工工艺是一个有着实用价值的研究方向。

双摆动加工方法是由经典的修带抛光技术与现代数控加工技术相结合发展而来的一种高精度、低成本的工艺方法。对于离轴非球面镜的加工，双摆动加工方法通过改造机床，将工作台旋转运动改为往复摆动，靠摆动实现磨盘与工件的相对运动，并采用特定的工艺方法实现以单块独立加工方式完成离轴非球面镜的加工。

2 矩形离轴非球面镜加工

2.1 矩形离轴非球面镜加工特点

通光口径为矩形的离轴非球面，除了存在一般离轴非球面无旋转对称轴的加工难点外，还在其远离母轴的外侧边角处具有急剧面形偏差。此两处不仅非球面梯度很大，而且每处区域面积均很小，使得磨盘姿态很难控制，采取局部单独修磨的方式加工极易造成严重的局部误差，导致该两区域虽然修磨量相同但修磨后两者之间面形相差很大而且与整体面形的偏离也可能很大，甚至在光学检测过程中经过该两区域的光线难以进入到检测视场之内。所以，矩形离轴非球面加工难度更大。为解决上述加工难题，根据离轴非球面性质设计出双摆法加工工艺，并改造成功双摆动抛光机床使该工艺方法得以实施。该设备已获国家发明专利授权。

2.2 双摆动加工方法介绍

通过普林斯顿假设和线性理论推导，可以建立如下关于材料去除量的数学模型［3］:

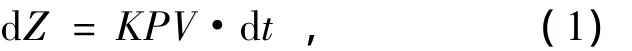
式中，K为比例常数，与加工过程参数(加工温度、磨头材料、工件材料等)有关，P为磨盘与工件间的相对压力，V为磨盘与工件间的相对运动速度，t为磨盘在工件加工区域的驻留时间，z为工件材料去除量。由上式可见，材料去除量与相对压力、相对运动速度和驻留时间均呈正比关系。进一步的研究得出，当工作压强保持不变时，光学表面的材料去除量Z(x，y)近似等于磨盘去除函数R(x，y)(单位时间内的材料去除量)与加工区域内驻留时间D(x，y)沿运动轨迹的二维卷积［2］:

式中，＊＊表示二维空间卷积［4］。

因此，针对非球面工件被加工表面上不同的材料去除量，磨盘与工件的相对运动轨迹在加工中起着举足轻重的作用［5-7］。

为解决离轴非球面无旋转对称轴的加工难题，研究一般旋转对称非球面性质［8］，尽管其表面上任何一点都是双曲率的，即它的子午曲率和弧矢曲率不相等，且距中心位置不同的环带区内的曲率也各不相等，但以其母镜旋转对称轴为中心的同一环带上的弧矢曲率及子午曲率却是各自相等的。也就是说，同一标准球面上以母镜旋转对称轴为中心的同一环带具有相同的修磨量。利用这一特点设计磨盘与工件的相对运动轨迹，有助于找到加工离轴非球面的科学高效的加工方法。双摆动加工方法依据这一特点设计离轴非球面加工工艺方案［9］:以工作台摆动轴为离轴非球面母轴，将成形后的被加工离轴非球面镜按其离轴量的设计要求定位于数控旋转工作台上，使其随工作台数控摆动，形成绕母轴(工作台旋转轴)按加工所需要的角度往复摆动的运动形态。并使抛光盘沿工作台径向往复摆动，工件得到利于加工的运动轴。

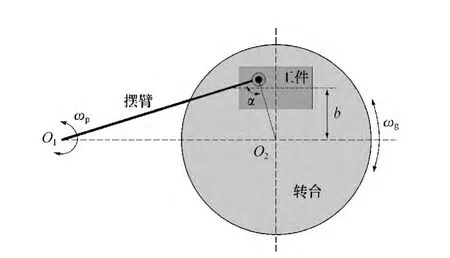
图1 双摆动加工原理图Fig.1 Manufacturing principle of the double-swing method(DSM)

为实现这种工艺方法，设计并成功改造了数控双摆动加工机床。该机床主要由精密数控转台和摆臂机构组成，加工原理如图1所示。精密转台由伺服电机驱动通过曲柄连杆机构可绕轴O2进行数控旋转或往复转动，摆臂由四连杆机构经电机驱动可绕摆轴O1往复摆动。加工时将离轴非球面工件安装在机床工作台上，使其中心与工作台中心距离为非球面的离轴量b。并使其绕工作台中心(母轴)按加工需求数控往复摆动一定的角度，同时使抛光盘由摆臂带动沿工作台径向以较小的摆幅往复摆动。通过对加工工艺参数设计，如工作台摆速、摆轴摆速及摆幅、抛光盘大小及形状、压力及驻留时间等的调整，实现对工件上的任何位置的修磨，包括对陡度极大的边角处的修磨。从而加工出满足要求的离轴非球面镜。

综上所述，双摆法将工作台旋转轴变为摆动轴，使得离轴非球面的加工由原来的工件不动变为往复摆动，既增大了工件与磨盘的相对运动速度，提高了加工效率，又为加工工艺提供了更多种的选择。

2.3 双摆法应用

非球面加工过程中出现的误差类型主要分为球差、象散误差、彗差及局部误差等。双摆法对这些误差的修正都具有一定的优势。一般情况下，加工初期首先需要解决的是球差问题。只有加工到面形精度剩余球差较小时其它象差才能显现出来。球差在工件上表现为环带误差。现代光学所需要的离轴非球面镜通常都具有较大的相对口径，因此初始加工时工件往往都存在着相当大的环带误差。对于环带误差的修正，采用修带法加工最为经济高效。双摆法利用双摆式加工机床，将工作台旋转轴变为摆动轴，通过工作台往复摆动，可以对工件实现修带法加工。运动模式为:工件随工作台往复摆动的同时，磨盘在需要去除的环带区域沿工件径向小幅快速往复摆动。如此按每个环带象差大小逐一修磨，并循环往复，使得非球面面形快速收敛。

对于象散误差、彗差及局部误差的修正，过去比较普遍的加工方法一般是保持工件不动，使磨盘在面形误差的高点区域按去除量需要往复运动。这样仅靠磨盘运动的磨削加工去除效率较低，而采用双摆法加工增加了工作台运动，可以根据所加工工件面形误差情况，通过数控系统科学有效地控制工作台往复摆动的角度、速度及在某一位置的驻留时间等，再配合磨盘的调整和运动，制定更为高效合理的误差修正方案。

磨盘在离轴非球面加工中起着重要的作用。由于双摆法靠摆动实现磨盘与工件的相对运动，不需要磨盘自转，可根据工件修磨量大小修整磨盘区域分布状态，改变磨盘与工件对应位置的接触面积，从而在加工中得到相应的材料去除量。理论上，其他参数相同时，磨盘与工件表面的接触面积越大，单位时间内的材料去除量就越大。利用这一点双摆法可解决矩形离轴非球面镜远离其母轴轴心的外侧两边角区域的加工难题。例如，本文所加工的矩形离轴非球面镜，按所确定的起始球面成形后，初始加工时最大修磨量位置有3处，一处位于临近母轴方向的直边上的中心，另外两处即为前述的两个边角。该3处各自独立。而位于0.7环带附近处修磨量最小甚至为零。修磨量变化趋势为从近轴直边中心至0.7带渐小，从0.7带至远轴两边角急剧增大。磨盘设计时，采用大小与工件尺寸相近的磨盘，根据此工件修磨量的趋势对磨盘进行修整，使加工时磨盘与上述3个修磨量大的区域接触面积较大，产生较大的去除量，与0.7带附近修磨量小的区域接触面积较小，形成少磨或不磨的效果。另一方面，根据普林斯顿假设建立的上述材料去除量的数学模型可知，因工作台摆动时从中心至边缘线速度增大，加工中在工件的远轴两边角区域将产生较大的去除量。从而解决了矩形离轴非球面镜加工中远离其母轴轴心的外侧两边角区域的加工难题。同理，上述方法也同样适用于其它区域的误差修改。

除此以外，磨盘的形状、大小等均对离轴非球面加工有着较大的影响。一般情况下，初始加工时因需要的去除量较大，应选用较大磨盘增大研磨面积以提高加工效率，加工中期低频形状误差较为突出，应选用较小磨盘使被加工表面快速收敛，加工后期局部误差及中高频误差占主要方面，则采用大小磨盘相结合的加工方式。因为较小直径的磨盘能够更好地修正局部误差，使表面形状精度在较短时间内达到规定指标，但是它产生的表面波纹度比较明显，而较大直径的磨盘具有很好的平滑作用，可以有效地去除表面中高频残差。应用大小盘结合的方法既提高加工效率又利于得到较为平滑的表面面形。

磨盘与工件之间的相对运动关系在加工过程中的作用举足轻重。理论分析及实验证明当摆杆在工件上的摆动轨迹为径向(指向工件母轴)时磨削效率较高，而且有利于去除中频误差，通过对双摆动加工相对运动分析得出［10］，工作台摆速、摆轴摆速及摆幅、夹角α值决定二者间的相对运动轨迹。其中，摆轴摆速与工作台转速之比、摆臂与磨盘在工作台位置径向的夹角α决定了磨盘与工件相对运动路径轨迹趋势，摆轴摆幅决定了对工件的加工区域范围。进一步的分析研究表示，摆轴摆速与工作台摆速之比相同时，摆臂与磨盘在工作台位置的径向夹角α为π/2时，磨盘与工件的相对运动轨迹近似位于工件径向。所以，加工过程中应使摆臂与磨盘在工作台位置径向的夹角α为π/2左右。

类似地，设摆臂与磨盘在工作台位置径向的夹角α=π/2。分析得出摆轴摆速与工作台转速之比小于1时，相对运动轨迹近似位于工件切向;摆轴摆速与工作台转速之比大于1时，相对运动轨迹近似位于工件径向。加工过程中应使摆轴摆速与工作台转速之比大于1，即磨盘摆速大于工件转速。应该注意的问题是，转速比不能为整数，为整数时会产生相同的运动轨迹周期，使得工件的去除量不均匀，难以得到高精度的表面面形。

3 加工中的检测

检测是加工中的重要环节之一。加工过程需要检测数据指明加工方向。在该矩形非球面加工中，在研磨阶段采用面形轮廓测量技术，待面形误差达到0.002 mm(RMS)左右时，加工进入到抛光阶段。在抛光阶段采用零位补偿法作为检验手段。

补偿法是通过光学补偿器将理想平面波或球面波转换为垂直于被测非球面法线的非球面波，使补偿器出射波前与被测非球面反射波前共路，构成自准直检测光路实现对非球面的高精度检测［11］。图2为离轴非球面镜补偿检测示意图。

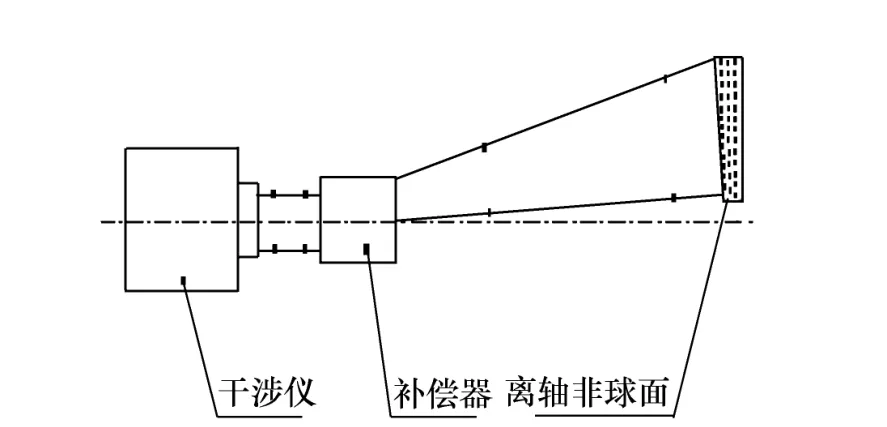
图2 离轴非球面镜补偿检测Fig.2 Offner testing for off-axis asphere mirror

补偿法检测对检验系统各单元的相对位置精度要求很高。首先，补偿器本身的加工和装配，各光学面的面形精度、元件中心厚度及间隔都必须满足设计要求;再者，补偿器与被测件间的相对位置必须正确。特别是检测光路的光学间隔决定着被加工非球面的面形参数，如顶点曲率半径、二次曲面系数及高次项系数。因此加工检测时除使检验系统各单元同心共路外，补偿器与工件定位格外重要。补偿器是旋转对称的，调整好后即可保持不动，因此以其为基准，只需对工件进行定位控制。作为空间物体，工件的位置有着6个自由度，包括沿z轴(光轴方向)平动，沿x、y轴(垂直于z轴且与z轴两两正交)平动，绕z轴转动及绕x、y轴转动。采用4测杆法［12］对工件6个自由度进行约束，以保证其在检测光路中的相对位置正确。所谓4测杆法是通过4个长度约束和2个高度约束实现对工件的位置控制。图3为该方法示意图。检测光路中，补偿器和工件的光学间隔可以转换为两者的间距来控制。在两者表面上各确定上下左右4个点并一一对应，则两者间该4个对应点距离可以精确计算得到。制作4根长度分别对应于上述距离的高精度测杆，配合使用高度尺，可以定位工件位置。光路调整时首先利用高度尺将矩形离轴非球面工件中心调至与补偿镜中心等高，并使矩形的上下两边保持水平(等高)，从而约束工件的y轴平移和z轴偏转;上下2根测杆约束x轴偏转和z轴平动;左右2根测杆约束x轴平移和y轴偏转。从而工件的6个自由度被约束，位置被确定。误差分析表明采用该方法所确定的工件位置满足设计要求。

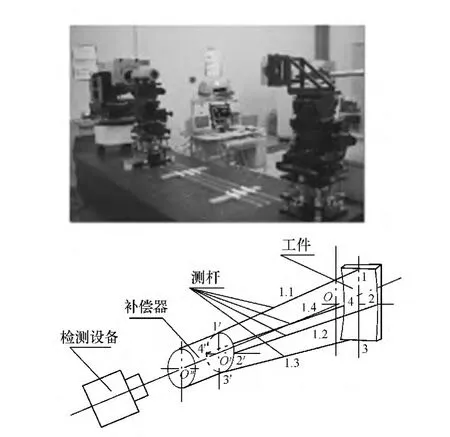
图3 4测杆法Fig.3 4-pole method

面形的光学检验采用刀口仪与干涉仪相结合的手段。刀口仪主要用于工件抛光加工初期的面形修改，它的测量灵敏度范围较广(星点大小可调)，细磨完成后工件的面形精度已进入其测量域。抛光初期工件面形误差主要表现为球差，用刀口仪检验更为直观、便捷。干涉仪主要用于抛光中、后期的面形修改。抛光中、后期工件面形误差主要表现为象散和局部误差。用干涉仪检测可直接测出实际面形误差状况和数值。在抛光加工的检测过程中始终采用4测杆法定位，以保证加工出的面形参数正确。

4 加工实例

应用双摆动加工法进行了某高分辨成像光谱仪共4块矩形离轴非球面反射镜加工，最终全部达到设计指标要求。以其中的主镜为例(如图4)，主镜尺寸为266 mm×118 mm，非球面设计指标为:二次项系数k为 －0.745，离轴量为65 mm，面形精度要求为λ/50(RMS，@633 nm)。该镜与比较球面偏离量为0.069 mm。设计加工流程如下(见图5)。

图4 离轴非球面镜Fig.4 Off-axis aspheric mirror

图5 加工流程图Fig.5 Manufacture process

首先按图纸外形尺寸要求及计算得到的比较球面半径铣磨成形。该反射镜的成形和最接近球面加工为常规工艺，在此不再赘述。因该非球面偏离量较大，细磨阶段就需要进行非球面修改。应用双摆动机床采用上述方法进行细磨加工，提高了加工效率，面形收敛很快。该阶段面形检验采用轮廓仪。待面形误差达到0.002 mm(RMS)左右时，加工进入到抛光阶段。初抛光阶段被加工工件表面误差主要为球差，在双摆动机床上以双摆动技术进行修带抛光，光学检验采用刀口仪，配合使用有限共轭距补偿器，并在检测光路调整中开始引入4测杆法，目的是控制面形参数满足设计要求。初抛光加工至面形精度达到0.2λ(RMS，@633 nm)左右时，进入精抛光阶段。精抛光加工过程中被加工工件表面主要误差是局部误差及中高频误差，则采用双摆法和手修相结合、大小抛光盘相结合的加工方式。光学检验采用干涉仪，配合使用无限共轭距补偿器，并在检测过程中继续采用4测杆法定位，以保证面形加工中面形参数正确。该镜最终加工完成后得到的结果面形精度为0.016λ，优于λ/50(RMS，@633 nm)的设计指标要求。图6为面形检测结果。

图6 面形检测结果Fig.6 Surface error testing result

5 结论

综合上面的分析及实际加工结果，在矩形离轴非球面加工中采用经典法与现代数控技术相结合的双摆动方法，较好地解决了矩形离轴非球面加工的技术难点，特别是远轴两角区域的加工难题，而且操作简单、成本低廉、去除效率较高、易于抑制表面中高频误差的产生得到较好的表面精度。该方法适合于尺寸不是很大的离轴非球面的加工。将该方法应用于口径为266 mm×110 mm矩形离轴非球面等元件的光学加工及检测，顶点曲率半径、二次曲面系数、离轴量等各项指标均达到技术要求，面形精度优于 λ/50(RMS，@633 nm)，且中频误差良好。该技术研究以及进一步开发利用对离轴非球面加工具有较好的应用价值。

［1］ 丁蛟腾，许亮，马臻，等.矩形口径离轴非球面镜的加工与检测［J］.光学技术，2012，38(5):607-610.

DING J T，XU L，MA ZH.Manufacture and test of rectangle aperture off-axis aspheric mirror［J］.Optical Technique，2012，38(5):607-610.(in Chinese)

［2］ 廖文林，戴一帆，周林，等.离子束抛光加工矩形离轴非球面镜［J］.国防科技大学学报，2011，33(1):100-104.

LIAO W L，DAI Y F，ZHOU L，et al..Ion beam figuring for rectangular off-axis aspheric mirrors［J］.J.National University of Defense Technology，2011，33(1):100-104.(in Chinese)

［3］ ROBERT A J.Fabrication using the computer controlled polisher［J］.Applied Optics，1978，17(12):1889-1891.

［4］ BOGDANOV A P.Automation of planning of technological process for machining high-precision optical components［J］.Sov.J.Opt.Technol，1984，51(9):539-541.

［5］ 邓伟杰，郑立功，史亚莉，等.离轴非球面抛光路径的自适应规划［J］.光学 精密工程，2009，17(1):65-71.

DENG W J，ZHENG L G，SHI Y L，et al..Adaptive programming algorithm for generating polishing tool-path in computer controlled optical surfacing［J］.Opt.Precision Eng.，2009，17(1):65-71.(in Chinese)

［6］ 郑立功，张学军，张峰.矩形离轴非球面的数控加工［J］.光学 精密工程，2004，12(1):113-117.

ZHENG L G，ZHANG X J，ZHANG F.NC surfacing of two off-axis aspheric mirrors［J］.Opt.Precision Eng.，2004，12(1):113-117.(in Chinese)

［7］ SONG C，DAVID W，YU G Y.Misfit of rigid tools and interferometer subapertures on off-axis aspheric mirror segments［J］.Optics Engineering，2011，50(7):073401.

［8］ 潘君骅.光学非球面的设计、加工与检验［M］.北京:科学出版社，1991:142-158.

PAN J H.The Design，Manufacture and Test of Aspherical Optical Surfaces［M］.Beijing:Science Press，1991:168-179.(in Chinese)

［9］ WANG P，LI J F，XUAN B，et al..Double-swing method used for polishing off-axis aspherical mirrors［J］.SPIE，2009，7282:728203.

［10］ 李俊峰，宋淑梅.应用双摆动技术加工离轴碳化硅反射镜［J］.光学 精密工程，2012，20(8):1671-1675.

LI J F，SONG SH M.Applying the double-swing method for manufacturing the SiC off-axis aspheric mirror［J］.Opt.Precision Eng.，2012，20(8):1671-1675.(in Chinese)

［11］ MALACARA D.Optical Shop Testing［M］.Hoboken:John Wiley＆ Sons Inc.，1978:444-454.

［12］ XUAN B，CHENG X P，WANG P，et al..Alignment of off-axis asphere and compensator with four poles［J］.SPIE，2009，7283:72830A.