统计分析方法在葡萄酒评价中的应用

●李焱

统计分析方法在葡萄酒评价中的应用

●李焱

文章针对葡萄酒的评价问题，利用统计分析的方法，建立了相应的数学模型，分析了葡萄酒感官指标与理化指标之间的联系，论证了葡萄酒感官评价的有效性。

t检验 主成分分析 聚类分析 相关分析 多元线性回归 逐步回归

一、问题的提出

在以往对葡萄酒进行评价中，主要是通过评酒员对葡萄酒的色、香、味的感官印象对葡萄酒进行打分从而评定葡萄酒的质量。但是由于评酒员间存在评价尺度、评价位置和评价方向等方面的差异，导致不同评酒员对同一酒样的评价差异很大，从而不能真实地反映不同酒样间的差异。所以需要建立更科学的评价体系对葡萄酒的质量进行定量评价。

聘请一批有资质的评酒员对葡萄酒进行品尝对其分类指标打分，然后求和得到其总分，从而确定葡萄酒的质量。已知酿酒葡萄与所酿葡萄酒的质量有直接的关系，葡萄酒和葡萄的理化指标可以反映部分葡萄酒和葡萄的质量。某一年份一些葡萄酒的评价结果为已知，在给出了该年份这些葡萄酒的和葡萄的成分数据的基础上建立数学模型讨论问题：两组评酒员的评价结果有无显著性差异，哪一组结果更可信？

二、问题的分析

对于此问题，要分析两组评酒员的评价结果有无显著性差异，并判断评价结果的可信度。可由不同组评酒员对不同类样本的葡萄酒评分，对这些数据进行统计分析。考虑到红、白葡萄酒之间的差异性，对这两种酒分别进行显著性差异检验。首先计算每组10位评委打分的均值作为对不同酒样本的评价值，利用检验对两组评酒员评价结果进行显著性分析。在显著性水平α=0.05下，建立检验模型，确定两组评委评价的显著性差异。

分析评价结果是否可信，主要依赖于两个指标：一是评价得分偏离标准值的大小；二是评价结果的离散性。由于聘请的品酒师是有一定资质的，因此可以把专家的平均水平作为品评的标准值。但考虑到品酒师对某个酒样品感官分析可能出现的失误性（引注），剔除20个品酒师对每类酒样品评分的异样点。对于剩余的得分求均值作为标准评价值的无偏估计。再用评价得分与标准值的偏差代表每组评酒员评价结果与标准值的接近程度；用方差来反映每组评价结果的离散程度。在与标准值的偏差不明显的情况下，比较评价方差的大小，作为综合判断每组评价结果的可信度的依据。

三、模型的假设与符号的说明

（一）模型的假设

1.假设评酒员对不同酒样品的评价得分服从正态分布。

2.假设我们对附件二缺省的数据的补充是合理的。

（二）符号的说明

Es表示标准值期望向量；

Fj表示第j号评酒员的标准评价得分；

xij表示第i个酒样品的第j项理化指标数据；

δj表示第j项理化指标的标准差。

四、模型的建立与求解

为了体现评委对红、白葡萄酒评价得分的区别，分别对两种酒建立显著性差异检验模型。

（一）评价得分的描述性分析

由问题的分析，以白葡萄酒为例通过对评价得分的数据处理，得到两组评酒员的检验数据表，如表1所示：

表1 评价得分的描述性分析

由该表可知：葡萄酒感官评价中，由于品酒员间存在评价尺度、评价位置和评价方向等方面的差异，同一评酒员对不同酒样品的评分偏差较大；不同品酒员对同一酒样品评分偏离平均值的分散范围也较大。从而不能真实地反映不同酒样品的差异，因此需要对评酒员评价结果做显著性差异检验。

（二）t检验模型的建立

由假设一，评酒员对不同酒样的评价得分服从正态分布。

设两组评酒员（ξ，η）对不同酒样的评分值为（ξ1，η1），（ξ2，η2），…，（ξn，ηn）,ξ服从N（a1，σ1），η服从N（a2，σ2），σ1和σ2均未知。为了检验评价结果的差异性，即需检验假设H0：a1=a2是否成立。

记Z=ξ-η，Zi=ξi-ηi（i=1,2，…，n），将Z看成一维的总体，Z1,Z2…，Zn为其样本，Z服从N（a1-a2,σ），记a1-a2=a。此时，原来对品酒结果的差异性检验，变成了对总体Z的数学期望a是否等于零的检验。

（三）t检验的一般步骤：

1.建立假设H0:a=0,H1:a≠0。

2.构造检验统计量。

利用统计软件SPSS19.0得到白葡萄酒检验的结果如表2所示：

表2 白葡萄酒t检验结果

由该统计指标sig＜0.05得出第一、二组的白葡萄酒评价结果有显著性差异。说明第一、二组的评酒师对于白葡萄酒的评价水平是不同的，需要对可信度进行分析。

（四）评价结果的可信度分析

由问题分析，评价结果是否可信，依赖于两个指标：评价得分与标准值期望差的欧氏距离，每组评价结果的方差。

1.确定评价标准值。以红葡萄酒为例，分析评酒员二和评酒员七对所有酒样品评分的差异值，进而分析评酒员对某个酒样品感官分析可能出现的失误性，如图1、图2所示：

图1 两组评酒员二对所有红葡萄酒酒样品评分

图2 两组评酒员七对所有红葡萄酒酒样品评分

由图1可知，评酒师二号对酒样品的评价得分离散性较大，感官分析具有一定误差性，评价得分的奇异点不利于标准评价值的确定。进而剔除20个品酒师对每类酒样品评分的异样点。对于剩余的得分求均值作为标准评价值的无偏估计。

生成标准值期望向量Es：Es=（E1，E2，…，En），其中，Ej表示第j号评酒员的标准评价得分。

2.确定可信度指标。分别取第i组（i=1,2）十名评酒员对白葡萄酒样的评价结果构成m×n矩阵（m=27，n=10）。该矩阵列向量均值为Eaj（1≤j≤n），则评价结果的期望向量：

定义两向量的欧氏距离反映与标准评价值的偏差：

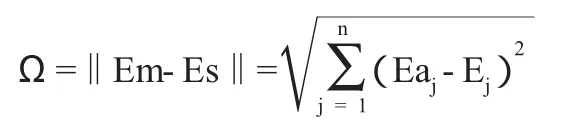
通过比较Ω大小即可确定每组评价结果和标准值的接近程度。如果Ω越接近0，说明此组评价结果与标准值很接近。进而初步判断两组评价结果的可信度。在评价结果可信度相差不大的情况下，利用评价结果的方差指标做进一步确定。

定义评价标准差向量：

3.确定两组评价结果的可信度。通过MATLAB编程计算分别得到第一组和第二组红、白葡萄酒的可信度指标，如表3所示：

表3 第一组和第二组红、白葡萄酒的可信度指标

由该表可知表中数据偏离标准值的指标Ω的值比较接近，就是红、白葡萄酒一、二组的期望与标准期望值差异不大，不能有效的辨别。需要进一步比较评价标准差向量模σ，而红、白葡萄酒均为第一组评价结果方差大于第二组，说明整体水平相同的情况下第一组的水平波动性大、稳定性小，可以得出第二组的红葡萄酒评价结果更可信。

五、结语

在此模型中，我们对两种葡萄酒分别进行了显著性差异检验，并在显著性水平0.05下，建立了t检验模型，确定两组评酒员评价的显著性差异，并分析了造成显著性差异的原因。综合考虑评价的期望与标准值期望之差和方差，分析评价了结果的可信性。

在未来的研究中，还可对数据做多因子方差分析，此方法可以不必考虑评酒员对不同酒样的评价得分是否服从正态分布。确定两组评酒员评价的显著性差异后，可以继续对不同评酒员不同酒样本的评分作描述性分析，确定单个评酒员差异性对评价结果的影响，并进一步深入分析。

[黑龙江省教育厅科学研究项目（12543073）]

[1]王文静.感官评价在葡萄酒研究中的应用[J].酿酒,2007(4)

[2]李记明.关于葡萄品质的评价指标[J].中外葡萄与葡萄酒,1999（1）

[3]李华，刘曙，王华，张予林.葡萄酒感官评价结果的统计分析方法研究[J].中国食品学报,2006(2)

[4]李运，李记明，姜忠军.统计分析在葡萄酒质量评价中的应用[M].酿酒科技,2009（4）

[5]李华，杨永锋，郭明浩，刘树文.影响干红葡萄酒感官质量的因素分析[M].生物数学学报,2005(2)

[6]李华,刘勇,强郭,安鹊,梁新红,康文怀,陶永胜.运用多元统计分析确定葡萄酒感官特性的描述符[J].中国食品学报,2007(4)

[7]韩中庚,郭晓丽,杜剑平.实用运筹学——模型、方法与计算[M]北京：清华大学出版社，2007

（作者单位：黑龙江科技大学理学院 黑龙江哈尔滨 150027）

F222

A

1004-4914(2014)09-203-03