基于信息熵的配准方法研究
上官晋太
(长治学院 计算机系,山西 长治 046011)
1 引言
图像处理和分析关键步骤就是图像配准。在进行目标识别、图像融合、图像对比等操作时,配准是预先要做的准备工作。由不同的成像设备产生的图像由于其成像机理的差异,会在分辨率和灰度属性等方面有不同的表现,这些图像通常称为多模态图像。近年来多模态图像信息融合已成为图像理解和计算机视觉领域中一项重要而有用的新技术[1-3]。
两个不同的传感器由于通过的光路不同,或者成像的机理上的差别,所得到的图像会存在相对旋转、平移和尺寸等方面的变化。这样的图像在几何结构上像素的对应关系不明确,所以无法进行直接融合。图像配准的目的和作用就是要确立这样的图像所包含的像素之间的对应关系,去除或抑制待配准图像和参考图像之间的不一致。
2 Shannon熵配准法
互信息的概念最早出现在Shannon的信息论里,它被用来度量两个随机变量包含对方信息量的多少。MIT人工智能实验室P.Viola和比利时的A.Collignon用互信息的方法对不同模态的图像进行了配准实验,由配准结果可知以互信息为配准测度可以用来配准不同模态的图像,它逐渐成为多模态图像配准领域重要的方法[4,5]。Nyquist和Hartley进行了早期的对信息论的研究工作,并发现了信息量的对数性质,提出了建立在概率模型基础上的信息度量,详细说明了信源、信道的特性,推出了信息量的表达式。
图像所包含的平均信息量可以用图像的信息熵来表示,给定两幅图像A 和B,根据信息论,图像熵H(A)、H(B)的定义为:
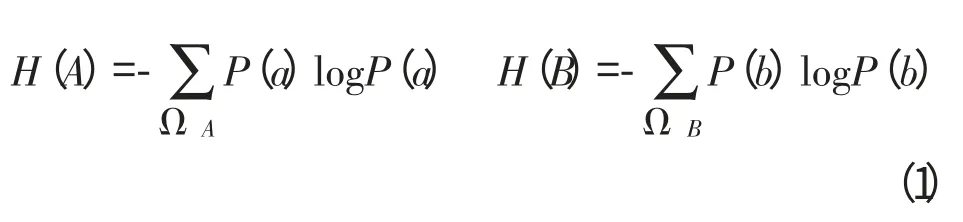
式中H(A)和H(B)分别是图像A 和图像B 的熵,a,b 表示图像像元的灰度值,ΩA和ΩB是图像A和B 的样本空间,p(a)、p(b)是图像灰度概率分布。Shannon熵的单位取决于对数底的选择,当选择“2”作为对数的底时,单位为比特(bit);当选择“e”为底时,单位为奈特(nat);当选择“10”为底时,单位为迪特(det)。
在已知一幅图像熵的情况下,另一幅图像中残留的平均信息量可以用图像的条件熵来表示,其定义为:
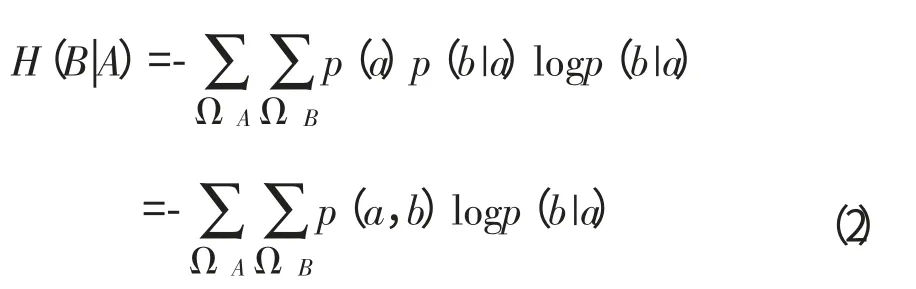
式中H(B|A)表示图像的条件熵,图像的联合概率分布用P(a,b)表示。两幅图像所保含的总信息量可以用图像的联合熵表示,其定义为:
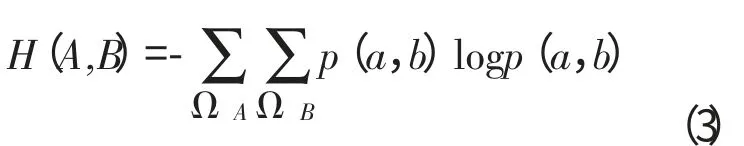
在两幅图像中相互包含对方的信息量是两幅图像共有的信息,它可以用互信息表示,其定义为:
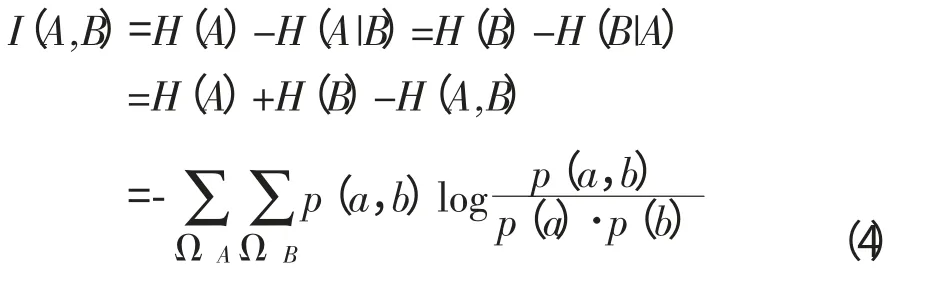
通过进一步研究,人们发现基于Shannon熵的方法虽然有配准精度高,不需要预处理且能自动配准的优点,但是也存在测度的值对重叠面积过于敏感的问题,为了提高这一类测度在配准过程中对重叠面积大小变化的鲁棒性,相继提出了Shannon熵测度的其它一些改进形式,这一类配准测度常被称为归一化互信息[6,7],它们的表达式如下:
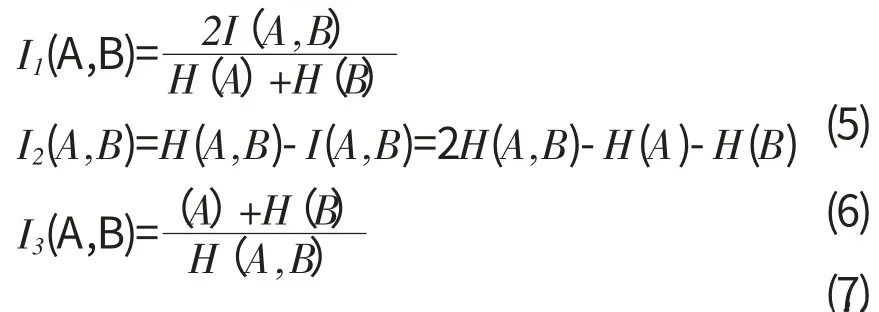
类似于I1可以写出另外一个归一化互信息的表达式:

在I1,I3,I4之间存在如下关系:
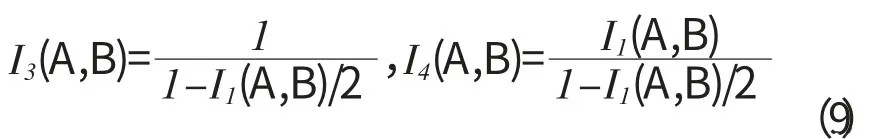
从上面可以看到I1,I3,I4之间是可以互相导出的,但是它们对于重叠面积变化的鲁棒性是不同的。I1(A,B)也叫熵相关系数。
3 配准实验
为了讨论不同配准测度的配准情况,分别用以上讨论的配准测度对实验图像进行配准实验。在本论文中所用到实验图像之一为人脑部磁共振图像,另一幅为非线性变化后的图像。
图1是用于配准的两幅图像,图2是不同配准曲线图。配准过程中一个图保持固定不动,另一个图分别向左右各移动40个点。可以看到图2中在完全配准点上,所有的曲线都是一个极值点,其中条件熵、联合熵和归一化互信息2在这个点取极小值,互信息、归一化互信息1和归一化互信息3在这点取极大值。
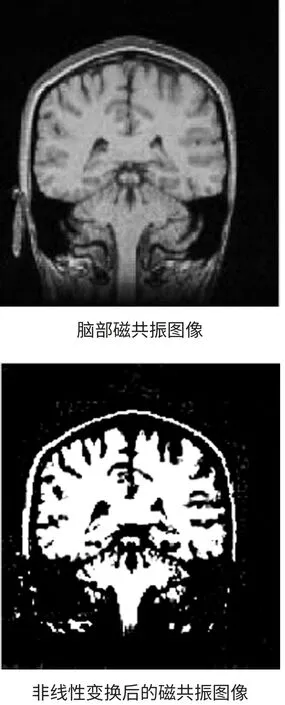
图1 脑部磁共振图像和非线性变换后的图
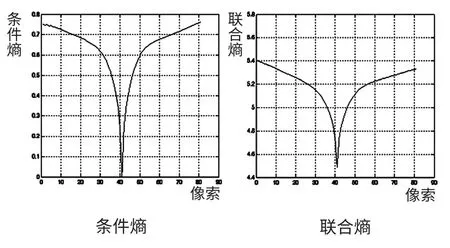
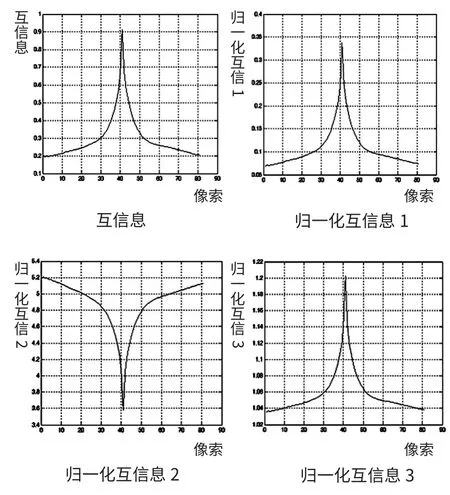
图2 不同配准测度的变化曲线
4 结论
基于信息熵的配准方法直接利用图像的灰度信息,具有配准精度高、不需要预处理且能自动配准的特点。配准精度高的原因除了信息熵本身的特点外,还因为配准时利用的是所有的灰度信息,信息利用率高;再者和基于特征的配准方法相比没有特征提取这个过程,所以也不存在特征提取所产生的误差。归一化互信息配准法具有更加好的稳定性,对重叠面积的变化不敏感,鲁棒性更好。
[1]高鹏.基于边缘和互信息法的红外图像配准[J].红外,2013,34(1):30-36.
[2]赵钰,朱俊平,亢娟娜.改进的区域互信息和小波变换的图像配准[J].计算机工程与应用,2013,49(21):152-155.
[3]杜晓刚,党建武,王阳萍,刘新国,李莎.基于萤火虫算法的互信息医学图像配准[J].计算机科学,2013,40(7):273-276.
[4]郭佳,李辉,王成,李思众.一种基于互信息的图像配准算法[J].传感技术学报,2013,26(7):958-960.
[5]吴泽鹏,郭玲玲,朱明超,贾宏光,宣明.结合图像信息熵和特征点的图像配准方法[J].红外与激光工程,2013,42(10):2846-2852.
[6]Brecht Heyde. Elastic Ⅰmage Registration Versus Speckle Tracking for 2-D Myocardial Motion Estimation: A Direct Comparison Ⅰn Vivo[J].ⅠEEE TRANSACTⅠONS ON MEDⅠCALⅠMAGⅠNG, 2013,32(2):449-459.
[7]冯雪芳,吴锡生.基于归一化边缘互信息与自适应加速粒子群的图像配准方法[J].计算机工程与科学,2013,35(1):11-123.

