电气工程专题教学中对创造性思维的培育
王 敏,袁 越,张新松,傅质馨
(1.河海大学能源与电气学院,江苏南京 211100;2.南通大学电气工程学院,江苏南通 226019)
0 引言
目前很多高校对本科电气工程专业的学生设置了专题教学,通过组织教学和科研经验丰富的教师就专业知识体系或专业前沿问题进行专题教学,使学生了解电气工程相关领域的技术发展现状,以启发和开拓他们的创新性思维,并为学生毕业后从事电力系统及相关领域的设计制造、运行维护和科学研究工作打下基础。
创造性思维贵在创新,在思路选择、思考技巧及思维方法上,具有独到之处,在前人的基础上有新的见解、发现和突破,从而具有一定范围内的首创性和开拓性。因此创新能力的培养要从创造性思维开发起步。在电力系统或其它专业的本科教学中,如何利用有限的课程教学内容和课内学时,建立完整知识体系的纵向和横向联系,高效率地完成对学生创造性思维的培养,提高大学课堂教育的质量,实现专业教学的目标是值得探讨的问题。
1 专题内容的选择
现代电力系统分析大多是以计算机为计算工具,因此建立描述电力系统的数学模型并进行准确的求解是现代电力系统分析的关键[1]。“电力系统分析”课程教学的基本思路也可以按照建立数学模型、求解数学模型和结果分析来进行[2]。
目前本科阶段的“电力系统分析”课程相关教材中基本上也包括了上述几方面的内容,但是缺乏纵向的联系和创新性思维的培育。教师在教学过程中如果不能具备完整的知识体系,也会忽略对学生创造性思维的培养,使得他们缺乏对电力系统分析思路的整体把握。短期内,学生难以把握学习重点,无法提高分析问题和解决问题的能力,学生长期缺乏创造性思维的开发,导致创新能力的欠缺。
电力系统从数学上讲是一个非线性动力学系统。由于系统中的元件包含旋转元件和静止元件,所建立的数学模型可能是基于不同的坐标系。在电力系统分析和计算中,由于电机的转子和定子之间有相对运动,因而建立的方程是一组以时间的周期函数为系数的微分方程,用解析法直接求解十分困难。同样,交流电机的控制也因此变得非常困难。因此线性代数的坐标变换理论在电力系统中应运而生。根据要研究的问题,挖掘其物理本质,可以完成参考坐标系的变换、相数的变换、对称分量和不对称分量的变换,从而实现简单有效的电力系统分析的计算以及电机的控制等。
以同步发电机基本方程为例,引入Park变换以后可以将电势方程从以时间的周期函数为系数微分方程组变换成一组常系数的微分方程,使得方程易于解析。同样,矢量控制就是通过坐标变换将感应电机模型转化为类似于直流电机的模型来进行控制,使在同步旋转坐标系下的定子电流两个相互垂直分量分别独立地控制转矩和转子磁链。
所以笔者从坐标变化的数学原理及其在电力系统中的应用出发,解决学生在电力系统分析学习中遇到的共性问题,提高他们把数学理论应用到电力系统研究中的能力,帮助其寻找分析和研究电力系统的基本思路。
2 坐标变换基本原理
电力系统研究中经常碰到的坐标变换,包括静止坐标系间的变换、旋转与静止坐标系间的变换、旋转坐标系间的变换和对称分量变换等。其中三相静止坐标系和两相静止坐标系间的变换,简称3s/2s变换(也称Clarke变换)、两相或三相静止坐标系和两相旋转坐标系间的变换,简称2s/2r及3s/2r变换(统称Park变换[3])。本文希望能够从坐标变换的数学原理出发,通过分析各类坐标变换的特点及其应用,解决以下问题:①为什么应用此类坐标变换?②坐标变换中会遇到什么问题?是如何解决的?③对我们的工程实践或科研有什么启发?再将此类问题推广到电力系统的其它领域,从而完成课堂教学中的创造性思维的训练。
2.1 坐标变换的数学原理
坐标变换是指在描述同一个空间时,由原来的坐标系变换为另一个坐标系。设原来坐标系中的变量为 X=[x1,x2,…,xn]',新坐标系下的变量为 Y=[y1,y2,…,yn]'。若两组变量关系可以表示为

其中,A称为变换矩阵,其元素称为变换系数,可以取实数或复数,也可以为时间t的函数。要使新变量与原变量间具有单值的对应关系,必须是满秩线性变换。在此情况下,反变换式可写为X=A-1Y,其中A-1是矩阵A的逆矩阵。
2.2 电压、电流和阻抗的坐标变换规律
在三相或两相坐标系中有U=ZI。其中,U和I分别为电机的电压和电流列阵,Z为整个电机的阻抗矩阵。若保证电压和电流具有相同的变换形式,即

如果Z是满秩矩阵,且A是Z的特征相量组成的变换矩阵,则Z'是特征值组成的对角阵。如果保持交流电机定子端点的瞬时功率在变换前后不变,从数学的角度分析即
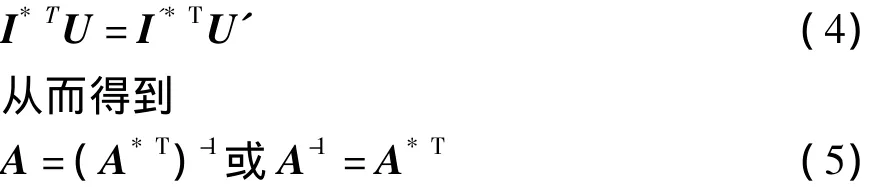
即变换矩阵必须是单式(酉)矩阵,如果A是实数阵,则A-1=AT为正交阵。
3 坐标变换在电力系统中的应用
3.1 Park变换的形式及其选择
Park变换在不同的文献中可能采用不同的符号、不同的参考正方向、不同形式的变换矩阵以及不同的基准值选择方法。从数学上讲,Park变换就是将定子电流、电压和磁链的abc三相分量通过相同的坐标变换矩阵分别变换成dq0三个分量。如果把坐标轴线放在转子上,d轴为直轴,交轴q领先d轴90°,θ为转子直轴与定子a相磁轴间夹角。变换关系统可一写成

式中,θ=ωrt+θ0,ωr是转子的角速度,θ0是t=0 时转子直轴与定子a相磁轴间夹角的初始值;k1到k4可以取非零的各种常数。
电力系统实际应用中要求坐标变换是可逆且线性的。如果从数学规则出发,可以得到无穷多的变换矩阵。但在电力系统实际应用中常选用的坐标变换均具有对应的物理意义:一种是在变换前后保持变量瞬时值的幅值不变,称为恒相幅值变换;另一种是变换前后的瞬时功率不变,称为恒功率变换[5]。
要保持原变量的相幅值和新变量的相幅值相等时,取k1=1,k2=1,k3=1,k4=1/2,一般称为经典Park变换;这种变换后的磁链方程中的互感不可逆,变换前后的电磁功率不守恒[6]。前者一般可以通过适当选择转子电流的基准值予以克服;而电磁功率不守恒的问题则无法改变。
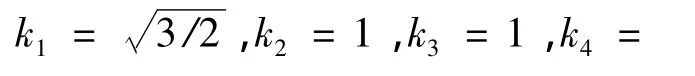
文献[8]指出经典Park变换及其标么系统所导出的系统最贴切地反映了电机的物理特性,且由此产生的等值电路中的电感与电机设计者正常计算的相一致。因此,经典Park变换被电力工业和发电机制造厂家广泛采纳。但是在分析电机的某些问题(如研究电机的机电过渡过程)时,为保证变换后所得前后两类变量所表示的整个系统的总功率是相同的,必须采用恒功率变换。
由于Park变换处理的是三相电流、电压和磁链的瞬时值,因此这种变换更适合于分析暂态过程,如三相短路、自励磁、次同步振荡过程等。但是当发电机计及定子暂态,采用派克方程描写时,网络方程应采用电磁暂态模型与之接口,以便计及暂态电量,这种模型常被用于电磁暂态分析。
3.2 Clarke变换及其应用
Clarke变换是三相静止坐标系和αβ0坐标系之间的变换,设定等值定子α相轴线与a相磁轴重合;β相绕组磁轴越前α相π/2,至于0轴,与其它轴向分量无关,一般不考虑其磁轴位置。其物理意义可理解为原abc三相静止绕组用αβ两相静止绕组和零轴绕组代替,它相当于将三相电机转化为两相同步电机,因此Clark变换又称为相变换:

这种坐标系统与θ=0时的dq0坐标系统相同,其中C可以采用保持原变量的相幅值和新变量的相幅值相等的变换矩阵,或保持恒功率变换的变换矩阵。当无零轴分量时,iα=ia,Clark变换使用起来很方便。经过Clark变换后,对称交流电机的定子和转子的电感矩阵由原来对称循环矩阵变成对角阵,从物理上看,3相变2相系统后,由于α轴和β轴在空间互相垂直,互感为0,而零序又是一个孤立的系统,所以α、β和0三根轴线之间达到解耦[9]。
3.3 两相旋转坐标系之间的变换及其应用
在电力系统的稳定性分析中,系统模型包含了大量的微分方程和发电机模型和网络模型。每个电机的模型是用它自己的随转子而旋转的dq坐标表示的。而网络方程,则是采用一个以同步速旋转的基准参考坐标系表示的(在电机分析中常称为dcqc坐标系,在电力系统分析中称为x、y坐标系)。基准参考坐标的dc轴(x轴)轴常用来作为测量电机转子角的参考轴。因此需要把全部电机的方程也采用基准参考坐标系表示,即需要进行不同转速的两相旋转坐标系间的变换,以构建全系统模型。以电流为例,dcqc分量与dq分量间的关系为
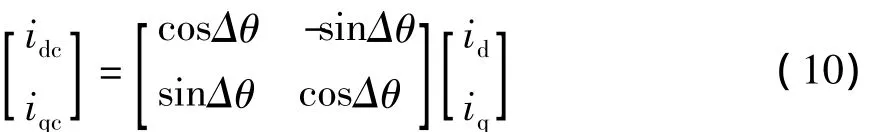
式中,Δθ=θ-θ'即d与dc轴间的夹角。因d轴是以转子转速ω=ω0+Δω 旋转,当 ω=ω0时,Δθ=θ0-θ0',dcqc轴与 dq轴间的差别只是他们初始角 θ0与θ0'的选择不一致带来的。
3.4 对称分量变换及其应用
一般情况下,对于正常运行的电力系统或发生三相短路故障时,其等值电路各相电流电压之间关系解耦,可以用单相电路来研究。当系统发生三相不对称故障时,由于故障电路的三相不对称使得三相电流不平衡,这时就不能用单相电路来研究。可以采用相分量分析,即将整个系统都用三相电路模型来描述,用这种方法分析起来十分复杂。另一种方法就是采用坐标变换的方法,如对称分量变换。
对称分量变换是一种线性变换,它将abc三相电流和电压分解成三组abc三相平衡的电流和电压,分别称为正序、负序、零序电量。对每组三相平衡的电流和电压分别用单相电路来研究。最后再将各组电流叠加,得到三相不平衡电流的每相电流。当元件相分量阻抗矩阵Zabc具有循环对称性质,则经过对称分量变换,Z120将成为对角线矩阵,即意味着三序电量之间解耦。它包含两种含义:第一是对于任意一组序分量,其三相等值电路中三相电量之间解耦,所以每序三相电量可取其中一相来研究。第二是对三相序分量电量中的同一相的序分量也解耦,如正序a相、负序a相和零序a相这三序a相电量解耦,即由三相平衡元件组成的电网用序分量研究时,各序等值电路相互独立。由于故障部分的电路是三相不对称的,所以三序电流流过故障电路时将会是序间有耦合的。这时可以根据短路的类型,建立起故障处的边界条件,用于不对称故障的分析和计算。
4 结语
综合以上分析可见,坐标变换原理简单,但是在电力系统应用时,并不是单纯的数学问题。我们往往要结合电力系统的元件特性或要研究问题的物理性质选择合理的方式灵活的应用。在电力系统分析特别是电机的各种运行状态分析以及矢量变换控制技术中常利用坐标变换来简化问题的数学模型或实现高性能的解耦控制。本文提到各类坐标变换在应用时,需要注意如下问题。
(1)满足要求的变换在实际应用中往往根据变换的实际物理意义进行选取,如经典Park变换采用的就是恒相幅值变换;
(2)一般说来,假定在恒定转速条件下,假如定子及转子的某一方面是对称的,而同时另一方面是不对称的,则较合适的方法是将坐标系统放在不对称的那一边。例如在研究凸极同步发电机突然三相短路时,我们就采用了固定在转子上的dq0坐标系统来进行分析;而研究凸极电机不对称短路问题时,定子和转子都是不对称的,在这种情况下,可采用αβ0坐标系统。Clark变换可建立严格的同步电机模型,因此广泛用于不对称故障暂态过程的分析;
(3)如果进行机电暂态分析,通常采用忽略发电机定子暂态的实用模型,对应的输电线路等元件一般也采用忽略电磁暂态用代数方程描写的准稳态模型。但是当发电机计及定子暂态,采用park方程描写时,网络方程应采用电磁暂态模型,以便计及暂态电量,这种模型常被用于电磁暂态分析;
(4)对称分量变换是相量之间的变换,只能用于暂态过程中某一特定时刻或稳态分析,其它几种坐标变换都可用于暂态全过程分析。当需要计算任意时刻的不对称短路故障电流时,需要借助正序增广网络和三相短路电流运算曲线进行求解。且对称分量变换的电源模型只能近似的以正序网络中某一阻抗后的电势表示,而其它变换可以采用相应的详细的同步发电机模型表示;
(5)Park变换主要用于对称故障分析,其它坐标变换都适用于不对称故障分析;
(6)多机系统的稳定性分析中,也需将电机方程转换为以同步速旋转的基准参考坐标系来表示。
总的来说,数学理论是电力系统分析的有力工具,是工程研究人员或者科研工作者需要掌握的基本技能。但是电力系统中数学理论的应用需要有坚实的专业素养,才能根据实际问题的需要找到正确的数学理论并加以合理的应用。即能够在研究思路的选择上、思考的技巧上或者在思维的方法上,有新的见解、新的发现、新的突破,从而具有一定范围内的首创性和开拓性。
本文的专题教学内容通过坐标变换的思想将电力系统的专业基础课和专业课做了有效的串联,并沟通了工科专业和数学基础之间的关系,希望能够为学生今后的工程实践和理论研究提供有效的分析思路,提高学生分析问题和解决问题能力。
[1]王锡凡主编,现代电力系统分析[M].北京:科学出版社,2003.
[2]王 敏,汪兴强,李生虎,电力系统分析学习的关键知识点[J].电气电子教学学报,2008,30(2):52-53,56.
[3]汤蕴璆,张奕黄,范瑜编著,交流电机动态分析[M].北京:机械工业出版社,2005.
[4]任元陈,贤治,张永立,李国久,保持派克方程精确度的同步发电机实用计算模型[J].华中工学院学报,1983,11(5):115-128
[5]马志云主编,电机瞬态分析[M].北京:中国电力出版社,1998
[6]诸骏伟主编,电力系统分析[M].北京:中国电力出版社,1995
[7]杨顺昌编著,电机的矩阵变换[M].重庆:重庆大学出版社,1988
[8][加]PARBHA KUNDUR著,电力系统稳定与控制[M].北京:中国电力出版社,2001
[9]Chattopadhyay S,Mitra M,Sengupta S.Electric power quality[M].Berlin:Springer Netherlands,2011.

