基于DNA自组装的全错位排列问题模型
唐新玉,殷志祥
(安徽理工大学理学院,安徽 淮南 232001)
自文献[1]利用DNA 计算方法解决了哈密尔顿路径问题以后,越来越多的学者开始关注DNA计算并提出解决图论问题的方法,如0-1 规划问题,图着色问题,最小生成树问题等。
DNA 自组装是依赖分子间非共价键作用力自发的完成由小分子形成较大且复杂的结构。文献[2]、文献[3]首次利用DNA 分子构成了自组装Tile 结构,并利用其中一种瓦片结构建立了多种复杂的算法模型。2000年,文献[4]通过实验给出了自组装DNA 计算模型求解累积异或运算的实现过程和方法。2002年,文献[5]将自组装DNA 计算的基本思想用于求解布尔逻辑表达式并将其实现逻辑电路。2004年,文献[6]利用DX Tile 结构实现了一维元胞自动机,在此基础上分析证明了用DNA Tile 自组装结构实现任何元胞自动机的可行性。Tile 自组装还被用来解决组合优化问题[7-8],2008年,文献[9]在前任的基础上提出了求解可满足性问题的非确定性自组装模型。
全错位排列是组合数学中常见的一类问题,文献[10-11]给出了基于表面、基于芯片以及基于三链的DNA 计算模型,与以往模型相比,本文给出的模型操作更为简单,更易得出可行解。
1 全错位排列问题
全错位排列问题即“装错信封问题”,可用数学语言描述如下:
对于n元集合{1,2,…,n},当满足条件ij≠j(1 ≤j≤n)时,得到的全排列i1,i2,…,in称为全错位排列。
本文以3 元集合{1,2,3} 为例具体说明。即求数字1,2,3 都不在各自的自然位置上的全排列。经分析知,存在3 个原子命题:①数字1 排在第二位,记为u;②数字2 排在第一位,记为v;③数字3排在第一位,记为w。它们的否命题分别为:u'表示数字1 在第三位;v'表示数字2 在第三位;w'表示数字3 在第二位。问题需满足条件:①若数字1在第二位,则数字3 不在第二位;②若数字2 不在第一位,则数字3 不在第一位;③若数字1 在第三位,则数字2 不在第三位。上述问题可以转化为
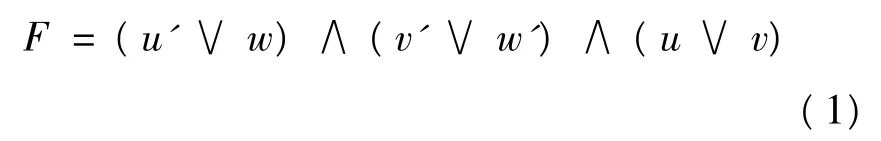
2 操作过程
步骤1
1)给出6 种短的寡聚核苷酸来代表u,v,w和u',v',w'(其中u,v,w对应的寡聚核苷酸取值为1,u',v',w'对应的寡聚核苷酸取值为0),并把它们的补链记为和(其中第一段不参加反应,第二段为u,v,w和u',v',w'的前四个碱基的补,第三段为u,v,w和u',v',w'的后四个碱基的补)(见表1)。由此,和的完全补链和也可以确定。

表1 所有变量和其补链的编码
2)合成所需的8 种DNA 链放入数据池中,然后进行纯化和PCR 扩增(见图1a)
步骤2
首先判断子句(u'∨w),往数据池中加入足量的u',w的补链,数据池中含有u',w的DNA序列将与补链发生杂交反应形成发夹结构(见图1b),与此同时,使式(1)中子句(u'∨w)为假的组合不形成发夹结构,通过凝胶电泳,将不符合条件的DNA 链分离出去,剩余的DNA 链即为使(u'∨w)为真的链。
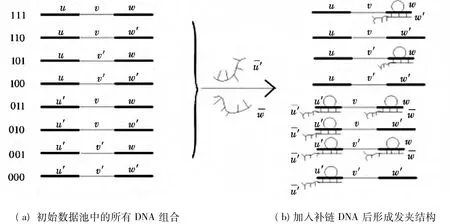
图1 初始DNA 链与补链杂交图
步骤3
步骤4
重复步骤2、步骤3,检查式(1)中的剩余子句,提出F中所有不满足条件的DNA 链后,最后剩余的DNA 链满足F式的所有子句,也就得出了全错位排列的排列顺序。通过测序知为101 和010,所以231 和312 即为所求的全错位排列。

图2 发夹结构打开过程
3 结论
通过把全错位排列问题转化为可满足问题,利用自组装的方法最终得到三元全错位问题的具体排列顺序。这种方法在实现过程中只用到凝胶电泳操作,在一定的程度上减少了因生物操作过多而引起的各种实验误差,便于计算三元以上的全错位排列问题。
[1]LEONARD ADLEMAN.Molecular computation of solution to combinatorial problems[J].Science,1994,Z66(11):1 021-1 024.
[2]SEEMAN N C.DNA nanotechnology:novel DNA constructions[J].Annual Review of Biophysics and Biomolecular Struture,1998,27:225-248.
[3]MAO C,SUN W,SEEMAN N C.Designed two dimensional DNA Holliday junction arrays visualized by atomic force microscopy[J].Journal of the American Chemical Society,1999,121(23):5 437-5 443.
[4]MAO C,LABEAN T H,RIEF J H,et al.Logical computation using algorithmic self-assembly of DNA tri-crosser molecules[J].Nature,2000,407(6803):493-496.
[5]CARBONE A,SEEMAN N C.Circuits and programmable self-assembling DNA[J].Academy of Sciences of the United States of America,2002,99(20):12 577-12 582.
[6]ROTHEMUND P W K,PAPADAKIS N,WINFREE E.Algorithmic self-assembly of DNA Sierpinski triangles[J].PloS Biology,2004,2(12):2 041-2 053.
[7]MICHAIL G L,LABEAN T H.2D DNA self-assembly for satisfiability[J].DIMACS Series in Discrete Mathematics and Theoretical Computer Science,1999,44:139-152.
[8]BRUN Y.Solving NP- complete problems in the tile assembly model[J].Theoretical Computer Science,2008,395(1):31-36.
[9]BRUN Y.Solving satisfiability in the tile assembly model with a constant- size tile set[J].Journal of Algorithms,2008,63(4):155-156.
[10]孙侠,殷志祥,李勇,等.全错位排列问题的基于芯片的DNA 计算模型[J].大学数学,2010,26(2):79-82.
[11]孙侠,殷志祥,赵前进,等.基于三链DNA 结构的全错位排列问题算法[J].滁州学院学报,2012,2(14):18-20.
[12]RAVINDERJIT S BRAICH,NICKOLAS CHELYAPOV,CLIFF JOHNSON,et a1.Solution of a 20-variable 3- SAT problem On a DNA computer[J].Science,2002,296(5567):499-502.
[13]XU JIN,QIANG XIAO- LI,FANG GANG,ct a1.A DNA computer model for solving vertex coloring problem[J].Chinese Science Bulletin,2006,51(20):2 541-2 549.
[14]方刚,张社民,朱岩,等.基于三链核酸的DNA 计算[J].生物信息学,2009,7(3):181-185.
[15]孙侠,殷志祥,张家秀.全错位排列问题的基于表面的DNA 计算模型[J].生物数学学报,2009,24(3):513-517.
[16]宋勃生,殷志祥,甄诚,等.DNA 自组装的可满足性问题模型[J].小型微型计算机系统,2011,9(32):1 872-1 875.

