基于N－最短路径的中文分词技术研究

吴晓倩，胡学钢

(1.合肥工业大学计算机与信息学院，安徽 合肥 230009;2.安徽医学高等专科学校公共卫生与卫生管理系，安徽合肥 230061)

中文分词是信息处理的基础，中文信息是由句子组成的，句子又是由词组成的，词是最小的能够独立活动的有意义的语言成分，但汉语是以字为基本的书写单位，词语之间没有明显的区分标记。如何在这些由连续的文字组成的语句中把一个具有独立意义的词汇切分出来就是一个很有挑战的问题。

1 现有的分词算法及难点

1.1 现有的分词算法

现有的分词算法分为三大类:基于词典的分词方法、基于统计的分词方法和基于理解的分词方法。

1)基于词典的分词。这种方法要事先有一个词典，词典尽量囊括所有的词汇，然后将待切分的句子按照一定的规则扫描，与词典中的词条进行匹配，如果匹配成功，则将该词条切分出来，否则进行其他处理。按照扫描方向和不同长度优先匹配的情况，基于字符串匹配分词方法又分为正向最大匹配法、逆向最大匹配法、最少切分法和双向最大匹配法四种。大多数的系统是以该方法为主来实现的。

文献［1］提出了一种改进的正向最大匹配算法，改进后的算法采用类似TRIE 索引树的逐字匹配算法，消除了正向最大匹配算法的切分盲点，同时，避免二分查找，提高分词效率;文献［2］提出了一种基于双词典机制的中文分词方法;文献［3］提出了全二分最大匹配快速分词算法，分词词典存放在内存，在查找时，不用进行I/O 操作，减少了匹配次数。

2)基于统计的分词。此方法认为，中文中的词组是固定的，所以在文章中，相邻的字出现的频率越高，就有可能是一个词，用字与字之间相邻出现的概率反映成词的可信度，通过统计文本中各个字的组合的频度，计算它们之间的互现信息，从而判断汉字之间的紧密程度，当紧密程度达到一个阈值，就认为可能构成一个汉字。

3)基于理解的分词。基于理解的分词结合文本的句法、语法分析和语义分析，通过对上下文内容所提供信息的分析对词进行界定，通常由总控部分、分词子系统和句法语义子系统三部分组成。但是由于汉语言的复杂性，难以将各种语言知识组织成机器可以直接读取的形式。因此，这种方法并没有普及应用，还处于试验阶段。

4)难点。目前虽有中科院、微软等研究机构推出的一些实验系统(如CSW、WB2000 等);但分词效果仍不尽如人意。中文分词的难点主要体现在歧义现象、对未定义词的识别和词性的多重性几个方面。

1.2 N-最短路径算法简介

N－最短路径的分词算法的基本思想是根据词典，顺序匹配出在中文字串中所有可能的出现的词的集合，所有词语作为一个节点构造成为一个有向无环图。在该图中起点到终点的所有路径中，求出每个节点的所有到源节点的路径值，每个路径值对应一个路径集合，作为相应的分词结果集。

设待分字串S= c1c2…cn，其中ci=(i=1，2，…，n)为单个的字，n为串的长度，n≥1.建立一个结点数为n +1 的切分有向无环图G，各结点编号依次为V0，V1，V2，…，Vn。

通过以下两种方法建立G所有可能的词边。

1)相邻结点Vk－1，Vk之间建立有向边＜Vk－1，Vk ＞，边的长度值为Lk，边对应的词默认为ck(k=1，2，…，n)。

2)若w= cici+1…cj是一个词，则结点Vi－1，Vj之间建立有向边＜Vi－1，Vj ＞，边的长度值为Lw，边对应的词为w(0＜i ＜j≤n)。

这样待分字串S中包含的所有词与切分有向无环图G中的边一一对应(见图1)。

这样，对句子的最短切分问题就转化为找出图1 中从开始节点到结束节点的最短路径问题［4］。

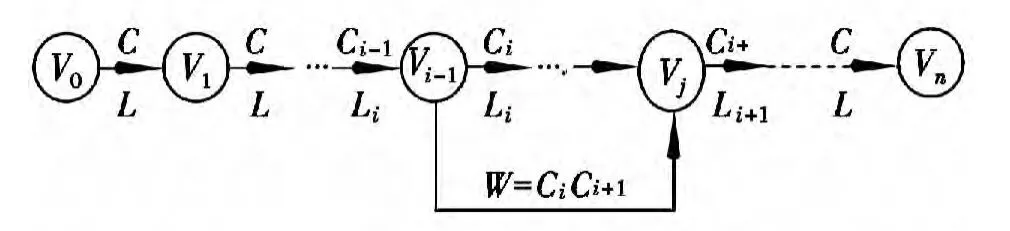
图1 分词路径图

基于N－最短路径的分词算法，需要计算有向图中从起点到终点的所有路径值，分词效率低。

2 改进的N－最短路径算法

正确、快速的中文分词算法，会提高排歧、未登录词的识别、词性标注的最终效果，提高中文词语分析质量。本文在对多种算法的优劣进行分析之后，在N－最短路径算法的基础上，采用动态算法在旧的最短路径的基础上，删除某条弧，并寻找替换的弧来寻找下一条可选的最短路径，即通过在有向图中增加附加节点和相应的弧来实现，减少了搜索路径范围，计算速度快，分词效率高。

2.1 对算法的改进

将动态删除算法［5－8］与最短路径算法结合起来，可以改进分词的效率。动态删除算法的原理是建立一个最短路径树更新队列，将所有将被删除节点的子孙节点保存到该队列;从原最短路径树中删除需要被删除的节点和其所有子孙节点;从队列中选取与根节点距离最短的节点进行更新，已更新节点不再被插入队列，从而减少节点更新次数。

改进后的算法描述如下:

1)根据N－最短路径算法构造分词路径图1所示的图G(E，R)，计算从开始节点V0到结束节点Vn的最短路径为Lj，j=1。

2)IF(j＜最短路径数)and(候选路径存在)Then 更新当前路径L为Lj。否则，程序结束。

3)删除当前路径中第一个节点开始的入度大于1 的第一个节点，记为Hm，如果被删除节点的子孙节点不在集合E中，则转4);否则从G中删除Hm节点和其所有的子孙节点，转5)。

4)计算从开始节点V0到Hm的最短路径，记最短路径的结束节点为H'm。

5)对于从Hm之后的所有节点，重复过程3)。

6)更新当前路径树，求得从节点V0到所有结点H'm的最短路径，j=j+1，转2)继续。

2.2 算法示例

以“他说的确实有用”为例，假设N=3，看一下求解的过程。图2 是构造的有向图。

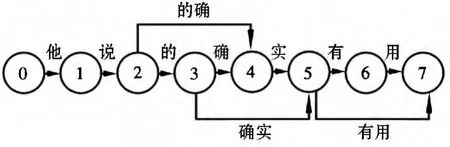
图2 初始构造的有向图

利用上述算法计算最短路径，求其第j条最短路径，算法的执行过程中，图1 的变化如图3～图6所示。其中粗线表示当前状态下的最短路径，虚线圈删除某一节点更新后生成的节点。

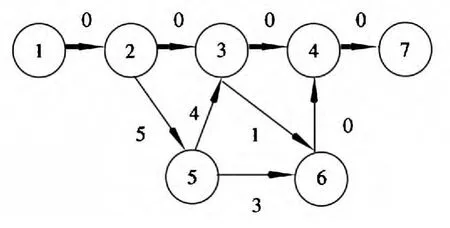
图3 j=1 时的最短路径

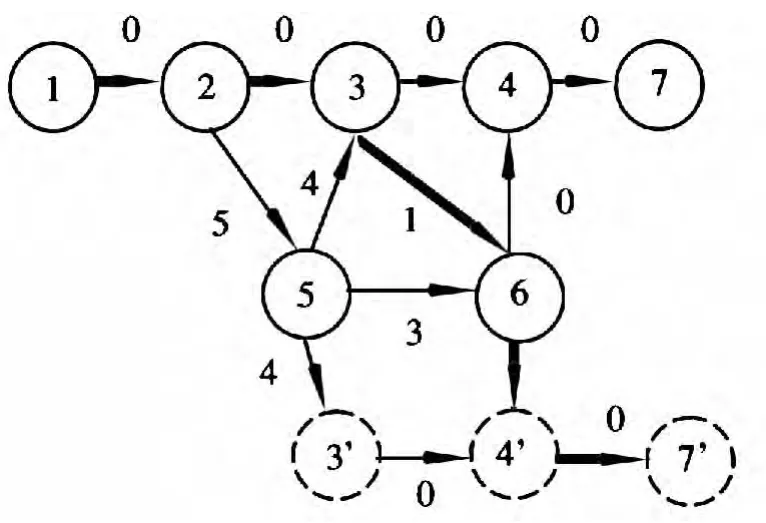
图4 j=2 时的最短路径

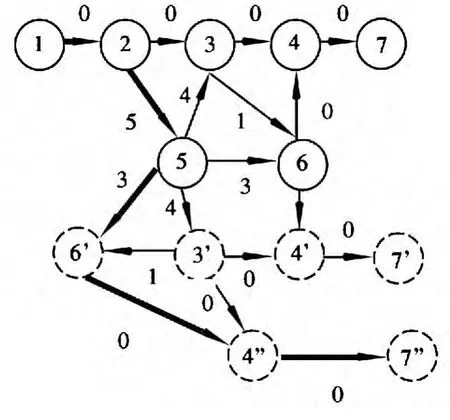
图5 j=3 时的最短路径

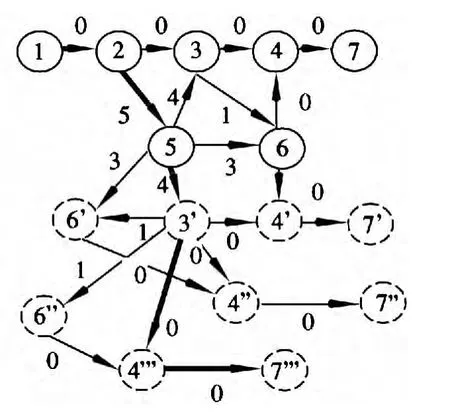
图6 j=4 时的最短路径

在算法求解过程中，还可以继续对j值增加，继续寻找最优路径，寻找方法同上，由于篇幅有限，不再进行描述。实际上，N－最短路径算法的路径搜索过程，就是在最短路径和最大路径的折中方法。在求解的过程中，通过保留前j个最优路径，j的取值应该选择一个适中的值，取值过大会影响搜索的速度，取值过小，又会影响分词的准确性。

3 实验与结果分析

基于Java 开发平台，对上述的分词算法进行了实现，针对从网易、新浪、腾讯等网站的监测内容进行对比实验，测试的文本总量为300 篇。实验采用统计的方法，对不同的K值，首先统计出每一文章的句子字节总数SUM，根据算法系统的运行时间和结果，统计每一篇文章分词所用时间T，从分词结果中计算出分词正确的词的数量FSUM，分词的正确率=(正确粗分的句子数量FSUM/句子总数SUM)* 100%;分词的速度=(句子字节总数SUM/分词所用时间T)。通过多次测试实验，并参照同行公布的试验数据，本文改进的算法与其他算法的性能对比如表1所示。

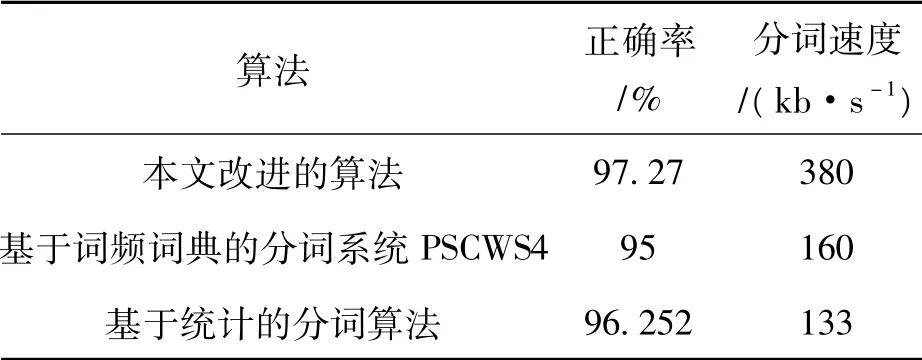
表1 业界公布的数据与本文的分词系统对比

本文的数据来源于实验数据，由于测试结果与系统的实际运行环境有关，在实际应用时，分词速度可能与本实验有一定的误差。

4 总结

本文对N－最短路径算法进行了改进，将动态删除算法与最短路径算法结合起来，可以改进分词的效率。通过对从网站上监测的内容进行分词实验测试，将测试结果与业务公布的算法的效率进行比较，结果表明此方法的分词速度得到了一定的改善。

［1］叶继平，张桂珠.中文分词词典结构的研究与改进［J］.计算机工程与应用，2012，48(23):139－142.

［2］李玲.基于双词典机制的中文分词系统设计［J］.机械工程与自动化，2013，176(1):17－19.

［3］李振星，徐泽平，唐卫清，等.全二分最大快速分词算法［J］.计算机工程与应用，2002，38(11):106－109.

［4］苗夺谦.中文文本信息处理的原理与应用［M］.北京清华大学出版社，2008:26.

［5］粱德恒，姚国样，官全龙.基于路由最短路径树的动态多节点删除算法［J］.计算机工程，2011，37(5):121－123.

［6］刘代波，侯孟书，武泽旭，等.一种高效的最短路径树动态更新算法［J］.计算机科学，2011，38(7):96－99.

［7］韩月阳，邓世昆，贾时银，等.基于字分类的中文分词的研究［J］.计算机技术与发展，2011，21(7):29－31.

［8］孙知信，高艳娟，王文鼐.更新最短路径树的完全动态算法［J］.吉林大学学报:工学版，2007，37(4):860－864.