基于人工鱼群遗传算法的DNA编码优化

胡 娟，李 冬，张丽丽

(1.淮南职业技术学院基础部，安徽 淮南 232001;2.淮南工业学校电子组，安徽 淮南 232001;3.安徽理工大学理学院，安徽 淮南 232001)

1994年，当文献［1］用DNA 计算成功地解决了有向Hamilton 路问题，人类已经进入了借助DNA 分子通过生化反应来进行计算的崭新时代。从此越来越多的学者用DNA 计算模型解决了许多NP 完全问题，然而早期DNA 计算中所用的序列都需要在设定编码长度的基础上随机产生，这就会导致生物化学反应不可控制性。因此寻找高质量DNA 序列及合适的DNA 序列库变得尤为重要。通常为了满足DNA 序列可靠性的要求，就会利用约束条件来筛选序列，决定序列编码的约束条件主要有Gibb 自由能增量约束、解链温度约束Tm、H－measure 约束、生物酶和DNA 分子的生物特异性等，要想找到好的编码就需要充分考虑这些约束条件。

遗传算法(Genetic Algorithm，GA)是20 世纪70年代初文献［2］16首先提出来的。它常用来处理很复杂的非线性问题，具有非常好的鲁棒性。但它最大的缺点就是进化过程盲目性，常会陷入局部极值。尤其在编码问题中，当约束条件较多时，它有可能会搜索不到符合要求的编码。而全局人工鱼群算法是模仿鱼群觅食的一种算法，算法简单，又有避免陷入局部极值的良好能力。

本文在深入研究传统遗传算法的基础上，为了克服其盲目搜索的缺点，提高进化效率，给出了一种基于遗传算法和全局人工鱼群算法的混合优化算法(GAFSA/GA)，用于DNA 的编码问题，经实验结果表明，所述算法比遗传算法产生的DNA 编码序列质量更加稳定可靠。

1 DNA 编码序列设计及约束项分析

1.1 DNA 编码问题

DNA 计算中的编码问题一般都描述为:设由四个字母组成的集合∑={A，T，C，G}，若DNA分子长度为n，其编码集合为S，很明显有|S|=4n，求C⊆S使∀xi，xj∈C，τ(xi，xj)≥k，其中τ 为评价标准，k∈Z+。然而τ 越严格，可供选择的编码数|C|就会越小。编码问题，主要是编码质量和数量问题。因为编码质量越高，可靠性就会越好;而编码数量越大，就会扩大应用范围。然而，在现实中，他们是相互矛盾的。这就希望在保证质量的前提下能最大限度的得到编码集合。

1.2 约束项及评价函数

影响DNA 计算的因素［3－7］有很多，结合众多约束条件，给出本文的DNA 编码的约束条件。

1)H－measure 约束。H－measure 是一种通过移位比较两个DNA 序列汉明距离的最小值而获得的有效约束，移位后的互补碱基对的数目可以有效防止杂交，定义公式如下:

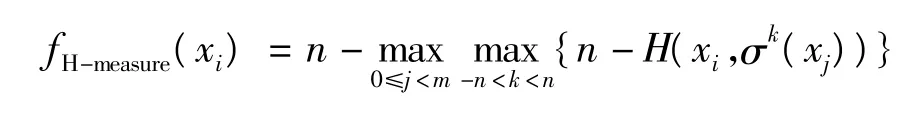
式中:σk(xj)为xj序列经移位k位后的序列Hamming 约束。

2)Similarity 约束。相似度是计算2 个正相序列移位后的序列的相同碱基对的数目，来度量序列在集合中的差异性。

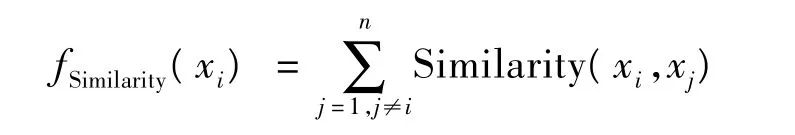
3)Continuity 约束。如果DNA 序列中某一字母连续重复出现，那么结构将会变得不稳定。

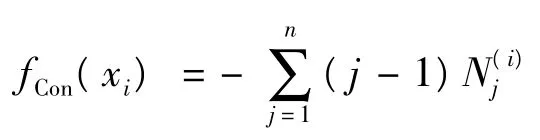
4)Hairpin 约束。发夹结构会引起DNA 序列的自杂交，一般情况下应加以限制。式中:r为形成发夹的最小的环长度;pinlen为形成发夹茎所应有的最小长度。

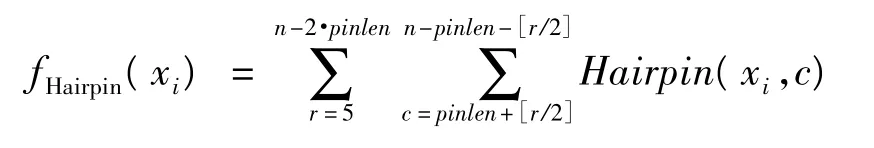
5)GC Content 约束。

fGC(xi)=－|GC(xi)－ GC(xi)defined|

式中:GC(xi)为xi序列中字母G，C 在序列中的比例;GC(xi)defined为所指定的GC 含量。

6)Tm约束。温度是实现DNA 计算的一个重要因素。在这里采用最近邻模型近似表达式:

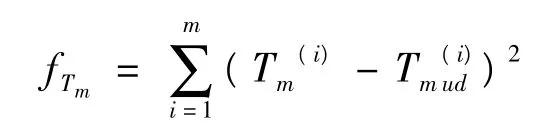
1.3 适应度函数

本文定义的优化问题其实是最大值问题，因此采用加权平均值法来处理每个DNA 个体各约束的评估函数。

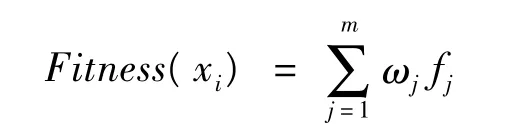
式中:m为约束项个数;ωj为各个约束项fj的权重。

2 人工鱼群遗传算法

2.1 基本遗传算法

遗传算法是模拟生物进化过程中适者生存规则，并将其与种群内部染色体的随机信息进行交换，是一种很好的局部优化搜索方法［2］141。它的主要思想是:随机生成DNA 序列;计算DNA 序列的适应度函数值，满足约束条件;利用遗传算子生成满足约束条件的新的DNA 序列，从而获得DNA 序列的集合(见图1)。

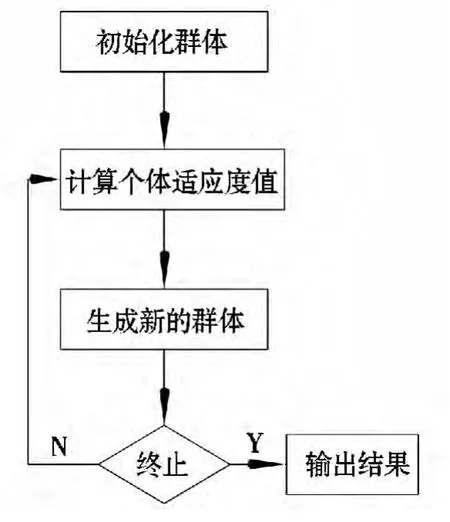
图1 算法流程图

2.2 人工鱼群算法(GAFSA)

人工鱼群算法就是模拟鱼群的觅食，聚首及追尾行为而生成的全局优化算法。通过观察鱼觅食会发现在一片水域中，鱼最多的地方就是食物最多的地方，鱼有自行或尾随其他鱼找到食物最多的地方特点。人工鱼群算法就是根据鱼群的这一特点，来构造人工鱼群来模仿鱼群行为，从而实现寻优。

1)确定鱼群规模N，随机产生N个人工鱼个体，组成初始群体，同时设置相关参数;

2)计算初始鱼群的个体适应函数值，并将最优人工鱼状态记录到公告板;

3)个体通过觅食行为，聚首行为，追尾行为［8］生成新的鱼群;

4)选最优个体与公告板进行比较，若比公告板优，则以自身状态更新公告板;

5)根据文献［8］对视野和步长进行调整;

6)判断是否满足终止条件，若满足，则输出公告板记录，算法终止;若不满足，则执行步骤3。

2.3 人工鱼群遗传算法(GAFSA/GA)

该算法是以基本遗传算法为基础，将人工鱼群算法作为遗传算法的一个重要算子，具体步骤如下:

1)设定相关参数，并产生初始种群;

2)计算个体的适应度函数值，按照适应度函数值进行排序;

3)判断是否满足目标，若满足，输出结果，结束进程;否则进行下一步;

4)更新个体种群，根据适应度函数值的确定一部分个体直接进入下一代种群，剩余个体通过GAFSA 算法优化过后进入下一代种群;

5)对下代种群执行遗传算法的复制、交叉和变异等操作，转步骤2。

流程图如图2所示。

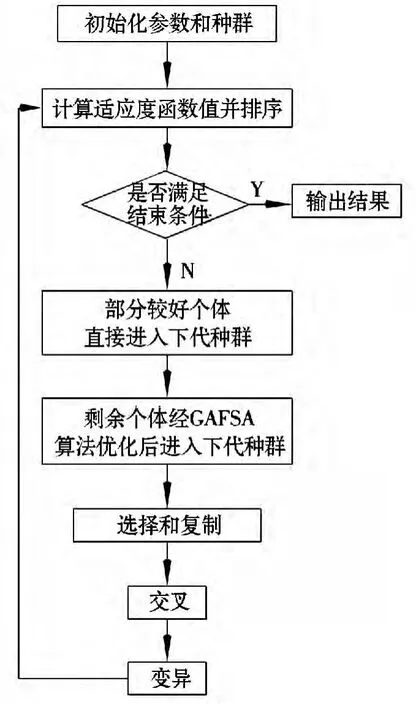
图2 算法流程图

3 算法仿真结果及分析

3.1 与遗传算法的实验比较

用全局人工鱼群遗传算法产生的DNA 序列与文献［9］的遗传算法的编码序列进行了比较，并给出了好的有向哈密尔顿路问题的DNA 序列。比较结果如表1 和图3所示。

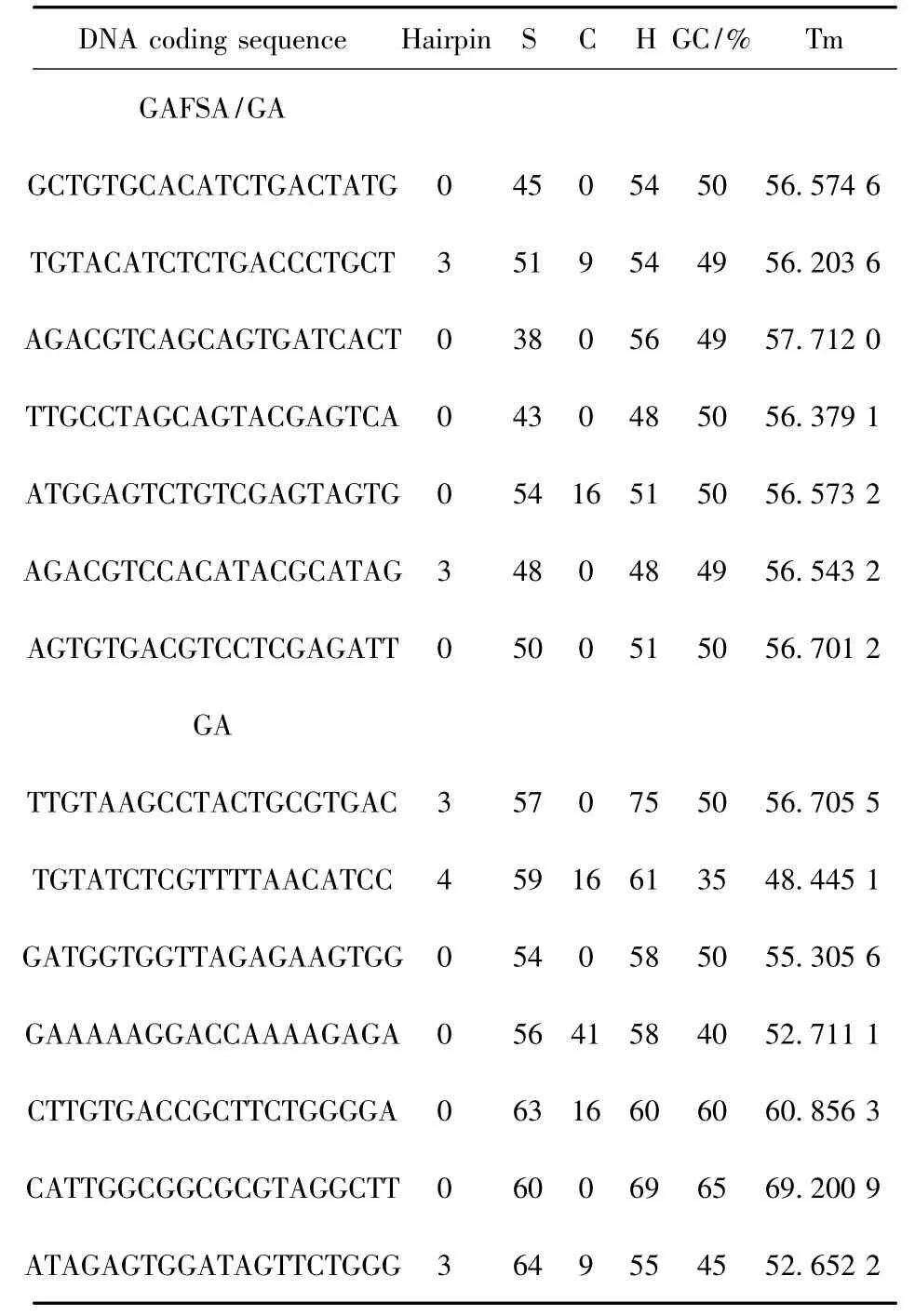
表1 本文算法和GA 序列比较

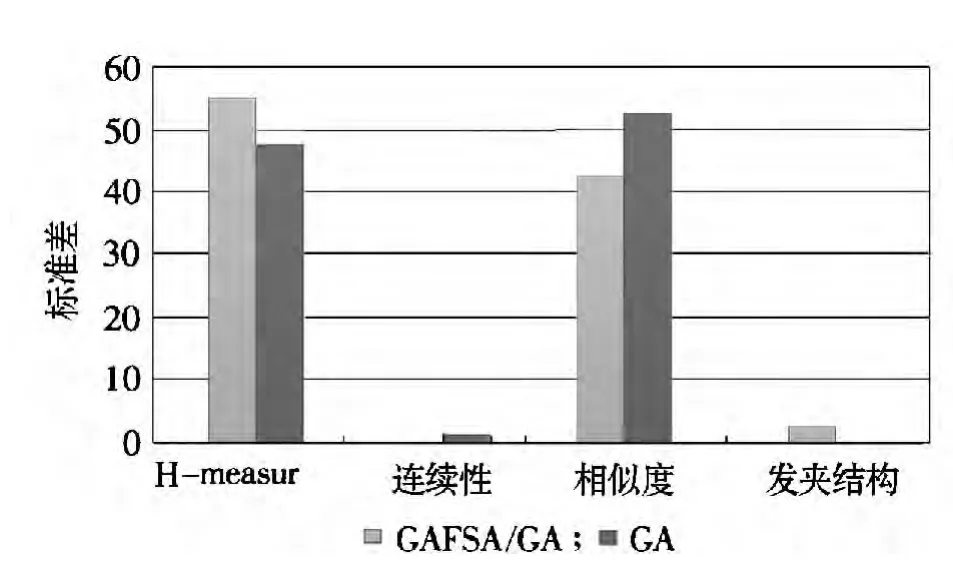
图3 GAFSA/GA 与遗传算法的比对结果

从图3 可以看出，GAFSA/GA 算法生成的DNA 编码序列在Hairpin、GC 含量方面比GA 算法生成的DNA 编码序列更优，并且可以看出GAFSA/GA 生成的序列解链温度变化更小，这意味着GAFSA/GA 算法具有较低的不完全匹配双链产生的概率。同时GAFSA/GA 算法大大降低了计算的难度，在解决DNA 编码问题方面效果很好，而且依靠群体人工鱼并行计算，其收敛速度较快，如(见图4)横轴为进化代数;竖轴为每代群体经排序后最差个体的适应度值。从图4 中可以看出，算法具有较好的收敛性。

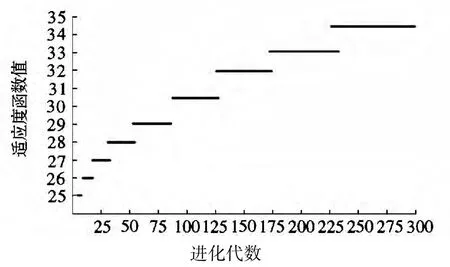
图4 GAFSA/GA 算法的进化收敛图

3.2 与遗传粒子群算法的实验比较

虽然文献［10］遗传粒子群算法(GA/PSO)与GAFSA/GA 选择的约束条件不同，但鉴于实验结果的比对应建立在相同约束条件的基础上进行，采用GAFSA/GA 的评价方法进行实验比对。比较结果如表2 和图5所示。

从表2 和图5 可以看出，GAFSA/GA 算法生成的DNA 编码序列在解链温度、发夹结构等约束方面优于遗传粒子群算法生成的DNA 编码序列。

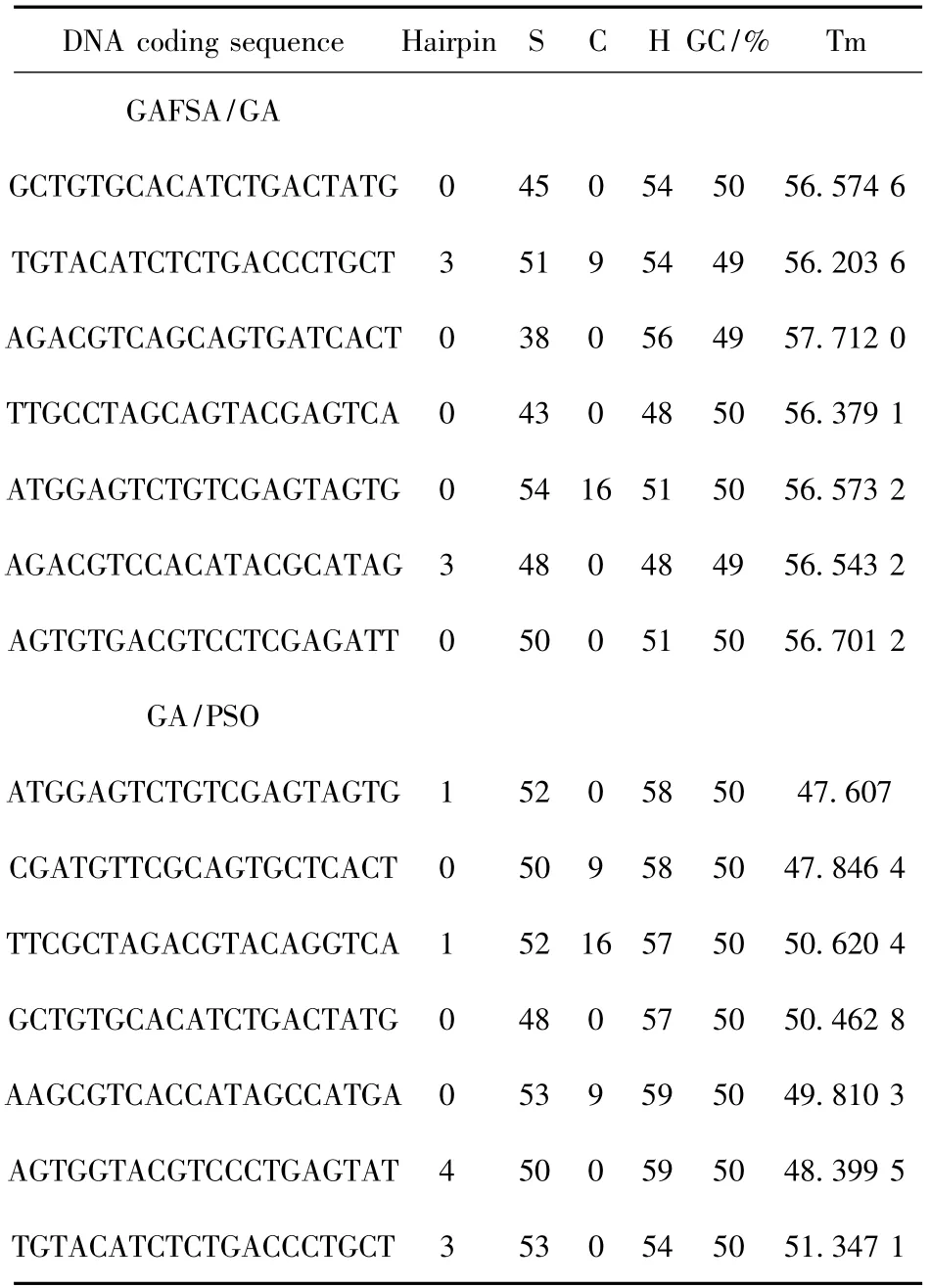
表2 本文算法和GA/PSO 序列比较

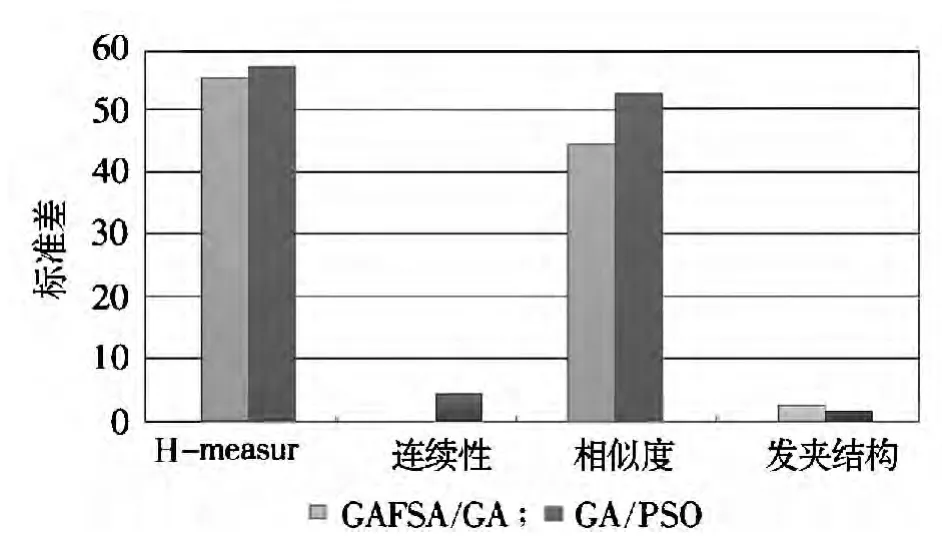
图5 GASFA/GA 与遗传粒子群算法的比对结果

4 结论

从DNA 编码的多个约束条件选取合适的约束，提出了GAFSA/GA 算法对DNA 计算中的编码序列实现了优化，产生了很好的DNA 序列，验证了该算法的可行性和有效性。

［1］ADLEMAN L M.Molecular computation of solution to combinatorial problems［J］.Science，1994，66(11):1 021－1 024.

［2］HOLLAND J H.Adaptation in natural and artificial systems［M］.AnnArbor:University of Michigan Press，1975:1－153.

［3］DEATON R，GARZON M.The Rmodynamic Constraints on DNA－based Computing［C］// Computing with Bio Molecues:Theory and Expirements.ed.G.Paun，Springer－Verlag:Singapore，1998:138－152.

［4］DEATON R，FRANCESCHETI D R，GARZON M，et al.Information transfer through hybridyzation reaction in DNA based computing［C］//Proceedings of the Second Annual Conference，1997，July 13－16，Stanford University，.Morgan Kaufmann，San Francisco:463－471.

［5］DEATON R.A DNA Based Implementation of an Evolutionary Computation［C］// Proceedings IEEE Conference on Evolutionary Computation.Indianapolis，1997:267－271.

［6］MARATHE A.On combinatorial DNA word design［J］.DIMACS Series in Discrete Mathematics and Theoretical Computer Science，1999，44:75－88.

［7］ROSE J A.The Fidelity of DNA computation［D］.Ph.D thesis，The University of Memphis，1999:11.

［8］付媛媛，张大方，向旭宇.基于人工鱼群的DNA 编码序列组合优化算法研究［J］.湖南城市学院学报:自然科学版，2011，20(2):55－56.

［9］ARITA M，NISHIKAWA A，HAGIVA M，et al.Improving sequencedesign for DNA computing［C］// In Proceedings of the Genetic andEvolutionary Computation Conference(GECCO－2000)，2000:875－882.

［10］CUI G Z，NIU Y Y，WANG Y F，et al.A new approach based onPSO algorithm to findgood computational encoding sequences［J］.Progress in Natural Science，2007，17(6):712－716.

［11］Feldkamp U，Raube H，Banzhaf W.Software tools for DNA sequence design［J］.Genetic Programming and Evolvable Machines，2003，4(2):153－171.

［12］张凯，肖建华.基于汉明距离的DNA 编码约束研究［J］.计算机工程与应用，2008，44(14):24－26.

［13］XIAO J H，JIN X，CHEN Z H，et al.A hybrid quantum chaotic swarm evolutionary algorithm or DNA encoding［J］.Computers＆ Mathematics with Applications，2009，57(11/12):1 949－1 958.

［14］CUI GUANGZHAO，LI XIAO GUANG，ZHANG XUN CAI，et al.The Optimization of DNA Encodings Based on Modif ied PSO/GA Algorithm［J］.CHINESE JOU RNAL OF OMPUT ERSVol，2010，33(2):312－313.