人工冻土单轴抗压强度灰色理论预测

牛连僧，姚兆明，2，3，亓燕秋

(1.安徽理工大学土木建筑学院，安徽 淮南 232001;2.安徽理工大学冻土力学研究所，安徽 淮南 232001;3.中煤矿山建设集团有限责任公司，安徽 合肥 230000;4.中煤矿山建设集团有限公司淮南冻结处，安徽 淮南 232001)

冻土的强度一直是冻土力学研究和工程设计、施工所关注的研究课题。冻土是由土矿物颗粒、胶结冰、未冻水、水汽及气所组成的典型的非均匀多相材料，由于各相之间的相互作用，导致冻土表现出的力学性能非常复杂［1］。冻土的单轴抗压强度是有限、离散的，在研究参数的影响因子时，一些重塑土样也无法准确制作，这就需要在已有资料的基础上进行统计分析，建立相应的数学模型，对未知样本进行判断，并对未来趋势作出预测。

预测是根据已有的实际数据资料，应用现代的科学理论和方法，以及丰富的经验和和敏锐的判断力，去探索某事物今后的发展趋势，并作出估计和分析，以指导未来的行动的方向，减少未来事物的不确定性，基于灰色系统理论的动态预测模型，称为灰色预测，其中应用最广泛的是GM(1，1)序列预测模型，由于其所需样本数量少，计算简便等优点已被广泛应用于军事、农业、经济、煤炭工业等各个领域。为使GM(1，1)预测模型更好的服务于社会的生产实践，许多专家学者进行了大量的研究工作，并取得了丰硕的成果。

预测的核心问题是预测方法，或者说预测的数学模型建立。目前，适合中长期预测的方法有回归模型法、弹性系数法、人工神经网络法和灰色模型预测法等。灰色模型自创立以来已经得到很大程度上的改善，目前已经建立了多种初始值和背景值的优化方法。但是原有优化方法仍然存在需要加以改进的地方。

文献［2］在基坑边形预测的灰色二次优化模型中，采用对初始值修正的最小二乘法;对时间响应参数添加修正的解决近似指数的序列改进GM(1，1)模型;对基坑变形直接建模的二次优化的GM(1，1)模型，结果显示再次优化模型有较高的精度。文献［3］在基于GM(1，1)改进模型的建筑物沉降预测中，提出了一种同时优化背景值和初始条件的GM(1，1)改进模型，并将其应用于对建筑物的沉降变形进行定量分析与即时预报，改进的模型在精度上有了显著的提高。

文献［4］通过BP 神经网络法、回归分析法、灰色预测法等对冻土强度进行预测，得出BP 神经网络法预测的结果是可靠的。文献［5］运用神经网络的声波法预测冻土的抗拉、抗压强度，把神经网络预测值与回归方程计算值对比，得出前者优于非线性回归方程计算的结果。文献［6］运用遗传算法与支持向量机相结合的方法对人工冻土单轴抗压强度进行预测，并把Sigmoid 核函数、高斯径向基核函数、多项式核函数的预测结果进行比较，结果表明，多项式函数的遗传支持向量机预测的结果较为可靠。以上文献中对改进的灰色理论在冻土中研究较少，基于此提出了冻土单轴抗压强度的改进灰色理论预测模型。

在已有实测数据的基础上，应用灰色理论对人工冻土单轴抗压强度进行预测，针对传统的灰色模型预测精度不高的情况;增加原始序列的光滑度，将传统模型的白化方程的时间响应式进行改进;验证了改进的模型预测精度明显优于传统模型的精度，为人工冻土单轴抗压强度试验提供了可靠的理论保证。

1 灰色理论

灰色预测模型是灰色系统理论的重要组成部分，灰色系统模型GM(m，n)是以灰色模块概念为基础，以微分拟合为核心建模方法，模型参数中的m为模型微分方程阶数，n为参与建模的序列个数，微分方程的阶数越大，计算越复杂，而精度提高则不明显，因此，通常采用GM(1，1)作为预测模型。

GM(1，1)模型的步骤如下，根据最小二乘法原理，设原始序列［6－10］

将序列进行累加生成AGO(Accumulating Genaration Operator)的递增序列为

如果x(1)序列变化过程为指数曲线，则可建立微分方程为

式中:a为发展系数，反映系统发展趋势;b为灰作用量反映数据的变化关系。

z(1)(k)序列，称为白化背景序列。转化得到差分方程组为

用最小二乘法可得方程组的解为

构造向量(a，b)称为一级数包，记作P1(a，b)的构成成分构成二级数包C，D，E，F称为GM(1，1)二级数包，记作P2(C，D，E，F)，令

从而可求得X(1)序列，再将其累减生成:

利用灰色理论进行建模时，随着时间的推移，新的数据不断加入到原始数据集中，使得原始数据越来越大，数据处理计算量增大，采用等维建模思想，即当增加一个新的信息时，将其加入原始序列中，同时可以认为最老的信息从一定程度上不能反映模型信息而将其舍去，从而保证序列的维数不变，建立新的序列的灰色模型，建模输出及预测误差将在结论中给出。

2 GM(1，1)模型的改进

传统的灰色GM(1，1)模型在短期预测精确度较高，但中长期预测效果并不好，有可能出现预测值偏大的结果，因此出现了各种改进的模型如:新陈代谢GM(1，1)模型［11］、GM(1，1)残差模型［12］，为增加原始序列的光滑度，在确定发展系数a和灰作用量b后，将传统模型的白化方程的时间响应式(5)做下面改进为

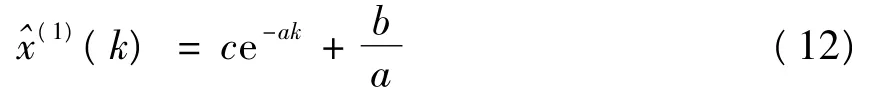
还原值为

式中:c为待求参数。

按照x(0)(k)与模型的拟合值之差平方和最小的原则构建函数F(c)为

令F'(c)=0，可得

将c代入式(11)得

3 灰色模型检验

灰色模型能否适用于人工冻土单轴强度的预测，还需进行必要的数理统计检验，其检验方法一般有残差检验、关联度检验和后验差检验三种。所谓残差检验是对实测值预测值之间的误差进行的一种逐点检验的方法，通过各点的相对残差值，可以计算出预测模型的精度值P，而后验查检验法是根据后验差比值C和小误差概率P0两个参数对所建立的模型划分精度等级(见表1)，若精度达到了“良好”或以上指标则可利用灰色理论对后期数值进行预测。

表1 精度检验等级

设x1为实际值，x2为模型值，y为残值，残差为

相对残差为

平均残差为

著作权又名版权，它是指文学作品、艺术作品的首创作者，对其作品享有的所有权和财产权。因此，作品本身是作者享有权利的根本依据，作品是作者智慧的结晶，凝聚了作者的心血。

精度为

残差的均为

残差数列的均方差为

实测值数列均值为

实测值数列均方差为后验差检验指标:后验差比值c= s

s12，小误差

概率

分别采取残差检验和后验差两种方法对所建立的模型进行检验。

4 灰色模型预测

对淮南某煤矿的人工冻土单轴抗压强度试验在自行研制的WDT－100 冻土性能试验机上进行，试验机由低温箱、自动加载系统、数据采集仪等组成;试验装置最大加载能力为10 吨，精度为0.01。试验荷载和试验数据全部由计算机根据设定好的参数自动控制和采集。试验分别对1～10 土层冻土试样进行了3 个温度水平(－ 5 ℃，－ 10 ℃，－15 ℃)下的单轴抗压强度试验，试验结果如表2所示，利用灰色模型对各层的－10 ℃，－15 ℃下的强度进行预测。

表2 人工冻土单轴抗压强度试验结果

用预测模型对每层土的－10 ℃，－15 ℃下的人工冻土强度进行预测:－10 ℃，－15 ℃下10 个土层的单轴强度由式(1)、式(2)累加生成递增序列，然后把序列代入式(6)～式(9)，求出a，b的值，把求得的a，b值代入(5)式，得到的白化响应式为

－10 ℃下的传统强度白化响应式为

－15 ℃下的传统强度白化响应式为

最后由式(26)或式(27)得到X(1)序列，由式(11)得到预测值。对于改进的预测值，可把传统白化响应式的a，b值代入式(12)、式(13)、式(16)，求得改进的灰色理论预测值，预测结果见表3所示。

对该模型的改进前后进行后差检验，可以得到以下结论:传统的GM(1，1)模型的精度是0.84，检验指标为0.49;改进的GM(1，1)模型的精度是0.87，检验指标为0.43，且达到了精度等级“良好”;由此可知，改进的模型可以应用于人工冻土的单轴强度预测，与传统的模型相比预测精度明显提高。

表3 －10 ℃，－15 ℃下的强度试验值与模型值比较

5 结论

1)改进的灰色模型GM(1，1)应用到人工冻土单轴强度预测，预测精度明显高于传统模型，可以较真实地对人工冻土单轴强度的预测;

2)利用灰色理论进行人工冻土强度预测，须有大量的试验数据，且强度在概率统计的有效范围之内;从而保证数据的有效性;

3)利用灰色理论对人工冻土强度预测是一种趋势预测，存在一定的误差，在实测值序列数值变化幅度较大时，变得较为凸出，可以采用加密数据或建立残差GM(1，1)的方法对数据进行修正。

［1］孙星亮，汪稔，胡明鉴.冻土弹塑性各项异性损伤模型及其损伤分析［J］.岩石力学与工程学报，2005，24(19):3 517－3 523.

［2］李莉，陈鹏宇，段新胜.基坑变形的灰色二次优化模型［J］.辽宁工程大学学报:自然科学版，2010，29(5):926－929.

［3］孙永荣，胡应东，陈武，等.基于GM(1，1)改进模型的建筑物沉降预测［J］.南京航空航天大学学报，2009，41(1):107－110.

［4］贺俊，杨平，董朝文.基于BP 神经网络冻土强度预测模型研究［J］.路基工程，2011，156(3):54－57.

［5］李强，杨平.基于神经网络的声波法预测冻土强度的研究［J］.建井技术，2002，23(6):26－28.

［6］姚兆明，王璇，陈军浩，等.人工冻土单轴抗压强度GA－SVM 预测模型［J］.安徽理工大学学报:自然科学版，2012，32(2):1－5.

［7］马金山，杨兆建基于灰色理论和BP 神经网络的多绳摩擦提升机钢丝绳张力不平衡预测［J］.煤矿机械，2011，32(2):53－55.

［8］褚程程，杨滨滨.灰色理论在矿井用水量预测中的应用［J］.煤田地质与勘探，2012，40(2):55－58.

［9］李宗坤，乔小琴，赵庆.改进的GM(1，1)灰色模型在大坝沉降预测中的应用［J］.浙江水利水电专科学校学报，2010，22(2):1－4.

［10］阎岩，张明义，王家涛.灰色理论在快速法载荷试验数据处理中的应用［J］.岩土力学，2006，27(5):799－802.

［11］蒋刚，林鲁生，刘祖德，等.边坡变形的灰色预测模型［J］.岩土力学，2000，21(3):244－247.

［12］王勇，胡平，申莲，等.GM(1，1)改进模型在大坝位移预测中的应用［J］.云南水力发电，2011，27(2):28－30.