基于简化对称分量法电压选相原理分析＊

蒋晨达

（福建水利电力职业技术学院 电气工程系，福建 永安 366000）

0 引言

选相元件是高压线路保护的重要元件，基于故障分量的选相元件可消除负荷电流的影响，有较突出的优越性［1－2］。目前电力系统广泛采用的故障分量的选相元件有突变量选相和序分量选相，但序分量选相速度慢［3－4］。而利用模故障分量选相不需复数运算，计算速度快。基于暂态保护基本采用模分量进行选相［5］。

本文通过两分量法简化并联故障相模变换和串联故障相模变换，结合克拉克变换、凯伦鲍厄变换等变换阵，提出了一种新的相模变换矩阵。该矩阵的变换阵与反变换阵都是实数，满足频域或者时域变换的条件，时域变换简单，不需复数运算，提高了保护快速反映故障的能力。采用ATP系统仿真模型进行模量意义下的故障定位，验证了新矩阵的正确性以及快速性。

1 并联故障相模变换

电力系统各相间存在电磁耦合关系，为简化计算提出了相模变换实现解耦。电力系统不平衡，可用对称分量变换、克拉克变换、凯伦鲍厄变换等。对称分量变换需进行复数运算，简化对称分量能扩展到具有不平衡负荷或某种不平衡终端的系统上，如并联不对称或串联不对称故障。

1.1 对称分量变换

对称分量变换可将不对称的三相电流或电压分解成正序、负序和零序3个分量。对三相电压的相分量与序分量用式

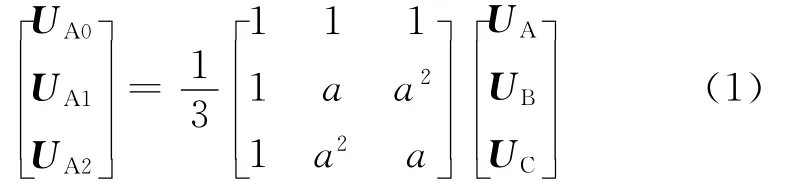
分解［6］。式中，UA1为正序电压分量，UA2为负序电压分量，UA0为零序电压分量。

1.2 两分量法

以三分量法为基础解不平衡系统的两分量法，其前提以正序网络和负序网络的阻抗相等为基础，即假定Z1＝Z2。则电压降方程为

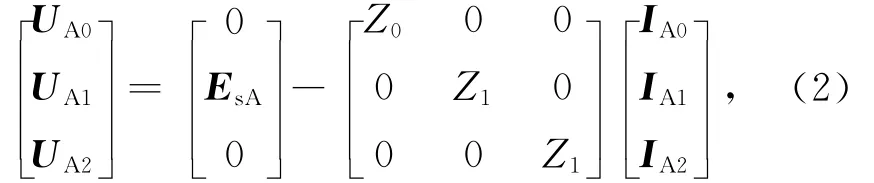
式中，EsA为电源正序电动势，IA1为正序电流分量，IA2为负序电流分量，IA0为零序电流分量。

将式（2）的第2行与第3行相加后代替第2行，第2行与第3行的差代替第3行，得

式中，UA1＋UA2为正序与负序相量和，UA1－UA2为正序与负序相量差。由式（3）建立了以1个零序方程及2个正序方程组成的数学描述，从不对称分量的3个序网络简化为2个序网络，简化了计算过程。

为方便定义电压的和量及差量为

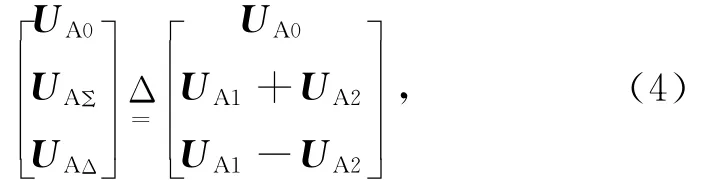
式中，UAΣ为电压的和量，UAΔ为电压的差量。

将式（1）的电压分量的第2和3行进行加、减运算，导出方程为

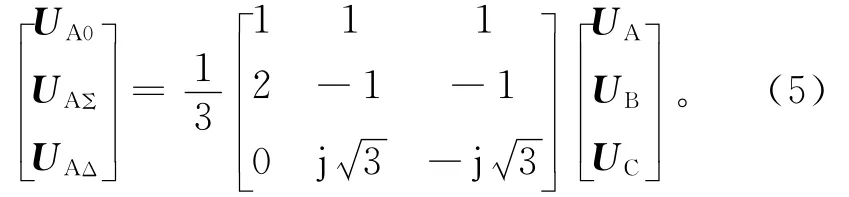
用矩阵表示的变换与反变换阵为

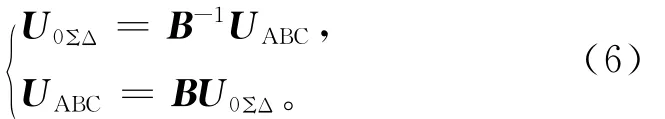
式（6）中B－1，B分别为

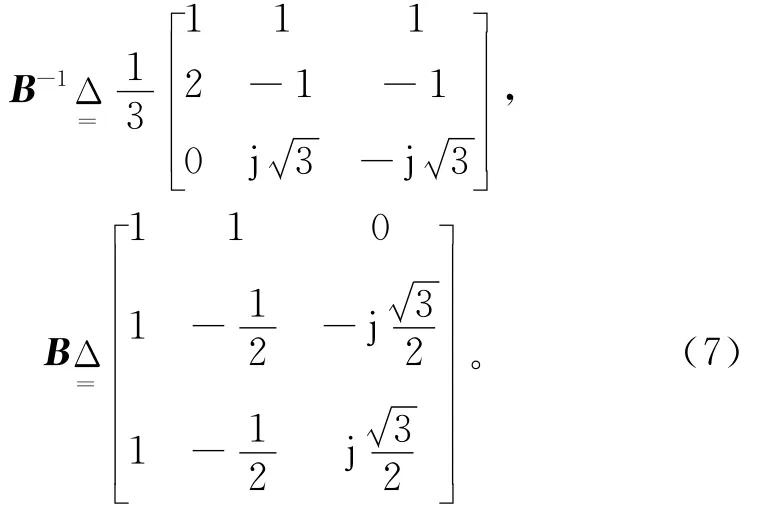
1.3 单相接地故障

设A相金属性接地短路故障，其边界条件为UA＝0。由式（6）得

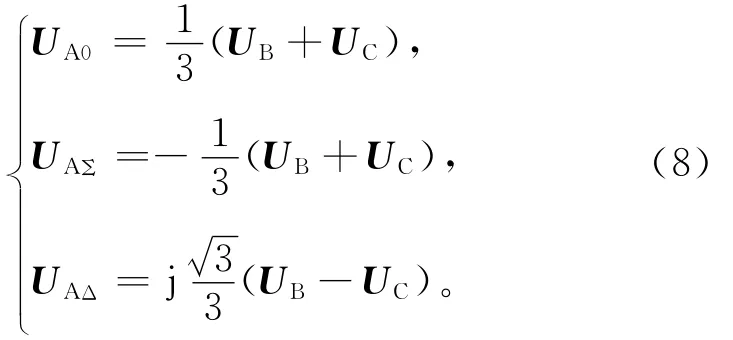
由式（8）得UA0＝－UAΣ。

1.4 两相短路故障

以BC两相短路为例，其边界条件为UB＝UC。将其代入式（5）得

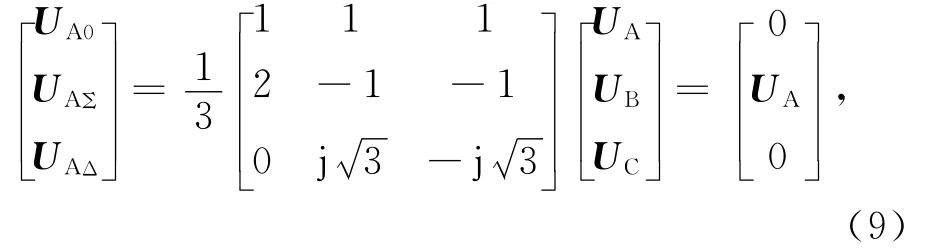
由式（9）知，UA0，UAΔ都为零。

1.5 两相接地短路故障

设BC两相接地短路，其边界条件为UB＝UC＝0，代入式（5）得

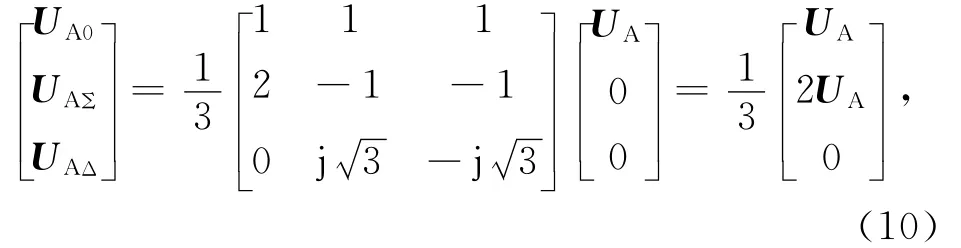
由式（10）得2UA0＝UAΣ，UAΔ＝0。

1.6 三相短路

三相短路边界条件为UA1＝UA，代入式（5）得

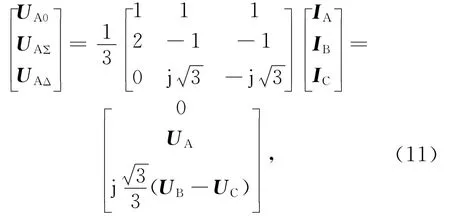
由式（11）知，UA0＝0，UAΣ，UAΔ均不为零。

2 串联故障相模变换

2.1 两相断线

以BC相断线为例，其边界条件为UA＝0，代入式（5）得

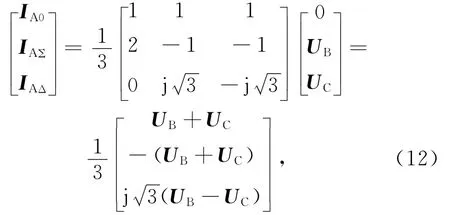
由式（12）得UA0＝－UAΣ。

2.2 单相断线

A相断线的边界条件为UB＝UC＝0，应用式（10）有2UA0＝UAΣ，UAΔ＝0。由并联、串联故障分析表明两相断线与单相接地、单相断线与两相接地故障之间的共同点。可将并联、串联的故障分为2类，一类一相电流为零，另一类两相电流为零。为便于比较将结果列于表1。

表1 零序、和量及差量电压相量关系Table 1 Relationship of zero sequence，amount and differential voltage phasor

3 简化变换

式（7）矩阵满足第1列元素相等，第2列、第3列元素之和为0，该矩阵可以作为平衡矩阵的相模变换阵。克拉克变换、凯伦鲍厄变换等变换阵都满足这种关系［7］。对称分量变换含有复数，适用于频域稳态下的相量分析；克拉克变换、凯伦鲍厄变换阵元素为实数［8］，它们既适用于频域分析，也适用于时域分析。为了使时域和频域变换都适用，本文将变换阵简化为

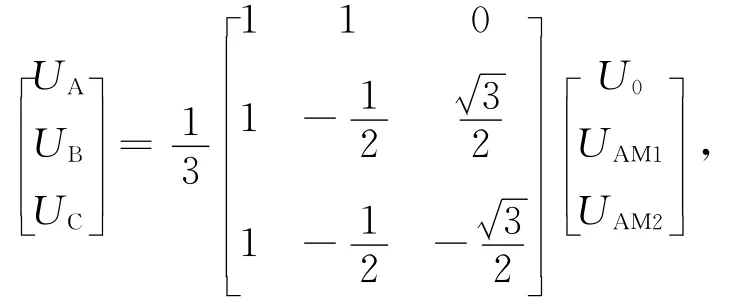
式中，将U0，UAM1，UAM2定义为以A相为特殊相的零模（零序分量）、模1和模2。式（13）变换与反变换阵都是实数，满足频域或时域变换条件。时域变换简单，不需复数运算，提高保护快速反映故障的能力。

3.1 单相接地

A相接地故障时，将边界条件UA＝0代入式（13）得，U0＝－UAM1，UAM2＝ （UB－UC）。

3.2 两相短路

BC两相短路时，边界条件为UB＝UC＝－0.5UA。代入式（13）得，U0＝0，UAM1＝3UA，UAM2＝0。

3.3 两相接地短路故障

BC两相接地短路时，边界条件为UB＝UC＝0，代入式（13）得，2U0＝UAM1，UAM2＝0。

3.4 三相短路

三相短路的边界条件为

UAM1＝3UA，UA＋UB＋UC＝0，代入式（13）得，U0＝0，UAM1，UAM2均不为零。

为分析方便，表2给出了简化后以A相为特殊相接地和相间故障的U0（零序与特殊相选择无关）、UAM1与UAM2的特征量。

表2 A相为特殊相模分量特征Table 2 Phase A is the characteristic of particular phase modal component

同理，以B相和C相为特殊相时，其模变换与以A相为特殊相模变换有相对应结论。表3给出了以B相和C相为特殊相的不对称故障的零模、模1、模2的特征值。

表3 B相和C相为特殊相模分量特征Table 3 Phases B and C are the characteristics of particular phase modal component

4 选相原理

根据上述时域下故障特征，两相接地故障时特殊相模2为0，单相接地故障时特殊相的模1为非故障相电压和的负值；两相短路时特殊相模2为0，对称短路时模1、模2均不为零；接地故障时，零模不为零；根据模1、模2及零模特点可选择故障相别。

当模分量满足U0≠0时，有：

（1）U0＋UAM1＝0，UAM2／UAM1＝－，A相接地故障；U0＋UBM1＝0，UBM2／UBM1＝－，B相接地故障；U＋U＝0，U／U＝－，C相接地故障。0CM1CM2CM1

（2）U＝2U＝2U，U＝0，BC接地故AM10AAM2障；U＝2U＝2U，U＝0，CA 接地故障；BM10BBM2U＝2U＝2U，U＝0，AB接地故障。CM10CCM2

当模分量满足U0＝0时，有：

（1）U＝0，U≠0，BC相间故障；U＝AM2AM1BM20，U≠0，CA相间故障；U＝0，U≠0，ABBM1CM2CM1相间故障。

（2）UAM1＝3UA，UAM2＝（UB－UC），则判三相短路故障。

根据上述理论分析，用简化对称分量法电压选相原理流程如图1所示。

本文利用ATP软件对双侧电源系统110kV线路进行了验证，图2为仿真模型。图2中F为短路点，线路长度为86km，单位长度正序电抗X1＝0.4 Ω／km，单位长度零序电抗X0＝0.92Ω／km，单位长度正序电阻r1＝0.027Ω／km，单位长度零序电阻r0＝0.694Ω／km；M 侧电源等效电阻RM1＝16Ω，电源EM＝110kV∠45°，电源正、负阻抗相对值为0.076，零序阻抗相对值为0.113；电源EN＝105kV∠15°，正、负阻抗相对值为0.15，零序阻抗相对值为0.1；基准容量为100MVA，基准电流为502A。分别对距离保护安装处 M侧30，50，70km发生单相、两相、两相接地、三相短路故障进行仿真。仿真验证时采样的频率选用600Hz，连续判别3次，在6 ms内作出判断，结果与理论分析完全相符。

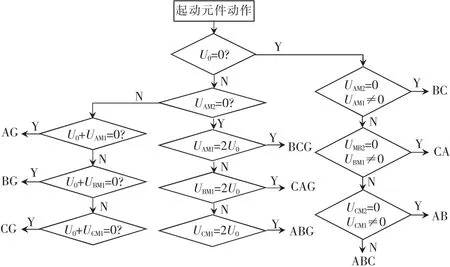
图1 选相流程框图Fig.1 A picture of phase selecting process

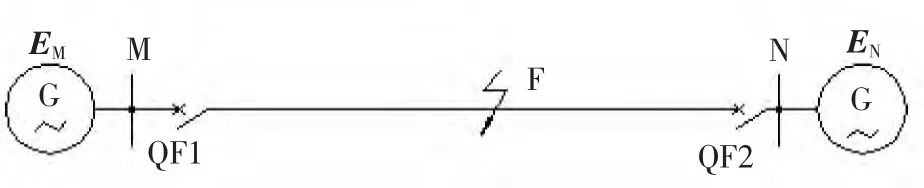
图2 仿真模型Fig.2 Simulation mkdel

5 结语

本文讨论了简化对称分量电压模分量之间的关系，将三序分量简化为零序和正序两分量，序网络数目从3个减少为2个，可以解任何并联或串联不平衡故障；分析各种类型短路模电压分量的特性，提出了利用电压模分量的选相原理。该选相元件动作快速，可用于高压、超高压线路暂态保护，并通过仿真验证了该方案的可行性和有效性。

［1］ 许正亚.输电线路新型距离保护［M］.北京：中国水利水电出版社，2002.

［2］ 黄瑞梅，张国良，许建安.输电线路故障选相方案探讨［J］.水电能源科学，2009，27（3）：193－195.

［3］ 索南加乐，许庆强，李小斌，等.电力系统振荡过程中序分量选相元件动作行为分析［J］.电力系统自动化，2003，27（7）：50－54.

［4］ 王兴国，黄少锋，流千宽.一种利用电压模故障分量的选相元件［J］.电力系统自动化，2008，32（9）：42－46.

［5］ 葛耀中.新型继电保护和故障测距的原理与技术［M］.西安：西安交通大学出版社，2007.

［6］ 许建安，王风华.电力系统继电保护整定计算［M］.北京：中国水利水电出版社，2007.

［7］ 和敬涵，张飑，范瑜，等.解耦变换在电力系统暂态保护中的应用研究［J］.北京交通大学学报，2006，30（5）：101－104.

［8］ 徐振宇，杨奇逊，万顺，等.一种新型数字式故障选相元件［J］.中国电机工程学报，1997，17（3）：214－216.

［9］ 杨武盖.基于对称分量突变量距离保护［J］.淮海工学院学报：自然科学版，2014，23（1）：25－29.