基于CHNN的地图四着色算法*
高 勇,李存华
(淮海工学院 计算机工程学院,江苏 连云港 222005)
0 引言
一个图,如果可以将它画在平面上,使它的边仅在端点上才能相交,则称此图为可平面图。如果一个可平面图的每一个面都是三角形,则它是最大可平面图。地图的四着色问题最终可归结到最大可平面图的顶点四着色问题,这一点,图论的众多文献中都有介绍[1],本文不再论述。最大可平面图的顶点四着色,当顶点数较多时,计算量太大,人工着色的办法根本不可能,而利用神经网络方法进行编程是可行的。
1 神经网络方法
人工神经网络方法是一种模仿动物脑神经网络某些功能的数值计算方法。人工神经网络的结构由神经元和神经元间的连接权组成,多数类型的神经网络将神经元以层的形式组织在一起,常见的神经元间的连接权以层间神经元的连接权为主。目前应用最广泛的反向传播神经网络,其结构由输入层、输出层和至少一个隐含层,以及层间连接权组成[2]。反馈网络有多种,霍普菲尔德网络是单层对称全反馈网络,根据其激活函数的选取不同,可分为离散型的霍普菲尔德网络(DHNN)和连续型的霍普菲尔德网络(CHNN)。DHNN的激活函数为二值型的,其输入、输出为{-1,1}的反馈网络,主要用于联想记忆;CHNN的激活函数为连续可微的单调上升函数,主要用于优化计算(如图1所示)。
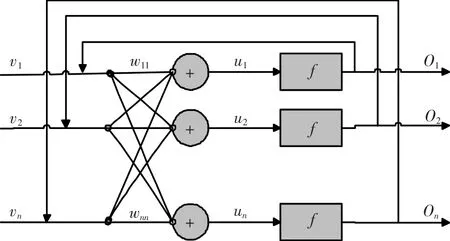
图1 霍普菲尔德网络结构示意图Fig.1 Schematic diagram of Hopfield neural network
霍普菲尔德网络是和电子模拟线路对应的,其中每一个神经元都有一样的电路模型。它的工作原理有一定的动态数学方程,其能量函数可正可负,但负向有界,是广义的李雅普诺夫函数,如图1和图2所示。
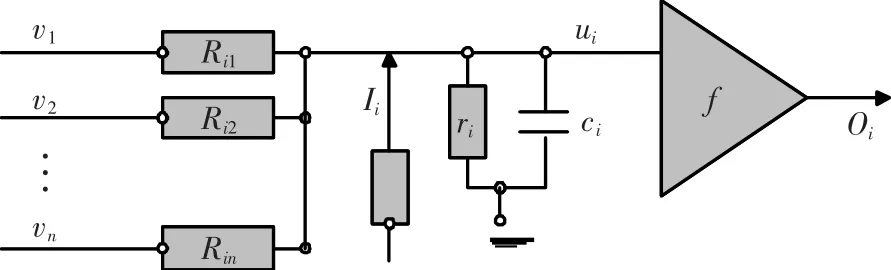
图2 神经元电路模型示意图(第i个)Fig.2 Schematic diagram of neuron circuit model(i)
Rij为第j个输入与第i个输入之间的连接导纳,Wij=1/Rij;ri与ci分别为第i个运算放大器的电阻和输入电容;Ii为外加恒定电流。调节其他系数,可忽略余项。V是输入矢量,U是状态矢量,O是输出矢量。
输出:
f(ui)= (1+tanh(λ×ui))/2;
动态方程:
dui/dt= (-ui/qi+ ∑Wijvj+Ii)/ci,1/qi=1/ri+ ∑Wij;
能量函数:
E=-(∑Wijvivj)/2-∑viIi+余项。
2 四着色问题的CHNN的网络设计
2.1 反馈网络的稳定状态
反馈网络能够表现出非线性动力学系统的动态特性,它具有如下的主要特性。
(1)网络系统具有若干个稳定的平衡状态。当网络从某一个初始状态开始运动后,网络系统总可以收敛到某一个稳定的平衡状态。
(2)系统稳定的平衡状态可以通过设计网络的权值而被存储到网络中[3]。
假设一个最大可平面图已被四着色成功,那么它的每一个顶点颜色与其相邻的顶点颜色都不相同,这是一种稳定状态,其他情况可视为不稳定状态。因此,顶点颜色状态矩阵需要满足3个条件:
(1)每列只能有一个是1。
(2)1的总数必须与顶点数相符。
(3)若某点的一个颜色模式为1,则与其连接的所有顶点的这个模式都不能为1。示例见表1。
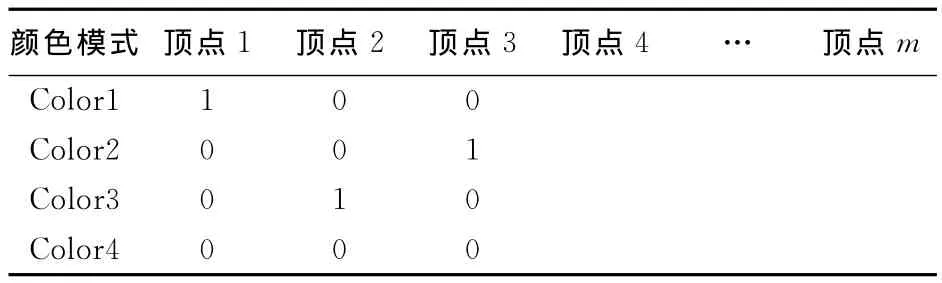
表1 顶点颜色状态表Table 1 Model table of vertex color
2.2 神经元设计
对于m个顶点,需要4m个神经元,设n=4m,则描述CHNN的动态方程如下。

其中,T为CHNN网络连接矩阵,λ为增益参数,τ是各神经元的时间常数。
2.3 网络设计
设G为最大平面图的连接矩阵;g(a,b)=0表示第a个顶点与第b个顶点不连接;g(a,b)=1表示第a个顶点与第b个顶点连接。则T设计为
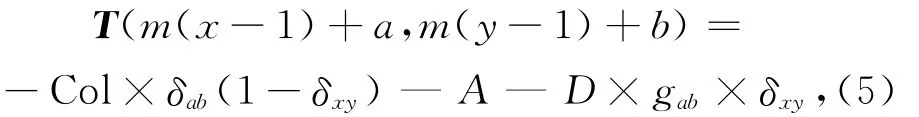
其中,Col为列限制系数常量,A为全局限制系数常量,D为平面图结构限制系数常量。a,b取1到m的值;a=b意味同一顶点,δab=1;a≠b,δab=0。x,y取1到4的值;x=y意味同一颜色,δxy=1;x≠y,δxy=0。
3 实验验证
3.1 实验程序
程序主要由以下5个部分组成。
(1)随机生成最大可平面图。
(2)网络中有关矩阵的生成。
(3)迭代计算。
(4)根据计算结果对顶点进行染色。
(5)参数设定模块。参数设定模块主要迭代计算的伪代码如下。
初始化:① 按公式(5)设置连接矩阵;② 以零设置输入和状态值。
cok:=false;//cok表示着色是否成功
dt:=0.01;
while(idx<nMax)do begin
//nMax为迭代次数限制
//状态的计算;tt,II,dt分别对应参数τ,I,Δt
for k:=1to 4*DDN do begin
//DDN为实际顶点数
tmp:=0;
for j:=1to 4*DDN do
tmp:=tmp+T[k,j]*V[j];
U[k]:=U[k]+
(tmp-U[k]/tt+II)*dt;//参照公式(4)end;
//利用激活函数计算反馈;lmd为参数λ
for k:=1to 4*DDN do begin
V[k]:=(1+tanh(lmd*U[k]))/2;
//参照公式(2)
end;
//顶点颜色的计算;CoT为顶点颜色状态表
for i:=1to DDN do
for j:=1to 4do
CoT[j,i]:=V[(j-1)*DDN+i];
for k:=1to DDN do begin
max:=-1;maxi:=0;
for i:=1to 4do
if CoT[i,k]>max then begin
max:=F[i,k];maxi:=i;
end;
Se[k]:=maxi;//顶点所着颜色(次号)
end;
//判断是否着色成功
i:=1;
while i<=DDN do begin
j:=1;
while j<=DDN do begin
if(G[i][j]=1)and(Se[i]=Se[j])then
break;
j:=j+1;
end;
if j<=DDN then break;
i:=i+1;
end;
if i>DDN then break;
idx:=idx+1;
end;
cok:=(idx<nMax);//cok为 True表示着色成功。
3.2 实验参数和着色示例
在实验中,随机产生了100个顶点的最大可平面图,使用表2的最后一行数据为运行参数,经过大约20 599次迭代以后,成功染色,运行时间大约为180s。图3中的空圆圈、实心圆圈、空方块、实心方块分别代表4种不同的颜色。在参数表中,参数Col,A和D用于网络矩阵T的初始化计算;参数λ,τ,和I用于迭代计算[4]。U和V的初始值可以为零。本程序使用Delphi2010实现,如图3所示为实验着色的结果。
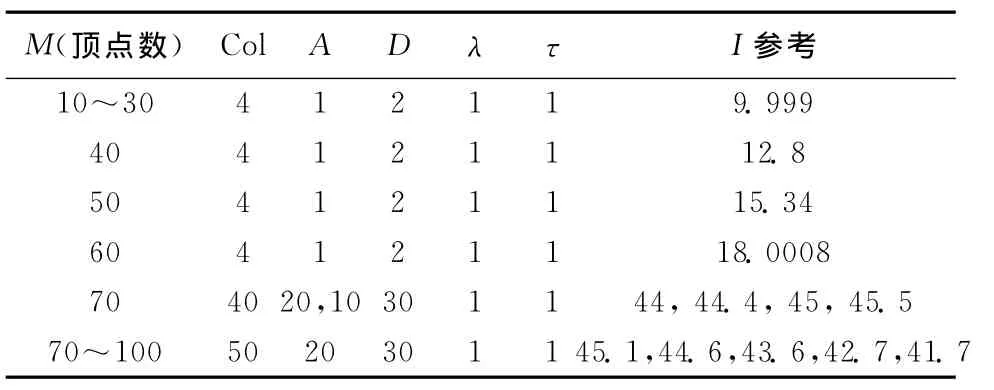
表2 运行参数表Table 2 Running parameter table
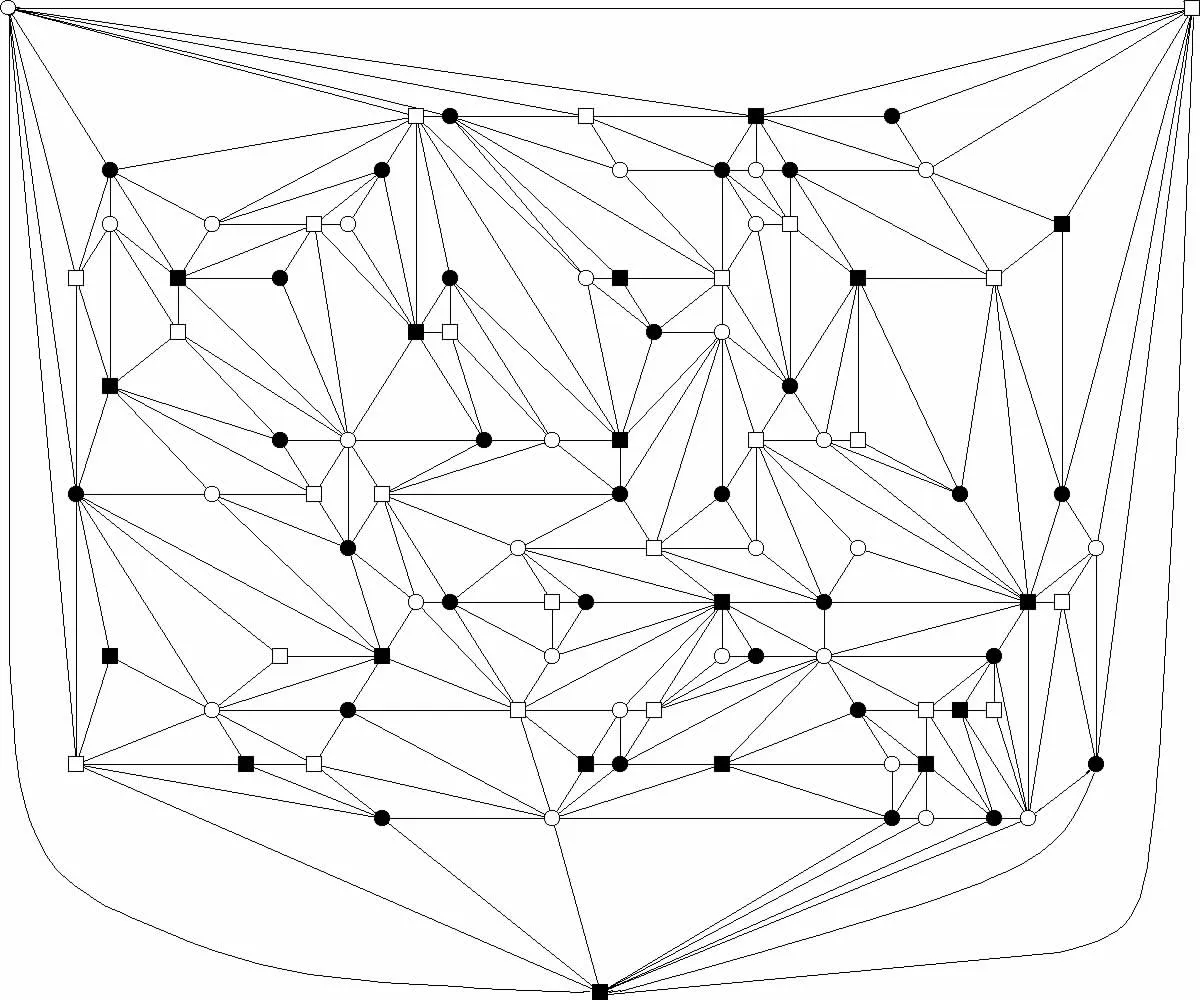
图3 100个顶点的着色结果Fig.3 Coloring result of one hundred vertexes
4 结论
霍普菲尔德神经网络已成功地应用于多种场合,主要集中于图像处理、语音处理、信号处理、数据查询、容错计算、模式分类、模式识别等[5]。霍普菲尔德认为,在系统的运动过程中,其内部储存的能量随着时间的增加而逐渐减少,当运动到平衡状态时系统的能量耗尽或变得最少,那么系统自然在此平衡状态稳定下来。利用能量函数概念,可以设计CHNN进行优化计算,利用其并行性可解决计算中的“指数爆炸”问题。典型例子是TSP问题、旅行商问题。本文探讨更复杂的四着色问题,希望能给图论研究带来一点启示。
[1] 杨炳儒.图论概要[M].天津:天津科学技术大学出版社,1990.
[2] HAYKIN S.神经网络原理[M].北京:机械工业出版社,2004.
[3] 魏海坤.神经网络结构设计的理论与方法[M].北京:国防工业出版社,2005.
[4] TALAVAN P M,JAVIER.Parameter setting of the Hopfield network applied to TSP[J].Neural Networks,2002,15(1):363-373.
[5] KURITA N,FUNAHASHI K-I.On the Hopfield neural networks and mean field theory[J].Neural Networks,1996,9(9):1531-1540.

