拟阵交构约束的下模函数最大值问题的近似算法及其分析＊

张立群

（兰州交通大学 数理与软件工程学院，甘肃 兰州 730070）

0 引言

组合优化问题是在给定的有限集所具备的某些条件的子集中，按某种目标找出一个最优符合标准的一类数学规划问题［1］.所研究的问题涉及电路设计问题、运输线路问题、装箱问题［2］等很多领域.下模函数是一类定义在有限的幂集上或格上的相对比较特殊的实值函数，下模函数的最值研究在组合优化中起着重要的作用.

下模函数定义如下：给定一个有限集E和定义在E上的幂集合2E上的一个函数f：2E→Z，这里2E是由E的所有2｜E｜个子集组成的集合，如果对于E中任意两个集合A和B，都满足不等式

f（A）＋f（B）≥f（A∩B）＋f（A∪B），则称f（·）是一个下模函数.

本文考虑求解m个拟阵交构成的独立系统约束下的下模函数的最大值问题，即

OPT＝ max｛f（S），S∈F｝，

其中（E，F）是由m个拟阵的交构成的独立系统.

1 若干定义、引理及其证明

定义1 设E是一个有限集合，L是E的一个子集族，若满足I∈L且I′⊆I，则I′∈L，称L中子集为独立子集，称（E，L）是一个独立系统.

定义2 设E是一个有限集合，L是一族E的子集合.如果（E，L）满足两个条件：

（1）若I∈L且I′⊆I，则I′∈L；

（2）对于E中的任意一个子集F，有u（F）＝v（F）；

就称其是一个拟阵.

给定E的一个子集F，若F的任意一个独立子集都不严格包含子集I⊆F，则称I是F的一个极大独立子集.对任意集合I⊆E，令｜I｜表示I中所包含元素的个数.定义：

u（F）≡min｛｜I｜，I是F的一个极大独立子集｝，v（F）≡max｛｜I｜，I是F的一个独立子集｝.

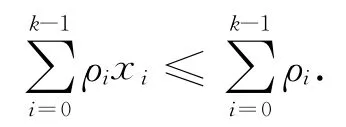
证明 考虑以下给出的线性规划：

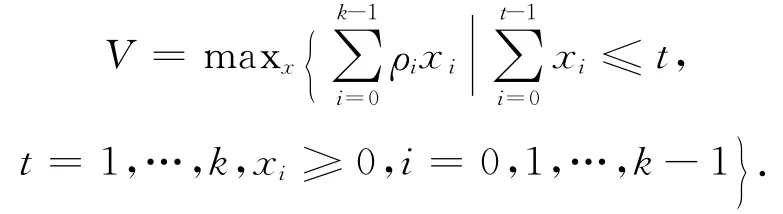
容易得到其对偶规划为

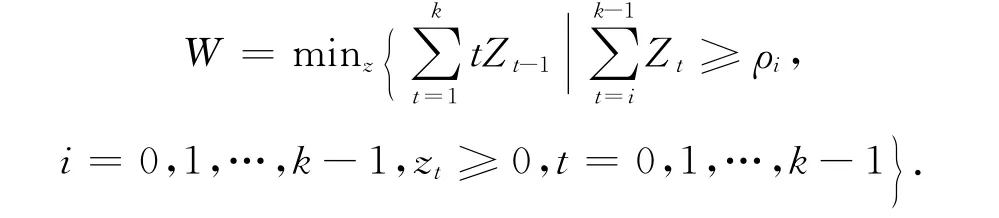
由于ρi≥ρi＋1，Zi＝ρi－ρi＋1，i＝1，2，…，k－1，ρk＝0是对偶可行解，其最优值为，由线性规划的对偶定理，易说明引理成立.

2 给出近似算法及其性能保证

OPT＝max｛f（S），S∈F｝，其中（E，F）是由m个拟阵的交构成的独立系统.

给出近似算法及其近似度分析，求解fS｜F的近似算法示意［5］如下：

第1步 令i＝1，S0＝Ø，E0＝E；

第2步 若Ei－1＝Ø，则停止计算；

第3步 求ei∈Ei－1，使其满足α·ρeij（Si－1）≥maxe∈Ei－1ρe（Si－1），α＞0；

第4步 判断Si－1∪ ｛ei｝是否属于F；

第5步 若Si－1∪ ｛ei｝不属于F，则令Ei－1＝Ei－1＼｛ei｝，返回第2步；

若Si－1∪ ｛ei｝∈F，则令Si＝Si－1∪ ｛ei｝，ρi－1＝ρei（Si－1），Ei＝Ei－1＼｛ei｝；

第6步 令i＝i＋1，返回第2步.

下面继续给出用近似算法求出的近似解的近似度分析.

定理 设（E，F）是一个由m个拟阵的交集相对独立地构成的系统，f是定义在Ω上的非负非减下模函数［4］.如果将Zg与OPT分别记作是通过以上近似算法得到的目标函数值和目标函数最优解，那么有

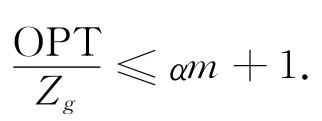
证明 设S和T分别是问题fS｜F近似算法的解和最优解，｜S｜＜k，由于（E，F）是一个独立的系统，并不一定是拟阵，因此｜T｜不一定是k.

对于t＝1，2，…，k，令St－1＝T∩ （Ut＼Ut－1） ，Ut是第t次迭代得到的解集.为不失一般性，设U0＝ Ø，Uk＝E，ρ＊（Si）＝ maxe∈Eiρe（Si），i＝1，2，…，k－1.

由于f是非负非减的下模函数，由引理2可以得到如下关系：

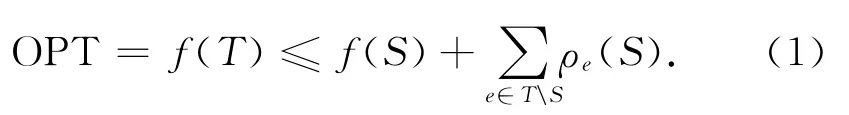
设t∈ ｛1，2，3，…，k｝，ρq（t）＝min｛ρi｜i＝1，2，…，t－1｝.对任意e∈T∩ （Ut＼Ut－1），由于f具有下模性，所以有

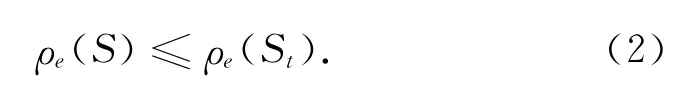
由ρ＊的定义和算法可得：ρe（S）≤ρe（St）≤ρ＊（St）≤ρ＊（Sq）（t）＋1）≤αρq（t）.

令ρ′t－1＝αρq（t），则有

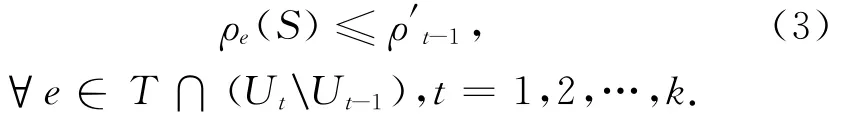
由于q（t）具有非增性，所以ρ′t－1也具有非增性，即ρ′t－1≥ρ′t.另一方面

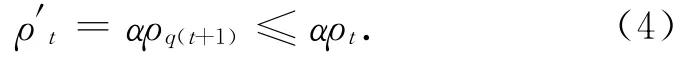
由上述不等式（1）和（2）可得

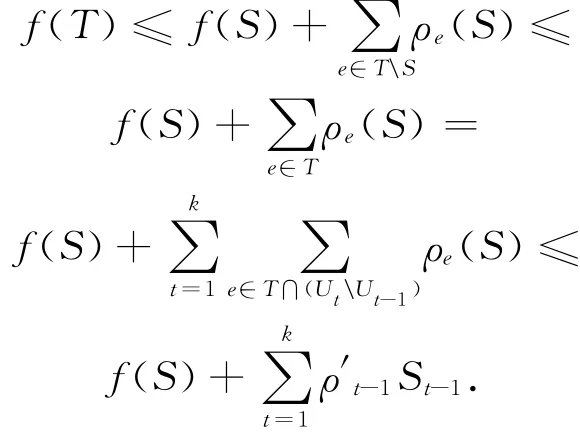
注意到St－1∈T∩ （Ut＼Ut－1） ，则有＝T∩Ut.

由于T是拟阵的独立集，rM（SPM（St））＝t，，于是有

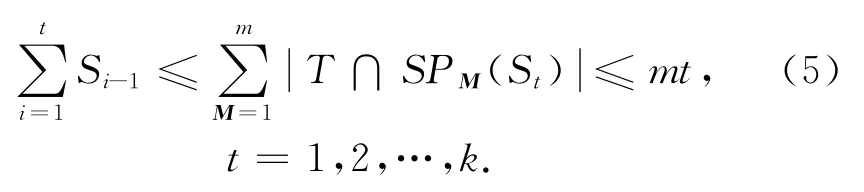
因为对 ∀t，ρ′t，St≥0，ρ′t具有非增性，在引理2中，令，由上述不等式（5）有

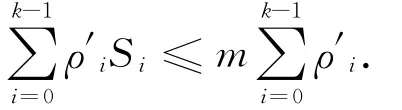
再由不等式（4）得

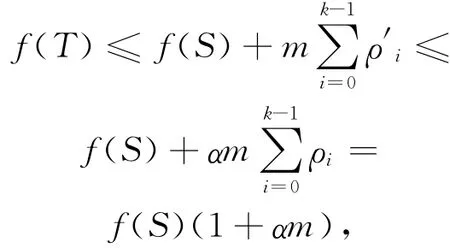
即

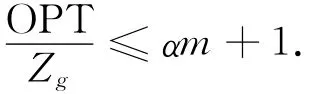
［1］ 陈宝林.最优化理论与算法［M］.北京：清华大学出版社，2006.

［2］ 罗亮，贾欣鑫，何尚录，等.求解组合拍卖问题最大值的贪婪算法［J］.黑龙江科技学院学报，2008，18（5）：382－384.

［3］ FISHER M L，NEMHAUSER G L，WOLSEY L A，et al.An analysis of approximations for maximizing submodular set functions－II［J］.Mathematical Programming Study，1978，8：73－87.

［4］ SVIRIDENKO M.A note on maximizing a submodular set function subject to knapsack constraint［J］.Operations Research Letters，2004，32：41－43.

［5］ 王武民，张防防，柘晓莉，等.求解下模集函数最大值问题的局部搜索算法［J］.温州大学学报：自然科学版，2008，29（3）：12－17.