AES加密算法的Sbox设计分析及其改进*-
汪培芬
(淮安市广播电视大学 信息工程系,江苏 淮安 223002)
AES(advanced encryption standard,AES)加密算法即密码学中的高级加密标准,代表着最新的编码技术[1],又称Rijndael加密算法,已在现今社会各个领域中得到广泛应用。它是一种对称密钥的加密算法,其密钥长度可达256bit,且用128bit分组加密和解密数据。S-box(substitution box)作为实现数据非线性置换的组件在AES密码设计中有着重要地位,S-box为分组密码算法提供混合层,同时对抵抗各种攻击起关键性的作用。在对长度为128 bit的明文加密运算中,S-box共用到160次,所以它的安全性直接影响到整个密码的安全性[2]。
1 S-box设计分析
为保证整个密码系统的安全性,以抵抗各种可能的攻击,S-box在设计时考虑到差分密码分析和线性密码分析的要求。虽然S-box的设计原理是保密的,但它满足4个方面的条件:①可逆变换;②输入比特和输出比特的线性组合之间的最大非平凡相关性极小化;③ 异或差分表中的最大非平凡值的极小化;④ 在GF(28)上的代数表示的复杂性。
AES中S-box主要运算是独立地对状态中的每个字节进行非线性字节变换。具体有2个步骤:① 求GF(28)有限域内各元素的乘法逆元。aij代表状态中的第i行第j列的一个字节,ai-j1则是aij在GF(28)上的乘法逆。将状态中的每个字节aij看作GF(28)上的元素,映射到自己的乘法逆ai-j1,0字节映射到它自身。② 做仿射变换。将字节做(GF(2)上可逆的)仿射变换,

即
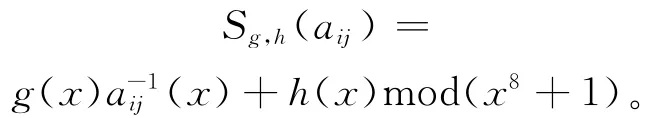
为了便于叙述,给出GF(28)中表示方法
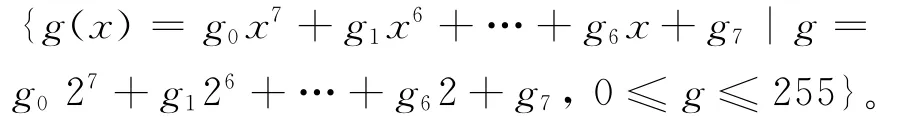
在AES中取
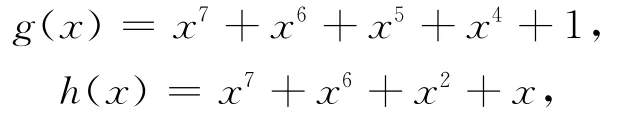
仿射变换对为(143,99)。常量(01100011)2的选择确保了S-box没有不动点S-box(a)=a和对立不动点S-box(a)=。输入比特的线性组合与输出比特的线性组合之间的最大非平凡相关性是2-3,异或差分表的非平凡最大输出差分概率是2-6,S-box具有抵抗线性攻击和差分攻击的能力。
S-box变换S143,99:GF(28)→GF(28)后每个元的对应值见表1。
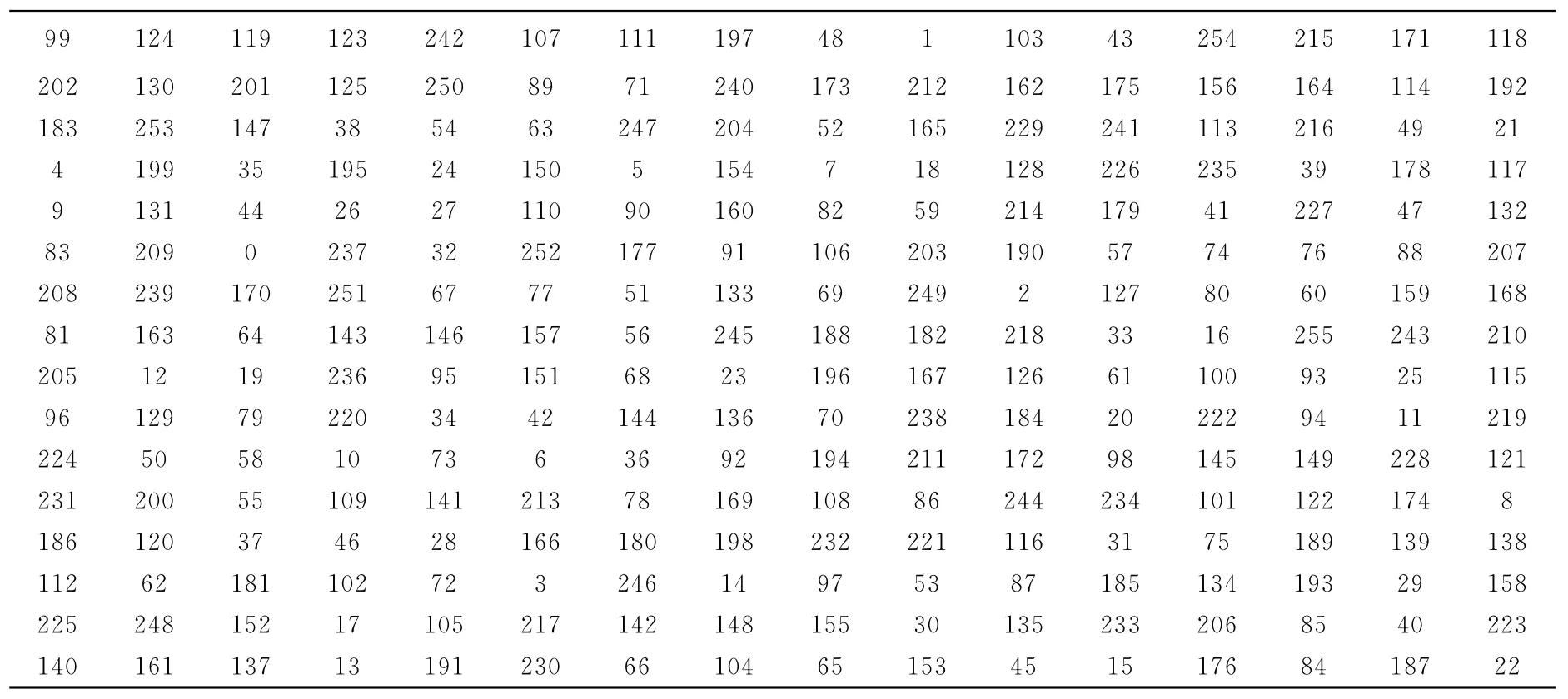
表1 S-box对应值表Table 1 Corresponding S-box value table
2 S-box的循环迭代周期分析
对GF(28)的每个元做 S-box循环迭代,即,m=0,1,…,255,n为循环迭代次数。例如,若m为3,那么:n= 1,2,…,59}= {123,33,253,84,32,183,169,211,102,51,195,46,49,199,198,180,141,93,76,41,165,6,111,168,194,37,63,117,157,94,88,106,2,119,245,230,142,25,212,72,82,0,99,251,15,118,56,7,197,166,36,54,5,107,127,210,181,213,3},由此可见,经过 59 次S143,99:GF(28)→GF(28)的循环迭代,对应元重新回到3,形成了一个周期为59的循环迭代。
同理,当m为不同的元时,得到下列循环迭代:,经过2次迭代,对应元回到143,周期为2。n=1,2,…,27}= {239,223,158,11,43,241,161,50,35,38,247,104,69,110,159,219,185,86,177,200,232,155,20,250,45,216,97},经过27次迭代,对应元回到97,周期为27。= {124,16,202,116,146,79,132,95,207,138,126,243,13,215,14,171,98,170,172,145,129,12,254,187,234,135,23,240,140,100,67,26,162,58,128,205,189,122,218,87,91,57,18,201,221,193,120,188,101,77,227,17,130,19,125,255,22,71,160,224,225,248,65,131,236,206,139,61,39,204,75,179,109,60,235,233,30,114,64,9,1},经过81次迭代,对应元回到1,周期为81。= {103,133,151,136,196,28,156,222,29,164,73,59,226,152,70,90,190,174,228,105,249,153,238,40,52,24,173,149,42,229,217,53,150,144,96,208,112,81,209,62,178,55,154,184,108,80,83,237,85,252,176,231,148,34,147,220,134,68,27,175,121,182,78,47,21,89,203,31,192,186,244,191,8,48,4,242,137,167,92,74,214,246,66,44,113,163,9},经 过87次迭代,对应元回到9,周期为87。
由以上分析可得,每个元只属于2,27,59,81,87中的一个周期,最短周期为2,最长周期为87,对于GF(28)的256个空间来说,周期太短。这就像DES(data encryption standard,DES)算法的S-box迭代输出不能遍历所有的可能值,而导致有力的差分攻击一样。虽然AES加密算法的其他层可以掩盖S-box迭代短周期的特点,但是随着技术的进步和密码破译算法的发展,这种周期性的缺点可能被密码分析所利用,AES的短周期一样存在着差分攻击的可能。所以,S-box的短周期性应该被完善[4]。
3 S-box的改进方案
针对S-box存在迭代短周期的问题,本文提出了改进的方案。
为了得到所有可能值的S-box的迭代输出,就要求每个元在GF(28)空间中的迭代循环周期数都达到GF(28)空间的容量256,即在GF(28)空间中所有元只属于一个迭代循环。本文改进设计,得到如下改进后的仿射变换。
m(x)=x8+1不变,
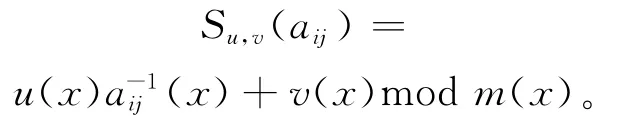
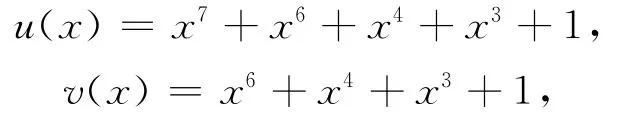
改进取即取u=155,v=154,用仿射变换对(155,154)替换原来S-box的仿射变换对(143,99),先求乘法逆元后进行仿射变换。
(1)将字节看作GF(28)上的元素,映射到自己的乘法逆,0字节映射到它自身。
(2)将字节做GF(2)上的仿射变换。

经过256次S′n155,154:GF(28)→GF(28)的循环迭代,对应元重新回到9,形成了一个周期为256的循环迭代,遍历了空间中的每一个值,经过测试,其他元循环迭代周期也为256。
改进的S-box变换后对应值如表2所示。
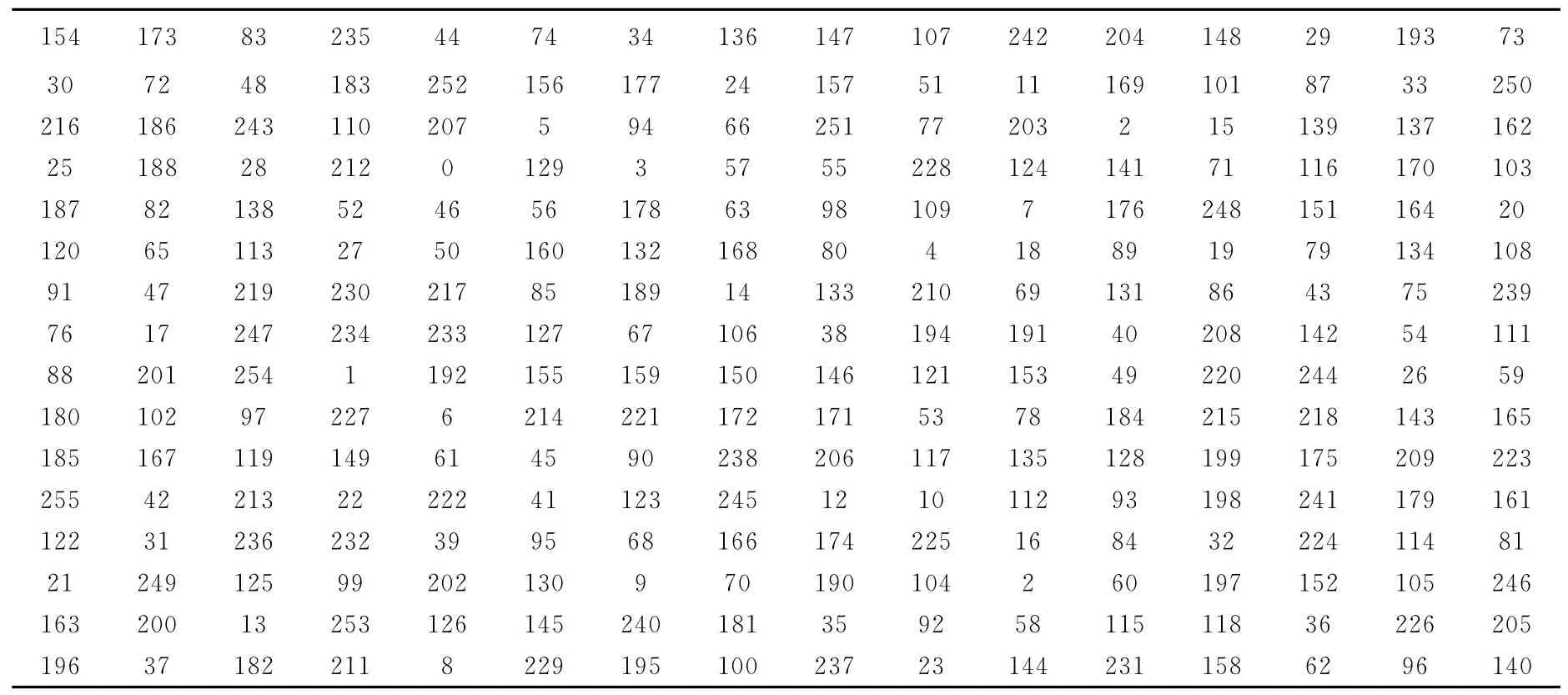
表2 改进的S-box替换表Table 2 Improved S-box substitution table
4 结束语
S-box作为AES加密算法中唯一的非线性元件,其安全性能的好坏直接决定着整个分组密码性能的好坏,一个良好的S-box能提高加密算法抵抗各种密码分析攻击的能力。本文对AES的S-box设计进行了分析,指出其循环迭代输出周期过短的特性,并且提出一种切实可行的方案,使得迭代周期扩大到256整个空间,从而提高了算法的安全性。
[1] 赵雪梅.AES加密算法的实现及应用[J].常熟理工学院学报,2010,24(2):105-110.
[2] 吴文玲,冯登国,张文.分组密码的设计与分析[M].北京:清华大学出版社,2009.
[3] 王衍波.AES的结构及其S-box分析[J].解放军理工大学学报:自然科学版,2002,3(3):13-17.
[4] BASSHAM L.NIST efficiency testing of ANSI Cimp lamentations of round 2AES candidate algorithms for the advanced encryption standard[C]//The Third AES Candidate Conference.Gaithersburg,MD:the National Institute of Standards and Technology,2000:136-148.
[5] 孙爱娟.基于AES加密算法的改进及其 MATLAB实现[D].哈尔滨:哈尔滨理工大学,2009.

