基于马尔科夫模型的线路OD矩阵的研究＊

吕卫东

（兰州交通大学 数理学院，甘肃 兰州 730070）

0 引言

所谓公交线路OD矩阵，是指乘客从出发地（Origin）到目的地（Destination）的出行矩阵.OD矩阵提供了流动的车辆或人流从一个特定区域到另一个区域的基本信息，它在交通及交通运输管理上发挥着至关重要的作用，是进行交通流量分配的前提.而获取OD出行分布矩阵是一项十分复杂而艰巨的工作.如何经济有效地获取可以用于交通管理和控制的OD矩阵是近年来国内外研究的一个热点课题.传统的OD矩阵的获取是通过大规模的抽样调查，由于交通量数据十分庞大，这项工作即使是作抽样调查，也将耗费大量的人力、物力、财力以及时间，而且所取得的数据精度难以保证，数据更新时间也长.目前利用已观测到的路段交通量和一些先验信息（如历史的OD矩阵）来估计未知的OD矩阵是一种效率高、周期短的OD矩阵获取技术.这方面的研究成果［1－6］主要有：以最大熵为原理的最大熵（ME）模型；以最小二乘为原理的最小二乘（GLS）模型；以最小信息量为基础的最小信息量（IM）模型；以极大似然原理为基础的极大似然（ML）模型；基于随机模拟的遗传算法模型等.

采用马尔科夫模型来估计线路OD矩阵［7］的优点是，在计算时需要估计的参数较少。这样就使得该计算方法较为高效，计算方法简单，易于在计算机上实现.并可证明，用这种方法估计出的数据与极大熵模型得出的结论是相近的.

1 基于马尔科夫模型的线路OD矩阵的计算

考虑一条设有N个站点的公交线路运送乘客上下车，在假设调查已知旅客在各站上下车的人数情况下，计算出在第i站上车第j站下车（j＞i）的乘客数量.

1.1 乘客的数量

设yi是在第i站上车的乘客的数量（i＝1，…，N），设zj是在第j站下车的乘客的数量（j＝1，…，N）.并设在第N站没有乘客上车，即yN＝0；在第1站没有乘客下车，即z1＝0.定义xij是需要计算的在第i站上车在第j站下车（i，j＝1，2，…，N）的乘客数量.

图1给出了这种公交线路的图示.

图1 公交线路Fig.1 Bus lines

由此，容易得出如下结论［4］

1.2 马尔科夫模型

以下通过马尔科夫模型来估计未知的上下车概率矩阵P＝ （pij）N×N.为了利用马尔科夫模型的无后性计算出矩阵P，因此在这里一名乘客在第i－1站上车在第i站下车的概率就是至关重要的.一旦上下车的概率矩阵P被估计出来，就可以计算出所需的OD矩阵X＝ （xij）N×N.这种方法的优点就在于，计算上下车概率矩阵P只需要知道在各站上车和下车的乘客数，而这样的数据是容易获得的.

马尔科夫模型是指某一变量将来的状态只与现在的状态有关，而与过去的状态无关.其中将来、过去和现在的状态彼此相互独立.在马尔科夫模型中，转移概率的计算是最为重要的.假设ξi是一个随机变量，代表一名乘客在第i站的状态.在第i站当乘客在车上时，记作ξi＝1，否则记作ξi＝0.

马尔科夫模型中的马尔科夫转移概率作如下的定义：

其中qi为一名乘客在第i－1站上车在第i站下车的概率.显然qN＝0，由马尔可夫转移概率的计算原理，乘客上下车的概率矩阵P＝（pij），可由如下方法计算得出.

首先，在第1站，根据定义有p12＝q2，根据马尔科夫模型的性质，有

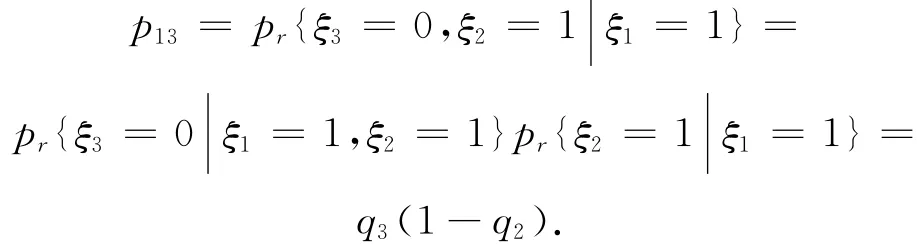
以此类推，在第i站（i＝1，…，N－1），有

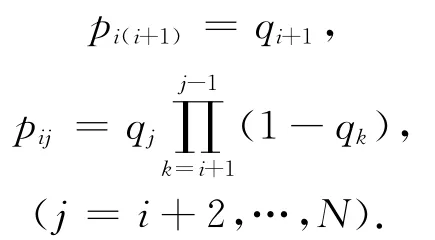
一旦上下车的概率矩阵被计算出来，就可以按照如下公式计算出公交线路上从第i站上车到第j站下车的乘客数：

当i≥j时ij＝0.

为了计算pij，首先需要计算出qj的值.以下采用极大似然估计的方法估计qj的值.车辆在第j站时乘客的总数为

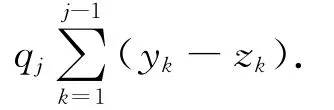
所以在第j站下车的乘客数zj应遵循二项分布，由极大似然估计得出的qj的值

由下式给出：

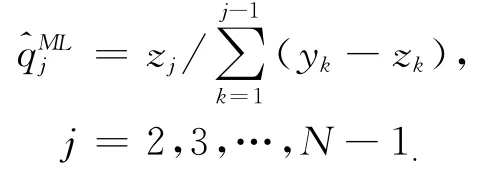
2 结束语

线路OD矩阵的调查需要耗费大量的人力、物力、财力，利用可以获得的数据致力于OD矩阵的研究是国内外许多学者的研究领域.本文利用调查上下车乘客的人数，根据马尔可夫模型给出了一种推算OD矩阵的方法.采用本文推算方法对当地公交线路进行调查，得到了完整可行的OD矩阵.说明本文的推算方法是可行的.

［1］ 窦慧丽，刘好德，杨晓光.基于站点上下客人数的公交客流OD反推方法研究［J］.交通与计算机，2007，25（2）：79－82.

［2］ 段新宇，缪立新，江见鲸.由路段交通流量反估出行OD矩阵技术的应用［J］.清华大学学报，2000，40（6）：123－126.

［3］ 夏志浩，王胜奎.用公交车站上下客数推算公交OD分布的方法［J］.四川联合大学学报：工程科学版，1997，1（2）：42－48.

［4］ 王济儒，查伟雄，李剑.由车站上下车客流量估计铁路OD矩阵［J］.交通运输工程与信息学报，2004，2（4）：23－27.

［5］ 林勇，蔡远利，黄永宣.基于广义最小二乘模型的动态交通OD矩阵估计［J］.系统工程理论与实践，2004（1）：136－140.

［6］ 周和平，晏克非，胡列格.基于随机模拟的遗传算法在OD反推中的应用研究［J］.系统工程，2003，21（4）：114－118.

［7］ CREMER M，KELLER H.A new class of dynamic methods for the identification of origin－destination flows［J］.Transportation Research Part B：Methodological，1987，21（2）：117－132.