多模盲均衡算法剩余码间干扰的近似表达式

王 成,杨 宾

(解放军信息工程大学信息系统工程学院,河南郑州 450002)

多模盲均衡算法剩余码间干扰的近似表达式

王 成,杨 宾

(解放军信息工程大学信息系统工程学院,河南郑州 450002)

给出了多模自适应盲均衡算法所能达到剩余码间干扰的近似表达式,该表达式是关于迭代步长、均衡器阶数、输入信号统计量、信噪比和信道能量的函数.经仿真验证,该近似表达式较准确地反映了剩余码间干扰与均衡时各参数的数值关系.式中的信道能量和信噪比可以通过算法估计或实际测量获得,因此,新表达式在一定程度上可以代替仿真的方法,用来设计均衡器所需的自适应步长和阶数以及比较不同盲均衡算法的性能.

自适应盲均衡;多模算法;码间干扰表达式

在实际通信中,通信带宽受限和多径效应会导致接收端的不同码元在当前时刻出现重叠,即通常所说的码间干扰(Inter Symbol Interference,ISI)现象.码间干扰严重地影响了通信质量,限制了通信的最大传输速率.通常的解决方法是在接收端采用均衡技术.盲均衡技术能够在不降低通信有效带宽的同时完成信道均衡,是近年来数字通信领域的研究热点之一.

在当前主流的盲均衡算法中,Bussgang类算法由于计算量小、实现简单而得到了广泛应用.它依据信号的统计特征构建代价函数[1],一般配合最小均方误差(Least Mean Square,LMS)自适应算法最小化代价函数,调节均衡器权值.其代表有恒模算法(Constant Modulus Algorithm,CMA)和适用于高阶QAM信号的多模算法(MultiModulus Algorithm,MMA).

一段时间以来,有关盲均衡器收敛性能的研究主要集中在各算法的全局收敛性上[2-4],对收敛后的稳态性能讨论较少.均衡器的迭代步长、均衡器阶数等参数的选择往往需要大量仿真.近期,Pinchas等[5-7]提出了Bussgang类盲均衡算法收敛后所能达到剩余码间干扰的近似表达式.该理论从最小均方误差算法迭代方程出发,通过对代价函数的多项式展开,得到了剩余码间干扰与迭代步长、均衡器阶数、输入信号统计量和信噪比的关系.然而该理论仅限于使用某单一代价函数的算法,对于多模算法这类需依据输入数据实时选择代价函数的情况无法适用,这限制了该理论的实际应用.

在Pinchas等人理论的基础上,笔者通过对不同代价函数参与最小均方误差算法迭代所产生影响的分析,修正了剩余码间干扰计算公式.改进公式不仅能够准确计算多模算法的剩余码间干扰,也同样适用于各种常见的Bussgang算法.

1 系统模型

数字通信系统的基带模型如图1所示,其中s(n)为零均值的独立同分布信源符号;h(n)表示传输信道的冲激响应,这里假设h(n)没有在单位圆附近的零点,即非深衰落信道;w(n)是加性高斯白噪声;x(n)表示可观测的接收信号;c(n)表示均衡器系数;y(n)表示均衡器输出信号.

图1 通信系统基带模型示意图

均衡的目的是消除信道的影响.用符号“*”表示卷积操作,信道与均衡器联合响应用β(n)表示,则理想均衡时,有[1]

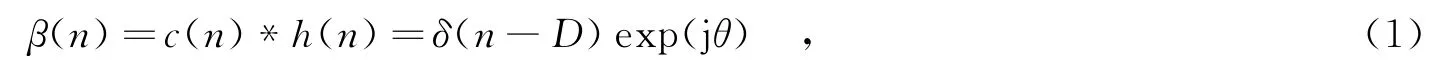
其中,D表示固有延时;θ表示相偏.理想均衡一般难以实现.设均衡器系数与理想均衡器系数的误差用ξ(n)表示,则有如下关系:

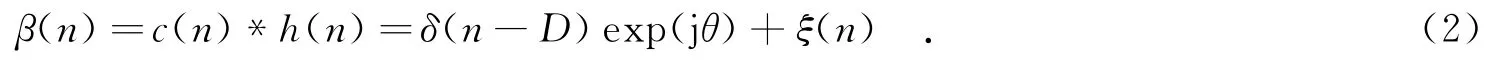
为方便讨论,在不影响分析的前提下,设D=0,θ=0.定义卷积噪声p(n)=s(n)*ξ(n),则均衡器输出可表示为

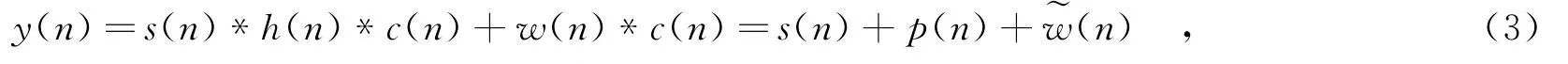
其中,˜w(n)为加性高斯白噪声对应的均衡器输出,˜w(n)=w(n)*c(n).均衡算法的性能一般由剩余码间干扰来衡量,它由联合冲击响应定义:

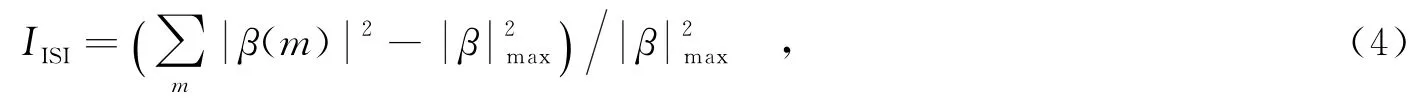
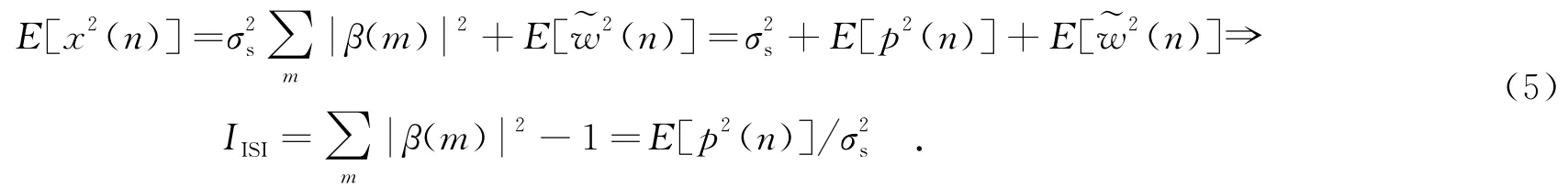
由式(5)可知,码间干扰是卷积噪声的二阶矩E[p2(n)]与信号方差之比.已知发送信号的调制类型即可确定所以如果能定量表示卷积噪声的二阶矩,则可得到相应剩余码间干扰的表达式.

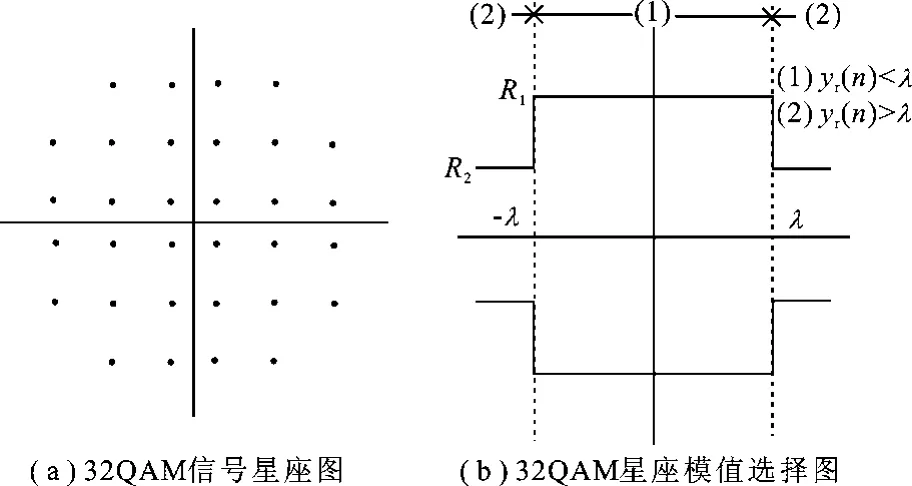
图2 32QAM信号多模算法模值选取示意图

2 多模盲均衡算法

为充分利用QAM信号星座的符号统计信息,完成均衡,Yang等[8]提出了对分属不同区域的信号样点,采用不同模值的多模算法.以32QAM信号为例,假设其实部、虚部电平值由{±1,±3,±5}组成.从图2(a)中可以看出,符号实部与虚部不同电平值出现概率不同.基于上述特性,多模算法将32QAM信号实部和虚部的取值依门限λ划分为两个区域,分别取模值R1与R2,如图2(b)所示.由此得到代价函数

其中,λ为与信号星座有关的常数,不同区域模值由该区域内星座点的统计平均得到.对于信号星座点数更高的情况,多模算法需要划分更多子区域.

用“()*”表示取共轭,“()T”表示转置运算.设n时刻对应于实部和虚部的均衡器系数向量分别为和i(n).L表示均衡器阶数;输入向量和xi(n)分别为的实部和虚部;μ表示最小均方误差算法迭代的步长.多模算法迭代公式如下[8]:

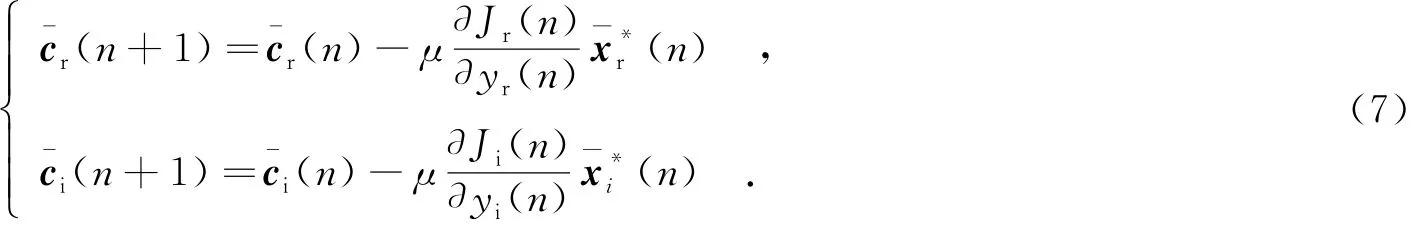
多模算法能纠正相位偏转,尤其适用于处理高阶QAM信号[9],再加上算法本身计算量小,能处理非最小相位系统,所以受到了研究者的广泛关注.

3 多模算法剩余码间干扰表达式

文献[7]从最小均方误差算法迭代方程出发,利用代价函数的多项式展开,得到了卷积噪声方差与均衡器各参数间的统计关系,进而得到了均衡后码间干扰的表达式.然而,由于仅考虑了单一代价函数的情况,其结论对于如多模算法这类需依据输入数据实时选择代价函数的情况无法适用.文献[7]已证明对于单一代价函数的盲均衡算法,卷积噪声实部pr有如下关系成立:

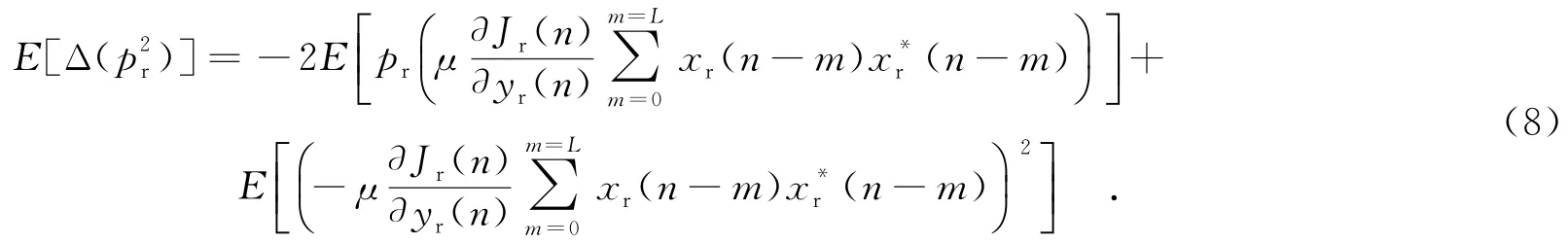
在此基础上讨论多代价函数的情形.考虑多代价函数时,算法依据均衡输出的范围不同,采用不同代价函数.因此,各代价函数Jk对卷积噪声的影响应服从信号样点的概率分布.用φ代表概率,信源符号中子集sr,k出现的概率为φ(sr,k),则有

假设有K组代价函数,将式(8)修正为如下形式:

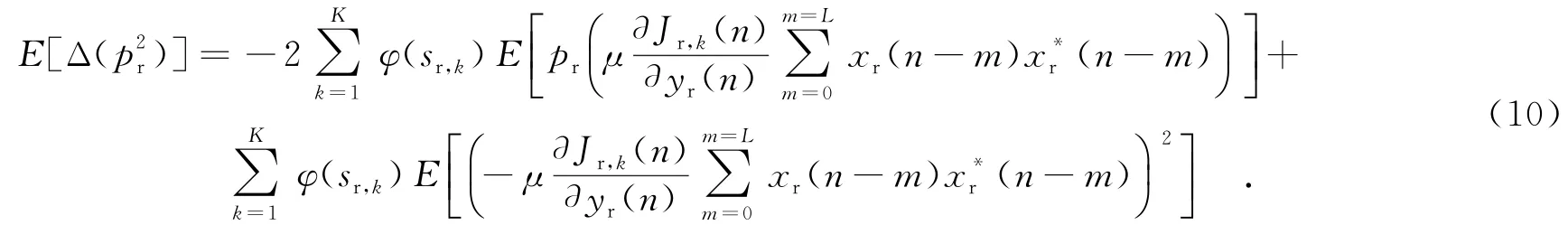
值得注意的是,虽然不同时刻输入向量xr对应恢复出的符号sr,k不同,但xr本身是由信源符号序列卷积信道所得的.所以,即使对应不同的代价函数Jk,各时刻均衡器输入向量的统计特性仍完全一致,都满足

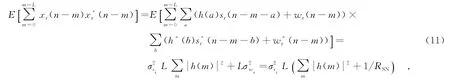
其中,ai为代价函数各展开项系数.特别地,对多模算法,a1=-Rk,a12=0,a3=1.多模算法区域划分确定后,各区域的模值Rk即可由该区域内星座点模值统计平均得到.式(11)中信道能量和信噪比可以通过算法估计或实际测量获得.均衡器收敛后,有因此给定步长μ和均衡器阶数L,就可以通过解式(10)的方程计算

用mp代指由于收敛后mp数值较小,可以忽略其三次及三次以上的项.将式(11)和式(12)代入式(10),经化简,最终mp是如下二次方程较小的正解:

笔者给出的剩余码间干扰的改进计算公式并不局限于多模算法这类实时选择代价的情况,其思路也适用于其他联合采用多代价函数的盲均衡算法.处理其他算法时,仍按上述思路,首先计算各代价函数的使用概率或对卷积噪声的影响比例,然后将其多项式展开代入式(10),即可获得相应算法的剩余码间干扰表达式.另外,当算法仅有单一代价函数时,φ(J=Jk)=1.笔者推导的公式与文献[7]中的基本一致,所以后者可以看做是笔者给出算法的特例.

4 仿 真

下面用仿真验证多模算法剩余码间干扰表达式的准确性.计算机仿真选用文献[10]中以下两种信道:

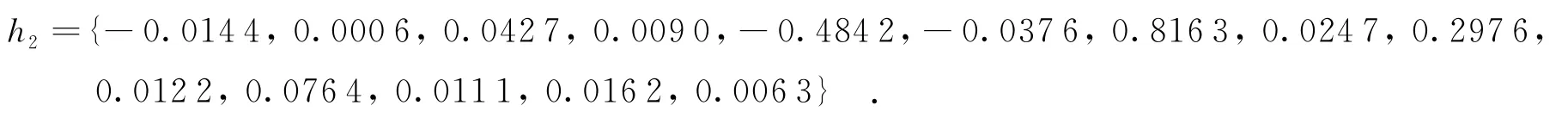
首先选用32QAM信号进行仿真验证.式(6)中判决门限λ=4,代价R1使用的概率为2/3,sr,1∈(±1,±3,±5);代价R2使用的概率为1/3,sr,2∈(±1,±3).图3比较了不同步长和均衡器阶数下,多模算法均衡32QAM信号所得到的实际码间干扰收敛曲线与理论码间干扰值,信噪比为20 dB.

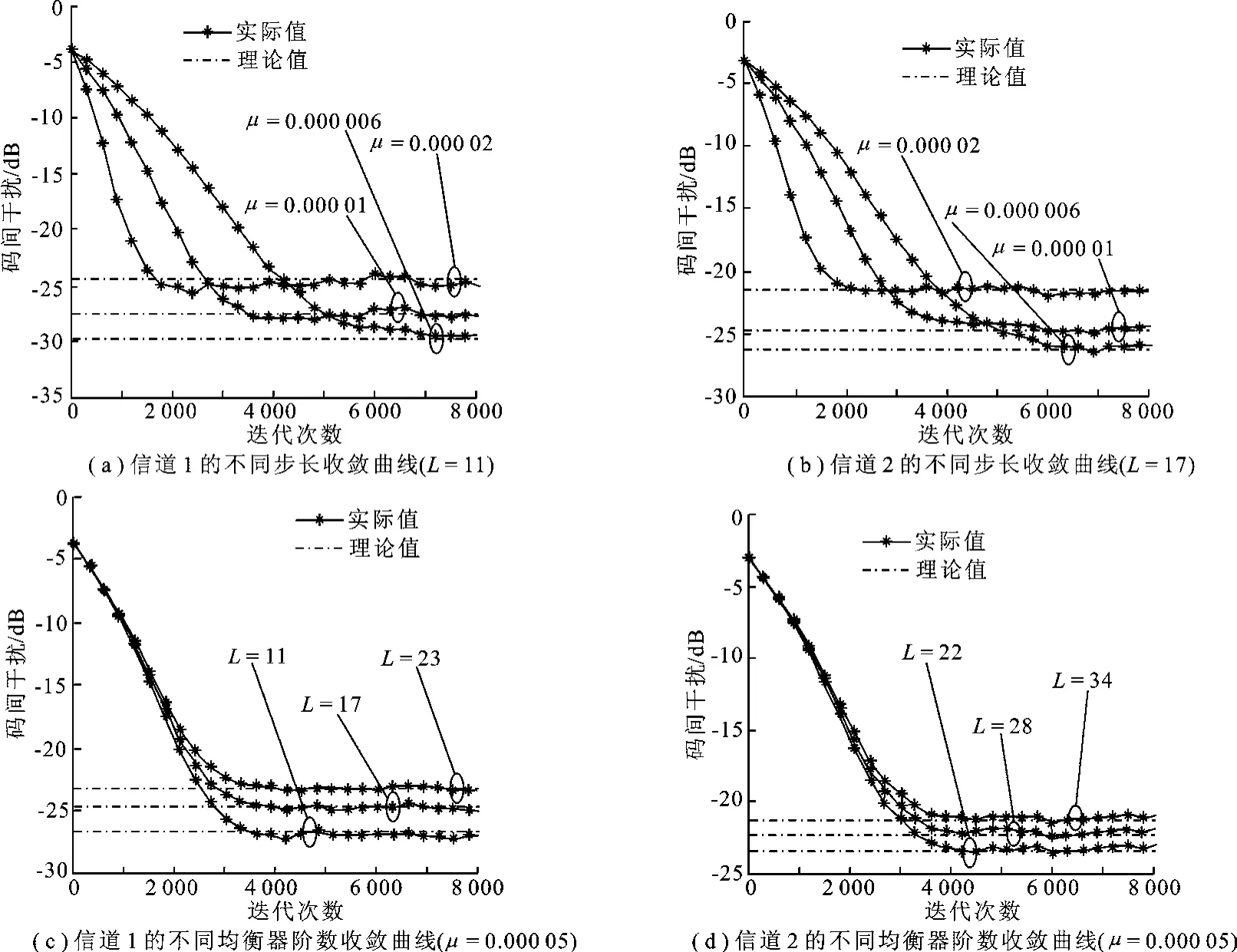
图3 32QAM信号收敛曲线示意图

如图3所示,实际码间干扰随步长和均衡器阶数L增大而增大,随其减小而减小,理论值也随之变化,两者数值大小基本一致.对式(14)定性分析也不难发现理论值变化的规律,步长μ或阶数L的改变,导致项随之变化,对应于二次方程常数项的变化.二次方程一般有两根,但这里卷积噪声对应于绝对值很小的根,会决定常数项大小,所以由近似表达式计算出的码间干扰值会随步长和均衡器阶数的增大而增大,并随其减小而减小.

下面选用256QAM信号.多模算法将星座划分为3个区域:当yi＞12时,使用代价R1=14.18,使用概率为1/4,sr,1∈(±13,±15);当8＜yi＜12时,使用代价R2=10.25,使用概率为1/4,sr,2∈(±9,±11);当yi＜8时,使用代价R3=6.07,使用概率为1/2,sr,3∈(±1,±3,±5,±7).图4比较了不同步长和均衡器阶数下,多模算法均衡256QAM信号所得到的实际码间干扰收敛曲线与理论码间干扰值,信噪比为20 dB.可以看出,预测值与理论值基本一致.

5 结束语

针对多模算法类的算法,笔者给出了采用多代价函数的自适应盲均衡算法所能达到剩余码间干扰的近似表达式.在原有理论的基础上,通过分析多代价函数参与最小均方误差算法迭代的影响,得到了码间干扰关于迭代步长、均衡器阶数、输入信号统计量、信道能量以及信噪比的函数.经仿真,新表达式较准确地反映了码间干扰与均衡时各参数的数值关系.在实际均衡处理时,迭代步长、信源统计量和均衡器阶数都是已知的,信道能量和信噪比可以通过算法估计或实际测量获得,所以该表达式可以用来直接估计均衡所需的最佳参数,比较不同盲均衡算法的性能,避免了传统的数据仿真环节所需的大量计算.笔者提出的改进公式适用于各种Bussgang类盲均衡算法,具有广泛的应用前景.

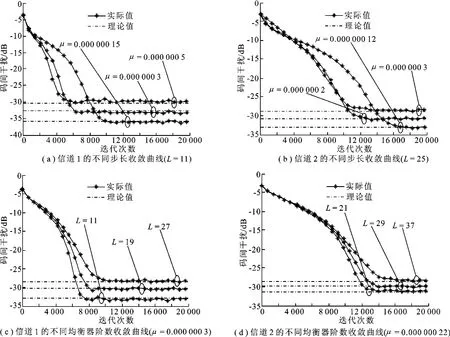
图4 256QAM信号收敛曲线示意图

[1]Haykin S.Adaptive Filter Theory[M].Fourth Edition.Englewood Cliffs:Prentice Hall,2002:772-790.

[2]LeBlanc J P,Fijalkow I,Johnson C R Jr.CMA Fractionally Spaced Equalizers:Stationary Points and Stability under IID and Temporally Correlated Sources[J].International Journal of Adaptive Control and Signal Processing,1998,12(2):135-155.

[3]Sharma V,Raj V N.Convergence and Performance Analysis of Godard Family and Multimodulus Algorithms for Blind Equalization[J].IEEE Transactions on Signal Processing,2005,53(4):1520-1533.

[4]Yuan J T,Lin T C.Equalization and Carrier Phase Recovery of CMA and MMA in Blind Adaptive Receivers[J].IEEE Transactions on Signal Processing,2010,58(6):3206-3217.

[5]Pinchas M.A Closed Approximated formed Expression for the Achievable Residual Intersymbol Interference obtained by Blind Equalizers[J].Signal Processing,2010,90(6):1940-1962.

[6]Pinchas M.A New Closed Approximated Formed Expression for the Achievable Residual Intersymbol Interference Obtained by Blind Equalizers for Noisy Case[C]//Proceedings-2010 IEEE International Conference on Wireless Communications,Networking and Information Security.Piscataway:IEEE,2010:26-30.

[7]Pinchas M.A Novel Expression for the Achievable MSE Performance Obtained by Blind Adaptive Equalizers[J].Signal,Image and Video Processing,2013,7(1):67-74.

[8]Yang J,Werner J,Dumont G A.The Multimodulus Blind Equalization and Its Generalized Algorithms[J].IEEE Journal on Selected Areas in Communications,2002,20(5):997-1015.

[9]Li X L,Zeng W J.Performance Analysis and Adaptive Newton Algorithms of Multimodulus Blind Equalization Criterion [J].Signal Processing,2009,89(11):2263-2273.

[10]Pinchas M.A MSE Optimized Polynomial Equalizer for 16QAM and 64QAM Constellation[J].Signal,Image and Video Processing,2011,5(1):29-37.

(编辑:郭 华)

Approximated expression for the achievable residual intersymbol interference obtained by multimodulus blind equalizers

WANG Cheng,YANG Bin
(Institute of Information System Engineering,PLA Information Engineering Univ.,Zhengzhou 450002,China)

A closed approximated formed expression for the achievable residual inter-symbol interference(ISI)is proposed for the adaptive equalizers that adopt the multimodulus algorithm.The expression depends on the step-size parameter,equalizer’s tap length,input signal statistics,signal noise ratio and channel power.Simulation proves that the expression shows the exact relationship between residual intersymbol interference and involved parameters.Since the channel power and signal noise ratio of the expression are measurable or can be calculated,this new approximated expression can be a useful tool for choosing the step-size and tap length for designing an equalizer,and for making direct performance comparison between blind equalizers based on distinct algorithms.

adaptive blind equalization;multimodulus algorithm;expression of inter symbol interference

TN929.5

A

1001-2400(2014)01-0176-06

10.3969/j.issn.1001-2400.2014.01.031

2012-11-01 < class="emphasis_bold">网络出版时间:

时间:2013-09-16

国家高技术研究发展计划资助项目(2009AA011504)

王 成(1988-),男,解放军信息工程大学硕士研究生,E-mail:melody198819@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.218_027.html