2n周期优秀二元序列生成及其特性分析

牛志华,李 政,李 哲,辛明军

(上海大学计算机工程与科学学院,上海 200444)

2n周期优秀二元序列生成及其特性分析

牛志华,李 政,李 哲,辛明军

(上海大学计算机工程与科学学院,上海 200444)

定义周期为2n的线性复杂度和k错线性复杂度均高的二元序列为优秀序列,设计了遗传算法来生成2n周期优秀二元序列.对周期为8、16、32,k值为N/4的情况,匹配各种参数搜索优秀序列,用Lauder-Paterson算法对得到的结果序列的线性复杂度谱进行了分析,以说明它们确实是优秀序列.由实验结果推测周期N为2n的二元优秀序列当k取N/4、N/8时的k错线性复杂度满足规律LCk(S)≤N-2k+1(对周期为64、128、256的序列也进行了实验验证),并且优秀序列在所有同周期的二元序列中所占的比例为1/4.

流密码;周期序列;线性复杂度;k错线性复杂度

设(S)=(s0,s1,s2,…)是有限域GF(q)上的序列,若对于任意的i,有si=si+N,则称(S)为N周期序列.称(S)满足的下列线性递归关系式的最小的阶数为序列的线性复杂度,记为LC(S):

密钥流序列的线性复杂度必须足够大,因为只要知道连续2LC(S)个比特,就可以通过解线性方程组或借助BM算法[1]将整个序列完全确定.

密钥流序列不仅应该具有高的线性复杂度,而且其线性复杂度必须稳定.例如一个周期为N的二元序列(S)=(0,0,…,0,1)∞,其线性复杂度LC(S)为N,但只要把其每一周期的最后一位的1变为0,该序列的线性复杂度就立刻降为0,这样的序列是不稳定的,显然,用来作为密钥流序列是不安全的.针对这一问题,国内外学者相继提出了球体复杂度、重量复杂度[2]、k错线性复杂度[3]的概念.后来,人们更习惯用k错线性复杂度的概念来描述线性复杂度的稳定性.

设(S)是有限域GF(q)上周期为N的序列,当改变(S)的周期中至多k(0≤k≤N)位后,得到的所有序列的线性复杂度中最小的线性复杂度称为(S)的k错线性复杂度,记为LCk(S),即LCk(S)=,这里(E)是周期为N的序列,WN(EN)表示(E)的周期中不为零的元素个数.

笔者研究2n周期二元序列,对于该周期序列,Games-Chan[4]和Stamp-Martin[3]分别给出了其线性复杂度和k错线性复杂度的快速算法,结合Games-Chan算法和Stamp-Martin算法,Lauder-Paterson[5]提出了线性复杂度谱算法.该周期序列的理论分析文章见文献[6-7].

综上,密钥流序列不仅应该具有高的线性复杂度,而且应该具有高的k错线性复杂度(对于不太大的k),传统的序列生成方法(例如割圆序列、交错序列等)能够生成线性复杂度较高的序列,但是无法同时兼顾到线性复杂度的稳定性.遗传算法是基于自然界中不必明确地描述问题的全部特征,只需要根据自然法则来产生新的更好解的这种思想而发展起来的一种通用的问题求解方法,具有极强的鲁棒性.笔者首先设计遗传算法来生成线性复杂度和k错线性复杂度都高的优秀序列,然后分析优秀序列的特性.

1 生成二元优秀序列的遗传算法设计

首先给出文中用到的定义和引理如下:

定义1 同时具有高的线性复杂度和高的k错线性复杂度的序列称为优秀序列,如果线性复杂度和k错线性复杂度都达到了可能的最大值,则称该序列为最优序列.

给出优秀序列的定义是为了文中叙述方便,这里的优秀仅指线性复杂度及其稳定性意义上的优秀,不考虑序列评价的其他指标.

定义2 设(S)是GF(q)上的周期序列,定义minerror(S)为满足LCk(S)＜LC(S)的最小的k值,即minerror(S)是满足LC(S+E)＜LC(S)的错误向量EN的最小汉明重量[6].

引理1 对于2n周期二元序列,如果LC(S)≥3,则LCminerror(S)≤LC(S)-3[7].

下面设计生成二元优秀序列的遗传算法.

笔者所设计的遗传算法的主要思想为首先按照种群规模随机生成一定数量的序列组成初始种群,然后利用设计的算法计算其适应度,通过遗传算子的操作迭代选择出最优个体.具体设计如下:

算法的输入是一定数目的序列,输出是得到的优秀序列.由于遗传算法依赖于它的一些参数,这里参数说明如下:PS表示种群规模,整数;GEN表示进化代数,整数;p X表示交叉概率,[0,1]区间的一个值;p M表示变异概率,[0,1]区间的一个值.

(1)编码方式 在标准遗传算法中,通常采用二进制编码方法.二进制编码方法与生物染色体的组成较类似,便于从遗传学的角度来解释,并且遗传操作如交叉、变异比较容易实现,算法处理的模式最多.二进制编码方法产生新个体的可能情况多,且产生的新个体不受父代个体所构成的种群的限制,因此二进制编码方法搜索能力比其它的编码方法强.由于处理的序列本身为二元序列,故直接采用序列本身作为染色体进行遗传操作.

(2)初始种群 对于给定的N,随机生成PS个长为N的二元序列作为遗传算法的初始种群.

(3)适应度函数的设计 根据优秀序列的定义,最终得到的个体为种群中线性复杂度和k错线性复杂度较高的个体,故需计算序列的线性复杂度和k错线性复杂度值的和.序列的线性复杂度和k错线性复杂度的和越高,在种群生成中个体的适应度也越高,此序列被选择复制的概率也越大,搜索得到优秀序列的几率亦越大.笔者采用Games-Chan算法[4]来计算周期为2n的二元序列的线性复杂度,采用Stamp-Martin算法[3]来计算周期为2n的二元序列的k错线性复杂度,将两者的和作为适应度函数.

(4)选择操作 采用轮盘选择算法做选择操作.选择的过程为在N次轮盘旋转的过程中,每一次旋转选择一个染色体,然后将选出的染色体组成新的种群.

(5)交叉操作 采用单点交叉方法(SPX).产生一个随机的自然数r,满足0≤r＜N.按如下方式交叉两个选中的序列.

交叉前的初始序列为

交叉后的序列为

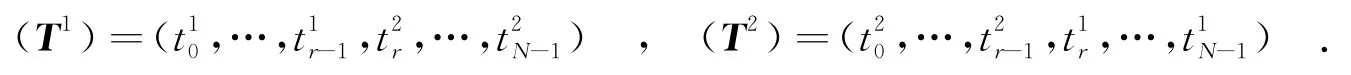
(6)变异操作 遗传算法中,变异操作是必要的.变异亦称为突变,就是改变染色体某个(些)位上的基因.通过遗传操作,可以引入新的基因,从而容易得到良好的个体.

2 二元优秀序列的特性分析

本节的实验分为3部分:第1部分为基于上节设计的遗传算法得到周期为N的二元优秀序列,第2部分为基于遗传算法来得出2n周期二元优秀序列的k错线性复杂度规律,第3部分为通过穷举法得到优秀序列在所有同样周期的二元序列中所占的比例.

2.1 基于遗传算法得到周期为N的二元优秀序列

用上节设计的遗传算法进行试验,实验首先考虑周期N为8、16、32,k值为N/4,使用种群规模、迭代代数、交叉率、变异率等参数的常用范围进行各种组合的匹配,从而使遗传算法的搜索结果更加全面,将搜索得到的结果序列用Lauder-Paterson算法[5]计算其线性复杂度谱,由谱线分布的均匀程度来判断搜索的序列是否为线性复杂度和k错线性复杂度均较高的优秀序列.实验结果如表1～3所示.

表1 各参数组合得到的周期为8的二元优秀序列及Lauder-Paterson算法结果

表2 各参数组合得到的周期为16的二元优秀序列及Lauder-Paterson算法结果

显然,当周期为N时,线性复杂度LC(S)的最大值为N.由引理1,当N=8时,LCminerror(S)的最大可能值为5;当N=16时,LCminerror(S)的最大可能值为13;当N=32时,LCminerror(S)的最大可能值为29.根据表1～3的实验结果,通过遗传算法搜索得到的序列大部分达到了线性复杂度和最小错线性复杂度可能的最大值,并且由Lauder-Paterson算法计算得到的结果序列的线性复杂度谱线分布平稳,而且在不同的参数组合下得到的这些序列的谱线非常接近,所以说笔者设计的遗传算法能够得到优秀序列,并且得到最优序列的概率超过了50%.

表3 各参数组合得到的周期为32的二元优秀序列及Lauder-Paterson算法结果

2.2 2n周期二元优秀序列的k错线性复杂度规律

由2.1节中实验数据分析可得周期为N=2n的二元优秀序列的N/4错线性复杂度满足:

当N=8,k=N/4时,LS2(S)=5=8-2k+1;

当N=16,k=N/4时,LS4(S)=9=16-2k+1;当N=16,k=N/8时,LS2(S)=13=16-2k+1;

当N=32,k=N/4时,LS8(S)=17=32-2k+1;当N=32,k=N/8时,LS4(S)=25=32-2k+1;

因此,有下面的推测:

推测1 对于周期为N=2n的二元序列,当k=N/4、N/8时,其k错线性复杂度满足LCk(S)≤N-2k+1,并且该上界是可以达到的.

接下来对N=64,128,256的周期序列再用第二节设计的遗传算法进行实验验证,生成的优秀序列的N/4和N/8的错线性复杂度都不超过推测1给出的最大值,并且很多情况下能够达到该最大值,统计数据如表4所示.

表4 周期为N的二元周期序列的N/4和N/8的错线性复杂度最大值

2.3 二元优秀序列在同样周期的二元序列中所占的比例

由2.1节遗传算法搜索3个周期的序列所得到的数据可知,一部分的参数组合,均能得到线性复杂度和N/4错线性复杂度较高的优秀序列.由于遗传算法的搜索是由各种参数引导搜索的,对参数的设定依赖性较强.如果优秀序列在所有序列中所占比例很小,则不可能出现较多的参数组合均能搜索到良好的个体,故可知,优秀序列在所有同样周期的二元序列中会占一定的比例.所以有下面的大胆推测,并在N=8,16,32的情况下验证了该推测的正确性.

表5 周期为N的二元优秀序列在序列总数中的比例

推测2 对于周期为N=2n的二元序列,当k=2i时,使得线性复杂度和k错线性复杂度都达到可能的最大值的优秀序列所占的比例为1/4.

以达到LS(S)=N,LSk(S)=N-2k+1的序列为优秀序列,对周期为N=8、16、32的所有序列进行了穷举验证,得到的数据如表5所示.

表5不仅说明了推测2的可能性,而且在这个过程中没有发现不满足推测1的序列,也说明了推测1的合理性.当N=64时,要通过穷举来验证推测2由于计算规模过大而不可行.

3 结束语

密码学上强的序列不仅应该具有高的线性复杂度,而且应该具有高的k错线性复杂度,传统的序列生成方法(例如割圆序列,交错序列等)以生成线性复杂度高的序列为目标,然后再分析所生成的序列的k错线性复杂度,往往k错线性复杂度的分析非常困难.笔者基于遗传算法的鲁棒性和它在多目标优化中的优势,以线性复杂度和k错线性复杂度的和为适应度函数引导搜索找到线性复杂度和k错线性复杂度都高的优秀序列;在搜索过程中发现了2n周期序列的k错线性复杂度的一些规律和最优序列的分布情况,并对此进行了大胆的推测;然后通过大量的实验对推测进行了验证,当周期为32时,验证工作就需要大量的时间,对更长的周期进行实验验证基本不可行.所以寻求理论上的证明将是下一步努力的方向.

[1]Berlekamp E R.Algebraic Coding Theory[M].New York:McGraw-Hill,1968.

[2]Ding C,Xiao G,Shan W.The Stability of Stream Cipher[M].Lecture Notes in Computer Science:561.Berlin: Springer,1991.

[3]Stamp M,Martin C F.An Algorithm for the k-error Linear Complexity of Binary Sequences with Period 2n[J].IEEE Transactions on Information Theory,1993,39(4):1398-1401.

[4]Games R A,Chan A H.A Fast Algorithm for Determining the Complexity of a Binary Sequence with Period 2n[J].IEEE Transactions on Information Theory,1983,29(1):144-146.

[5]Lauder A G B,Paterson K G.Computing the Error Linear Complexity Spectrum of a Binary Sequence of Period 2n[J]. IEEE Transactions on Information Theory,2003,49(1):273-280.

[6]Kurosawa K,Sato F,Sakata T,et al.A Relationship Between Linear Complexity and k-Error Linear Complexity[J]. IEEE Transactions on Information Theory,2000,46(2):694-698.

[7]Chang Z,Wen Q,Chang Z,et al.On Cryptographic Properties of Binary 2n-periodic Sequences[J].Chinese Journal of Electronics,2011,2(2):307-311.

(编辑:李恩科)

Generation and analysis of the excellent 2n-periodic binary sequences

NIU Zhihua,LI Zheng,LI Zhe,XIN Mingjun
(School of Computer Engineering and Science,Shanghai Univ.,Shanghai 200444,China)

The 2n-periodic binary sequence with high linear complexity and high k-error linear complexity is defined as an excellent sequence.We design a genetic algorithm for generating excellent sequences and studying their features.Choosing the N-periodic binary sequences,where N=8,16,32,k=N/4,we search the resulted sequences by the genetic algorithm with various parameters,and compute the linear complexity profiles of results sequences by using the Lauder-Paterson algorithm,to confirm that the obtained sequences are the real excellent sequences.By numerous experiments,we speculate that the kerror linear complexity of the N-periodic binary excellent sequence meets the formula LCk(S)≤N-2k+1,when k=N/4、N/8(we also do experiments on sequences with periods 64,128 and 256).By the brute-force method we obtain that the proportion of the excellent sequence in all binary sequences of the same period is 1/4.

stream cipher;periodic sequence;linear complexity;k-error linear complexity

TN918.4

A

1001-2400(2014)01-0130-05

10.3969/j.issn.1001-2400.2014.01.023

2012-11-07 < class="emphasis_bold">网络出版时间:

时间:2013-09-16

国家自然科学基金资助项目(60903187,61074135,61272096,61202395);上海市自然科学基金资助项目(13ZR141610);教育部新世纪优秀人才支持计划资助项目(ncet-12-0620)

牛志华(1976-),女,副教授,博士,E-mail:zhihua_niu@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20130916.0926.201401.162_019.html