Activation Pattern of Nuclear Factor-kB in Skin after Mechanical Stretch–a Multiscale Modeling Approach

V.B.Shimand K.Mithraratne

1 Introduction

Skin is the outermost tissue of the body and the largest organ in terms of surface area.It has a very complex structure that consists of many components.Cells,fibres and other components make up several different layers that give skin a multilayered structure.Human skin is comprised of three layers:the epidermis,dermis and subcutaneous fat.The melanocyte cells in the basal layer of the epidermis produce melanin.The skin colour is primarily determined by the amount of melanin,which also provides protection against the effects of the sun such as cutaneous melanoma and premature aging.

Melanoma progresses from pigmented lesions.Further progression leads to an insitu melanoma,which grows laterally and is primarily confined to the epidermis.This stage is known as radial growth phase(RGP)of melanoma.If left untreated,it can progress to the vertical growth phase(VGP),which is associated with invasion of the dermis by melanoma cells.The activation of nuclear factor kappa B(NF-kB)has been suggested as an event that triggers melanoma progression[Huang et al.(2000)].NF-kB is a protein complex found in almost all animal cell types and known to be involved in cellular responses to stress stimuli.

Mechanical behaviour of skin has been extensively studied and a number of computational models to study its constitutive properties and predict deformation under varying load conditions have been reported in the literature.Most mechanical models looked at macro level mechanics employing either theory of linear elasticity or finite deformation(non-linear)elasticity to describe strain-displacement kinematic relationships[Bischoff et al.(2000);Flynn and McCormack(2010);Hendriks et al.(2003)].However,the relationship between mechanical behaviour and the activation of NF-kB in skin has not been investigated.The aim of this study is to use a multiscale finite element model of the skin to analyse the activation pattern of NF-kB in skin under mechanical stimulation.In particular,we aim to investigate the role of dermal epidermal junction in stress transfer within the tissue and subsequent activation of NF-kB in skin.Our hypothesis is the flattening of dermal-epidermal junction in skin due to aging[Sauermann et al.(2002)]will lead to increased activation of NF-kB in skin,leaving the tissue prone to develop melanoma.

2 Methods

2.1 Overall modeling framework

Our multiscale modeling framework is composed of three levels–macro,meso and cell levels.The macro level model simulates active contraction of the Zygomaticus major in the face.The micro FE model of the skin that includes accurate description of the layered structure of the skin and distribution of melanocytes is our meso level model,which is embedded inside the macro level model of the Zygomaticus major muscle.Therefore the deformation of the muscle due to contraction informs the micro FE model of the skin embedded in the muscle model.Finally the maximum principal strain values at the integration or Gauss points in the micro FE skin model inform the cell model,which is a system of ordinary differential equations that predicts the level of nitric oxide synthase,an inducible pro-inflammatory enzyme that corresponds to the level of activation of NF-kB signaling pathway.The links between macro,meso and cell level models were done using the multiscale computational framework developed by the Auckland Bioengineering Institute for the Physiome Project[Hunter and Borg(2003)].

2.2 Macro level:Active contraction of the Zygomaticus major in the face

A previously developed data fitting algorithm[Bradley et al.(1997)]was used to construct an anatomically based 3D geometry of a soft tissue block in the cheek area.Skin,the subcutaneous fat and muscles are embedded in this tissue block and the geometry was represented using a single tri-cubic-Hermite FE mesh(Figure.1).In fact,the same method has already been used to create the 3D meshes of other major organs and tissues to store them in a web-based open-source repository of models,which contributing scientists can easily use and disseminate their findings[Hunter et al.(2002)].In our study,the Zygomaticus major muscle(Figure.1b)was developed and embedded in the cheek tissue continuum(Figure.1a).The spatial data required to construct the mesh topologies using this fitting method were derived from the visible human anatomical sections[Ackerman(1998)].

Figure 1:3D cubic-Hermite finite element models(a)Cheek issue block with embedded muscle(b)Zygomaticus major muscle.

The fibre or fascicular orientation within the muscle volume is very important in active contraction mechanics as the force generated by sarcomeres act along the fibre direction.In order to depict the fibre directions accurately,an orthogonal curvilinear material coordinate system was defined such that its axis one follows the fibre direction.Furthermore,this material coordinate system naturally facilitates to define the constitutive properties of the muscle as most soft tissues exhibit transversely-isotropic behaviour.This was achieved by aligning the first material axis direction with finite element coordinate axis,.When constructing the finite element mesh of the muscle thedirection was defined along the length,circumferentially andin anterior-posterior direction of the muscle belly as shown in Figure1b.

A similar procedure was adopted to define the orthogonal curvilinear material coordinate system for cheek tissue block as well.Thus,at any given material point in the muscle,which is also a material point of the cheek tissue block as the muscle is completely embedded in the tissue block,one can obtain coordinate axis vectors for both coordinate systems.Using these directional vectors,three Euler angles were determined to align material coordinate system of the cheek tissue block with that of an embedded muscle(in the present case Zygomaticus major).

A uniformly spaced dense data cloud was created in the tissue block and the three Euler angles were determined at each point.For instance,if a point falls outside the muscle volume,the Euler angles are zero,otherwise there will be three non-zero angles.These angles were then fitted as a finite element field(similar to geometry fitting).Thus,at any given material point in the tissue block,the initial material vectors are calculated such that the first direction aligns with FE coordinate axis one.Then three sequential rotations are applied.The rotation angles are obtained by interpolating the nodal angle values.After these rotations the first material direction should align with muscle fibre direction at that point.The fibre organization in the tissue block due to the contribution of the Zygomaticus major is depicted in Figure 2.

Figure 2:Fibre organization in the tissue block.

The deformation of the soft tissue block in response to neural activation subject to prescribed boundary conditions can be obtained by solving the static Cauchy equation,

whereσijare Cauchy stress tensor components,xjare spatial coordinates,bjare body force components andρis the soft tissue density.

The weak form of the above governing equation was formulated using the method of weighted residuals and final FE model equations were obtained using the Galerkin FE method.The non-linear algebraic equations so derived were numerically solved using the Newton-Raphson method.Furthermore,body force vector,bjin eq.(1)was also neglected assuming the deformation caused by the gravity is insignificant.In order to account for the heterogeneity of the soft tissue continuum,the Gauss or the integration points of the tissue block were categorised into three groups to represent the skin,fat and muscle and assigned different constitutive properties.The mechanical behavior of all three soft tissue groups were modeled as isotropic hyper-elastic materials and described in the following form.

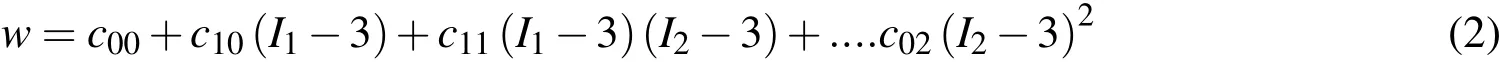
wherewis the strain energy density function(SEDF),I1andI2are first two principal invariants of the right Cauchy deformation tensor,C andc00,c10,etc.are experimentally determined constants.

Table 1 below gives the values used for the parameters in eq.(2).Fig.3 depicts the Gauss points belong to various groups.Furthermore,all soft tissue groups were modeled as incompressible materials and therefore eq.(2)was modified by appending a constraint via a Lagrange multiplier to account for incompressibility of the tissue as follows.

whereI3is the third principal invariant of C or square of the ratio between deformed and un-deformed volumes andpis the Lagrange multiplier,also known as the hydrostatic pressure.

Apart from the stress-strain or constitutive relationship of the material,boundary conditions are also required to solve eq.(1).Ideally,one would like to use physiologically realistic boundary conditions together with experimentally determined constitutive properties under controlled conditions to obtain accurate simulation results.

Table 1:Constitutive properties of the soft tissue continuum.

Figure 3:Assigning constitutive properties for tissue block.

Such physiologically realistic boundary conditions would include sliding of the inner surface of the soft tissue continuum over the maxilla and mandible bones(Figure.1a)as well.Sliding contact mechanics,however,will bring uncertainties into the computational model,as the friction coefficient between the soft tissue and bone in the face,is not currently known.Therefore,the interaction(sliding)between the soft tissue continuum and deep articular muscles/bony structures were not considered in the present model.Therefore nodes indicated as the‘boundary nodes’in Figure 3 are constrained and prescribed as displacement boundary conditions required for the solution of eq.(1).The closest node to the bony attachment site of the muscle(not shown in Figure 3)was also constrained as bony attachment sites,in general,are stationary during muscle contractions

The force generated by the contraction of muscle fibers upon stimulation is initiated by the release of Ca2+.Although the process of the Calcium binding to Troponin-C and resulting activation of muscle fibers is time dependent,a steady state model[Hunter(1995)]was used in the present study.This model describes the relationship between the active stress,Tfiber extension ratio,λand a non-dimensional parameter to represent level of activation,aas follows.

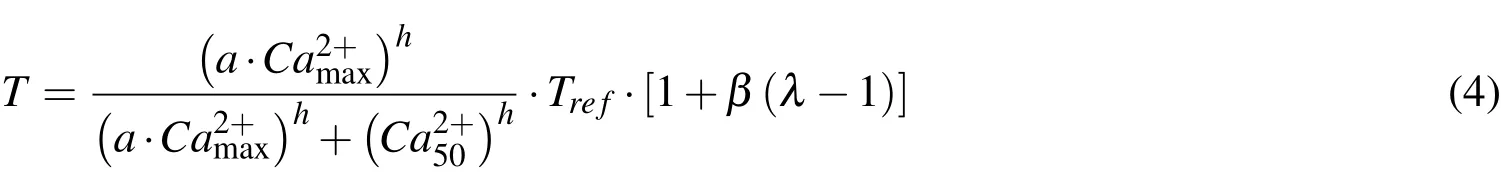
where(Ca2+)maxis the maximum intracellular calcium concentration,(Ca2+)50is the value corresponding to 50%of the maximum tensile stress,h is the Hill coefficient andβis the slope parameter.Trefrepresents the value atλ=1.0.

Once the active tensile stress in the fiber direction is determined from eq.(4),it is then converted to the corresponding second Piola-Kirchhoff(2PK)stress components and added to the passive 2PK stress tensor that was obtained by differentiating the SEDF(eq.(3))with respect to Green-Lagrange strain tensor.The active stress was evaluated only at the Gauss points inside the muscle volume marked as‘muscle’in Figure 3.The resulting muscle deformation informed the meso level skin micro FE model imbedded in the macro model.

2.3 Meso Level:Development of micro FE model of the skin

A detailed three-dimensional micro finite element model of skin was developed using the data derived from very high-resolution images.A skin sample(width:40mm,height 20mm,depth 15mm)was harvested from the cheek of a cadaver(78 yrs.,male)and fixed in paraffin wax.The sample was sectioned then to slices of 100µm thickness,creating total 30 slices that cover the thickness of the sample and stained with Fontana-Mason.Each slice had a number that identifies its location within the skin sample from which the slices were sectioned.Histologically stained slices were imaged with a light microscope(Nikon eclipse Ti)using 4x∼20x magnification lenses.Since the field of view(FOV)was too small to view the whole slice, we divided the slice into small sections and then image them separately.When the whole slice was imaged,image stitching was performed to create the complete view of the histological slices.Figure 4 shows this process.

The images were then digitised and reassembled as a 3D dataset to get the profile of surface microgeometry.A 3D finite element model composed of 1543 nodes and 896 elements were created with high order cubic Hermite basis functions to capture the complex shape of skin surface profiles.We then performed a non-linear fitting process where the data points in the 3D dataset are projected to the initial mesh and optimization is performed to minimize the distance between the data points and the mesh by deforming the mesh.

Figure 4:Collecting histological images with a light microscope.

Figure 5:Digitization of skin surface topology and geometric model generation.

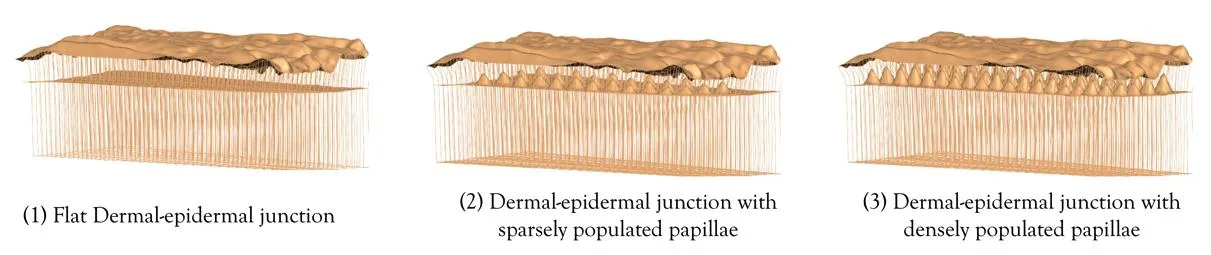
Figure 6:Parametric models for different levels of undulation of the dermalepidermal junction.

Once the finite element model representing the detailed surface geometry was created,the internal layered structure of the skin was incorporated.A similar approach used by Garcia-Martinez and Limbert[Garcia-Martinez and Limbert(2013)]was used where we parametrically modified the level of undulation of the dermalepidermal junction in skin.Three different cases were simulated–1) flat junction;2)sparsely populated papillae in the junction;3)densely populated papillae in the junction(Figure 6).

The finite element model so developed was then subject to Dirichlet boundary conditions to simulate deformation of the skin block due to activation of the Zygomaticus major.The deformed state of the skin block was obtained by solving the weak form of the governing equations,the static Cauchy equations using the Galerkin finite element method with non-linear kinematics.The material behaviour of the different layers in the skin–epidermal and dermal layers–was assumed to be nonlinear Neo-Hookean slightly compressible material model with the following strain energy density function[Tran et al.(2007)].

where I1is the first invariant of the strain tensor and J volumetric ration.The Neo-Hookean parameters C10and K were obtained from the material optimization study by Tran and colleagues[Tran et al.(2007)]and the values used are shown in Table 2.The top layer in the model was assigned with the epidermis properties while the bottom layer with the dermis property.The model was deformed according to the prescribed Dirichlet boundary condition from the macro level Zygomaticus major FE model and maximum principal strains at Gauss points within the model were computed to inform the cell level model for NF-kB pathways.

Table 2:Material parameters used for skin tissue block.

2.4 Cell Level:Development of cell models for NF-kB activation with mechanical stimulus.

We used the model developed by Nam et al.[Nam et al.(2009)],which is an updated version of the initial model developed by the Hoffmann group[Werner et al.(2005)]in that it incorporates the activation of IkB kinase(IKK)by mechanical stimuli.Therefore a mechanical signal controls nuclear localization of NF-kB and the subsequent expression of pro-inflammatory mediators such as nitric oxide synthase(NOS2).

This process was described with a set of twelve ordinary differential equations(ODE)that describe connections and dynamics between each step that lead to activation or inhibition of pro-inflammatory mediators.This set of ODEs was implemented using our open-source cellular modeling markup language called CellML and a software tool called OpenCOR(freely available for academic use at www.cell ml.org)[Shim et al.(2011)].The equations were solved using CVODE package for solving initial value problems for ODEs.CVODE uses Backward Differentiation Formula(BDF)method where the system of ODEs is solved using Newton iteration.Specifically,a Krylov method with preconditioned Generalized Minimal RESidual(GMRES)method was used[Saad and Schultz(1986)].

The cell level model was linked with the meso level skin FE model.The principal maximum strain values at Gauss points inside the skin FE model were passed onto the cell model that computed the level of NOS2 at steady state under the given mechanical stimulus.The activation level of NF-κB was expressed in terms of the level of NOS2 in the cytosol.The influence of the level of undulation in the dermal-epidermal junction on the activation of NF-κB was analyzed.

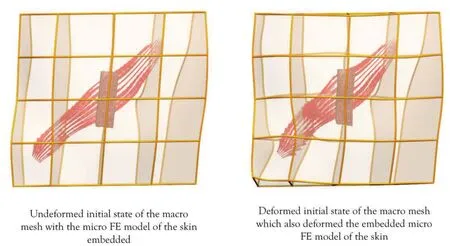
Figure 7:Deformation of the macro model and the subsequent deformation of the skin model embedded inside.

3 Results

3.1 Deformation of the Zygomaticus major under mechanical stretch

The FE simulations for both macro and micro level models were done using the software package CMISS[Bradley et al.(2011)]developed at the Auckland Bioengineering Institute.The contraction of the Zygomaticus major was simulated by increasing the level of activationain Equation 4 at Gauss points up to 0.8.The resulting active contraction of the muscle deformed the Zygomaticus major model as shown in Figure 7.The micro FE model of the skin was embedded in the centre of the macro model and deformed along with the macro model,resulting in non-homogeneous stretch of the skin block.

3.2 Activation of NF-kB in skin due to contraction of the Zygomaticus major

The strain distribution at the dermal-epidermal junction was highly dependent on the geometry of the junction.When the junction was either free from papillae or sparsely populated,the strain distribution was fairly homogeneous,displaying a low level of strain(Top row in Figure 8).However once the junction shape changes due to the increasing number of papillae,the strain distribution pattern became non-homogeneous and spatially varying.The activation pattern of NF-kB showed the characteristic step response as reported in the previous studies[Nam et al.(2009)].In the presence of inflammatory cytokines,the low level of strains at the flat junction activated NF-kB,resulting in almost uniform distribution of NF-kB in the whole junction.However,the presence of papillae in the junction changed the strain pattern,which also changed the activation pattern of NF-kB.Specifically,the papillae at the junction worked as an inhibitor of NF-kB when the tissue is mechanically stimulated as shown in Figure 8(bottom row).When the junction is densely populated with papillae,NF-kB was significantly inhibited throughout the junction.

4 Discussions

We have developed a multiscale model of skin that links a muscle in the face(the Zygomaticus major)to the skin surface microgeometry in the cheek to investigate the activation of NF-kB in the dermal-epidermal junction of the skin under mechanical stimulation.We used the multiscale framework developed as a part of the Physiome project,which is a web-based open-source repository of models,which contributing scientists can easily use and disseminate their findings[Christie et al.(2009)].

Figure 8:Strain distribution and subsequent activation of NF-kB patterns at the dermal-epidermal junction in skin.

Our results indicated that the deformation patterns of skin surface and inner layers were highly non-linear and dependent on topologies of both the skin surface and the dermal-epidermal junction.The resulting NF–kB activation patterns also showed high non-linearity,indicating that the geometry and the internal layer structure may play an important role in activation of this pathway.In particular,the flatting of the junction due to aging may play a role in prolonged activation of NF-kB in skin,which increases the likelihood of developing into melanoma.

There have been some previous works that investigated skin mechanics using computational approaches[Flynn and McCormack(2010);Hendriks et al.(2003);Bischoff et al.(2000)].However these works mainly dealt with the macro-scale mechanical properties and layered structures of skin and did not take into account of the cellular events occurring as a result of mechanical stimulation.In particular,the changes in the dermal-epidermal junction due to aging have been identified as a major factor that influences skin material properties and likelihood of injuries[Morey(2003)].But this has not been considered in the context of realistic physiological loading conditions,not to mention its implication on to the downstream cellular events.Therefore,to the authors’knowledge,the current work is the first attempt to link the macro level mechanical stimulation with cellular events within skin using a multiscale computational approach.

The current work has some limitations.First,the models at different scales were generated using different data sets.The Zygomaticus model was generated from the Visible Human data and the skin micro FE model was generated from a different human cadaver while the cell model was developed based on experimental data from human chondrocytes.The implication of using different subjects and cell types is not clear at this stage.However,our computational framework supports modular processes so when new and updated models become available,they can be switched with the existing models to investigate the effect of different tissue or cell types.Moreover,the current multiscale framework has been successfully used in investigating initiation of osteoarthritis in the knee[Shim et al.(2011)].Therefore,we are confident that our framework and the current results will shed important light in understanding the activation patterns of NF-kB.Another limitation is our use of an arbitrary activation pattern in deforming our macro level model of the Zygomaticus major.Ideally,the behaviour of NF-kB pathway under mechanical stimulation needs to be investigated with a number of different muscle activation patterns.However,although we used only one type of muscle activation in this study,the resulting mechanical stimulation on the skin block was a complex non-linear deformation that included tension,compression and shear.This gives us confidence in the capability of our model in predicting the cellular events in skin under physiological loading condition.Moreover,our future work includes embedding skin model inside various parts of human face to comprehensively analyse the activation of this important cellular pathway under various mechanical stimuli.The last limitation is the lack of model validation.In fact,it is a common problem that multiscale models usually have to face,as it is almost impossible to perform validation of any sort in multiscale modelling.However,the individual models used at different spatial scales have all been validated from our previous studies[Shim et al.(2008)]with different data set and a comprehensive model verification has been performed including mesh density and sensitivity analysis.Therefore,although a caution is required in interpreting the data,we are confident that our results will shed some important light in understanding the mechanism of melanoma,especially the role of mechanical stimulation.

In conclusion,we have presented a multiscale model capable of predicting NF-kB pathway activation at the dermal-epidermal junction in skin under mechanical stimulation.Our results indicate that the activation of this important pathway is highly dependent on the geometry of the junction and the type of mechanical stimulus.The future work will include expanding this model to the entire face to investigate the relationship in the melanoma development in the face and skin mechanical responses.

Acknowledgement:The work presented in this paper was funded by the Ministry of Business,Innovation and Employment of New Zealand under the grant number UOAX1006.

Ackerman,M.J.(1998):The Visible Human Project:a resource for anatomical visualization.Studies in health technology and informatics,vol.52,pp.1030-1032.

Bischoff,J.E.;Arruda,E.M.;Grosh,K.(2000):Finite element modeling of human skin using an isotropic,nonlinear elastic constitutive model.Journal of biomechanics,vol.33,pp.645-652.

Bradley,C.;Bowery,A.;Britten,R.;Budelmann,V.;Camara,O.;Christie,R.;Cookson,A.;Frangi,A.F.;Gamage,T.B.;Heidlauf,T.;Krittian,S.;Ladd,D.;Little,C.;Mithraratne,K.;Nash,M.;Nickerson,D.;Nielsen,P.;Nordbo,O.;Omholt,S.;Pashaei,A.;Paterson,D.;Rajagopal,V.;Reeve,A.;Rohrle,O.;Safaei,S.;Sebastian,R.;Steghofer,M.;Wu,T.;Yu,T.;Zhang,H.;Hunter,P.(2011):OpenCMISS:a multi-physics&multi-scale computational infrastructure for the VPH/Physiome project.Progress in biophysics and molecular biology,vol.107,pp.32-47.

Bradley,C.P.;Pullan,A.J.;Hunter,P.J.(1997):Geometric modeling of the human torso using cubic hermite elements.Annals of biomedical engineering,vol.25,pp.96-111.

Christie,G.R.;Nielsen,P.M.;Blackett,S.A.;Bradley,C.P.;Hunter,P.J.(2009):FieldML:concepts and implementation.Philosophical transactions.Series A,Mathematical,physical,and engineering sciences,vol.367,pp.1869-1884.

Flynn,C.;McCormack,B.A.(2010):Simulating the wrinkling and aging of skin with a multi-layer finite element model.Journal of biomechanics,vol.43,no.3 pp.442-448.

Garcia-Martinez,D.;Limbert,G.Year On the mechanics of the dermal-epidermal junction of human skin.In Computer methods in biomechanics and biomedical engineering.Salt Lake City,Utah,USA.

Hendriks,F.M.;Brokken,D.;van Eemeren,J.T.;Oomens,C.W.;Baaijens,F.P.;Horsten,J.B.(2003):A numerical-experimental method to characterize the non-linear mechanical behaviour of human skin.Skin Res Technol,vol.9,pp.274-283.

Huang,S.;DeGuzman,A.;Bucana,C.D.;Fidler,I.J.(2000):Nuclear factorkappaB activity correlates with growth,angiogenesis,and metastasis of human melanoma cells in nude mice.Clinical cancer research:an official journal of the American Association for Cancer Research,vol.6,pp.2573-2581.

Hunter,P.;Robbins,P.;Noble,D.(2002):The IUPS human Physiome Project.Pflugers Archiv:European journal of physiology,vol.445,pp.1-9.

Hunter,P.J.(1995):Myocardial constitutive laws for continuum mechanics models of the heart.Advances in experimental medicine and biology,vol.382,pp.303-318.

Hunter,P.J.;Borg,T.K.(2003):Integration from proteins to organs:the Physiome Project.Nature reviews Molecular cell biology,vol.4,no.3,pp.237-243.

Morey,P.(2003):Skin tears:a case review.Primary Intention:The Australian Journal of Wound Management,vol.11,pp.197.

Nam,J.;Aguda,B.D.;Rath,B.;Agarwal,S.(2009):Biomechanical thresholds regulate inflammation through the NF-kappaB pathway:experiments and modeling.PloS one,vol.4,e5262.

Saad,Y.;Schultz,M.H.(1986):Gmres-a Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear-Systems.Siam J Sci Stat Comp,vol.7,pp.856-869.

Sauermann,K.;Clemann,S.;Jaspers,S.;Gambichler,T.;Altmeyer,P.;Hoffmann,K.;Ennen,J.(2002):Age related changes of human skin investigated with histometric measurements by confocal laser scanning microscopy in vivo.Skin Res Technol,vol.8,pp.52-56.

Shim,V.B.;Hunter,P.J.;Pivonka,P.;Fernandez,J.W.(2011):A multiscale framework based on the physiome markup languages for exploring the initiation of osteoarthritis at the bone-cartilage interface.IEEE transactions on bio-medical engineering,vol.58,pp.3532-3536.

Shim,V.B.;Pitto,R.P.;Streicher,R.M.;Hunter,P.J.;Anderson,I.A.(2008):Development and validation of patient-specific finite element models of the hemipelvis generated from a sparse CT data set.J Biomech Eng.,vol.130,no.5 051010.

Tran,H.V.;Charleux,F.;Rachik,M.;Ehrlacher,A.;Ho Ba Tho,M.C.(2007):In vivo characterization of the mechanical properties of human skin derived from MRI and indentation techniques.Computer methods in biomechanics and biomedical engineering,vol.10,pp.401-407.

Werner,S.L.;Barken,D.;Hoffmann,A.(2005):Stimulus specificity of gene expression programs determined by temporal control of IKK activity.Science,vol.309,pp.1857-1861.