A Computational Modeling Framework for Heat Transfer Processes in Laser-Induced Dermal Tissue Removal

T.I.Zohdi

1 Introduction

One of the primary uses for lasers in the medical industry is for ablation of unwanted dermal tissue.There are many variants of the basic process for the removal of cancerous tissue,scars,stretch marks,wrinkles,liver spots(solar lentigenes),sun damage,thick scaly skin patches(actinic keratosis)and spider veins(telangiectasias).Some variants of the process,such as laser resurfacing,create controlled wounding,which spurs on the creation of new cells and guided healing.Further-more,laser scalpels,whereby a laser beam vaporizes soft tissue with high water content are widespread for the removal of benign and malignant tumors,bunions,ulcers,tissue fungus and tattoos(see Garfoualis(1989),Wynn and Michael(1986)and Gorman(1989)).

Figure 1:A schematic of a laser applied to a control volume of material.

For a laser to ablate tissue,the power intensity must be high enough to vaporize/burn the tissue.The characteristic power used in these applications is between 30 and 100 Watts.However,concerns that laser procedures,in general,can cause excessive microscale thermal injuries have been raised(for example,see Graber et al(2008)and Purschke et al,(2010)).The probability of healthy cells staying alive depends on the duration and temporal evolution of the temperature obtained.These concerns have motivated the present work.Our goal is to develop a computational tool by assembling relatively simple,physically meaningful,models.This can help guide the proper selection of the laser intensity,duration,etc.,in order to reduce the amount of damage to surrounding healthy tissue.

The outline of the paper is as follows:

•(I)We first analytically study the terms that contribute to achieving a target temperature,without phase transformations and mass ejection,by constructing an energy balance on a control volume accounting for:

•(a)incoming laser irradiance,

•(b)heat conduction to the body,

•(c)infrared radiation to the surroundings and

•(d)convection from a vacuum(needed in surgical procedures to collect unwanted debris).

•(II)We then develop a computational framework accounting for the above terms and further including:

•(a)phase transformations,including latent heats of transformation,and

•(b)mass transport(losses)due to ablation/burning/removal of tissue.

During the course of the analysis,non-dimensional parameter groups are identified in order to determine the relative contribution of each type of physics.Numerical examples are provided to illustrate the model’s behavior.The framework is,by design,straightforward to computationally implement,in order to be easily utilized by researchers in the field.

Remark:For the general characterization of the healing,growth and remodeling of the remaining(non-ablated)tissue,we refer the reader to Ambrosi et al(2011),Menzel and Kuhl(2012),Gktepe et al(2010),Kuhl et al(2007)and Zöllner et al(2012).

2 Contributing heat-transfer terms

In order to make estimates of the strength of a laser needed to induce a specified temperature rise,we first consider a lumped mass model for a sample of material shown in Figure 1(a control volume inside the dashed lines),without phase transformations and mass ejection.The governing equation is given by an overall energy balance(First Law of Thermodynamics):

whereMis the mass in the system,Cis the heat capacity and where we have the following contributing effects(denoted

•Absorbed incident optical radiation:whereIais the absorbed radiation per unit area,is the reflected radiation,Ris the reflectivity,Iiis the incident radiation per unit area,andAIis the area of the exposed(irradiated)surface.

•Conduction to the base(body):whereθis the temperature of the tissue to be removed,θBis the temperature of the body to which the tissue to be ablated is attached,ABis the area of the base surface(attached to the body),IKis the effective conductivity andhis the length scale over which the conduction occurs.

•Thermal re-radiation:whereθSis the temperature of the surroundings,0≤ε≤1 is the emissivity,σ=5.670373×10−8Watts/meter2−Kelvin4is the Stefan-Bolzmann constant,ARSis the area of the radiative surface exposed to the ambient surroundings andARB=ABis the area of the radiative surface to which the tissue to be ablated is attached.

•Convection(for example from a vacuum):whereHCis the effective surface convection coefficient andACis the area of the convective surface.Note that,oftentimes,a vacuum is needed in surgical procedures to collect unwanted debris.This leads to convective cooling.

3 Order of magnitude analysis

Normalizing the governing equation(Equation 1)yields

As mentioned at the outset,the power input for dermatological applications range fromP−=30≤P≤100=P+Watts,thus the irradiance(per unit area)is,assuming that it can be focussed entirely on the target

Clearly,for smallh,which is the case of interest,conduction can play significant role.For example,for an idealized cylindrical dermal protrusion,we have(Figure 2)

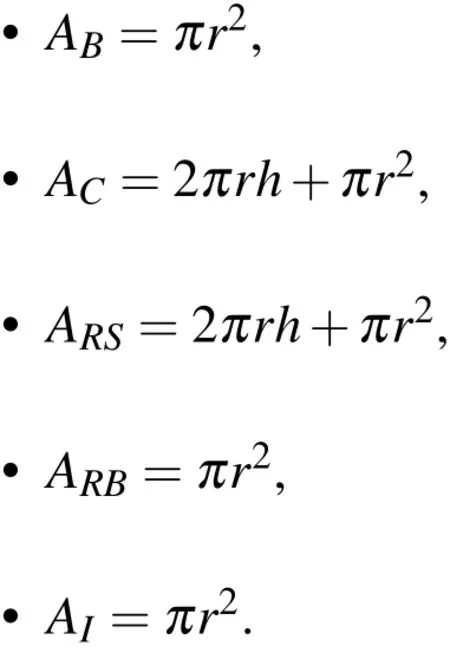
Forr≈h,this yieldsand forr>hyieldsThus,for a small target,for examplethe conductive term dominates the thermal radiation and convection and can be on the order of the laser input.

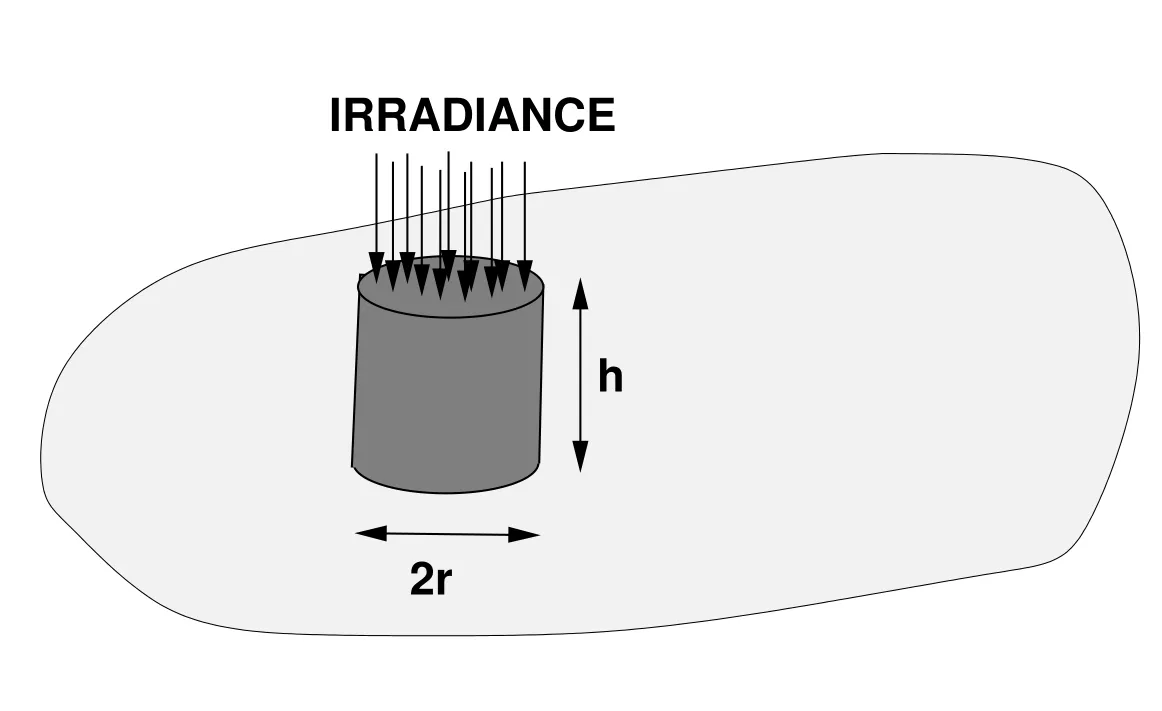
Figure 2:An idealized protrusion being irriadiated.

3.1 Special case:laser irradiance and conduction only

In order to extract qualitative trends,as a special case of the general class of problems,consider laser input and conduction,the simplified governing equation is

can be solved analytically,yielding(assumingθ(t=0)=θB)

We have the following observations:

3.2 Special case:laser irradiance,conduction and convection

In many cases,a vacuum is needed to collect the debris.This will lead to a large convection term.Therefore,as another special case of the general class of problems,let us add convection to the previous case,leading to

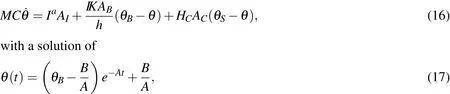
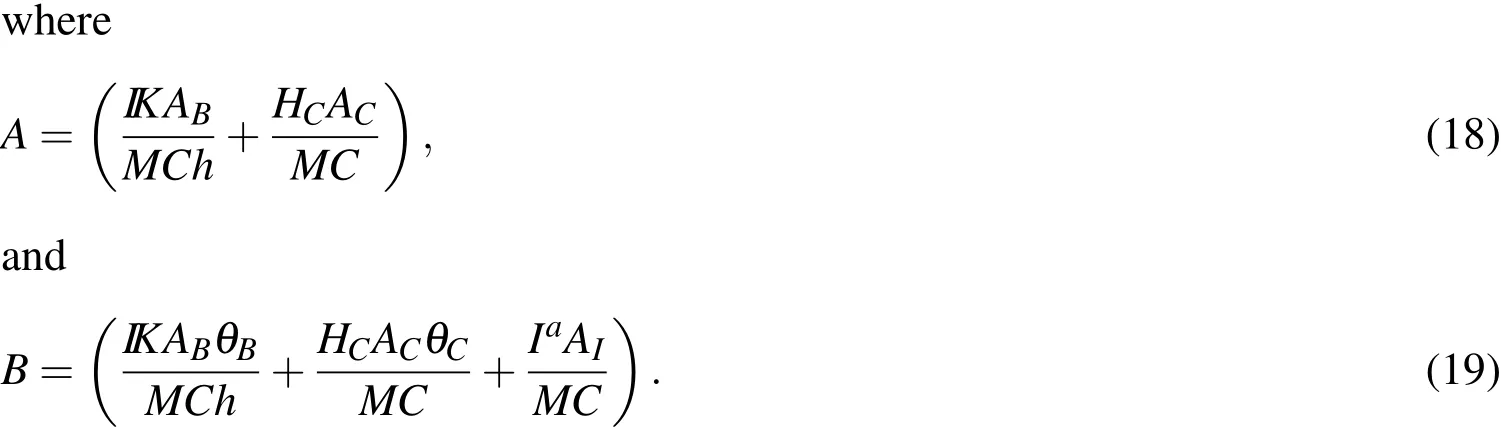
Inverting the solution to solve for the time for the temperature to meet a desired critical temperature,,yields

Clearly,when the argument of the Log-term is negative,this leads to an inability to ever reach the burning temperature.The denominator is always negative for the range of parameters of interest,thus negativity of the numerator dictates whether laser input is strong enough to meet the criteria.Explicitly,

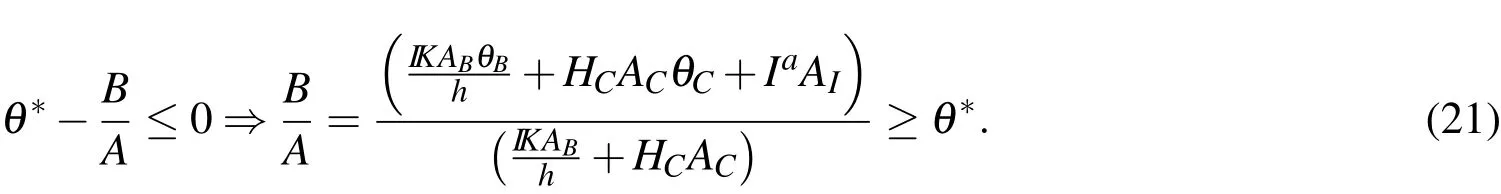
The inability to meet this criterion corresponds to either(or both)very strong conduction or convection for the laser intensity selected.Clearly,from Equation 20,asthe time to burning alsoFurthermore,from Equation 21,aswhich means that a desired specified critical temperature threshold,can never be met.

4 General time-transient simulations with phase-transformations and mass transfer

4.1 Phase transformations:solid⇒liquid⇒vapor

To include phase transformations,we consider the govering equation,with a thermally-dependent heat capacity(due to latent heats,and whether the material is solid,liquid or vapor),

and the following seven cases:

whereCSis the heat capacity of the solid,CLis the heat capacity of the liquid andCVis the heat capacity of the vapor and

Remark:Latent heats have a tendency to resist the phase transformations,achieved by adding the positive terms in the denominator,thus enforcing reduced temperature(during the phase transformation).1In the idealized limit,the temperature would be constant.This model is relatively straightforward to include within the upcoming computational framework.

4.2 Ablation and mass transfer

In order to simulate the time-transient response tissue to a general ablation process,we need to augment our governing equation(Equation 1)with a relation to track the mass transfer due to vaporization.Thereafter,we numerically discretize the coupled system.For example,a straightforward approach to describe the removal of tissue is via a thermally-activated evolution law for mass loss:

whereMis the total mass in the system,ζis the removal rate per unit mass,with the following conditions

4.3 System discretization

We employ a Forward Euler time discretization for Equation 1

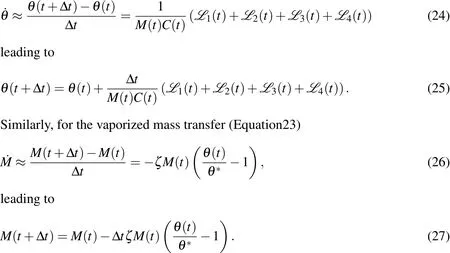
The solution procedure is straightforward.At a given time step:

•STEP 3:Check for phase-transformations and updateC(t+∆t),

•STEP 4:Increment time forward and

•STEP 5:Repeat STEPS 1-4 at the next time-step.

4.4 Examples

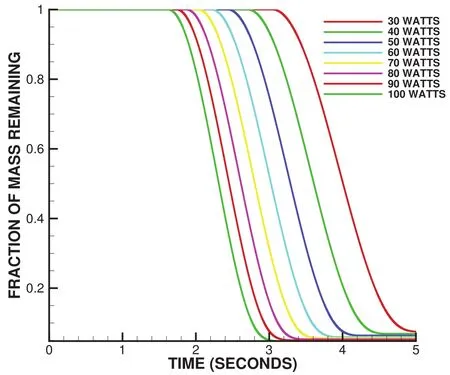
Figure 3:The percentage mass remaining in the control volume versus time as a function of different laser strengths,P=30→100Watts.The rightmost is the weakest(30 Watts)and the leftmost is the strongest(100 Watts).

We consider the idealized cylindrical protrusion shown in Figure 2.It is assumed that the rate of mass lost will be in the form of material ablated from the top.The parameters used were:

•h=0.005m,

•r=0.005m,

•θB=330Kelvin,

•θS=303Kelvin,

•θ∗=500Kelvin,

•30Watts≤P≤100Watts,

•ζ=10

•ρ=1000kg/m3,

•IK=1Watts/m−Kelvin,

•ε=0.1,

•HC=1Watts/m2−Kelvin.

For the phase transformations:

The general trends in Figure 3 indicate the percentage mass left versus time as a function of different laser strengths,P=30→100Watts.The rightmost is the weakest(30 Watts(red))and the leftmost is the strongest(100 Watts(green)).The time-stepping discretization parameter(∆t)was made sufficiently small so that the results were insensitive to further time-step size reductions.In other words,the depicted numerical results are essentially free of numerical error.During the simulations,the height(h)was reduced as the mass was ablated by computing(rdoes not change for this example)

Clearly,ash→0,conduction plays a much larger role.

Remark 1:To reliably extend this work,the spatial distribution of the thermal fields are of interest,and require the use of spatial discretization techniques based on,for example,Finite Difference or Finite Element Methods.Furthermore,an aspect of key interest is the characterization of potentially hazardous particulate ejecta.A complete model and numerical simulation of debris ejecta is currently underway by the author,and is based on methods found in Zohdi(2004,2007,2013)and Onate et al.(2008,2011)for the dynamics particulate flows, as well as more detailed optical modeling(see,for example,Zohdi(2006),Zohdi and Kuypers(2006)and Gross(2005)for overviews).The characteristics of the burned tissue are important in this regard.We refer the reader to studies of damaged tissue in Cushing(2007),Lederer and Kroesen(2005),Fontanarosa(1993),Adukauskiene,Vizgirdaite and Mazeikiene(2007),Cooper(1995)and Xu,Zhu and Wu(1999),related to third degree burns,which extend through the entire dermis,resulting in a loss of elasticity(stiffening)and tissue dryness,and fourth degree burns,which extend through the subcutaneous skin tissue to the muscle and bone leading to a charred,dry,stiff material.2Thermal interaction can be classified as(a)coagulation,(b)vaporization,(c)carbonization and(d)melting.These processes likely involve the mechanics of detachment(Yoon and Mofrad,2011)and strongly coupled thermal,diffusive and chemical effects in solids.For an in depth mathematical analysis of such coupled systems,in particular instabilities,we refer the reader to Markenscoff(2001a,2001b,2003).

Remark 2:With regards to the mechanisms that produce ejecta,there are many possibilities.For example,in thermal or photothermal ablation,laser light energy is converted to lattice vibration before breaking of bonds,which liberates atomicscale material,while in photochemical/electronic ablation direct electronically induced vibration occurs,whereas hydrodynamical ablation refers to micrometer droplets following from the molten phase,whereas exfoliation is an erosive mechanism by which material is removed as flakes.Note that all of the mechanisms can occur simultaneously.

Remark 3:Laser-based procedures can involve the use of special types of dyes to increase absorption of the tissue,referred to as sclerostomics.The dyes are applied by electrophoresis,i.e.electrical current is used to direct dye into tissue.This can be used for targeted interaction.The process allows a surgeon to tailor the process for each patient,as well as for different parts of the body,in a more precise manner than with chemical peels alone(Sadick et al(2004)and Lim et al(2007)).

5 Summary

This work developed a straightforward model and a corresponding solution algorithm for the rapid simulation of the laser-induced removal of dermatological tissue,by developing simple models for the heat transfer mechanisms that occur in the overall process,including:(a)incoming laser irradiance,(b)heat conduction to the body,(c)infrared radiation to the surroundings,(d)convection from a vacuum needed in surgical procedures to collect unwanted debris,(e)phase transformations,including latent heats of transformation,and(f)mass transport(losses)due to burning and ablation of the target tissue. Non-dimensional groups were identified to indicate relative contribution of each type of physics.Numerical examples were provided to illustrate the model’s behavior which,by design,is straightforward to computationally implement by researchers in the field.In closing,we mention that modeling process can be extended beyond dermal applications,for example to surface ablation of the cornea for several types of eye refractive surgery,using an excimer laser system(LASIK and LASEK),which is used to correct near and farsightedness in vision,and photorefractive keratectomy(PRK)procedures,which use an excimer laser to reshape the cornea by removing tiny portions of tissue(see Cuschieri et al(1999),Schweinger and Hunter(1992)and Morris and Wood(2000)).Also,extensions to laser endometrial ablation,which removes part of the uterine wall in women with menstruation complications,are possible.In general,laser ablation can also be used on benign and malignant lesions in various organs,such as the reduction of benign thyroid nodules(Valcavi et al(2010),and elimination of malignant liver lesions(Pacella et al(2009)and Garfoualis(1989)).This is broadly referred to as laser-induced interstitial thermotherapy.Modeling of these processes is currently under investigation by the author.

Adukauskiene,D.;Vizgirdaite,V.;Mazeikiene,S.(2007):Electrical injuries.Medicina(Kaunas),vol.43,no.3,pp.259-66.

Ambrosi,D.;Ateshian,G.A.;Arruda,E.M.;Cowin,S.C.;Dumais,J.;Goriely,A.;Holzapfel,G.A.;Humphrey,J.D.;Kemkemer,R.;Kuhl,E.;Olberding,J.E.;Taber,L.A.;Garikipati,K.(2011):Perspectives on biological growth and remodeling.J Mech Phys Solids,vol.59,pp.863-883.

Cooper,M.A.(1995):Emergent care of lightning and electrical injuries.SeminNeurol.vol.15,no.3,pp.268-78.

Cuschieri,A.;Steele,R.J.;Moossa,A.R.(1999):Essential Surgical Practice.4th ed.London:Hodder Arnold Publication.

Cushing,T.(2011):Electrical Injuries in Emergency Medicine.Medscape Reference.Web.29,September 2011.

Fontanarosa,P.B.(1993):Electrical shock and lightning strike.Ann Emerg Med.,vol.22,Issue 2,Part 2,pp.378-87.

Garfoualis,M.G.(1989):Soft Tissue Lesions.In Ballow D.P.M.,Edward B.Laser Surgery of the Foot(First Edition ed.).International Society of Podiatric Laser Surgery.pp.65-72.

Göktepe,S.;Abilez,O.J.;Parker,K.K.;Kuhl,E.(2010):A multiscale model for eccentric and concentric cardiac growth through sarcomerogenesis.J Theor Bio,vol.265,pp.433-442.

Gorman,J.B.(1989):Clinical Application of the Carbon Dioxide Laser to Podiatric Nail Pathologies:A Definitive Review of the Literature".In Ballow D.P.M.,Edward B.Laser Surgery of the Foot(First Edition ed.).International Society of Podiatric Laser Surgery.pp.109-110.

Graber,E.M.;Tanzi,E.L.;Alster,T.S.(2008):Side effects and complications of fractional laser photothermolysis:experience with 961 treatments.Dermatol Surg.,vol.34,no.3,pp.301-307.

Gross,H.(2005):Handbook of optical systems.Fundamental of technical optics.H.Gross,Editor.Wiley-VCH.

Kuhl,E.;Maas,R.;Himpel,G.;Menzel,A.(2007):Computational modeling of arterial wall growth:Attempts towards patient specific simulations based on computer tomography.Biomech Mod Mechanobio,vol.6,pp.321-331.

Lederer,W.;Kroesen,G.(2005):Emergency treatment of injuries following lightning and electrical accidents.Anaesthesist,vol.54,no.11,pp.1120-1129.

Lim,H.W.;Hawk,J.L.M.(2007):Evaluation of the photosensitive patient.In:Photodermatology,Lim,H.W.,Honigsmann,H.,Hawk,J.L.M.(Eds),Informa Healthcare,New York,pp.139.

Markenscoff,X.(2001a):Diffusion induced instability.Quarterly of Applied Mechanics,vol.LIX,no.1,pp.147-151.

Markenscoff,X.(2001b):Instabilities of a thermo-mechano-chemical system.Quarterly of Applied Mechanics,vol.LIX,no.3,pp.471-477.

Markenscoff,X.(2003):On conditions of“negative creep”in amorphous solids.Mechanics of Materials,vol.35,Issues 3-6,pp.553-557.

Morris,P.J.;Wood,W.C.(2000):Oxford Textbook of Surgery,Volume 2.

Menzel,A.;Kuhl,E.(2012):Frontiers in growth and remodeling.Mech Res Comm,vol.42,pp.1-14.

Onate,E.;Idelsohn,S.R.;Celigueta,M.A.;Rossi,R.(2008):Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows.Computer Methods in Applied Mechanics and Engineering,vol.197,no.19-20,pp.1777-1800.

Onate,E.;Celigueta,M.A.;Idelsohn,S.R.;Salazar,F.;Suárez,B.(2011):Possibilities of the Particle Finite Element Method for fluid-soil-structure interaction problems.Computational Mechanics,vol.48,pp.307-318.

Pacella,C.M.;Francica,G.;Di Lascio,F.M.;Arienti,V.;Antico,E.;Caspani,B.;Magnolfi,F.;Megna,A.S.;Pretolani,S.;Regine,R.;Sponza,M.;Stasi,R.(2009):Long-term outcome for cirrhotic patients with early hepatocellular carcinoma treated with ultrasound-guided percutaneous laser ablation:a retrospective analysis.J Clin Oncol,vol.16,pp.2615-21.

Pompili,M.;Pacella,C.M.;Francica,G.;Angelico,M.;Tisone,G.;Craboledda,P.;Nicolardi,E.;Rapaccini,G.L.;Gasbarrini,G.(2010):Percutaneous laser ablation of hepatocellular carcinoma in patients with liver cirrhosis awaiting liver transplantation.European Journal of Radiology,vol.74,issue.3,pp.e6-e11.

Purschke,M.;Laubach,H.J.;Anderson,R.R.;Manstein,D.(2010):Thermal injury causes DNA damage and lethality in unheated surrounding cells:active thermal bystander effect.The Journal of investigative dermatology,vol.130,no.1,pp.86-92.

Sadick,N.S.;Weiss,R.;Kilmer,S.;Bitter,P.(2004):Photorejuvenation with intense pulsed light:results of a multi-center study.Journal of Drugs in Dermatology,vol.3,no.1,pp.41-49.

Schwesinger,W.H.;Hunter,J.G.(1992):Laser in General Surgery.Surgical Clinics of North America.

Valcavi,R.;Riganti,F.;Bertani,A.;Formisano,D.;Pacella,C.M.(2010):Percutaneous Laser Ablation of Cold Benign Thyroid Nodules:A 3-Year Follow-Up Study in 122 Patients.Thyroid.vol.20,no.11,pp.1253-1261.

Wynn,D.P.M.;Michael,H.(1986):Soft-Tissue Bunion Repair with a CO2 Surgical Laser.The Journal of Current Podiatric Medicine,vol.35,no.10,pp.27-28.

Xu,X.;Zhu,W.;Wu,Y.(1999):Experience of the treatment of severe electric burns on special parts of the body.Annals of the New York Academy of Sciences.

Yoon,S.H.;Chang,J.;Lin,L.;Mofrad,M.R.K.(2011):A biological bread-board platform for cell adhesion and detachment studies.Lab on a Chip,vol.11,no.20,pp.3555-62.

Zohdi,T.I.(2006):Computation of the coupled thermo-optical scattering properties of random particulate systems.Computer Methods in Applied Mechanics and Engineering,vol.195,pp.5813-5830.

Zohdi,T.I.;Kuypers,F.A.(2006):Modeling and rapid simulation of multiple red blood cell light scattering.Proceedings of the Royal Society Interface,vol.3,no.11,pp.823-831.

Zohdi,T.I.(2004):A computational framework for agglomeration in thermochemically reacting granular flows.Proceedings of the Royal Society,vol.460,no.2052,pp.3421-3445.

Zohdi,T.I.(2007):Computation of strongly coupled multifield interaction in particle- fluid systems.Computer Methods in Applied Mechanics and Engineering,vol.196,pp.3927-3950.

Zohdi,T.I.(2013):Numerical simulation of charged particulate cluster-droplet impact on electrified surfaces.Journal of Computational Physics,vol.233,pp.509-526.

Zöllner,A.M.;Buganza Tepole,A.;Kuhl,E.(2012):On the biomechanics and mechanobiology of growing skin.J Theor Bio,vol.297,pp.166-175.