模拟退火的粒子群BP神经网络数据处理探讨

田建波, 程 喆,陈 于

（1.中国人民解放军61365部队,天津 300140；2.中国地质大学（武汉）信息工程学院，湖北 武汉430074；3.中国人民解放军61175部队，湖北 武汉430074）

模拟退火的粒子群BP神经网络数据处理探讨

田建波1, 程 喆2,3,陈 于2

（1.中国人民解放军61365部队,天津 300140；2.中国地质大学（武汉）信息工程学院，湖北 武汉430074；3.中国人民解放军61175部队，湖北 武汉430074）

为了提高监测数据分析与预报的准确性、实时性，提出将模拟退火算法与粒子群BP神经网络相结合应用于变形监测数据处理中。分别分析了3种方法的原理和计算过程，阐述了新方法的计算步骤，并通过实例说明该方法比传统的BP神经网络法拟合和预报效果更好。

模拟退火法；粒子群算法；BP神经网络；监测数据

BP神经网络是一种采用误差反向传播训练算法的多层前馈神经网络，在处理非线性、无规则的问题时具有很强的优越性，广泛应用于大坝变形预测与安全监控[1,2]、工程变形监测[3]、滑坡位移预测[4,5]和GPS水准高程转换[6]等领域；但其存在收敛速度慢、输出结果容易受初始值影响等缺点。针对这些缺点，提出了遗传模拟退火算法的BP算法[7]、BP网络优化的并行模拟退火遗传算法[8]、基于遗传算法的模糊神经网络结构和参数优化[9]、基于L-M算法的BP神经网络分类器[10]、改进激活函数的人工神经网络[11]等改进方法。粒子群优化算法是一种基于群体智能方法的计算技术，收敛速度快，但精度一般较低；而基于粒子群优化算法的多因子自适应滤波[12]和改进粒子群耦合[13]方法能较好地克服此缺点。模拟退火法是基于模拟固体物质退火过程的优化算法[14,15]，输出结果质量高但过程时间长。鉴于3种方法的优缺点，本文提出将粒子群优化算法与模拟退火法相结合应用于BP神经网络中，进行GPS监测数据处理分析，通过与传统的BP神经网络对比研究，证明该方法的可行性与实用性。

1 模拟退火的粒子群BP神经网络预测模型

模拟退火的粒子群BP神经网络模型在进行变形监测分析时，是以模拟退火法BP神经网络为基础，运用粒子群优化算法进行初始权值的计算。

1.1 BP神经网络

BP神经网络是基于误差逆向传播训练算法的多层前馈神经网络，由输入层、隐含层和输出层组成。信号正向传播的输出值与预定值相比得出误差，误差反向传播训练纠正神经元的权值和阈值，如此迭代，使误差逐步减小，直至误差小于给定值时，学习结束，如图1所示。其中，W为各个输入神经元与隐含层神经元以及隐含层神经元与输出层神经元的连接权；V为各个隐含层以及输出层神经元的阈值。

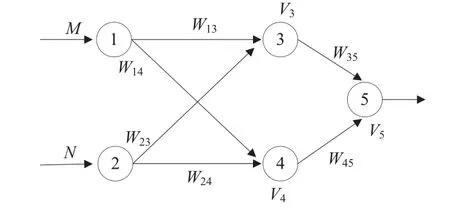
图1 BP神经网络图

1.2 粒子群优化算法

粒子群优化算法(PSO)是一种基于群体智能方法的演化计算技术，每个优化问题的可能解都是搜索空间的一个粒子，每个粒子有优化函数决定的适应值，还有决定粒子方向和距离的速度。PSO初始化为一群随机粒子进行迭代寻优。每次寻优的单个粒子都通过跟踪当前种群中的最优解和当前“邻居”中的最优解来更新自己，最终找到最优解。

粒子群优化算法的具体流程为[1]：

1）初始化：在允许的范围内随机产生初始粒子的位置x0和速度v0，每个粒子的局部最优解pbest坐标设置为其当前位置，计算出所有个体极值点的适应度值，选取所有个体极值点适应度值中最好的作为全局最优解gbest，gbest坐标设置为最好粒子的当前位置。

2）粒子评价：重新计算粒子的适应度值，如果优于当前粒子个体极值点适应度值，则将pbest设置为该粒子的位置，并更新个体极值点适应度值。如果所有粒子的个体极值点适应度值中最好的优于全局极值，则更新全局极值并将gbest设置为该粒子的位置。

3）更新粒子：

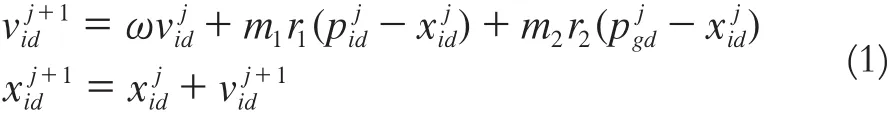
式中，i=1,2,3，…，m，为粒子的总个数；d=1,2,3，…，D，为搜索空间的维数；ω为惯性权重；m1、m2为权重因子；r1、r2为0到1之间的随机数为第 j次迭代的粒子i位置矢量的第d维分量为第j次迭代的粒子i飞行速度矢量的第d维分量为第j次迭代的粒子i最好个体位置pbest的第d维分量为第j次迭代的粒子群最好位置gbest的第d维分量。

4）检验结果：若达到迭代结束的条件(迭代次数达到或迭代误差小于给定值)则结束迭代，输出最优解，否则转到步骤2）。

1.3 模拟退火法

模拟退火法（SA）是基于组合优化问题与固体物质退火过程的相似性,在模拟固体物质退火的过程中寻求最优解[2]。算法具体步骤如下：

1）指定退火法初始温度T0和当前状态i。

2）通过扰动产生新状态j，计算目标函数Fi和Fj，如果Fi＞Fj，接受j为当前温度的新状态；否则通过概率判断是否接受新的状态：

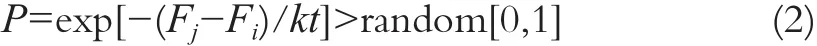
式中，k为boltzmann常数。

1.4 模拟退火的粒子群BP神经网络预测模型

针对BP神经网络的初始连接权初始化效果不一定理想和收敛较慢的实际情况，使用粒子群优化算法优化初始权，模拟退火法代替误差反向传播训练法，提高神经网络收敛速度和学习能力。具体流程如下：

1）BP神经网络的构建。将影响变形监测的因素（气温、季节、空气湿度等）作为输入层神经元，将变形量（水平、垂直位移等）作为输出层神经元。隐含层神经元的个数一般由式（3）确定：

式中，l为隐含层神经元个数；p为输入层神经元个数；q为输出层神经元个数。

2）给定粒子总数m、惯性权重ω、权重因子m1和m2、搜索空间维数D（网络中所有连接权的个数）、

3）选定输出层误差平方和为适应度函数，即

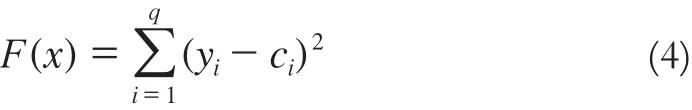
式中，q为输出层神经元个数(一般为变形量)；y和c分别为实测值和输出值。

4）随机初始化连接权为一群粒子，具体编码格式如下：

粒子位置：X1，X2，X3，…，XD

粒子速度：V1，V2，V3，…，VD

适应度函数：F（x）

5）计算各个粒子的适应度。

6）将每个粒子的适应度和局部最好适应度pbest比较，若超过局部最好适应度pbest，则将该粒子的位置作为局部最好pbest；再将该粒子的适应度与全部最好适应度gbest比较，若超过全局最好适应度gbest，将该粒子作为全局最好gbest。

7）利用式（1）更新粒子的具体位置X和速度V。

8）在解空间进行搜索，如果超过规定的迭代次数或达到预定的精度要求，停止迭代，将最优解gbest作为BP神经网络的初始权值；否则转入步骤5）。

9）将输入和输出的数据统一进行格式化处理：

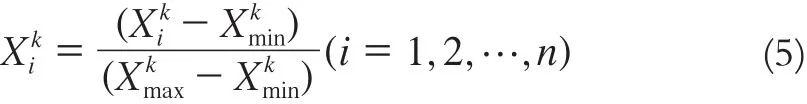
10）利用Rand函数进行输出层和隐含层的阈值V的初始化，所有连接权值已经初始化完毕。初始温度T0可以随意给定。

11）BP神经网络根据已有的输入样本、连接权和阈值得出输出结果，与理想结果相比得出误差；再进行一次误差反向传播训练法得出新的连接权和阈值。

12）将新的阈值V和连接权W作为模拟退火法在该温度T0下的初态j[3,4]，新状态按照柯西分布：

式中，x为0到1之间的随机数；t为当前温度。

13）确定能量函数(目标函数)：

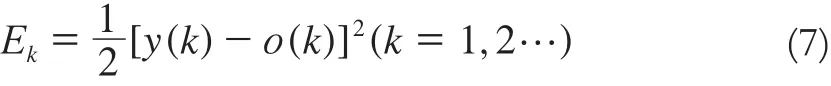
式中，y（k）为实际值；o（k）为网络完成输出后，执行Metropolis准则并满足内循环的停止准则，输出的权值和阈值[5-7]。

14）将输出权值和阈值作为网络的新值计算目标函数，如果目标函数与实际值的差满足精度要求，停止外循环并输出变形观测数据的预测值；否则降温处理转到步骤12）。

具体流程如图2所示。

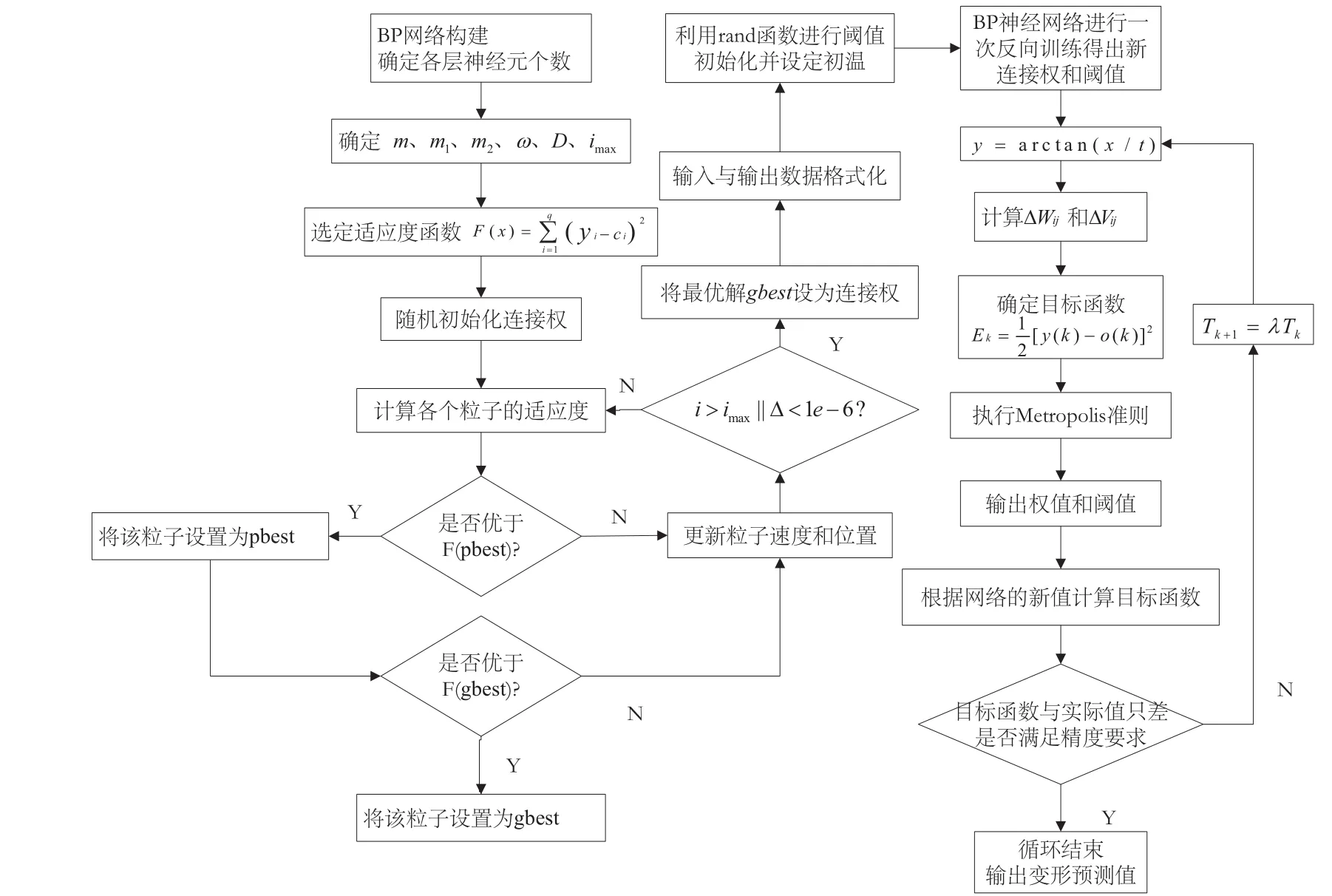
图2 算法流程图

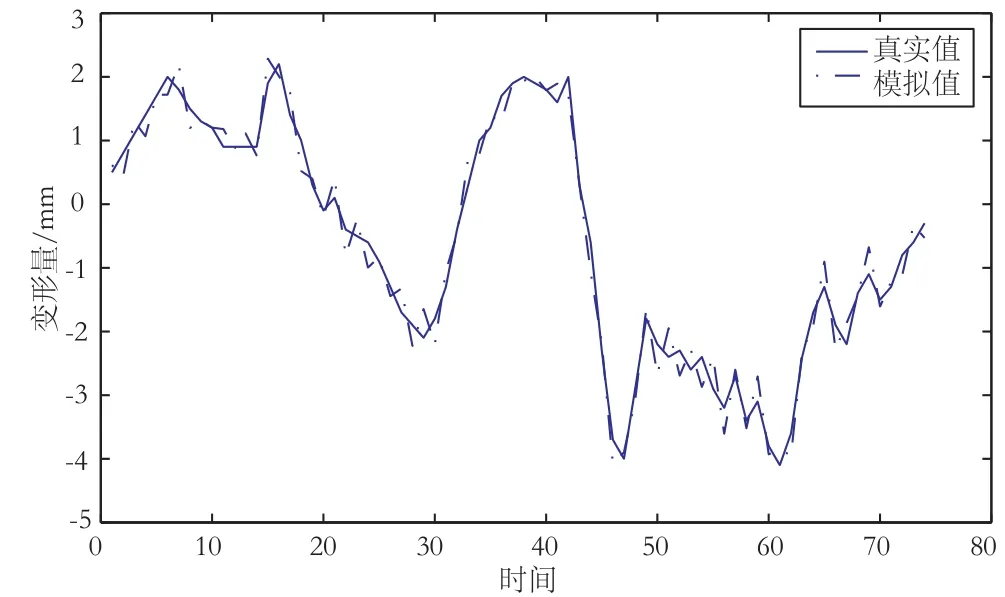
图3 BP神经网络模拟效果图

2 算例与分析

选取某大坝2009-05-17～2009-10-19监测数据，分析沿河流方向的位移变形量。将2009-05-17作为基准日，对监测数据坐标、水位和气温进行处理，得到相对于基准日的相对坐标、水位和气温；确定BP神经网络输入层有水位分量、温度因子、时效因子3类节点，输出层节点一个，即X方向位移量；分别采用单纯的BP神经网络法和模拟退火的粒子群BP神经网络进行模拟，效果如图3、图4所示。

新方法的模拟效果要明显优于单纯的BP神经网络方法；再分别利用2种方法对2009-10-12～2009-10-19的变形量进行预报（见表1）。

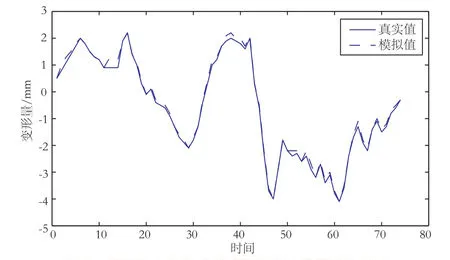
图4 模拟退火的粒子群BP神经网络模拟效果图

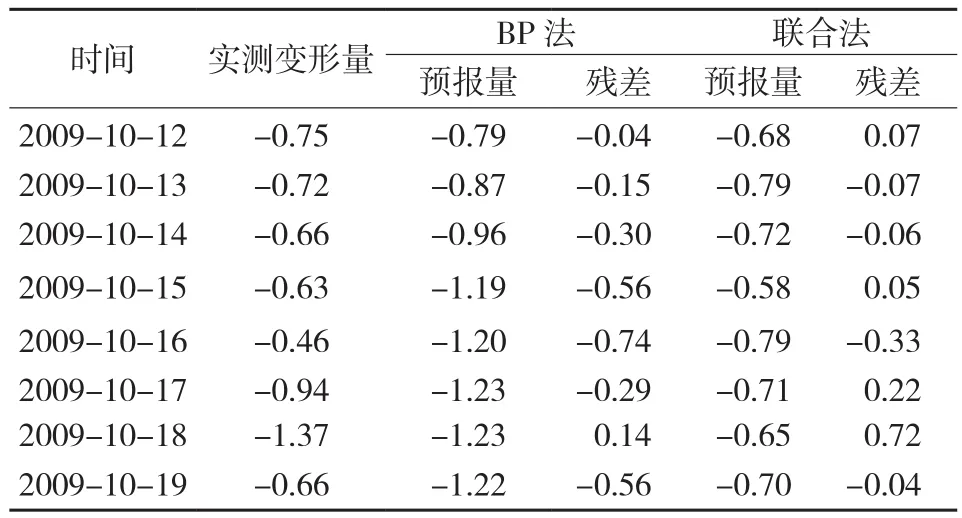
表1 模拟退火的粒子群BP神经网络与单纯BP神经网络预报值对比分析表/mm

由表1可知，模拟退火的粒子群BP神经网络预报值残差要明显小于单纯BP神经网络残差，预报值更准确。

3 结 语

本文提出模拟退火的粒子群BP神经网络，将模拟退火法、粒子群法和BP神经网络结合起来，经过实例验算证明其预测效果优于单纯的BP神经网络法。该方法对于提高GPS监测数据处理分析的速度与灵敏度具有实际意义。

[1] 李捷斌, 孔令杰． 基于Kalman滤波的BP神经网络方法在大坝变形预测中的应用[J]． 大地测量与地球动力学, 2009, 29(4): 124-128

[2] 苏怀智, 吴中如, 温志萍，等． 基于模糊联想记忆神经网络的大坝安全监控系统建模研究[J]． 武汉大学学报：工学版, 2001, 34(4): 21-25

[3] 刘祖强, 张正禄． 工程变形监测分析预报的理论与实践[M]．北京：中国水利水电出版社，2008

[4] 彭令, 牛瑞卿, 赵艳南，等． 基于核主成分分析和粒子群优化支持向量机的滑坡位移预测[J]． 武汉大学学报：信息科学版, 2013, 38(2): 148-154

[5] 武雪玲, 任福, 牛瑞卿． 多源数据支持下的三峡库区滑坡灾害空间智能预测[J]． 武汉大学学报：信息科学版, 2013, 38(8): 963-969

[6] 王殊伟, 李斐, 柯宝贵，等． 基于BP神经网络算法的GPS水准高程转换[J]． 武汉大学学报：信息科学版, 2009, 34(10): 1 190-1 195

[7] 张世龙, 唐雅娜． 基于遗传模拟退火算法的BP算法研究[J]．现代计算机, 2007(2): 30-33

[8] 刘月娥, 何东健, 李峥嵘． 一种用于BP网络优化的并行模拟退火遗传算法[J]．计算机应用, 2006, 26(1): 204-207

[9] 周志坚, 毛宗源． 一种基于遗传算法的模糊神经网络结构和参数优化[J]． 华南理工大学学报：自然科学版, 1999, 27(1): 26-33

[10] 王建梅, 覃文忠． 基于L-M算法的BP神经网络分类器[J]．武汉大学学报：信息科学版, 2005, 30(10): 928-932

[11] 胡耀垓, 李伟, 胡继明． 一种改进激活函数的人工神经网络及其应用[J]． 武汉大学学报：信息科学版, 2004, 29(10): 916-920

[12] 聂建亮, 程传录, 郭春喜，等． 基于粒子群优化算法的多因子自适应滤波[J]． 武汉大学学报：信息科学版, 2013, 38(2): 136-140

[13] 王伟, 沈振中． 大坝统计预警模型的改进粒子群耦合方法[J]．武汉大学学报：信息科学版, 2009, 34(8): 987-992

[14] 范千, 许承权．单纯形—模拟退火混合算法及其在参数估计中的应用[J]． 地理空间信息, 2005， 3(3): 57-59

[15] 胡山鹰, 陈丙珍, 何小荣，等．非线性问题全局优化的模拟退火法[J]． 清华大学学报：自然科学版, 1997, 37(6): 5-9

P258

B

1672-4623（2014）03-0069-04

10.11709/j.issn.1672-4623.2014.03.022

田建波，硕士，高级工程师，研究方向为GNSS数据处理与应用。

2014-01-20。

项目来源：湖北省自然科学基金资助项目（2011CDB350）。