含圆孔双压电陶瓷的动态性能研究

李 冬， 王慧聪， 宋天舒

(1. 河北交通职业技术学院土木工程系，河北 石家庄 050091; 2. 哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001)

含圆孔双压电陶瓷的动态性能研究

李 冬1， 王慧聪1， 宋天舒2

(1. 河北交通职业技术学院土木工程系，河北 石家庄 050091; 2. 哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001)

采用Green函数法研究界面附近含圆形孔洞的两半无限压电陶瓷对SH波的散射问题。首先利用复变函数和多极坐标的方法构造出适合于本文问题的位移Green函数和电场Green函数。然后利用契合思想，根据界面上的连续性条件建立起求解问题的第一类Fredholm型积分方程。得到了孔边周向剪应力动应力集中系数的解析表达式。最后作为算例，给出了界面两侧圆孔的两组动应力集中系数的计算结果图并进行了讨论。

动应力集中系数； 双压电陶瓷； 界面附近圆孔； Green函数

0 引 言

目前，广泛应用于工程实际的压电材料主要是压电陶瓷。压电陶瓷是典型的脆性材料，具有断裂韧性低和缺陷敏感性高的特点。因此，用压电陶瓷制作的器件或结构在使用过程中，常会因制造和使用过程中出现的孔洞、裂纹等缺陷引起的应力集中而导致其设计功能的丧失，这限制了压电陶瓷更广泛的应用和相关器件性能的进一步提高。因而，弄清楚压电陶瓷断裂的物理力学机制，成为近年来固体力学和材料物理领域内的重要研究课题[1]。近年来，Gao等[2]利用复变方法研究了含有椭圆形孔洞的二维压电材料在无穷远处受荷载作用时的问题，给出了孔外及孔内场的封闭解答。Lee等[3]研究了一个含有斜椭圆形孔洞的压电板在无穷远处作用混合形式的电机械载荷时的断裂问题。利用Paschen原理Gao[4]分析了一个充满空气的椭圆形孔洞的压电体受电机械载荷联合作用时孔洞内的局部放电问题。Sosa等[5]在二维电弹性理论框架下对含椭圆形孔洞的压电材料问题进行了研究。采用Stroh公式Chung等[6]对二维各向异性压电材料中含椭圆形孔洞和椭圆形刚性夹杂问题分别进行了研究。周志东等[7]以孔边加载下的Stroh广义应力及位移表达式为基础，在精确电学边界条件下得到了介质中任意点处作用一广义点荷载时应力的函数表达式。戴隆超等[8]利用复变函数方法对含椭圆形孔洞的横观各向同性压电材料在远场均匀载荷作用下的力学问题进行了分析。

以上这些工作，大都是静态方面的研究，关于动态方面的研究相对较少。本文即对含圆孔缺陷双相压电陶瓷的动态问题进行分析，讨论了在一组稳态力电波场作用下，压电陶瓷的物理参数和几何参数及入射波场的频率对圆孔周边动应力集中系数的影响。

1 问题的表述

双压电陶瓷界面两侧含圆形孔洞的模型如图1所示。两圆形孔洞的半径分别为R1和R2，圆心与界面的距离分别为h1和h2，两圆心之间沿界面方向相距d，一组稳态的力电场沿与界面成α0的方向入射。引入复变量设电极化方向垂直于xy平面，则稳态的反平面动力学问题的控制方程可写为[9]：

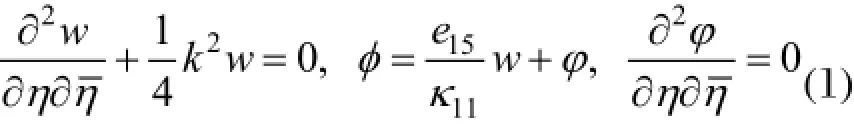
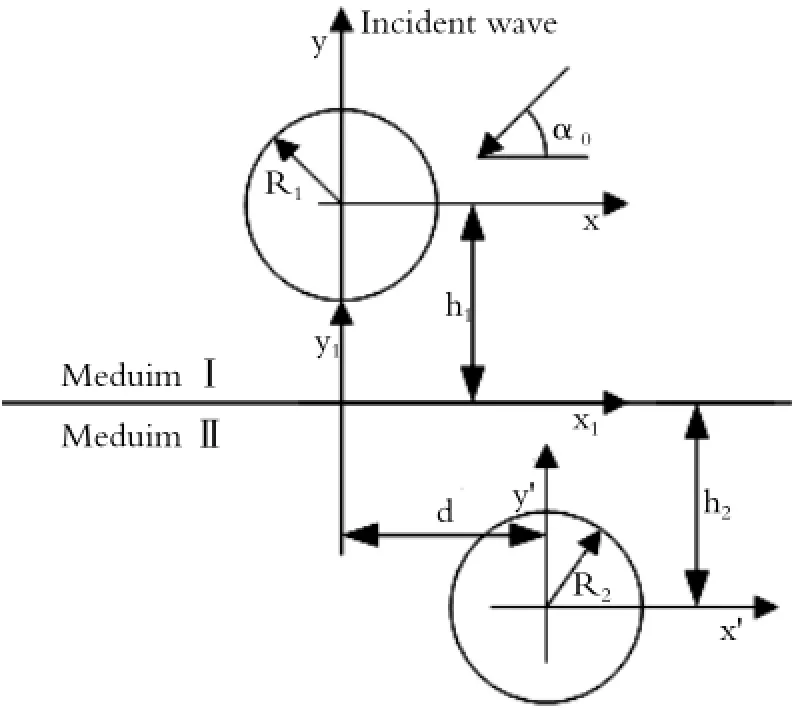
图1 界面附近含圆孔双相压电陶瓷的力学模型Fig.1 The mechanical model of piezoelectric bimaterials with a circular cavity near the interface

圆孔处的边界条件可表示为：

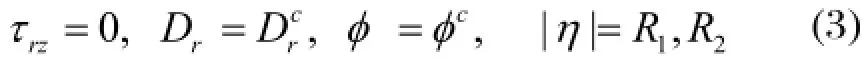
上标c分别表示圆孔内的物理量，下同。

2 Green函数的推导

研究的Green函数是一个具有圆形孔洞的压电陶瓷弹性半空间在其水平表面上任意一点承受时间谐和的出平面线源荷载作用时位移函数和电场函数的基本解，满足控制方程(1)，它由线源荷载产生的扰动和圆孔激发的散射波两部分组成，分别用上标i和s表示，扰动部分可表示为[10]：

散射波部分可写为：

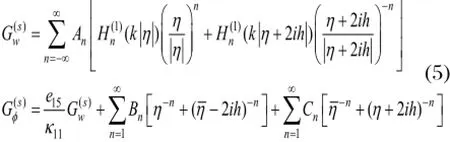
则本问题的位移Green函数wG和电场Green函数Gφ的表达式可分别表示为：

圆孔内只有电场而无弹性场，其电位势c

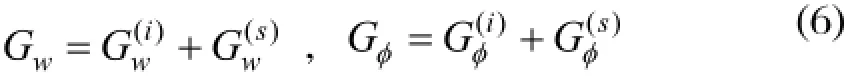
Gφ应达式可写为：

依波以设计为龙头，以技术为保障，2018年，依波在工业设计中心和企业技术中心的“双中心”建设方面，取得了一系列重要成果：依波工业设计中心，坚持在腕表设计领域不断创新与突破，推出的一系列新款腕表都得到了国内外专业机构的认可与广大市场的好评，多项作品屡次斩获 “蓝光杯”、“德国红点奖”、“深圳礼物”、“TIA首席设计官”等设计大奖。此外，依波与深圳市设计联合会联合成功举办首届“时计之星——依波腕表创意设计大赛”，为好设计发声。而依波中心实验室荣获国家CNAS认证，钟表检测和校准服务的技术能力与国际接轨，中心实验室也在新材料、新工艺的研发等方面取得多项成果。

利用条件(3)可求得未知系数An, Bn, Cn, Dn, En的值。

3 双相压电陶瓷界面附近圆孔对波的散射

当关于时间谐和的波以与界面成α0角度入射时，陶瓷中的入射、反射和透射力电场的表达式分别可以写为[11]：其中，w1, φ1, w2, φ2与的关系由界面上的连续性条件可得。

陶瓷I、II中分别由圆形孔洞产生的散射力电场为w(Is)、φ(Is)和w(IIs)、，当其同时满足界面上应力自由的条件时，它们的表达式可分别写为：

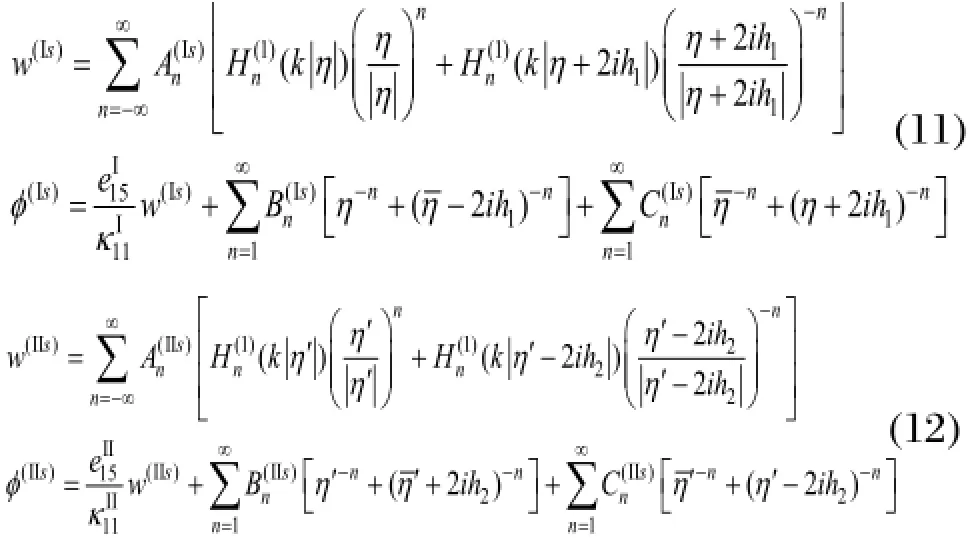
两圆孔内电场的表达式分别为：

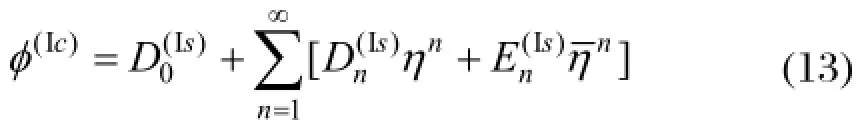
其中，未知系数的求法与Green函数中一样。

根据得到的Green函数和陶瓷I、II中的力电场，利用契合思想[10]构造出双相压电陶瓷界面附近圆形孔洞对入射波场的散射解，如图2所示，从而将问题转化为求解一组定解积分方程。

图2 形成界面附近含圆孔的双相压电陶瓷Fig.2 Forming piezoelectric bimaterials with a circular cavity near the interface

其构造过程是：首先沿y=-h1界面将双相压电陶瓷剖分为上半空间介质Ⅰ和下半空间介质Ⅱ。在半空间介质Ⅰ的剖面上总位移wI、总电位势φI、总应力和总电位移分别为：

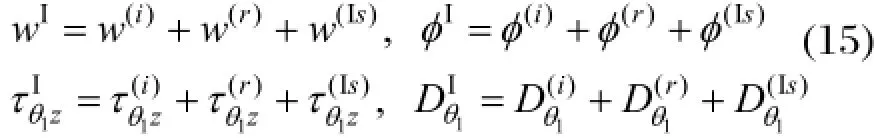
然后，将剖分后的两个半空间“装配”起来，同时为了满足剖分面上的应力、电位移、电位势和位移的连续性条件，需在介质Ⅰ、Ⅱ中剖分界面的相应区域施加一对待求的反平面外力系f1( r01,θ01)、f2(r01, θ01)和一对待求的平面内外电场 f3(r01,θ01)、 f4( r01,θ01)。利用契合面上的四个连续性条件便可得求解未知外力系和外电场的定解积分方程组。

契合界面上的应力连续性条件为：

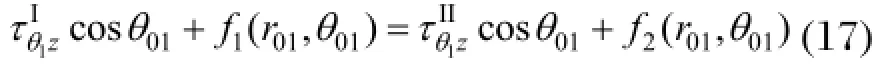
电位移连续性条件为：

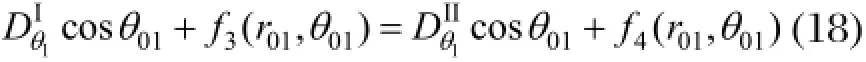
位移连续性条件为：

电位势连续性条件为：

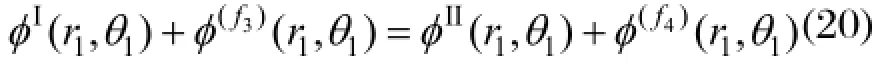
其中，

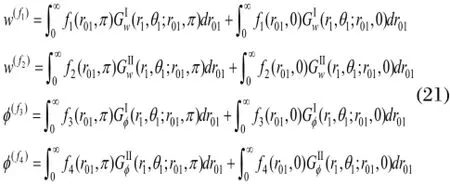
将式(15)、(16)、(21)代入(19)、(20)式并结合(17)、(18)式便可得求解未知外力系和外电场的定解积分方程：

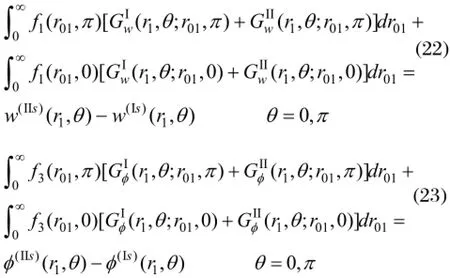
式(22)、(23)属于半无限域上含弱奇异性的第一类Fredholm型积分方程，本文采用直接离散法并结合散射波的衰减特性对其进行求解。

4 算例和分析

当剖分面上附加外力系和外电场的值求得以后，便可写出陶瓷中的总位移场和总电位势场，代入本构方程中可得陶瓷Ⅰ中圆孔周边的周向剪切应力为：

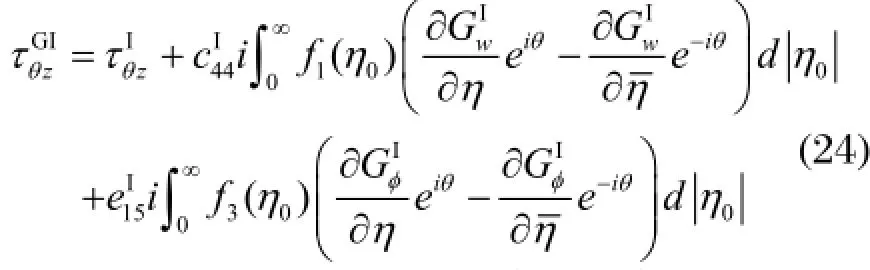
陶瓷Ⅱ中圆孔周边的周向剪切应力为：

无量纲的动应力集中系数τ*为：

作为算例，本节将给出相应的计算结果图来讨论入射波频率、材料的几何参数和物理参数对两圆孔孔边动应力集中系数的影响。图中以和分别表示上下陶瓷中的压电综合参数，表示入射波的角度，表示无量纲波数，分别表示上下陶瓷中的密度。部分计算结果与已有文献进行了比较。

图3 圆孔1的τ*值随两孔间距离的变化Fig.3 The effect of the distance of two cavities upon theof the cavity 1

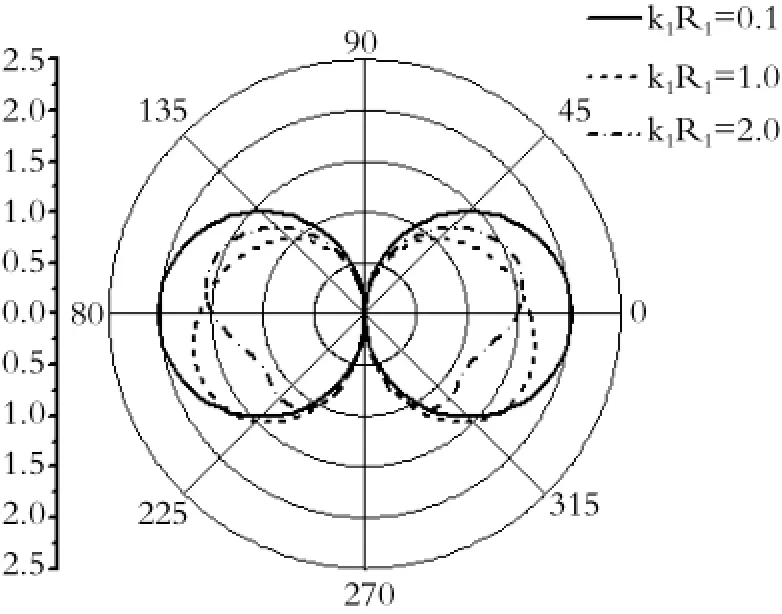
图4 圆孔1的τ*值随kIR1的变化Fig.4 The effect of the upon the of the kIR1cavity 1

(4)图8给出了λI=0.2，λII=1，h1/R1=1.5，情况下圆孔周边θ=0处的τ*值随无量纲波数kIR1和h2R1的变化。由图可见，随着无量纲波数kIR1的增大τ*值振荡衰减，且两组曲线均在低频段（kIR1＜1.0）取得最大峰值。随着h2R1的增大两组曲线取得峰值的最小距离越来越小。

(5)图9给出了λI=0.2，λII=1，R2R1=1，h1/R1=h2/R2=1.5情况下圆孔周边θ=0处的τ*值随无量纲波数kIR1和d R1的变化。从图可知，各曲线的最大峰值仍在低频段( kIR1＜ 1 .0 )取得。对于图9(a)，动应力集中系数曲线的最大值随 d R1的增大而减小，但图9(b)中却没有类似的现象。同样，随着无量纲波数 kIR1的增加 τ*值振荡衰减，这说明对于结构在低频情况下的动力学分析非常重要。

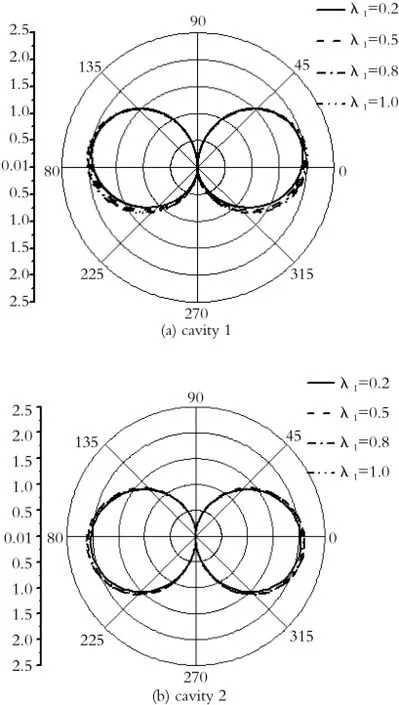
图5 圆孔的τ*值在kIR1=0.5时随压电常数的变化Fig.5 The effect of the piezoelectric constant upon theτ*of two cavities atkIR1=0.5

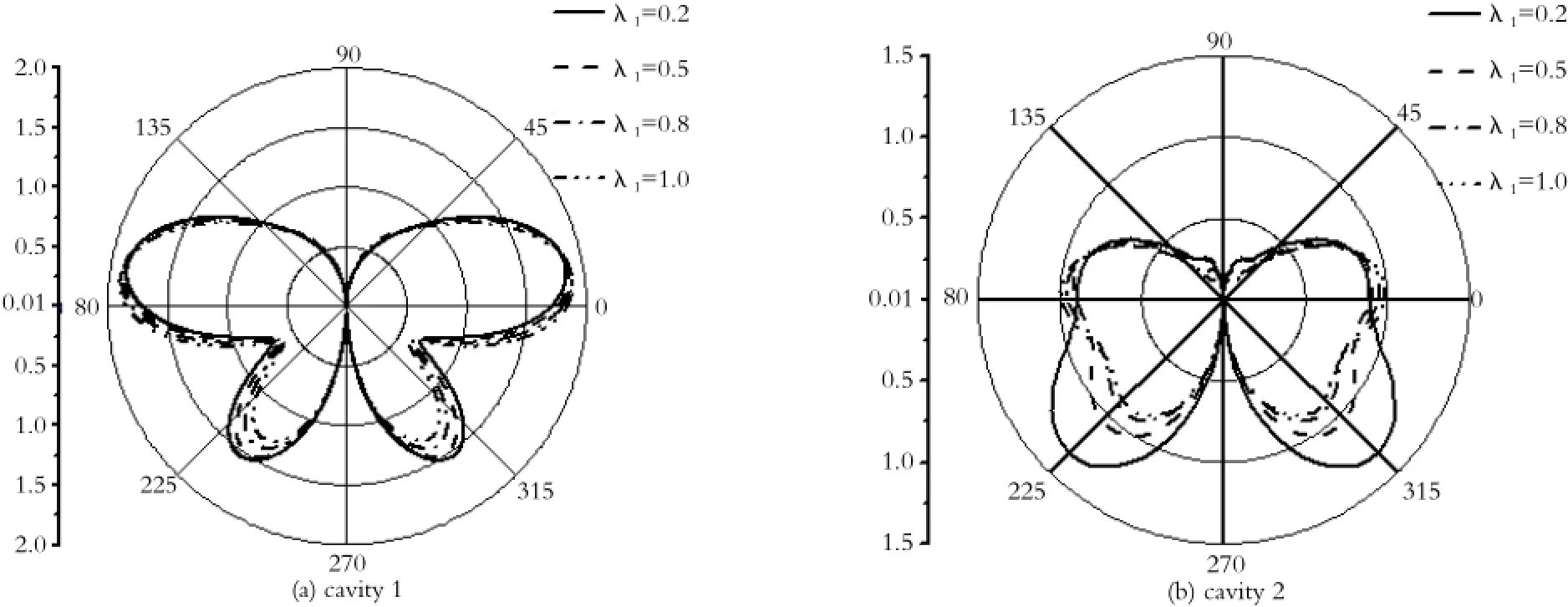
图6 圆孔的*τ值在I12.0k R=时随压电常数的变化Fig.6 The effect of the piezoelectric constant upon the*τ of two cavities atI12.0 k R=

图7 圆孔周边θ=0处的*τ值随压电常数的变化Fig.7 The effect of the piezoelectric constant upon the*τ of two cavities at θ=0

图8 圆孔周边θ=0处的*τ值随距离h2/R1的变化Fig.8 The effect of the distance of h2/R1upon the*τ of two cavities at θ=0

图9 圆孔周边θ=0处的*τ值随距离d/R1的变化Fig.9The effect of the distance of d/R1upon the*τ f two cavities at θ=0

5 结 论

本文采用Green函数方法求解了双相压电陶瓷中界面附近双圆孔对SH波散射引起的动应力集中系数。研究结果表明，入射波频率、圆心距界面的距离、两圆心距离、压电常数等参数都对孔边的动应力集中系数有影响。随着入射波频率的增大，集中系数的值一般呈现出振荡衰减的现象。因此，在低频情况下的动力学分析更为重要。一定物理参数的两压电陶瓷可以减小孔边的动应力集中。界面的存在可能增加也可能减小孔边的应力集中。因此，综合考虑压电陶瓷的物理参数和几何参数，适当选取不同的介质组合可以降低结构破坏的可能性。

[1] 方岱宁, 刘金喜. 压电与铁电体的断裂力学. 北京: 清华大学出 版社, 2008.

[2] GAO C F, FAN W X. Exact solutions for the plane problem in piezoelectric materials with an elliptic or a crack. International Journal of Solids and Structures, 1999, 25: 2527-2540.[3] LEE K L, SOH A K, FANG D N, et al. Fracture behavior of inclined elliptical cavities subjected to mixed-mode I and II electro-mechanical loading. Theoretical and Applied Fracture Mechanics, 2004, 41: 125-135.

[4] GAO C F. Influence of mechanical stresses on partial discharge in a piezoelectric solid containing cavities. Engineering Fracture Mechanics, 2008, 75: 4920-4924.

[5] Sosa Horacio, Khutoryansky Naum. New Developments Concerning Piezoelectric Materials with Defects. International Journal of Solids and Structures, 1996, 33(23): 3399-3414.

[6] CHUNG M Y, TING T C T. Piezoelectric solid with an elliptic inclusion or hole. International Journal of Solids and Structures, 1996, 33(23): 3343-3361.

[7] 周志东, 赵社戌, 匡震邦. 任意点载荷下含椭圆孔压电介质中广义应力和位移分析. 上海交通大学学报, 2004, 38(8): 1403-1407.

[8] 戴隆超, 郭万林. 压电体椭圆孔边的力学分析.力学学报, 2004, 36(2): 224-228.

[9] MEGUID S A, WANG X D. Dynamic anti-plane behavior of interacting cracks in a piezoelectric medium. Int. J. Fracture, 1998, 91: 391-403.

[10] 刘殿魁, 林宏. SH波对双相介质界面附近圆形孔洞的散射.固体力学学报, 2003, 24(2): 197-204.

[11] WANG X D. On the dynamic behavior of interacting interfacial cracks in piezoelectric media. Int. J. Solids and Structures, 2001, 38: 815-831.

[12] PAO Y H, MOW C C. Diffraction of Elastic Waves and Dynamic Stress Concentrations. New York: Crane and Russak, 1973.

Dynamic Performance of Two Circular Cavities Near the Interface in Piezoelectric Bimaterials

LI Dong1, WANG Huicong1, SONG Tianshu2
(1.Department of Civil Engineering, Hebei Jiaotong Vocational & Technical College, Shijiazhuang 050091, Hebei, China; 2. School of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China)

Based on the method of Green’s function, the problem of SH-wave scattering by two circular cavities near the piezoelectric bimaterials interface was investigated. Firstly, the displacement Green function and the electric potential Green function which were suitable for the problem were constructed by using complex variables methods and multi-polar coordinate systems. Secondly, a series of Fredholm integral equations of fi rst kind for the unknown stresses and electric fi eld could be established based on the connection condition of the interface surface. The dynamic stress concentration factor expressions around the circular cavity edge were also obtained. Finally, some examples and results for two circular cavities near the interface were given and discussed.

dynamic stress concentration factor; piezoelectric bimaterials; circular cavity near the interface; Green’s function

TQ174.75

A

1006-2874(2014)02-0018-07

2013-10-20。

2013-11-02。

Received date: 2013-10-20. Revised date: 2013-11-02.

李 冬，男，讲师，博士。

Correspondent author: LI Dong, male, Lecturer, Dr.

E-mail:lidong242@163.com