Patient-Specific Modeling in Urogynecology:A Meshfree Approach

J.B.Alford,D.C.Simkins,R.A.Rembertand L.Hoyte,MD

1　Motivation

Modern engineering analysis has led to major improvements in product design and innovation.Integrated geometric design tools,Computer Aided Design(CAD),with finite element packages are ubiquitous.Building on this success,researchers and practitioners would like to extend the application of engineering analysis to problems of existing systems,i.e.ones that were not created within a CAD system.Such domains might include forensics and reverse engineering;analysis of the natural environment;and the life sciences.An emerging area of great interest is bringing the success of engineering analysis enjoyed in product design to medicine.The goal is to be able to engineer specific medical treatments for each patient,referred to as patient-specific medicine.The common thread linking these diverse domains is that the geometry of the problem to be analyzed does not come with a ready mathematical description,as in CAD,but rather in the form of a set of discrete points.The challenge,then,is to develop an analysis-suitable description of the problem domain directly from the point set.

One option for developing an analysis-suitable geometric representation is to mesh the point set for use in finite elements,as in Fig.10.This does have some difficulties,in particular,developing a mesh that is topologically sound,i.e.does not intersect or overlap,does not have holes or gaps,etc.can be quite difficult.In practice,an analyst often must manually assist in the meshing process.Such efforts are often time-consuming and expensive in human time.Efforts have been made to automate the task of generating quality finite element meshes for complex geometry with some success.Generic template meshes have been mapped to patient specific geometry in order to curtail human effort[Salo,Beek,and Whyne(2013),Baghdadi,Steinman,and Ladak(2005)and Bucki,Lobos,and Payan(2010)].Yet simulating large deformations proves troublesome for these meshes.

Another option is to avoid generating such a quality mesh by using a mesh free method.The computation of mesh free shape functions requires that each point be associated with a compact support and that the compact supports overlap such that they cover the domain.Each point must also associate with a portion of volume.Many of the proposed methods for computing particle volume and supports rely on Voronoi diagrams or other mesh concepts.Generating such diagrams can be expensive in,so avoiding them is crucial in developing an automatic and efficient method.

We propose a new method based on a mesh free Galerkin formulation,in particular the Reproducing Kernel Particle Method(RKPM).In the mesh free method,no mesh is required for the analysis,and hence the troubles of meshing are avoided.Some implementations of mesh free methods still use a background mesh for in-tegrating the weak form,but this mesh is not required to meet the more rigorous standards demanded by finite elements,and hence,can be generated fairly easily.The crux of the algorithm is the determination of the particle distribution,particle interactions,support size and representative volume associated with each particle.

2　Background

The female pelvic floor muscles form a complex structure that is responsible for supporting the pelvic organs such as rectum,vagina,bladder,and uterus.These muscles and associated connective tissues are ultimately anchored to the bony pelvic scaffold,and play a major additional role in maintaining continence of urine and bowel contents,while allowing for important physiologic activities like urination,defecation,menstrual flow,and biomechanical processes like childbirth and sexual intercourse.

The major components of the pelvic floor are outlined in Fig.1(a)and Fig.1(b).A thorough description of the functional anatomy of the female pelvic floor can be found in[Ashton-Miller and DeLancey(2007)],[Hoyte and Damaser(2007)]and[Herschorn(2004)].The levator ani muscle group,as shown in Fig.1(b)is the ultimate supporting structure responsible for holding organs in the body,and is rightfully the main focus of most studies regarding pelvic floor dysfunction[Hoyte,Schierlitz,Zou,Flesh,and Fielding(2001),[Venugopala Rao,Rubod,Brieu,Bhatnagar,and Cosson(2010)],[Lien,Mooney,DeLancey,and Ashton-Miller(2004)].The vagina,Fig.1(c),is suspended across the pelvis,and is anchored,in large part to the levator ani,and less so,the Obturator internus muscles.The vagina,in turn,supports the bladder,and works with the levator ani to keep the rectum in a position appropriate for fecal continence at rest,and bowel evacuation when appropriate.

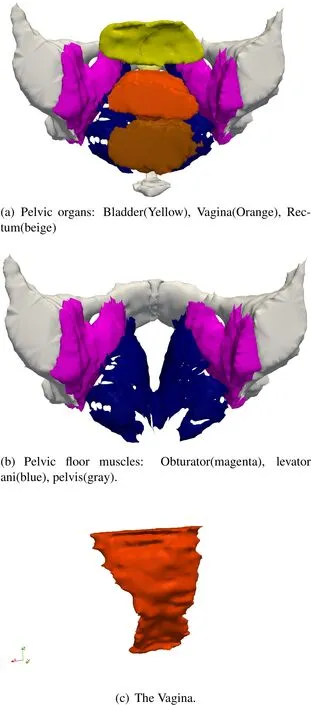
Figure 1:Major components of the female pelvic floor

Many finite element studies have been produced of the levator ani muscles ranging from shell element models to full volume element models[Hoyte,Damaser,War field,Chukkapalli,Majumdar,Choi,Trivedi,and Krysl(2008)],[Martins,Pato,Pires,Jorge,Parente,and Mascarenhas(2007)],[Noritomi,da Silva,Dellai,Fiorentino,Giorleo,and Ceretti(2013)].These models have been valuable tools in learning about the mechanics of the pelvic floor,but many of the models focus solely on the levator ani,without considering the interaction between the other pelvic structures.To help address this deficit,focus is placed on the vagina for the examples in this paper.Since a mesh is required for finite element analysis,the geometry is often idealized,both due to the piece-wise polyhedral approximation and the need to make adjustments to the points to create a quality mesh.Our aim is to accurately represent the geometry and produced studies involving multi-component interactions.In[Doblaré,Cueto,Calvo,Martínez,Garcia,and Cegoino(2005)],the prospects of performing meshfree analysis for biomechanics problems is discussed with several Galerkin methods being described.They chose to use the natural element method which is closely tied to Voronoi diagrams,on the basis that essential boundary conditions are easily applied.The ease of applying the essential boundary conditions comes at the cost of generating a mesh of the domain,though the authors say the mesh generation requires no interaction with the user.They showed successful examples involving mostly bony tissue and some cartilage.Meshfree methods have been used successfully in other areas of biomechanics including the heart[Liu and Shi(2003)],and the brain[Horton,Wittek,Joldes,and Miller(2010)],[Miller,Horton,Joldes,and Wittek(2012)].In a similar vein,a hybrid meshfree-mesh-based method based on the Reproducing Kernel Element Method(RKEM)was undertaken in[Simkins,Jr.,Kumar,Collier,and Whitenack(2007)and Jr.,Collier,Juha,and Whitenack(2008)].RKEM details can be found in[Liu,Han,Lu,Li,and Cao(2004).Li,Lu,Han,Liu,and Simkins,Jr.(2004),Lu,Li,Simkins,Jr.,Liu,and Cao(2004)and Simkins,Jr.,Li,Lu,and Liu(2004)].

3　RKPM

The problem domain is discretized by a collection of particles,each representing a certain volume and mass of material.A functionfde fined on the domain is approximated by an expression

whereis a smooth kernel function,andis an approximation operator.In RKPM,the form of the kernel is chosen to be

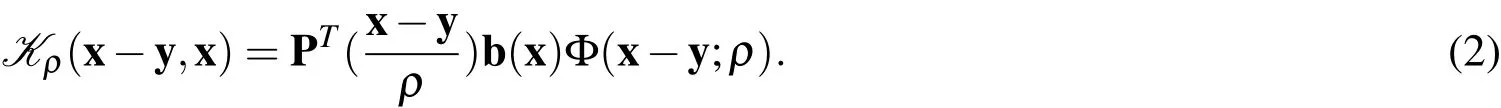
The parameterρis called the smoothing length and is the characteristic length scale associated with each particle.The window function Φ is a non-negative,smooth function that is compactly supported with support radius of lengthρ.The vector P contains the monomial terms of a polynomial of some order.In the present work,a tri-linear basis is used,so

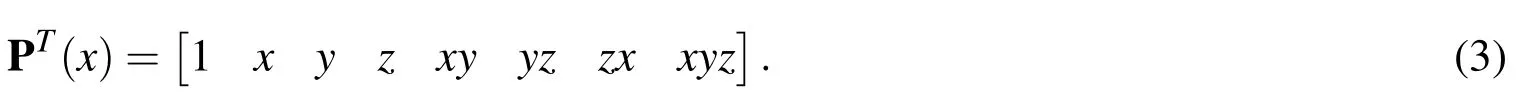
Finally,the vector b,which we term the normalizer,is computed at each evaluation point as a correction function to enforce consistency conditions on the approximation.The consistency conditions lead to a set of equations

whereαis a multi-index withUpon substituting Eq.2,leads to the following set of linear equations

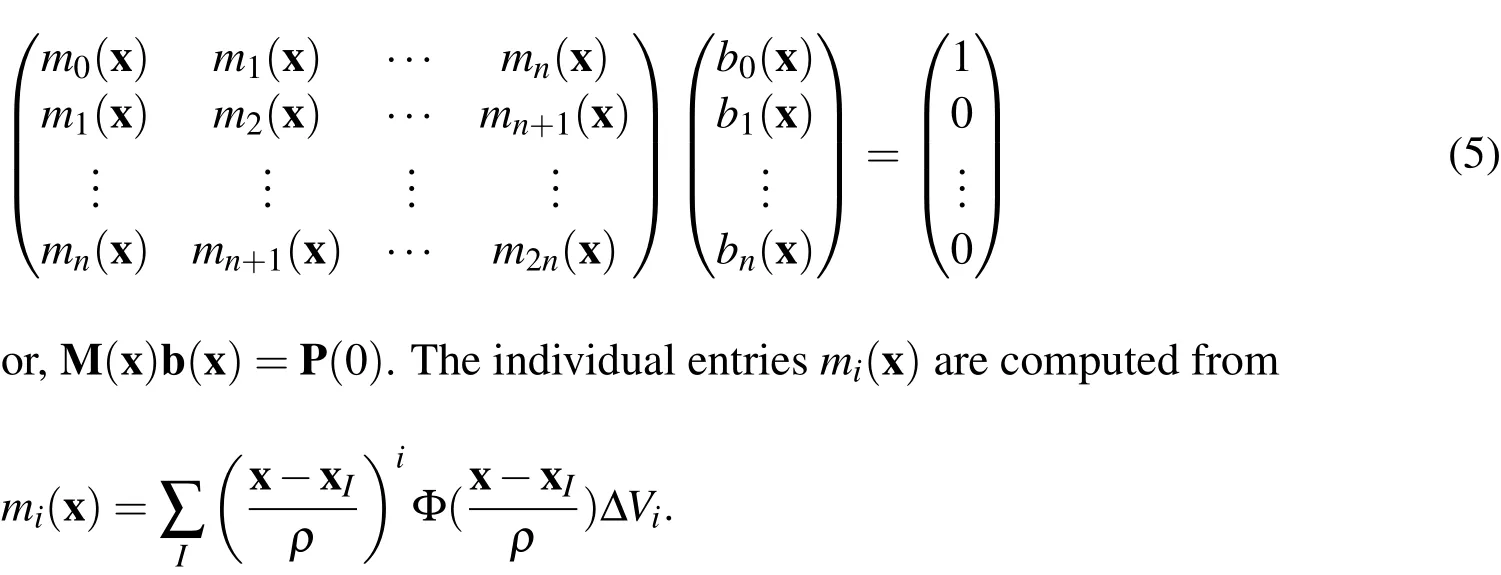
The system Eq.5 is called the moment equation whose solution yields the values for the normalizer b(x).The present work is based upon the observation that the actual domain is de fined where the moment matrix is non-singular.Conversely,where the moment matrix is singular,there is no body.

4　Overall process

Readily available programs,such as the 3D Slicer(www.slicer.org),can read the data generated by the imaging machines,convert the images to point clouds,and generate meshes.This is not quite a satisfactory result,because the resulting images,while visually appealing,do not stand up under the scrutiny required for analysis.In particular,the meshes generally have duplicate points,edges and faces;holes and discontinuities;and topological variations such as intersecting faces.The first of these problems can easily be rectified,but the latter problems generally require manual intervention to guide software in repairing the mesh.

Meshfree Galerkin methods build their function spaces directly from point sets,and thus are not plagued by the same issues as mesh-based methods.This feature makes meshfree methods attractive for life science applications.The basic approach we follow is:

目前国内外对PUE指标还没有统一的分级标准，国内电网企业在运行的数据中心PUE值基本在2～3之间[8]，国内较为节能新建数据中心一般在1.6～1.8，而国外最先进的绿色数据中心PUE值甚至在1.2以下，但采用了多种极端的节能手段，在国内电网企业中未必适合。通过能效测量、计算与统计，可有效地衡量电网企业数据中心的能源成本，指导数据中心的能效管理，优化数据中心的能源效率。根据目前国内数据中心的一般情况，若统计出PUE值大于2.0，则属于偏高水平，有较大的优化空间[9]，从而可使用多种方法改进数据中心的能效水平，如：

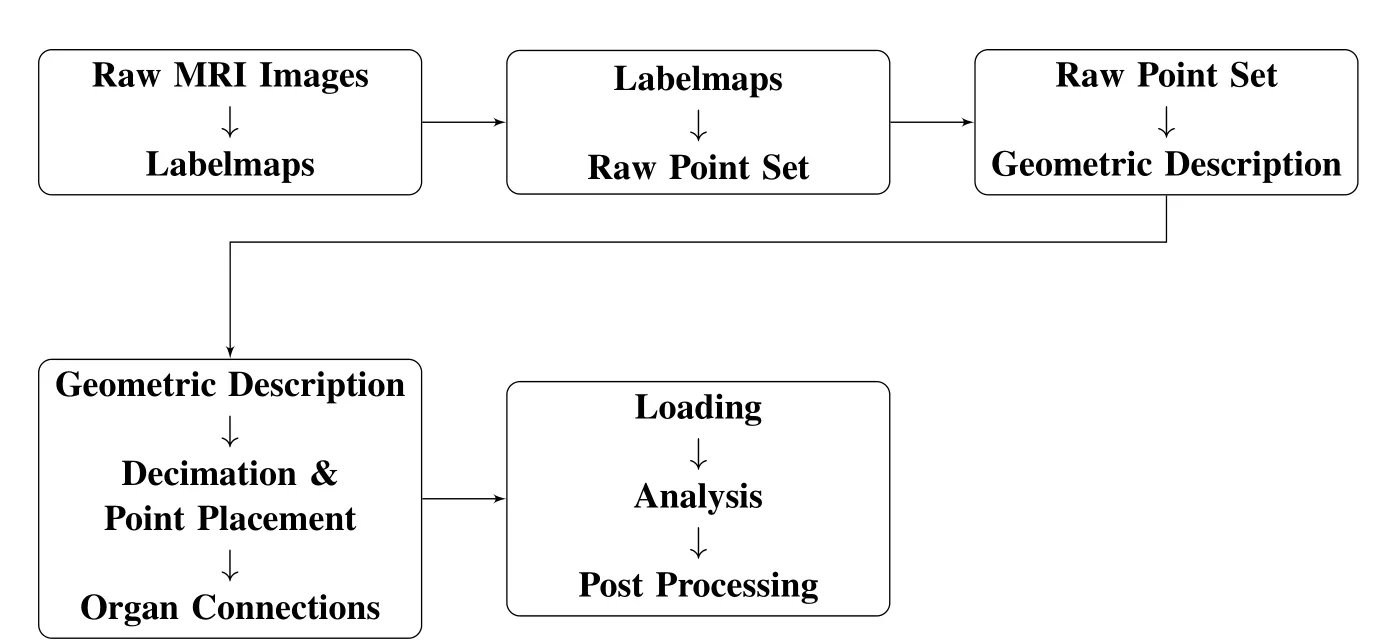
Figure 2:Algorithm outline

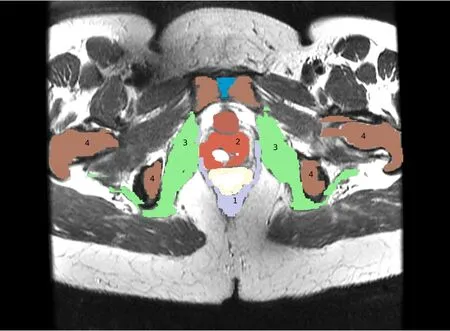
Figure 3:Labeled Image.(1)Levator ani,(2)Vagina,(3)Obturator,(4)Pelvis

A patient speci fic model is created first by producing a sequence of images of the pelvic fl oor via some method such as magnetic resonance imaging,MRI.In these raw images the various organs and tissues are not distinguished,in order to segregate the organs into individual models the images must be segmented as in Fig.3.The resulting image is called a labelmap.Automatic segmentation is an open research topic,currently the images are at least partially segmented by hand.Some methods for segmenting the pelvic floor are discussed in[Ma,Jorge,Mascarenhas,and Tavares(2012)].After the labelmaps are generated,the discrete point set representation of the models are produced.The images are integer arrays with each index referring to a pixel,or color value.Each pixel is representative of an area with pre-de fined dimensions.When the labelmaps are stacked,the space between consecutive images is represented with voxels,or volume elements.The voxels are transformed into the raw point set inbased on their dimensions and location in image space.The raw point set is then used to reconstruct the continuous geometry of the object via an implicit representation described in§5.The reconstructed geometry is an adequate description of the domain that is useful for placing RKPM analysis suitable particles as warranted.Then constructing a decimated point set for the purpose of analysis can be accomplished by generating a regular grid of points and eliminating any points not in the domain.Figure 4 shows the sequence of progression from the raw point set in Fig.4(a)to the decimated point set in Fig.4(c).The volume reconstructed from the raw point set is shown in Fig.4(b).Once all of the organs of interest are processed and have their final points placed in their respective domains,any organs that will interact during the simulation must be connected.The current method is to model connective tissue as linear springs between organs.After the organs are connected any applicable loading conditions and essential boundary conditions are applied.

5　Geometric Description

The initial geometry is obtained from a discrete point set,thus the continuous geometry must be reconstructed.As discussed earlier,the moment matrix in Eq.5 is non-singular inside of the domain.The linear dependence of the moment equations is based largely on the number of particles in the support and the spatial distribution of these particles.If properly constructed,the moment matrix is well-conditioned and invertible everywhere in a domain.The moment equations quickly become linearly dependent as the limits of the domain are approached.We now use this fact to build a function to describe the geometry implicitly.In numerical linear algebra,thecondition numberof a matrix is a measure of“how singular”a matrix is.The condition number is defined[Saad(2003)]as

Figure 4:Geometry reconstruction and point decimation of a vagina model

The best conditioned matrix hasκ=1,a singular matrix hasκ→∞.Therefore we can define our geometry based on the condition number of the system of equations:

Where M(x)is the moment matrix at a point andκ,is a function returning the condition.Notice that in Eq.7 the reciprocal condition number is used and the range of the function is(0,1],withκ−1=0 indicating a singular matrix.Then the reconstructed domain is de fined as:

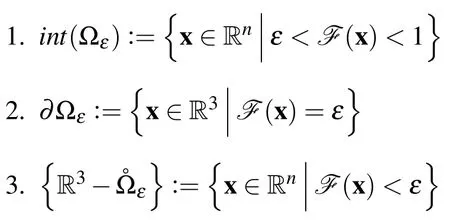
Where 1 is the interior and 2 is the boundary of the domain andεis small.With this definition,the boundary of the domain is defined as a contour of Eq.7.The shape of the reconstructed boundary can be controlled through the radius of support.As the support radius grows any surface features are smoothed over,conversely as the support radius is decreased any surface features become more sharply defined.

The set of points derived from the image Xi,are the discrete representation of the domain,Ω.Developing a meshfree function space directly from a general point set is a non-trivial task due to the need for accurate integration weights and support radius.The set of points can actually be thought of as the vertices of a hexahedral mesh that is usually referred to as the voxel model.Appropriate representative particle volume ∆VI,and support radiusρcan be assigned using data from the voxel elements.Due to aliasing artifacts the voxel mesh is not suitable for representing the smooth geometry of biological tissue,and it would not generate a smooth solution to the PDE’s if used for a finite element model.Yet,by using the vertices to construct a meshfree representation of the geometry,the representation is smooth.The objects of interest in the pelvic floor are smooth,not rough.One critique of the proposed method is that it may not represent the actual geometry precisely enough.On the other hand,a voxel mesh,as in Fig.5,is clearly not a smooth body,and itself is inaccurate due to the aliasing and rough discretization inherent in a digital medical image.Refer back to Fig.1(c)for an example of a smooth representation.A detailed study and quantification of this issue is the subjectof an upcoming paper.

Figure 5:Voxel mesh representation of the vagina

5.1　Example in 1D

In order to illustrate this definition of the geometry,a one dimensional example is plotted over a unit domain.The domain is discretized with ten particles and their integration weights are assigned as described in[Li and Liu(2004)].The particles are uniformly distributed throughout the domain,so a suitable support radius is defined as

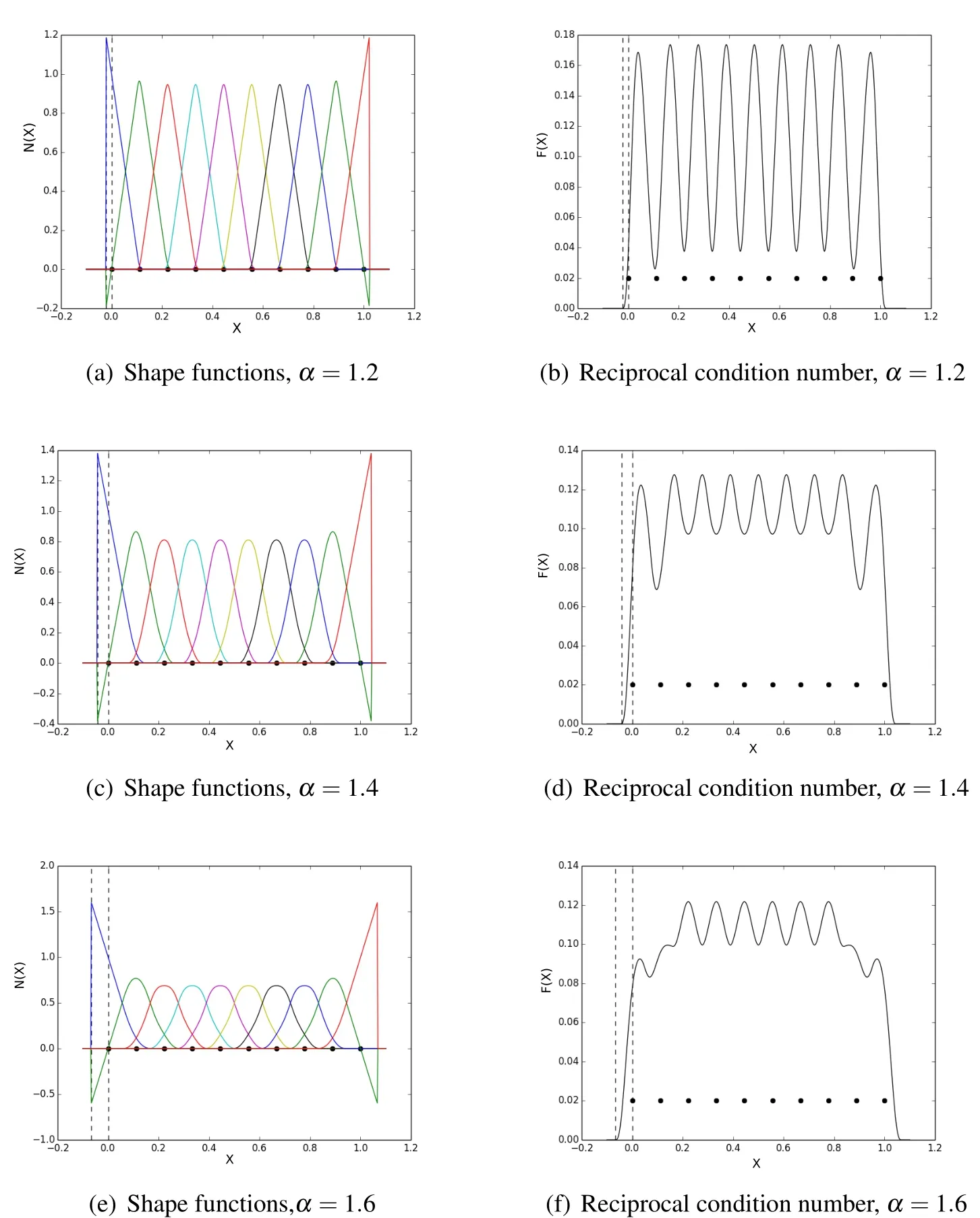
Figure 6:1D Shape functions and reciprocal condition number

where ∆x is the particle spacing andαis the dilation coefficient.The shape functions and the corresponding geometry representation are shown for dilation coefficient values of 1.2,1.4and1.6.The dashed vertical lines in Fig.6 are bounds for the area starting at the first boundary particle and extending out until the moment matrix is singular to machine precision.This area will be referred to as therindof the reconstructed domain.Notice that as the dilation coefficient is increased this rind grows in size.This would correspond to a smoothing of geometric features,which might or might not be desirable.The shape functions plotted in Fig.6 show the correlation between support coverage and moment matrix condition.As a reminder,the moment matrix is computed via nodal integration,each term in the summation is a rank one matrix representative of a particles contribution.If this integral is dominated by a single term,the overall condition of the moment matrix is poor,conversely when each of the terms are equally weighted the moment matrix is well conditioned.This shows up in Fig.6(b),Fig.6(d),and Fig.6(f)as the fluctuations in.In Fig.6(b),these fluctuations are much greater than in the in Fig.6(d)and Fig.6(f).The peaks are higher between particles,indicating a well conditioned moment matrix and no dominating term in the integral,and the valleys are much lower at a particle,indicating a poorly conditioned moment matrix and thus one term in the integral is dominating.Since we are choosing the surface based on some threshold valuethese fluctuations could cause trouble if the functions falls belowεin an undesirable location.This could result in holes in the domain where none exist.A safe method for representing sharp surface features,meaning using a small value forα,is to increase the dilation coefficient of internal particles while keeping the boundary particle dilation coefficients the same as in Fig.7.This method minimizes the size of the rind,while smoothing the fluctuations in

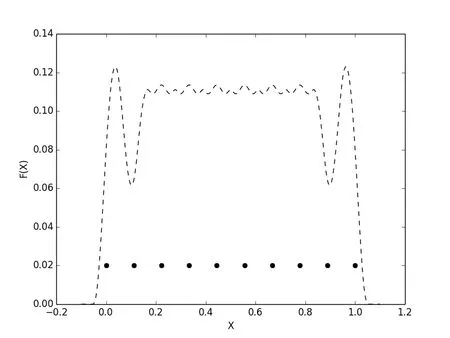
Figure 7:Reciprocal condition number:boundary particles α=1.2,interior particles α=1.5

Increasing the number of particles in the domain would also remedy this problem,yet by simply controlling the dilation parameter we can can get the same effect without adding more degrees of freedom.

5.2　Example in 3D

The ideas discussed in one dimension hold true for three dimensional models.A volume rendering of the vagina is shown in Fig.8(a),the plane slicing through the model shows the location of the plot in Fig.8(b).Fig.8(c)shows the moment matrix reciprocal condition number is then plotted over the line drawn across the middle of Fig.8(b).The top portion of the model is essentially a thin walled tube,and this shows up in the line plot across the body as two peaks in the function.The second peak shows the same fluctuations that were discussed in the one dimensional example.

In order to perform an analysis in an efficient manner,it is important to limit the number of particles in the model.Since the goal of the method is to maintain patient specific features in the model,we need to show that decimation of the model does not significantly alter the geometry we are representing.The images in Fig.9 depict the volume renderings for three different particle sets.The first representation with 112,128 particles,Fig.9(a)is derived directly from a medical image.The volume rendering of this representation,Fig.9(b)has well defined features such as the indentation of the front wall and the ridges along the side walls.The raw point representation was decimated to 26,809 particles,shown in Fig.9(c).The volume rendering for this representation still has the well defined indentation and the ridges on the side wall are still defined.The third representation in Fig.9(e),has a particle count of 3,339.While this representation retained the overall shape of the original model,the indentation on the front wall and the ridges on the side wall are not as well defined.The tetrahedral Finite Element mesh in Fig.10 shows some of the same geometric features as our volume reconstructions,yet the surface is not smooth.

6　Application Example

We seek to develop a computer simulation to perform virtual studies of mechanical problems involving the pelvic floor.Ultimately,the goal is to provide an automatic,or nearly automatic,process to perform engineering analysis on objects defined by medical images.Vaginal contraction was chosen as the first test case because it is simpler than a full childbirth simulation,yet has direct relevance to actual medical procedures and involves all aspects of the computational problems we seek to address.Vaginal contraction is a long term side effect of pelvic radiation therapy and is caused by the development of scar tissue.This scar tissue results in a shortening and narrowing of the vagina and has associated difficulties and treatments as described in[Bruner,Lanciano,Keegan,Corn,Martin,and Hanks(1993)]and[Decruze,Guthrie,and Magnani(1999)].

For the present study,the vagina,obturator and pelvis are the organs under consideration.In order to model vaginal contraction,a-2.5%strain was applied to the vagina over a series of seven static load steps,leading to a large overall decrease in width and length.The lateral vaginal wall was attached to the Obturator internus via linear springs,and the Obturator internus was anchored to the pelvic bones via essential boundary conditions.For simplicity the cervix was modeled as a fixed rigid body and the vagina was connected to it via linear springs.The organs were discretized with 16119,17691,and 18553 particles for the vagina,left obturator and right obturator,respectively.The original undeformed con figuration is shown in Fig.11.The distortional strain is plotted on the final con figuration in Fig.12.

Figure 8:Vagina plots

Figure 9:Decimation of vagina model:112,128 particles→26,809 particles→3,339 particles

Figure 10:Finite Element mesh of the vagina

Figure 11:Original Con figuration

Figure 12:Distortional strain plotted on final con figuration.

7　Conclusion

An algorithm for completely automated generation of analysis-suitable geometries from discrete point sets was presented.The method appears to work well on organs found in the female pelvic floor and comparisons were made to voxel mesh geometries.Finally,to demonstrate that the resulting geometry is analysis-suitable,a simulation of vaginal contracture was performed and presented using the geometry representation from the algorithm.

Ashton-Miller,J.A.;DeLancey,J.O.L.(2007):Functional anatomy of the female pelvic floor.Annals of the New York Academy of Sciences,vol.1101,no.1,pp.266–296.

Baghdadi,L.;Steinman,D.A.;Ladak,H.M.(2005):Template-based finite-element mesh generation from medical images.Computer Methods and Programs in Biomedicine,vol.77,no.1,pp.11–21.

Bruner,D.W.;Lanciano,R.;Keegan,M.;Corn,B.;Martin,E.;Hanks,G.E.(1993):Vaginal stenosis and sexual function following intracavitary radiation for the treatment of cervical and endometrial carcinoma.International Journal of Radiation Oncology*Biology*Physics,vol.27,no.4,pp.825–830.

Bucki,M.;Lobos,C.;Payan,Y.(2010):A fast and robust patient specific finite element mesh registration technique:Application to 60 clinical cases.Medical Image Analysis,vol.14,no.3,pp.303–317.

Decruze,S.;Guthrie,D.;Magnani,R.(1999):Prevention of vaginal stenosis in patients following vaginal brachytherapy.Clinical Oncology,vol.11,no.1,pp.46–48.

Doblaré,M.;Cueto,E.;Calvo,B.;Martínez,M.;Garcia,J.;Cegoñino,J.(2005):On the employ of meshless methods in biomechanics.Computer Methods in Applied Mechanics and Engineering,vol.194,no.68,pp.801–821.

Herschorn,S.(2004):Female pelvic fl oor anatomy:the pelvic fl oor,supporting structures,and pelvic organs.Reviews in urology,vol.6,no.Suppl 5,pp.S2.

Horton,A.;Wittek,A.;Joldes,G.R.;Miller,K.(2010):A meshless Total Lagrangian explicit dynamics algorithm for surgical simulation.INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN BIOMEDICAL ENGINEERING,vol.26,no.8,pp.977–998.

Hoyte,L.;Damaser,M.S.(2007):Magnetic resonance-based female pelvic anatomy as relevant for maternal childbirth injury simulations.Annals of the New York Academy of Sciences,vol.1101,pp.361.

Hoyte,L.;Damaser,M.S.;War field,S.K.;Chukkapalli,G.;Majumdar,A.;Choi,D.J.;Trivedi,A.;Krysl,P.(2008):Quantity and distribution of levator ani stretch during simulated vaginal childbirth.American Journal of Obstetrics and Gynecology,vol.199,no.2,pp.198.e1–198.e5.

Hoyte,L.;Schierlitz,L.;Zou,K.;Flesh,G.;Fielding,J.R.(2001):Twoand 3-dimensional mri comparison of levator ani structure,volume,and integrity in women with stress incontinence and prolapse.American Journal of Obstetrics and Gynecology,vol.185,no.1,pp.11–19.

Jr.,D.C.S.;Collier,N.;Juha,M.;Whitenack,L.B.(2008):A framework for studying the rkem representation of discrete point sets.In Griebel,M.;Schweitzer,M.A.(Eds):Meshfree Methods for Partial Differential Equations IV,volume 65 ofLecture Notes in Computational Science and Engineering,pp.301–314,Berlin.Springer-Verlag.

Li,S.;Liu,W.K.(2002):Meshfree and particle methods and their applications.Applied Mechanics Review,vol.55,no.1,pp.1–34.

Li,S.;Liu,W.K.(2004):Meshfree Particle Methods.Springer,Berlin.

Li,S.;Lu,H.;Han,W.;Liu,W.K.;Simkins,Jr.,D.C.(2004):Reproducing kernel element method,Part II.Global conformingIm/Cnhierarchy.Computer Methods in Applied Mechanics and Engineering,vol.193,pp.953–987.

Lien,K.-C.;Mooney,B.;DeLancey,J.O.L.;Ashton-Miller,J.A.(2004):Levator ani muscle stretch induced by simulated vaginal birth.Obstet Gynecol.,vol.103(1),pp.31–40.

Liu,H.;Shi,P.(2003):Meshfree representation and computation:Applications to cardiac motion analysis.In Taylor,C.;Noble,J.(Eds):Information Processing in Medical Imaging,volume 2732 ofLecture Notes in Computer Science,pp.487–498.Springer Berlin Heidelberg.

Liu,W.;Jun,S.;Zhang,Y.(1995):Reproducing kernel particle methods.International Journal for Numerical Methods in Fluids,vol.20,pp.1081–1106.

Liu,W.K.;Han,W.;Lu,H.;Li,S.;Cao,J.(2004):Reproducing kernel element method:Part I.Theoretical formulation.Computer Methods in Applied Mechanics and Engineering,vol.193,pp.933–951.

Lu,H.;Li,S.;Simkins,Jr.,D.C.;Liu,W.K.;Cao,J.(2004):Reproducing kernel element method Part III.Generalized enrichment and applications.Computer Methods in Applied Mechanics and Engineering,vol.193,pp.989–1011.

Ma,Z.;Jorge,R.N.M.;Mascarenhas,T.;Tavares,J.M.R.(2012):Segmentation of female pelvic cavity in axial t2-weighted mr images towards the 3d reconstruction.International Journal for Numerical Methods in Biomedical Engineering,vol.28,no.6-7,pp.714–726.

Martins,J.A.C.;Pato,M.P.M.;Pires,E.B.;Jorge,R.M.N.;Parente,M.;Mascarenhas,T.(2007):Finite element studies of the deformation of the pelvic fl oor.Annals of the New York Academy of Sciences,vol.1101,no.1,pp.316–334.

Miller,K.;Horton,A.;Joldes,G.;Wittek,A.(2012):Beyond finite elements:A comprehensive,patient-specific neurosurgical simulation utilizing a meshless method.Journal of Biomechanics,vol.45,no.15,pp.2698–2701.

Noritomi,P.;da Silva,J.L.;Dellai,R.A.;Fiorentino,A.;Giorleo,L.;Ceretti,E.(2013):Virtual modeling of a female pelvic floor and hypothesis for simulating biomechanical behavior during natural delivery.Procedia{CIRP},vol.5,no.0,pp.300–304.First{CIRP}Conference on BioManufacturing.

Nygaard,I.;Barber,M.D.;Burgio,K.L.;et al(2008):Prevalence of symptomatic pelvic floor disorders in us women.The Journal of the American Medical Association,vol.300,no.11,pp.1311–1316.

Saad,Y.(2003):Iterative Methods for Sparse Linear Systems:Second Edition.Society for Industrial and Applied Mathematics(SIAM,3600 Market Street,Floor 6,Philadelphia,PA 19104).

Salo,Z.;Beek,M.;Whyne,C.M.(2013):Evaluation of mesh morphing and mapping techniques in patient specific modeling of the human pelvis.International Journal for Numerical Methods in Biomedical Engineering,vol.29,no.1,pp.104–113.

Simkins,Jr.,D.C.;Kumar,A.;Collier,N.;Whitenack,L.(2007):Geometry representation,modification and iterative design using RKEM.Computer Methods in Applied Mechanics and Engineering,vol.196,pp.4304–4320.

Simkins,Jr.,D.C.;Li,S.;Lu,H.;Liu,W.K.(2004):Reproducing kernel element method Part IV.Globally compatibleCn(n≥1)triangular hierarchy.Computer Methods in Applied Mechanics and Engineering,vol.193,pp.1013–1034.

Venugopala Rao,G.;Rubod,C.;Brieu,M.;Bhatnagar,N.;Cosson,M.(2010):Experiments and finite element modelling for the study of prolapse in the pelvic floor system.Computer Methods in Biomechanics and Biomedical Engineering,vol.13,no.3,pp.349–357.PMID:20099169.