Geometrical Modeling of Cell Division and Cell Remodeling Based on Voronoi Tessellation Method

Liqiang LinXianqiao Wangand Xiaowei Zeng

1　Introduction

Muscle tissue,epithelial tissue,connective tissue and nerve tissue are the four major tissue types in a vast array of metazoans[Cowin and Doty(2007)].From a fertilized egg to an embryo,the growth of metazoan happens in the development of all kinds of tissues.Development of biological tissue generally has three distinct processes,e.g.growth,remodeling and morphogenesis[Garikipati et al.(2004)].

Comprehensive overview about the biomechanics of growing tissues can be found in an excellent review by Taber[Taber(1995)].From the microscopic level,tissues are composed of cells and extracellular matrix.Clearly,tissue growth can occur either through the proliferation of new cells or by the production of extracellular matrix[Jones and Chapman(2012)].There is considerable evidence that the cell proliferation and the spatial arrangement of cells during development play a key role in the tissue-level morphogenesis shape[Baena-López et al.(2005);Lecuitand Lenne(2007);Resino et al.(2002)].Studies on critical features of tissue homeostasis show that normal tissue growth and renewal is dependent on the positioning of the cell division axis[Théry and Bornens(2006)].Most of the cell proliferation is in the epithelial tissue and around 80%of human cancers progress at epithelial sheets[Alberts(2008);Jones and Chapman(2012)],which results in a popularity of research into epithelial tissue.In epithelial tissues,cells are packed together closely[Braga(2000);Hildebrand(2005)],which is different from cell dispersion in connecting tissue[Tomasek et al.(2002)].The behavior of cell ensembles is widely studied by the cell-based models,such as epithelial mono-layers[Brodland et al.(2007)],multi-cell spheroids[Schaller and Meyer-Hermann(2005)],and Dictyostelium discoideum slug[Dallon and Othmer(2004)].Considering a flat and monolayer epithelial tissue,the images of cells consisting of epithelial tissue show polygonal or polyhedral structures[Dubertret and Rivier(2000);Gibson et al.(2006);Meineke et al.(2001)].Based on polygonal shape of epithelial cell,Dirichlet domains were employed to describe polyhedral cellular patterns and cell division for a piece of rat intestine[Honda(1978)].The weighted Voronoi tessellation was utilized to model the cell shape and simulate the process of increasing large cell number[Honda et al.(2000)].Meanwhile,cells are represented as polygons by vertex dynamics models to study the in fl uence of cell mechanics,cell-cell interaction and proliferation on epithelial packing[Farhadifar et al.(2007)].Vertex dynamics models has also been used to simulate cell behavior underlying tissue convergence and extension[Weliky et al.(1991)],and to study cell rearrangements by accounting for the balance of forces between neighboring cells within an epithelium[Weliky and Oster(1990)].Cell movement and arrangement has been studied on the two-dimensional cellular organization of the intestinal crypt by using offlattice Voronoi model[Meineke et al.(2001)].

Despite that epithelial cell behavior has been studied widely,very little is known about the possible implications of cell pattern geometry for mechanical properties of tissues or key biological processes,such as planar polarization,cell division and tissue remodeling[Gibson and Gibson(2009)].Thus,cell division and cell-cell interactions also lead to a great deal of interests.The main objective of our present work is to simulate the cell division and remodeling based on Voronoi tessellation method.This work is a preliminary study,and we only investigate the geometric cell proliferation and remodeling(not including cell mechanics and cell-cell interactions).

2　Methodology

2.1　Halton sequence

In statistics,the most prominent type of quasi-random number sequences has been the Halton sequences[Chi et al.(2005);Halton(1960)]Halton sequence is designed to generate points in unit space(0−1space)for numerical methods such as Monte Carlo simulations.In one dimension,to generate a sequence ofNinteger numbers,the standard Halton sequence is used by taking a prime numberpr(pr≥2),and locating the sequence ofNintegers 1,2,3,···,n,···Nin terms of the basepr[Bhat(2003);Hess and Polak(2003)]:

wheremis an index of the power to which the base is raised andM=logpr(n)=ln(n)/ln(pr).Heren(n=1,2,···,N)can be represented in digitized form in radixprnotation as:nMnM−1···n1n0.By reversing the order ofn(n=1,2,···,N),the Halton sequence in the prime basepris obtained lying in the unit space(between 0 and 1)[Halton(1960)]:

Based on Halton sequence method,it is easy to generate quasi-random point distribution in a unit plane.Take prime number 2 as an example,the first element of the Halton sequence is:Now take each of the two parts and divide them into 2 parts again.The dividing points constitute the next elements in the Halton sequence:andBy this procedure,we can get a series of Halton sequence as following:Similar sequences are defined for other numbers,such as prime

In two-dimensional(2D)space,a point in the space should have two coordinates,xandy.If we set prime 2 as Halton sequence base alongxaxis and 3 as Halton sequence base alongyaxis.For instance,the Fig.1 illustrates the two-dimensional distribution of 64 Halton sequence points.

2.2　Voronoi tessellations

Figure 1:Distribution of Halton sequence points in 2D space.

whereXzirepresent the coordinates of kernel pointi;d(Xzi,X)denotes the Euclidean distance betweenXziandX;Xbelonging to Voronoi region ofis closer to generatorthan other generators,as shown in Fig.2.

If a density functionρ(X)≥0 de fined on domain Ω is given,then for each Voronoi regionVi,the mass centroid ofofVican be de fined as:

Figure 2:Schematic of Voronoi diagram.

In the case of,this Voronoi tessellation is called as centroidal Voronoi tessellation.Generally,an arbitrary choice of generating pointsin a region is not the mass centroids of the corresponding Voronoi regions initially from Halton sequence distribution.Fig.3 shows the Voronoi tessellation using 64 Halton sequence points of section 2.1 as generators and the densityρ(X)=1.

Figure 3:The Voronoi regions corresponding to 64 Halton sequence points in a unit square.

2.3　Probabilistic Lloyd’s method

In order to determine the centroidal Voronoi tessellation,there are many methods to obtain the center point of Voronoi region,such as MacQueen’s method and Lloyd’s method[Linde et al.(1980);Lloyd(1982);MacQueen(1967)].Here,a modi fied Lloyd’s method is employed through probabilistic theory.This modified Lloyd’s method is based on probabilistic method and is viewed as probabilistic Lloyd’s method.Given a region Ω and a density functionρ(X)≥0 de fined for allX∈Ωto generateninitial generators then the procedure is as following:

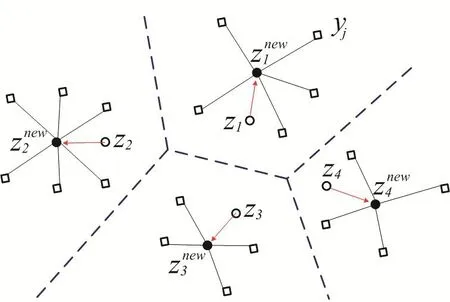
Figure 4:A visual description of probabilistic Lloyd’s method.

A visual description about the probabilistic Llyod’s method is shown in Fig.4.The hollow circles denote the previous positions of the generators and the dashed lines denote the edge of their corresponding Voronoi tessellation.The hollow squares represent the random Monte Carlo sampling points during a single iteration of this algorithm.The solid dark circles denote the average coordinate of random sampling points or the new positions of the kernel points.The red arrows denote path from the previous generators to new generators.Fig.5 shows the centroidal Voronoi tessellation after iterations from the initial 64 Halton sequence points with the density functionρ(X)=1

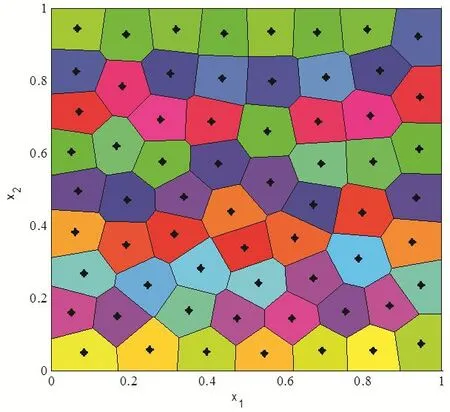
Figure 5:Centroidal Voronoi diagram for a constant density function.

3　Cell characteristics and cell division simulation

3.1　Cell characteristics

A typical cell has a complicated structure in real world[Jones and Chapman(2012);Lodish(2008)].For epithelial cell,it is characterized by a cuboidal cell shape,nuclei localized at the base of the cell,and asymmetrical distribution of proteins at the membrane[Braga(2000)].Generally,cell cycle involves five main states:Resting phase(G0 phase),Increasing phase(G1 phase),Synthetic phase(S phase),Pre-mitotic phase(G2 phase),and Mitotic phase(M phase)[Lipkin et al.(1963)].Cell division models are categorized by two main features of mechanism based on how mother cell separates into daughter cells.The first mechanism involves daughter cells being placed beside the mother cell instantaneously[Bodenstein(1986)].The other mechanism considers actual mitotic steps(including M phase and interphase),and is a more physically realistic model for cell division[Bodenstein and Stern(2005);Gibson et al.(2011)].In fact,in order to simplify the problem,many studies on epithelial cells were based on polygonal shape disregarding the detail feature inside the cells[Aegerter-Wilmsen et al.(2010);Dahmann et al.(2011);Oates et al.(2009)].Therefore,here we also focus on the polyhedral shape modeling without considering the detailed feature inside the cell,such as cell nucleus and cytoplasm.The complicated cell cycle is ignored and we only considered M phase in this study.

3.2　Division procedure

By using the instantaneous cell division mechanism we are able to numerically simulate the evolution of epithelial cell division and cell rearrangements.In order to simulate the development of polygonal cells based on Voronoi tessellation method,the original Voronoi generator is generated by Halton sequence.The prime base onxaxis is 2 and prime base alongyaxis is 3.After several iterations controlled by iteration steps,the polygonal diagram is the centroidal Voronoi cells,see Fig.6(a).We select one cell(the maximum area cell or a random cell),grow the cell volume to almost twice of the normal cell and divide it by the following algorithm:the cell is divided by introducing a new edge that is formed at a specific cleavage angle or a random angle and the new edge passes through the center of Voronoi cell,which will divide the cell into two equal parts,see Fig.6(b).Through this algorithm,the original cell center point is separated into two points and the connection line between these two new points is perpendicular to the new edge.Then,the two daughter cells are relaxed to the new con figuration according to the probabilistic Lloyd’s method,see Fig.6(c).The cell division continues via repeating the above processes

3.3　Simulation results

In cell division simulation,we start with a centroidal Voronoi tessellation of16cells and simulate proliferation by repeating procedures described in Section 3.2.First,four single-cell division cases are considered.Case 1:Maximum area cell is picked as the division cell and the cleavage angle is specified along 45◦or−45◦plane.Case 2:Maximum area cell is selected and the cleavage angle is random.Case 3:The division cell is selected randomly and the cleavage angle is speci fied along 45◦or−45◦plane.Case 4:Both division cell and cleavage angle are random during the division moment.Initially,there are 16 cells in a predetermined lattice model,the dimension of the model is 100µm×100µm.The initial average cell size used in these simulations is around 25µm[De Paiva et al.(2006)].The number of cells is increasing during the division process.And after cell remodeling,the cell topological structures are shown in Figs.7-10.The total cell number increased from 16 to 81 and total cell cluster volume increased from 100µm×100µmto approximately 225µm×225µm.Many morphogenetic processes are accomplished by coordinated cell rearrangements.These rearrangements are accompanied by substantial shifts in the neighbor relationships between cells[Weliky and Oster(1990)].

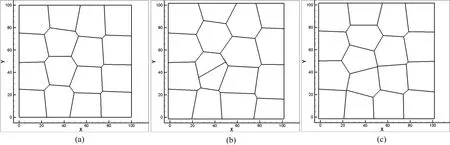
Figure 6:Cell division process in a restricted lattice-based box.

In Fig.11,we plot the cell division number versus division cycle time for the four cases and we notice that the cell division number increases sharply at the initial stage and become slower as cell division proceeds,which implies the division consumption time increases as cycle increases[Lesher et al.(1961)].In fact,if considering the cell apoptosis,the cell division curve will drop down after several hours and the tangent of the curve will be negative.Cells stop dividing or die because the genetic factors are getting lower and lower after each replication.For instance,the telomeres,protective bits of DNA on the end of a chromosome required for replication,get shorten with each copy,eventually being consumed.

In real world,there might be multiple mother cells dividing simultaneously to develop the tissues[Porter et al.(1973)].Fig.12 shows the process of two cells proliferation at the same time.The division procedure is the same as in section 3.2 and the cleavage angle is specified along 45◦and−45◦.The cell topology after rearrangements is shown in Fig.13.In addition,the cell division number versus cycle time for simultaneously double-cell division and single-cell division is plotted in Fig.14.

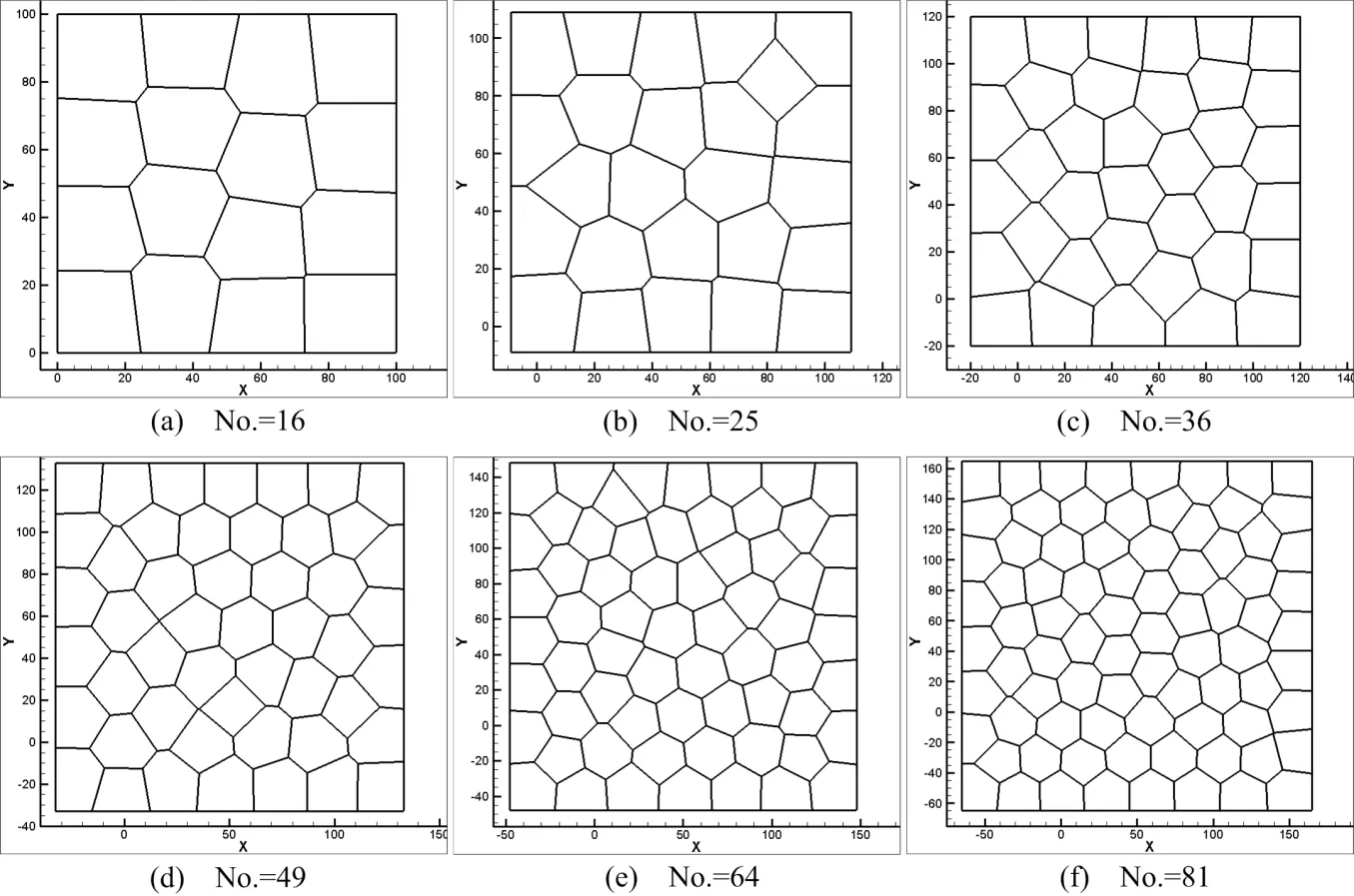
Figure 7:Cell topology and morphology(Case 1).

Figure 8:Cell topology and morphology(Case 2).

Figure 9:Cell topology and morphology(Case 3).

Figure 10:Cell topology and morphology(Case 4).

Figure 11:Reduced division time vs.cell division number.

Figure 12:Doublecell division process.

4　Discussions and conclusions

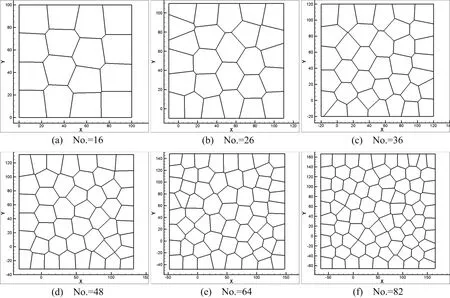
Figure 13:Cell topology and morphology(Double-cell division).

Figure 14:Reduced division time vs.cell division number.

We have developed a numerical simulation tool and used it to simulate cell division.Different cleavage angles are investigated.Actually,the cleavage plane is crucial to numerous processes and may determine the position of the two daughter cells after division[Fernández-Miñán et al.(2007)].Some studies on control of cleavageplane orientation indicated that the consequences of cleavage-plane misorientation can cause polycystic kidney disease and organ malformation to tumorigenesis[Fischer et al.(2006);Gibson et al.(2011);Gong et al.(2004);Quyn et al.(2010);Saburi et al.(2008)].In our simulations(Case 1,Case 2,and Case 4),we show that different cleavage angle results in different cell topological distributions in the same lattice-based model,see Fig.7,Fig.8 and Fig.10.Meanwhile,the position of the daughter cells after division is dependent on the cleavage-plane angle.In return,this might determine the cleavage-plane orientation.Comparing Fig.7 and Fig.9,we can see the position of replicated cells affects the subsequent morphogenic development as well.If the replicated cells are constrained in a small region,this condition may result in cyst.Polycystic kidney disease studies indicate that early cyst formation is associated with an increase in the number of cell in the circumference of dilated tubules[Boletta and Germino(2003);Fischer et al.(2006);Gresh et al.(2004)].Double-cell division simultaneously influences the structure of cell topology,see Fig.9 and Fig.12.Current cell proliferation alters the local cell topology,which is associated with the interplay between cell shape and cleavage-plane orientation.For instance,a pentagon may become a hexagon because of the division of surrounding cells.In turn,this behavior affects the preceding cell division plane angle and polarization.

From the relationship of cell division number and cell division cycle shown in Fig.11 and Fig.14,as cell division proceeds,the division consumption time increases with the increase of cell cycles.The distance between data points also indicates that the cell division time increases as division cycle increases.Besides,the behavior of two mother cells dividing at the same time doesn’t shorten the cycle time by half to reach the same number of new replicated cells.

The limitations of the current study are obvious, first of all,we don’t consider the whole cell cycle during cell replication,such as cell physical growth and apoptosis[Evan and Vousden(2001)].Second,cell division doesn’t involve any external factors or interactions among cells,such as cell deformation[Zeng and Li(2012)]and cell-cell interaction or extracellular matrix effects[Curtis and Seehar(1978);Folkman and Moscona(1978)].Third,the daughter cell is generated instantaneously beside the mother cell,which doesn’t consider the actual mitotic process.The cell division model presented in this work is a primitive one.In our future study,we will consider cell deformation,cell-cell interaction,cell physical growth and apoptosis.The current study provides a numerical tool and may open a door for more realistic and more accurate modeling of cell division,especially for epithelial cells.

Acknowledgement:The research effort is supported by the University of Texas at San Antonio(UTSA)and supported in part by the National Science Foundation(HRD-0932339 through the CREST Center for Simulation,Visualization and Real Time Computing).The computations are performed on computing resources provided by UTSA at the UTSA Data Center.

Reference

Aegerter-Wilmsen,T.;Smith,A.C.;Christen,A.J.;Aegerter,C.M.;Hafen,E.;Basler,K.(2010):Exploring the effects of mechanical feedback on epithelial topology.Development,vol.137,no.3,pp.499-506.

Alberts,B.(2008):Molecular biology of the cell.Garland Science.

Baena-López,L.A.;Baonza,A.;García-Bellido,A.(2005):The Orientation of Cell Divisions Determines the Shape of Drosophila Organs.Current Biology,vol.15,no.18,pp.1640-1644.

Bhat,C.R.(2003):Simulation estimation of mixed discrete choice models using randomized and scrambled Halton sequences.Transportation Research Part B:Methodological,vol.37,no.9,pp.837-855.

Bodenstein,L.(1986):A dynamic simulation model of tissue growth and cell patterning.Cell Differentiation,vol.19,no.1,pp.19-33.

Bodenstein,L.;Stern,C.(2005):Formation of the chick primitive streak as studied in computer simulations.Journal of Theoretical Biology,vol.233,no.2,pp.253-269.

Boletta,A.;Germino,G.G.(2003):Role of polycystins in renal tubulogenesis.Trends in cell biology,vol.13,no.9,pp.484-492.

Braga,V.(2000):Epithelial cell shape:cadherins and small GTPases.Experimental cell research,vol.261,no.1,pp.83-90.

Brodland,G.W.;Viens,D.;Veldhuis,J.H.(2007):A new cell-based FE model for the mechanics of embryonic epithelia.Computer methods in biomechanics and biomedical engineering,vol.10,no.2,pp.121-128.

Chi,H.;Mascagni,M.;Warnock,T.(2005):On the optimal Halton sequence.Mathematics and Computers in Simulation,vol.70,no.1,pp.9-21.

Cowin,S.C.;Doty,S.B.(2007):Tissue mechanics.Springer.

Curtis,A.;Seehar,G.(1978):The control of cell division by tension or diffusion.Dahmann,C.;Oates,A.C.;Brand,M.(2011):Boundary formation and maintenance in tissue development.Nature Reviews Genetics,vol.12,no.1,pp.43-55.

Dallon,J.C.;Othmer,H.G.(2004):How cellular movement determines the collective force generated by the Dictyostelium discoideum slug.Journal of Theoretical Biology,vol.231,no.2,pp.203-222.

De Paiva,C.S.;P flugfelder,S.C.;Li,D.Q.(2006):Cell size correlates with phenotype and proliferative capacity in human corneal epithelial cells.Stem Cells,vol.24,no.2,pp.368-375.

Du,Q.;Faber,V.;Gunzburger,M.(1999):Centroidal Voronoi tessellations:Ap-plications and algorithms.SIAM Review,vol.41,no.4,pp.637-676.

Dubertret,B.;Rivier,N.(2000):Geometrical models of the renewal of the epidermis.Comptes Rendus de l’Académie des Sciences-Series III-Sciences de la Vie,vol.323,no.1,pp.49-56.

Evan,G.I.;Vousden,K.H.(2001):Proliferation,cell cycle and apoptosis in cancer.Nature,vol.411,no.6835,pp.342-348.

Farhadifar,R.;Röper,J.-C.;Aigouy,B.;Eaton,S.;Jülicher,F.(2007):The influence of cell mechanics,cell-cell interactions,and proliferation on epithelial packing.Current Biology,vol.17,no.24,pp.2095-2104.

Fernández-Miñán,A.;Martín-Bermudo,M.D.;González-Reyes,A.(2007):Integrin Signaling Regulates Spindle Orientation in Drosophila to Preserve the Follicular-Epithelium Monolayer.Current Biology,vol.17,no 8,pp.683-688.

Fischer,E.;Legue,E.;Doyen,A.;Nato,F.;Nicolas,J.-F.;Torres,V.;Yaniv,M.;Pontoglio,M.(2006):Defective planar cell polarity in polycystic kidney disease.Nature genetics,vol.38,no.1,pp.21-23.

Folkman,J.;Moscona,A.(1978):Role of cell shape in growth control.

Garikipati,K.;Arruda,E.;Grosh,K.;Narayanan,H.;Calve,S.(2004):A continuum treatment of growth in biological tissue:the coupling of mass transport and mechanics.J.Mech.Phys.Solids,vol.52,no.7,pp.1595-1625.

Gibson,M.C.;Patel,A.B.;Nagpal,R.;Perrimon,N.(2006):The emergence of geometric order in proliferating metazoan epithelia.Nature,vol.442,no.7106,pp.1038-1041.

Gibson,W.T.;Gibson,M.C.(2009):Cell topology,geometry,and morphogenesis in proliferating epithelia.Current topics in developmental biology,vol.89,pp.87-114.

Gibson,W.T.;Veldhuis,J.H.;Rubinstein,B.;Cartwright,H.N.;Perrimon,N.;Brodland,G.W.;Nagpal,R.;Gibson,M.C.(2011):Control of the mitotic cleavage plane by local epithelial topology.Cell,vol.144,no.3,pp.427-438.

Gong,Y.;Mo,C.;Fraser,S.E.(2004):Planar cell polarity signalling controls cell division orientation during zebra fish gastrulation.Nature,vol.430,no.7000,pp.689-693.

Gresh,L.;Fischer,E.;Reimann,A.;Tanguy,M.;Garbay,S.;Shao,X.;Hiesberger,T.;Fiette,L.;Igarashi,P.;Yaniv,M.(2004):A transcriptional network in polycystic kidney disease.The EMBO Journal,vol.23,no.7,pp.1657-1668.

Halton,J.H.(1960):On the ef ficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals.Numerische Mathematik,vol.2,no.1,pp.84-90.

Hess,S.;Polak,J.(2003):An alternative method to the scrambled Halton sequence for removing correlation between standard Halton sequences in high dimensions.ERSA conference papers.

Hildebrand,J.D.(2005):Shroom regulates epithelial cell shape via the apical positioning of an actomyosin network.Journal of cell science,vol.118,no.22,pp.5191-5203.

Honda,H.(1978):Description of cellular patterns by Dirichlet domains:The two dimensional case.Journal of Theoretical Biology,vol.72,no.3,pp.523-543.

Honda,H.;Tanemura,M.;Yoshida,A.(2000):Differentiation of wing epidermal scale cells in a butter fl y under the lateral inhibition model-appearance of large cells in a polygonal pattern.Acta biotheoretica,vol.48,no.2,pp.121-136.

Jayabal,K.;Menzel,A.(2011):Application of polygonal finite elements to two dimensional mechanical and electro-mechanically coupled problems.Computer Modeling in Engineering&Sciences(CMES),vol.73,no.2,pp.183-207.

Jones,G.W.;Chapman,S.J.(2012):Modeling growth in biological materials.SIAM Review,vol.54,no.1,pp.52-118.

Ju,L.;Du,Q.;Gunzburger,M.(2002):Probabilistic methods for centroidal Voronoi tessellations and their parallel implementations.Parallel Computing,vol.28,no.10,pp.1477-1500.

Lecuit,T.;Lenne,P.F.(2007):Cell surface mechanics and the control of cell shape,tissue patterns and morphogenesis.Nature Reviews Molecular Cell Biology,vol.8,no.8,pp.633-644.

Lesher,S.;Fry,R.J.M.;Kohn,H.I.(1961):Age and the generation time of the mouse duodenal epithelial cell.Experimental cell research,vol.24,no.2,pp.334-343.

Linde,Y.;Buzo,A.;Gray,R.(1980):An algorithm for vector quantizer design.Communications,IEEE Transactions on,vol.28,no.1,pp.84-95.

Lipkin,M.;Bell,B.;Sherlock,P.(1963):Cell proliferation kinetics in the gastrointestinal tract of man.I.Cell renewal in colon and rectum.Journal of Clinical Investigation,vol.42,no.6,pp.767.

Lloyd,S.(1982):Least squares quantization in PCM.Information Theory,IEEE Transactions on,vol.28,no.2,pp.129-137.

Lodish,H.(2008):Molecular cell biology.Macmillan.

MacQueen,J.(1967):Some methods for classification and analysis of multivariate observations.Proceedings of the fifth Berkeley symposium on mathematical statistics and probability,vol.1,pp.281-297.

Meineke,F.;Potten,C.S.;Loeffler,M.(2001):Cell migration and organization in the intestinal crypt using a lattice-free model.Cell proliferation,vol.34,no.4,pp.253-266.

Oates,A.C.;Gorfinkiel,N.;González-Gaitán,M.;Heisenberg,C.-P.(2009):Quantitative approaches in developmental biology.Nature Reviews Genetics,vol.10,no.8,pp.517-530.

Porter,K.;Prescott,D.;Frye,J.(1973):Changes in surface morphology of Chinese hamster ovary cells during the cell cycle.The Journal of cell biology,vol.57,no.3,pp.815-836.

Quyn,A.J.;Appleton,P.L.;Carey,F.A.;Steele,R.J.;Barker,N.;Clevers,H.;Ridgway,R.A.;Sansom,O.J.;Näthke,I.S.(2010):Spindle orientation bias in gut epithelial stem cell compartments is lost in precancerous tissue.Cell stem cell,vol.6,no.2,pp.175-181.

Resino,J.;Salama-Cohen,P.;García-Bellido,A.(2002):Determining the role of patterned cell proliferation in the shape and size of the Drosophila wing.Proceedings of the National Academy of Sciences,vol.99,no.11,pp.7502-7507.

Saburi,S.;Hester,I.;Fischer,E.;Pontoglio,M.;Eremina,V.;Gessler,M.;Quaggin,S.E.;Harrison,R.;Mount,R.;McNeill,H.(2008):Loss of Fat4 disrupts PCP signaling and oriented cell division and leads to cystic kidney disease.Nature genetics,vol.40,no.8,pp.1010-1015.

Schaller,G.;Meyer-Hermann,M.(2005):Multicellular tumor spheroid in an offlattice Voronoi-Delaunay cell model.Physical Review E,vol.71,no.5,051910.

Taber,L.A.(1995):Biomechanics of growth,remodeling,and morphogenesis.Applied mechanics reviews,vol.48,no.8,pp.487-545.

Théry,M.;Bornens,M.(2006):Cell shape and cell division.Current opinion in cell biology,vol.18,no.6,pp.648-657.

Tomasek,J.J.;Gabbiani,G.;Hinz,B.;Chaponnier,C.;Brown,R.A.(2002):Myo fibroblasts and mechano-regulation of connective tissue remodelling.Nature Reviews Molecular Cell Biology,vol.3,no.5,pp.349-363.

Weliky,M.;Minsuk,S.;Keller,R.;Oster,G.(1991):Notochord morphogenesis in Xenopus laevis:simulation of cell behavior underlying tissue convergence and extension.Development,vol.113,no.4,pp.1231-1244.

Weliky,M.;Oster,G.(1990):The mechanical basis of cell rearrangement.Development,vol.109,no.2,pp.373-386.

Zeng,X.;Li,S.(2012):A three dimensional soft matter cell model for mechanotransduction.Soft Matter,vol.8,no.21,pp.5765-5776.