Design Evaluation of a Particle Bombardment System Used to Deliver Substances into Cells

Eduardo M.B.Campelloand Tarek I.Zohdi

1　Introduction

Modern cell biology makes extensive use of delivery mechanisms to deliver foreign substances into cells.Proteins,drugs,genetic material,biological stains,and many other materials are often desired to be transported to the interior of cells to undertake a speci fic task.The cell membrane(in case of plant cells,also the cell wall)constitutes the main physical barrier in this regard.Among the existing technologies to accomplish such transport,particle bombardment guns have been preferred in recent years in many applications.This is partly due to their ability to deal with cells bothin vitroandin vivo(i.e.,cells either in suspension or in their natural environment)and with groups of cells simultaneously(instead of only single cells at a time).Particle guns consist of a channeled accelerator that shoots single particles or streams of particles of a noble,inert material(usually gold or tungsten)to which the desired foreign substances are attached.They were first introduced by Sanford and coworkers in the late 1980s(see the seminal papers[Sanford,Klein,Wolf and Allen(1987)]and[Klein,Wolf,Wu and Sanford(1987)]),and rely on a very simple principle:if the incoming particles have the appropriate sizes and are accelerated to the appropriate velocities,they should readily penetrate thin barriers such as cell walls and cell membranes,thereby entering the cell cytoplasm.The idea is schematically illustrated in Fig.1,where typical dimensions are also shown.

In the design of particle guns,the lipid bilayer structure of the cell membrane is a primary aspect to be considered.Lipid molecules can be idealized as a spherical polar head(representing a phosphoric group)that has one or two elongated tails(representing hydrocarbon,fatty acid chains).In aqueous media,they organize themselves into various types of structures due to their amphiphilic properties(the polar heads are hydrophilic,the hydrocarbon chains are hydrophobic),one of which is the two-layer formation that is observed in cellular membranes.The forces that hold them together in such arrangement are not due to strong covalent or ionic bonds,but instead arise from weaker van der Waals,hydrophobic and hydrogen-bonding interactions.This aspect provides the membrane a very soft,flexible,almost fluid-like behavior,and yet good response to both stretching and bending deformations are observed(along with excellent selective permeability).The transport of substances across the membrane barrier by means of particle bombardment guns is greatly governed by the mechanical characteristics of this structure.

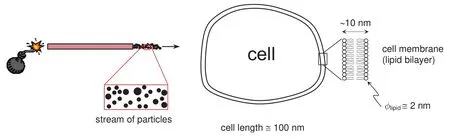
Figure 1:Schematic of a particle bombardment gun for the delivery of substances into a cell.

This work deals with the computational modeling of particle bombardment guns and aims at establishing a basic framework for design evaluation of these types of delivery mechanisms.We use a particle-based(discrete element method)model recently proposed by the authors in[Campello and Zohdi(2014)]to describe both the incoming stream of particles and the cell membrane,and perform parametric simulations of the system by making the stream’s mean particle size,velocity and aspect ratio as design parameters.More specifically,these parameters are treated as random variables whose values are sampled from underlying probability distribution functions,with which we construct several sets of design vectors.Each design vector generates a computational particle problem that is then solved numerically with our particle solver.In this latter,the compliance of the cell is taken into account by using an appropriate(yet simple)model of the lipid’s bonding interactions,together with consideration of the cell internal pressure.Both the bonding and internal pres-sure parameters are assumed to be known and held with fixed values on all analyses.Two measures(or indicators of performance)are defined to quantify respectively the delivery success and the membrane damage associated with each design vector or simulation.After performing all simulations,we compute the mean value,standard deviation and coefficients of variation of the design parameters and of the two defined measures.We also compute the correlation coefficients of the two measures with respect to each of the design parameters.These statistics allow us to make interpretations such as how variabilities in the input parameters propagate to the output results,and what are the best combinations of parameter values that lead to(i)the highest amount of particle delivery and(ii)the lowest level of membrane damage.Other basic trends in the system can also be identified.

It is evident that there are multiple parameters that govern the response of cells against the impact by a stream of particles.Yet,with the aim of solely establishing a framework for rapid parametric investigations for design evaluation,and of showing how the synergy of parameters can be identified,here we work only with the three parameters stated above.We must mention,moreover,that there exists a number of other theoretical and/or computational approaches that could be used to study the transport of substances across the cell membrane,such as stochastic dynamics[Wang,Sigurdsson,Brandt and Atzberger(2013);Pastor and Venable(1993)],Monte Carlo simulations[Hac,Seeger,Fidorra and Heimburg(2005);Pastor(1994)],molecular dynamics models[Tieleman,Marrink and Berendsen(1997);Delemotte and Tarek(2012);Andoh,Okazaki and Ueoka(2013)],mean field models[Khelashvili,Weinstein and Harries(2008)],continuum mechanics models with spatial discretizations[Rangamani,Agrawal,Mandadapu,Oster and Steigmann(2013)],etc.,to name just a few.Yet,at the tens of nano-to a few microtime and length scales,we believe that particle-based models are the most suited when one is interested in the overall,collective behavior of the system.They allow for simpler representations of the whole cell and incoming substances(with no need for detailed descriptions of the complex short-range forces that act between the polar headgroups and hydrocarbon chains of the lipid molecules).Also,multiple contact/impact with the opening of localized holes on the membrane(localized“rupture”)is straightforward to characterize.They allow for the construction of rapid simulation tools.With such tools,particle bombardment guns can be more thoroughly designed and tested without the need to resort to a great number of physical experiments.Physical experiments can be expensive and time consuming when dealing with cells,and the number of parameters that can be adjusted within feasible cost and time is very limited when compared to computational investigations.For details on particle methods,see e.g.[Bicanic(2004);Pöschel and Schwager(2004);Duran(1997)].

The paper is organized as follows:in Section 2 we present an overview of the equations that govern the dynamics of particle systems,with emphasis on the several types of mechanical forces involved herein and their representations;in Section 3 we present a brief description of the particle model adopted here for the cell membrane,which is taken from[Campello and Zohdi(2014)];in Section 4 we give an outline of our numerical solution scheme to the system’s equations;in Section 5 we show how we construct the design vectors and the associated particle problems,perform the corresponding numerical simulations,and extract the simulations’results and statistics;and in Section 6 we derive our conclusions.

Throughout the text,plain italic lettersdenote scalar quantities,whereas boldface italic onesdenote vectors in a three-dimensional Euclidean space.The inner product of two vectors is denoted by

whereuiandvi(i=1,2,3)are the corresponding three components of the vectors,and the norm of a vector by

2　Dynamics of Particle Systems

The primary assumption in the computational model that we use is that both the incoming substances and the lipid molecules of the cell membrane are a collection of spherical particles forming a discrete dynamical system.A purely mechanistic(Newtonian)description is then followed(biological and chemical effects are not considered).The particles are assumed to be small enough so that the effect of their rotations with respect to their center of mass is unimportant to their overall motion.Permanent deformations due to contact and collisions are supposed to be minor and thereby ignored,which means that all particles remain spherical and with constant radius throughout.Effects of temperature changes are also considered to be irrelevant–although these can be easily incorporated,following e.g.the scheme proposed in[Zohdi(2012)].

Let the system be comprised ofNpparticles,each one with known massmiand known radiusand let us denote the position vector of a particle bythe velocity vector byand the acceleration vector byAccording to Newton’s second law,at every time instanttthe following equation must hold for each particle:

wherecenvis a damping parameter andis the(local)velocity of the surrounding fluid.One should notice that this scheme constitutes a one-way-only kind of coupling between the fluid and the particle,in the sense that the fluid affects the particle but the particle does not affect the fluid(more elaborate,fully coupled models can be constructed if necessary,although this increases drastically the complexity of the solution scheme,since the fluid local velocity and pressure fields need to be introduced as additional variables).Other environmental forces could be considered in(5),such as electric forces due to external electric fields,magnetic forces due to external magnetic fields,etc.,but these are not considered in the present work.

The forces due to bonding or adhesive interactions with other particles are given by

whereNbis the number of particles that are bonded to particleiandis the(binary)bonding force that acts between particleiand particlej.This force has the general expression

in whichis a parameter dictating the intensity of the bonding for the pairandis the unit vector that points from the center of particleito the center of particlej,i.e.,

Vectorwill be from now on referred to as the pair’s central direction.Scalarcan be modeled in a number of ways,such as by using a combination of attractive and repulsive force coefficients that are functions of the distance between the particles[Zohdi(2012)](this can be understood as derived from a generalized Mie’s potential,of which the classical Lennard-Jones potential[Lennard-Jones(1924)]is a special case),by using surface energy arguments[Johnson,Kendall and Roberts(1971);Israelachvili(2011)],direct van de Waals effects,etc.In Section 3 we show the model that we adopt for the purpose of this work,which was introduced by the authors in[Campello and Zohdi(2014)](see also[Campello(2014)])and is based on the presence of a fictitious spring-dashpot device connecting particlesiandj.The forces due to contact and collisions with other particles are modeled here with an overlap-based scheme.Accordingly,the contact force is assumed to be a function of the amount of geometrical overlap or penetration(i.e.,“deformation”)between the particles in contact.We follow Hertz’s elastic contact theory(see e.g.[Johnson(1985)])and adopt the following expression for

whereNcis the number of particles that are in contact with particlei,is the(binary)contact force that acts between the contacting pair

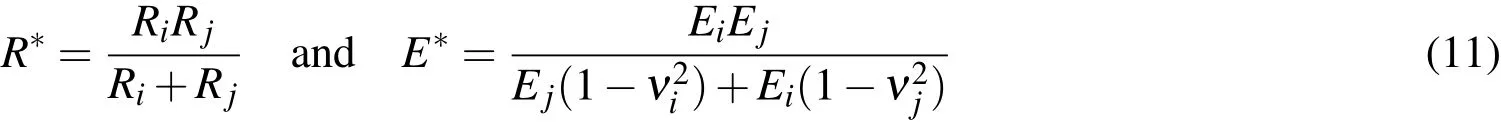
are the effective radius and the effective elasticity modulus of the contacting pair(in whichEi,Ejandνi,νjare the elasticity modulus and the Poisson coefficient of particlesiandj,respectively),

is the geometric overlap(or penetration)between the pair in the pair’s central direction,˙δis the rate of this penetration(the superposed dot denotes differentiation with respect to time),anddis a damping constant that is introduced to allow for some energy dissipation.Fig.2(top part)provides a schematic illustration of the contact/collision for a colliding pair.

Figure 2:Contact/collision between two particles.

The damping constantdis taken here following the ideas of[Wellmann and Wriggers(2012)],which means

whereinξis the damping rate of the collision(which must be specified)andm∗is the effective mass of the colliding pair,i.e.,

The damping rateξenables us to enforce the type of energy dissipation that shall occur during the collision in the pair’s central direction.If the colliding pair is seen as a one-dimensional spring-dashpot system(SDS)of massm∗and damping rateξ,its dynamics can be fully controlled by specifying appropriateξ’s.Recalling the solution to a vibration problem of a 1-D SDS,it follows that:(1)whenξ=0,no damping exists and the collision is a perfectly elastic,energy-conserving one(undamped SDS);(2)when 0<ξ<1,small to moderate damping exists and energy dissipation occurs at small to moderate rates(underdamped SDS);(3)whenξ=1,strong damping exists and rapid energy dissipation is observed(critically damped SDS);and(4)whenξ>1,very strong damping with rapid dissipation is observed(overdamped SDS).Equation(13)is a generalization of the ideas proposed by Cundall and Strack in their seminal work[Cundall and Strack(1979)],wherein only critically damped collisions were considered.

The forces due to friction,which arise from the contacts/collisions,are modeled by assuming that the friction coefficients of all colliding pairs are small enough so that a continuous slide(with an opposing dynamic friction force)is to be expected during the entire duration of the contact/collision(see Fig.2,bottom part).By“continuous slide”we mean that there is to be no stick between the contacting pair.Although a stick-slip model could be considered,we find it to be unnecessary for the problem that we are concerned with in this work.Thereby,here we write is the tangential direction of the contact/collision,which is the direction of the tangential relative velocity ofiandj,in which

3　Particle Model for the Cell Membrane

We follow the membrane model that has been proposed by the authors in[Campello and Zohdi(2014)]and adopt a two-dimensional,circular-shaped idealization of the cell,as depicted in Fig.3(a fully three-dimensional one can be considered without any modification,at the only expense of having more particles in the system).For simplicity,the presence of other substances on the membrane surface rather than lipids(proteins,sugars,cholesterols,etc.)is ignored.Within this setting,each lipid molecule is represented by a spherical particle(corresponding to the molecule’s headgroup)that is bonded to its neighboring ones of the same layer by means of spring-dashpots(SDs),as indicated in the upper zoom of Fig.3.To capture the“through-the-thickness”or“transverse”bonding that maintains the two layers together(which is in great part due to hydrophilic/hydrophobic interactions with the surrounding aqueous media),transversal SDs are placed connecting particles in the cell’s radial direction.And to account for circumferential interactions between the two layers,crosswise SDs are introduced.The scheme is as depicted in the lower zoom of Fig.3,where the dashpots are not shown for the sake of clarity.Each SD has stiffnesskij,damping constantcijand initial lengthL0ij.

Accordingly,on each particleiof the membrane there act five bonding forces,corresponding to the five SDs that are connected toi.This allows us to write,for each of these particles:

are the central components of the particles’velocities.To allow for the bonds to break(rupture)if the particles are pulled apart strongly enough,each SD is provided with a critical strainwhich leads to a critical elongationOnce this critical value is reached,the corresponding SD is turned off,that is,it does not enter the summation in equation(18).

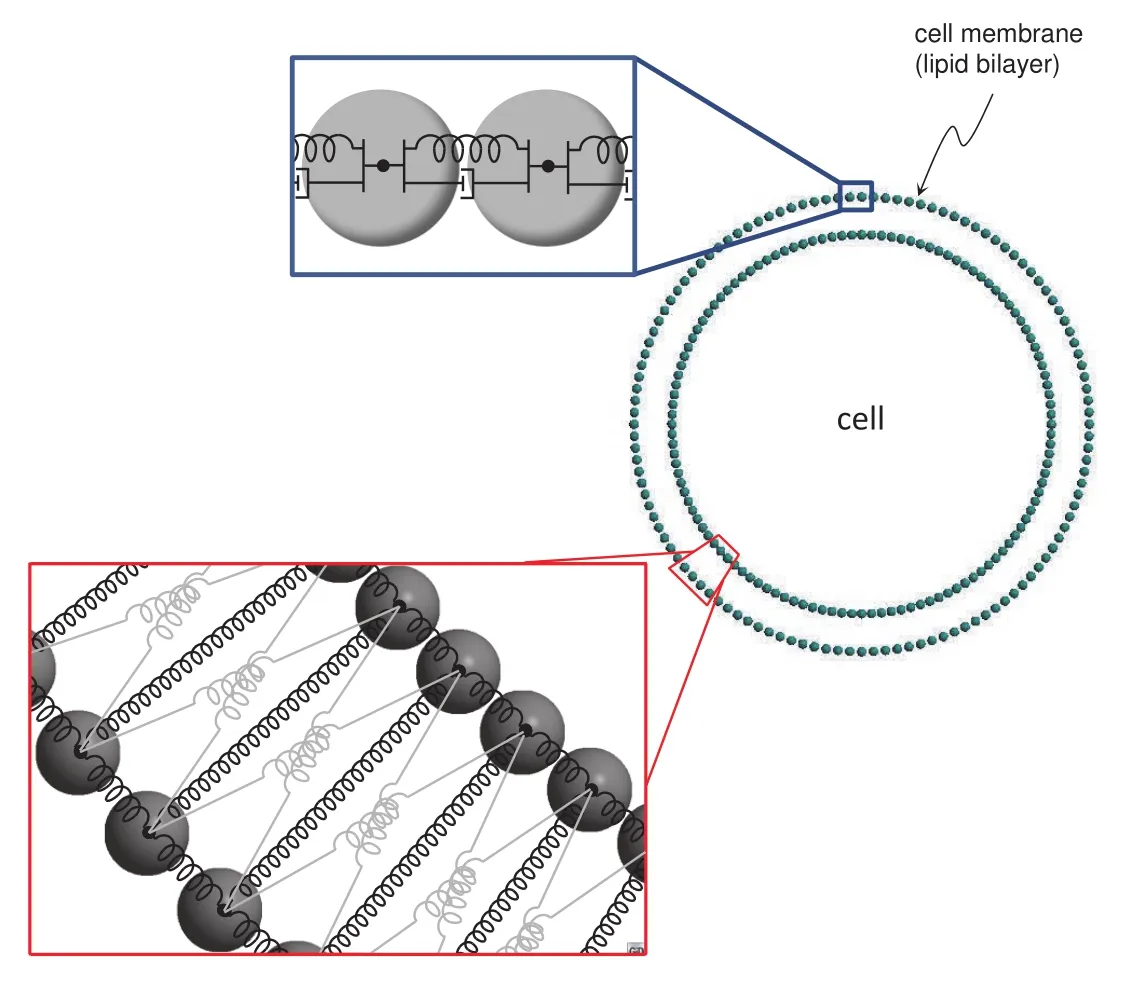
Figure 3:2D representation of the cell membrane and bonding between lipid particles.

The cell compliance or response to mechanical loads is governed not only by this arrangement of SDs but also by the presence of an internal pressure.We consider here that there exists a positive pressure gradient from the interior to the exterior of the cell,which leads to an outward pressure force

on each of the membrane’s inner layer particles.In this case,is the intensity of the pressure force(which is to be specified)andis the local normal direction of the membrane surface at the inner particlei,pointing outwards.Directionis computed for each inner particle by taking successive cross-products involving the particle’s position vectorand its immediate neighboring onesandof the inner layer,and then normalizing the result.One should notice that,since pressure forces are live loads(in the sense that they change their local direction as the membrane deforms),eachhas to be recomputed at every time instant.The intensity,however,is kept here as constant for the sake of simplicity.

One important aspect in this membrane model is how to come up with appropriate values for the springs’stiffnesses.As proposed in[Campello and Zohdi(2014)],here we estimate their values from surface tension arguments,since the value of the surface tension(or interfacial free energy per unit area)for hydrocarbon-water interfaces is well documented in the literature.This is reported as being around 50 mJ/m2for monolayers(although the presence of the hydrophilic headgroup may reduce it to something closer to 20 mJ/m2,see e.g.[Israelachvili(2011)]),so that for bilayers it must be multiplied by two.We check the obtained value against the one that follows from the(more or less known)maximum internal pressure that the cell can undergo before membrane rupture.From static equilibrium arguments on one isolated particle,one can equate the force due to this internal pressure to the resultant(in the radial direction)of the forces of the springs that are connected to the particle.By assuming that all springs have the same stiffness,kijfollows.

The reader should notice in this model that,since each lipid bonding is assumed to behave according to a one-dimensional constitutive relation,more complex laws such as nonlinear hyperelasticity with progressive damage and rupture(allowing for non-abrupt breaking of the bonds)can be straightforwardly considered.

Remark 1.It is important to notice the role of the crosswise SDs.They can be understood as arising from the small lateral interactions that exist between the hydrocarbon chains of adjacent lipid molecules.Their presence is crucial in providing a combined bending behavior for the two layers.Not having them causes each layer to deform as independent sheets upon bending,which is not a realistic behavior.

Remark 2.For a pair of bonded(neighboring)lipid molecules,the spring stiffnesskijand the dashpot constantcijcan be understood as “homogenized”properties that represent the overall(average)behavior of the intermolecular interactions between the two molecules.In fact,we believe that many of the physical properties of the cell membrane can be qualitatively described without the need to resort to detailed representations of the complex short-range forces that act between the polar headgroups and hydrocarbon chains of its lipid molecules.In an analogy with gas-liquid phase interactions in thermodynamics,for example,the classical van der Waals equation of state contains no information on the characteristics and range of intermolecular forces,and yet renders a very satisfactory representation of the phase behavior.

4　Time Integration Scheme for Solution of the System’s Dynamics

For the solution of the system’s dynamics,we start by considering the acceleration vectorof each particle,which may be computed from equation(3).By definition,this vector also follows from the time-continuous differential equation

Integration of(22)between time instantstandt+∆t,together with(3),furnishes

The integral on the right-hand side of(23)is difficult(if not impossible)to be evaluated analytically because of the intricate dependence ofwith time.A numerical approximation is thus necessary and here we adopt the following scheme,which corresponds to the use of a generalized trapezoidal rule:

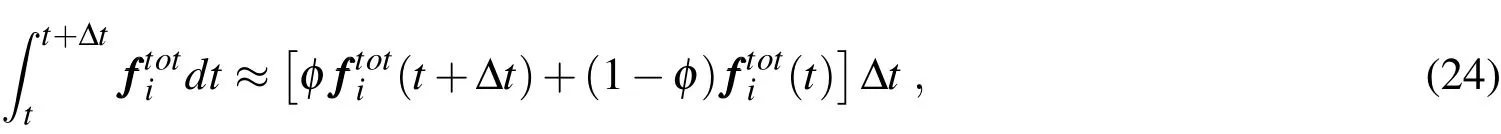
with 0≤ϕ≤1.Ifφ=0,the integration corresponds to an(explicit)forward Euler scheme;ifφ=1,to an(implicit)backward Euler one;and ifφ=0.5,to the(implicit)classical trapezoidal rule.By inserting(24)into(23),one has

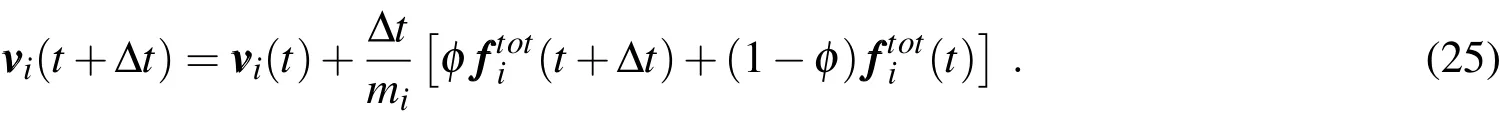
On the other hand,by definition the velocity vectorof each particle is related to the particle’s position by the time-continuous differential equation

This equation can also be integrated betweentandt+∆t,yielding

The integral in(27)is also difficult to be evaluated analytically,and then we adopt the following approximation,similarly to what was done in(24):

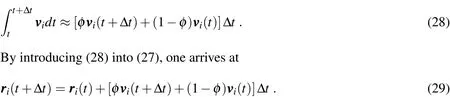
Expressions(25)and(29)constitute a set of equations fori=1,...,Npparticles,with which the velocity and position vectors of each particle att+∆tmay be computed onceare known.This computation,however,cannot be performed directly,since(25)requires the evaluation ofwhich is in turn a function of all unknown position and velocity vectors

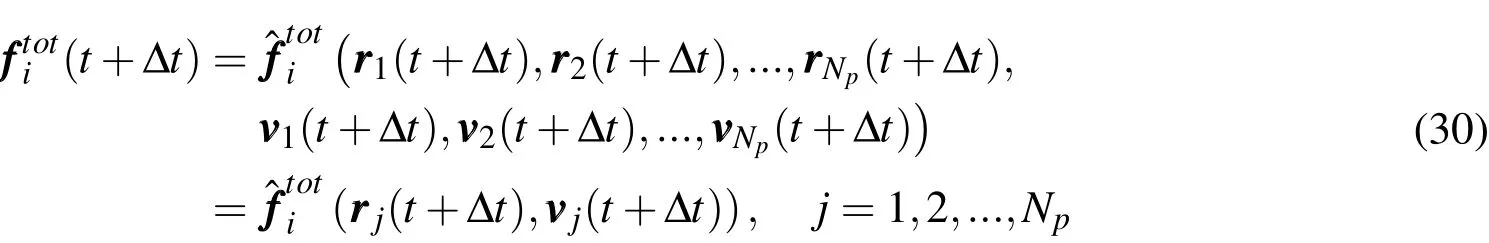
(the notation with a superposed hat introduced above indicates that the quantity is a function of the arguments inside the parentheses).This fact means that all equations are strongly coupled,and a recursive solution is thereby necessary.We adopt here a fixed-point iterative scheme,whose main steps are as summarized in(31).The scheme is relatively easy to be implemented and it is noteworthy that no system matrix is required.Also,adaptivity of the time step size can be straightforwardly incorporated.

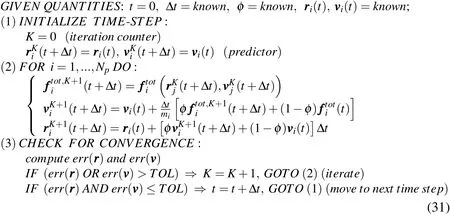
Remark 3.According to(31),one may think that velocities and positions are to be fully updated only after one complete iteration.This would correspond to a Jacobi-type of scheme and is presented like so in(31)only for the sake of algebraic simplicity.What we actually do in step(2)of the algorithm is:for each particlei,we computeusing the velocities and positions of the previous particles that have just been updated within the current iteration,that is,usingandthe values of the previous iteration,are used.This resembles a Gauss-Seidel scheme,which(as it is well known)converges at a faster rate than the Jacobi method,if the Jacobi method converges,or diverges at a faster rate,if the Jacobi method diverges.For details on this subject,the reader is referred to[Axelsson(1994)].

Remark 4.The two error measures in step(3)of(31)are taken as normalized(nondimensional)measures,and are given respectively by

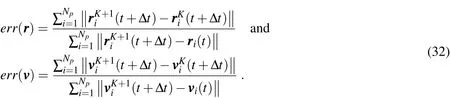
5　Parametric Numerical Simulations

To perform the parametric simulations we are concerned with in this work,we devise the model problem that is depicted in Fig.4.Accordingly,we consider the bombardment of a prokaryotic cell of an ideally circular shape.The cell has external radiusRcell=60 nm,membrane thickness of 10 nm and its lipid molecules have diameterφlipid=2.5 nm.The stream is consisted of particles that occupy a rectangular region of lengthLand widthw,the area of which is constrained to be 15%of the cell area(we say “area”but in a broader sense what we want to constrain is the stream’s volume).Such a constraint is adopted to prevent large volumes of particles from being delivered to the interior of the cell,which could cause excessive swelling and eventually cell rupture.The stream particles are consisted of a polymeric material and their diameters follow a Gaussian distribution of meanφmeanand standard deviationσφ=0.1φmean.Their travelling velocity when leaving the tip of the gun isv.In our computational model,these particles are randomly placed within the regionL×wby means of a standard random sequence addition algorithm,with a packing ratio of 50%(for details on this and other types of particle packing algorithms,the interested reader is referred to[Zhang and Torquato(2013)],and references therein).

For the analysis of different scenarios of delivery success and membrane damage upon bombardment of the cell,we consider the design parameters of the delivery system to beφmean,vandw(withLbeing constrained byThis leads to a parameter space that can be represented by a design vectorΛas indicated below:

The indicators of performance for each design vector(i.e.measures that indicate whether a designΛperforms favorably or unfavorably)are taken as the delivery ratioDRand the membrane damageDAM.We define these two measures respectively by

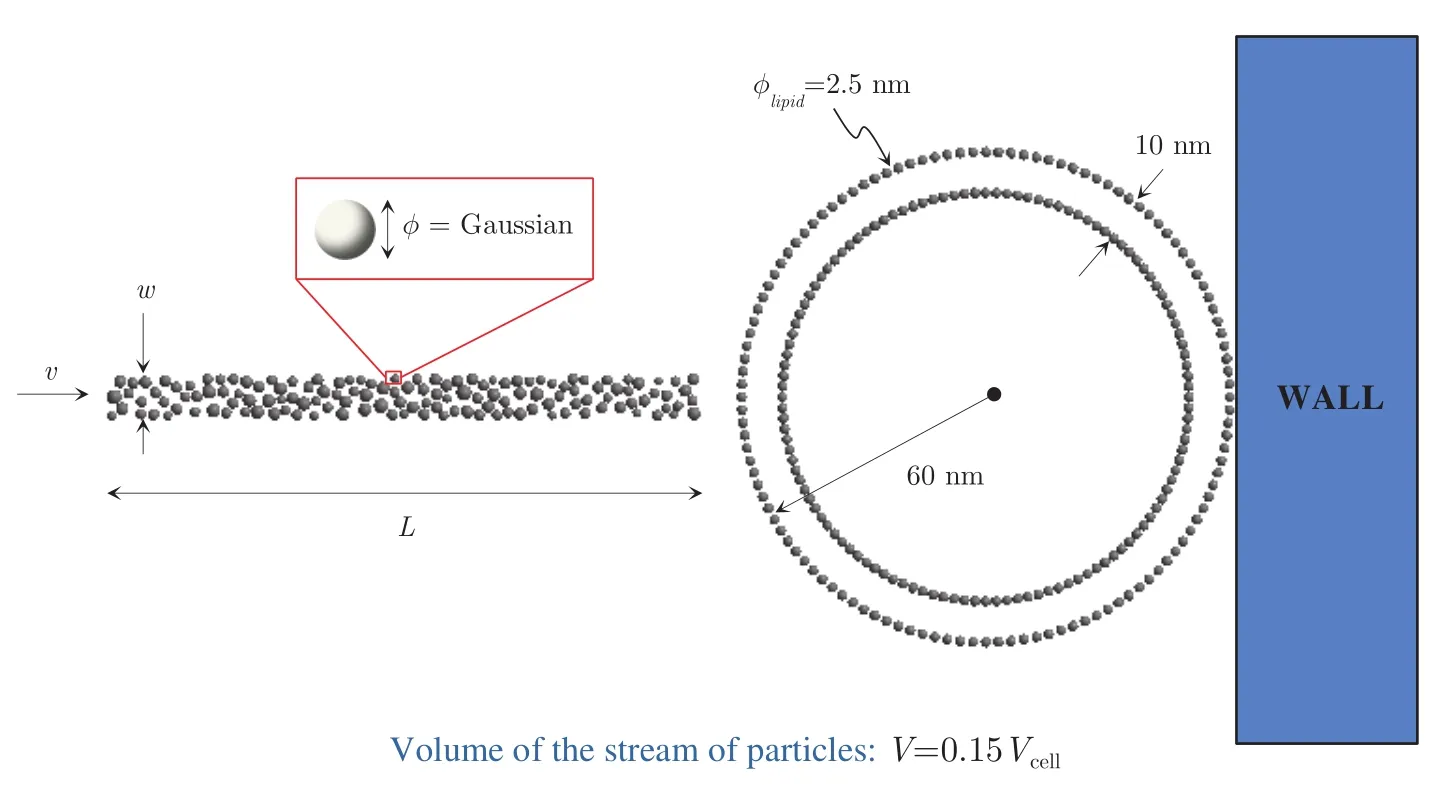
Figure 4:Model problem.

whereNbrokenis the number of broken lipid bonds at the end of a simulation,is the length(or separation)of the broken bondiat the end of the simulation,andis the initial length of the broken bondi.Such a damage measure allows us to quantify the “cumulative strain”of the broken bonds,which can be understood as an indicator of the “total relative size”of the permanent holes that are opened on the membrane due to impact by the stream.Another quantity of interest would be the ratiowhich provides the average strain of the broken bonds or the strain per broken bond.Notice that the value ofNbrokenis not a good measure of damage,since it does not provide information on the extent of the open holes.We generateMsets ofNdesign vectors by sampling values of the design parameters from underlying uniform probability distribution functions.Each design pa-rameter is constrained to fall within the following intervals:

It is assumed that the samples are statistically independent,although they need not be identically distributed.For each design vector,a computational particle problem is generated and resolved.In each of these problems,as mentioned above,the particles of the stream are created by random sequence addition with a packing ratio of 50%.

Once all problems are resolved,the obtained values ofDRandDAMare processed to obtain their mean valueµ,standard deviationσ,coefficient of variationCOV(the ratio of mean to standard deviation)and correlation coefficientsCOR(with respect to each of the design parameters)within each set.These allow us to identify basic trends of the system.The coefficients of variation,for example,are non-dimensional measures of dispersion of the obtainedDRandDAM,and provide a zero-order estimate of the extent to which the variabilities in the input parameters propagate to the output results.The correlation coefficients,in their turn,are first-order estimates of the strength and direction of the relation between any two parameters(one input and one output).If the greatest values of the input parameter mostly correspond to the greatest values of the output parameter,and the same holds for the smallest values,i.e.,if the parameters tend to show similar behavior,the correlation coefficient between these two parameters is positive.In the opposite case,it is negative.The higher the value ofCOR,the stronger is the linear relation between the two parameters.The overall framework for the parametric simulations is as summarized in Algorithm 1(this framework is based on the scheme proposed by[Mukherjee and Zohdi(2014)]for the design evaluation of porous material layers).

In all particle problems of step 2 of the algorithm,the following additional assumptions are made.The overlap-based model for collisions(equations(10)to(14))requires that the collisions be resolved with small time-steps,such that bothδand ˙δin(10)be accurately computed.Here we use∆t=0.0002 ns,chosen so as to ensure at least five time steps per collision.This value is arrived at by estimating the duration of a typical collision by means of the Hertz’s formula for elastic collisions[Johnson(1985)],and then dividing the result by five:

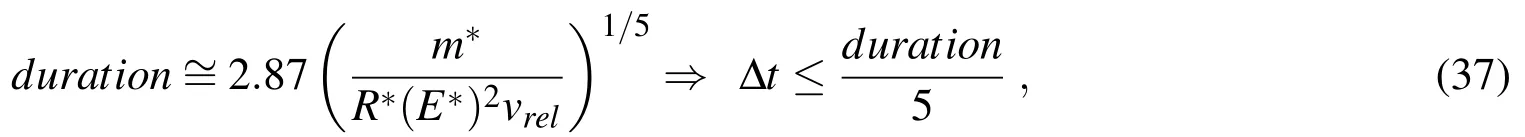
wherevrelis the relative velocity of the colliding pair in the pair’s central direction at the beginning of the collision.The natural frequencies of the lipid bonds,given

As with respect to the cell’s surrounding medium,besides the pressure gradient of equation(21)we assume that particles outside of the cell do not experience any pressure forces,whereas all particles experience drag according to equation(6).A rigid wall is placed at the opposite side of the stream to prevent the cell from undergoing large overall rigid body motions when impacted by the stream.Other data are as follows:

•Mass density of the stream particles=1000 kg/m3=1×10−6fg/nm3;

•Mass density of the membrane particles=900 kg/m3=9×10−7fg/nm3;

•Cell internal pressure force magnitude:=32.7×10−5nN;

•Drag force parameters:cenv=0.000005 nN·ns/nm andvenv=0;

•Spring constant for the lipid bond forces:kij=5×10−3nN/nm;

•Dashpot constant for the lipid bond forces:cij=0.00001 nN·ns/nm;

•Critical strain of circumferential bonds:=0.5;

•Critical strain of radial and cross-wise bonds:=0.1;

•Elasticity modulus of stream and membrane particles(needed to resolve collisions):Ejet=Elipid=100 nN/nm2;

•Poisson coefficient of stream and membrane particles(needed to resolve collisions):νjet=νlipid=0.25;

•Damping rate for particle-particle collisions:ξ=0.1;

•Coefficient of dynamic friction for particle-particle collisions:µd=0.1;

•Gravity is neglected(gg g=o);

•Initial distance between stream front and cell exterior=10 nm;

•Rigid wall properties:µd=0.1 andξ=0.1;

•Time step size=0.0002 ns;

•Final time at the end of each simulation=10 ns.

We adoptM=20 andN=20,which implies a total of 400 simulations.Table 1 presents the results for the coefficients of variation and Table 2 the results for thecorrelation coefficients for five representative sets of simulations with varying means and standard deviations of the input(design)variables.In Table 1,all values are normalized by theCOV’s forφmean(these tended to be the highest when compared to theCOV’s forvandw).The main conclusions that can be drawn from these results are as follows:

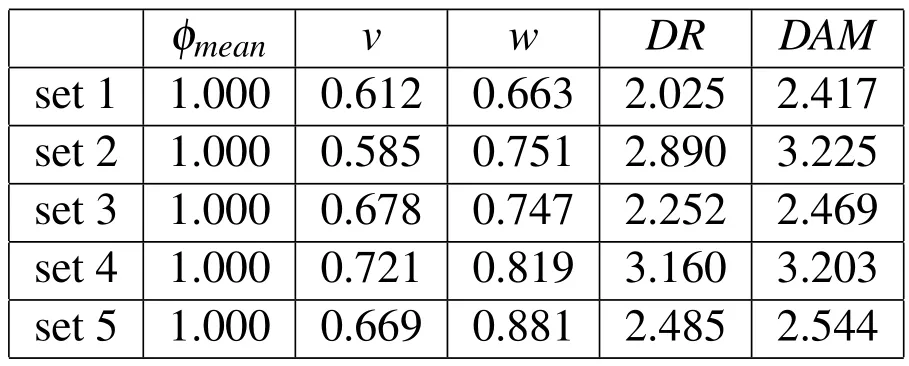
Table 1:Results for coefficients of variation(COV)of input parameters and output results in five representative sets of simulations.Values are normalized by theCOV for the mean particle diameter.

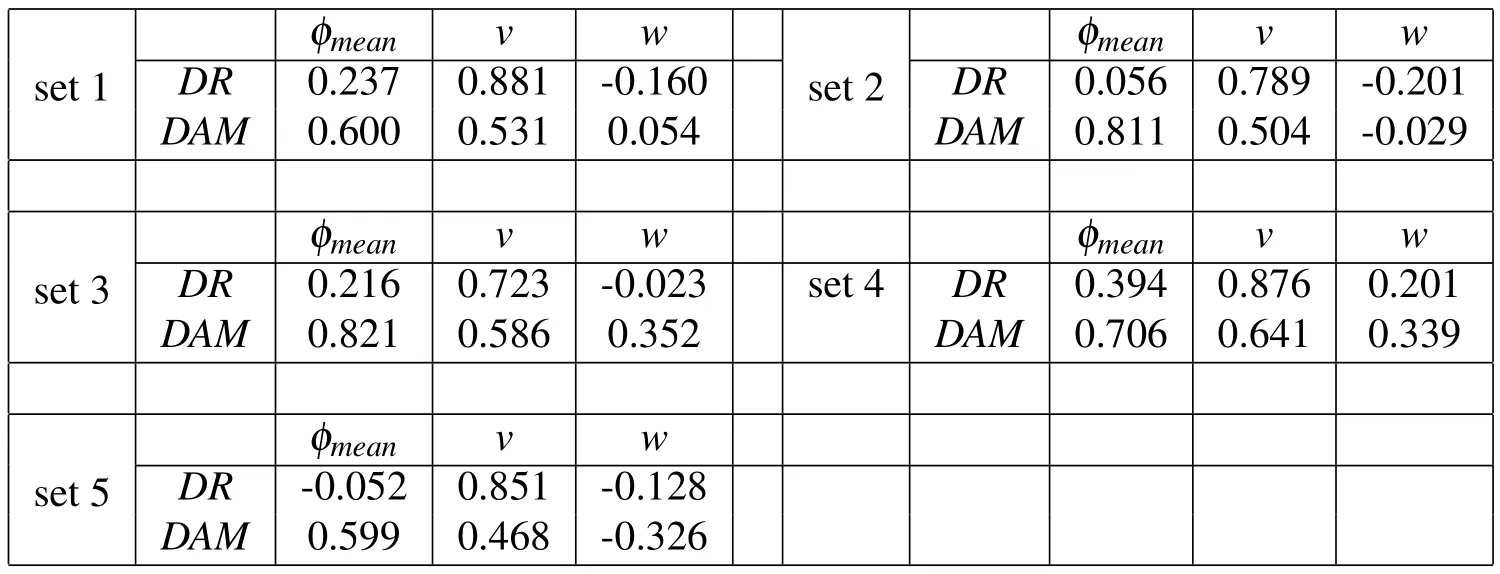
Table2:Results for correlation coefficients(COR)of the output results with respect to each of the input parameters in five representative sets of simulations.

•Variabilities in the mean particle size are more amplified inDAMthan inDR(though the difference is not very pronounced).By similar observations,variabilities in the stream’s velocity show a stronger effect also overDAMthan overDR.

•The coefficients of variation forDRshow a(slightly)wider range of values than those forDAM.This can be partly explained by the more “discrete”nature ofDRas compared toDAM.

•To a first-order estimate,the stream’s velocity is the input parameter that has the most effect onDR,whereas the stream’s mean particle size is the one with the most effect onDAM.The stream’s width,in its turn,proves to have the least effect in all cases.

•The correlation coefficients ofDRandDAMwith respect toφmeanandvtend to be always positive,which means that,to a first-order estimate,increases in these input parameters are accompanied by increases in the output results(and conversely for decreases).

•The correlation coefficients ofDRandDAMwith respect towshow no consistent trend,except that their values are always smaller than those with respect toφmeanandv.

•To a first-order estimate,the stream’s velocity has a stronger influence onDRthan onDAM.This indicates that designs with larger velocities will result in an increase in the delivery rate that is larger than the accompanying increase in the membrane damage.

•To a first-order estimate,the stream’s mean particle size has a remarkably stronger influence onDAMthan onDR.This indicates that designs with larger particles will result in an increase in the membrane damage that is much larger than the accompanying increase in the delivery rate.

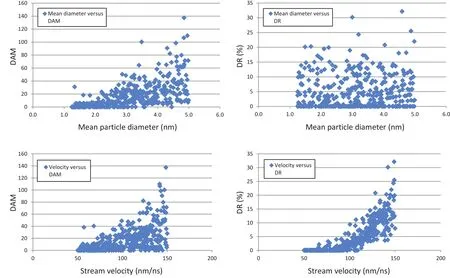
Figure 5:Graphs of output results as a function of input(design)parameters.Results of all 400 simulations are shown.

It is also of interest to investigate which combinations of parameter values inΛlead to the best/worst cases in terms of performance of the delivery system.Such an investigation can be initiated by inspecting graphs such as those on Figs.5 and 6.One can notice,for example by inspecting Fig.6(a),that the highest delivery rates are obtained forv’s ranging from 125 to 150 nm/ns,irrespective of the stream’s mean particle size.At these velocities,from Fig.6(b)one finds that small damage levels are obtained only for streams consisted of small particles(roughly,φmeannot greater than 2.0 nm).Therefore,designs with 125≤v≤150 nm/ns and 1.25≤φmean≤2.0 nm tend to perform more favorably.On the other hand,from Fig.6(a)one realizes that designs withv≤100 nm/ns(roughly)tend to show the lowest delivery rates,especially if they are consisted of small particles.And from Fig.6(b),one may conclude that the highest levels of damage are obtained for designs with medium-to big-sized particles(roughly,φmean≥2.5 nm)and moderate to large velocities(v≥75 nm/ns).Snapshots of deformed con figurations of the cell when impacted by the stream in a typical simulation can be found in Fig.7.

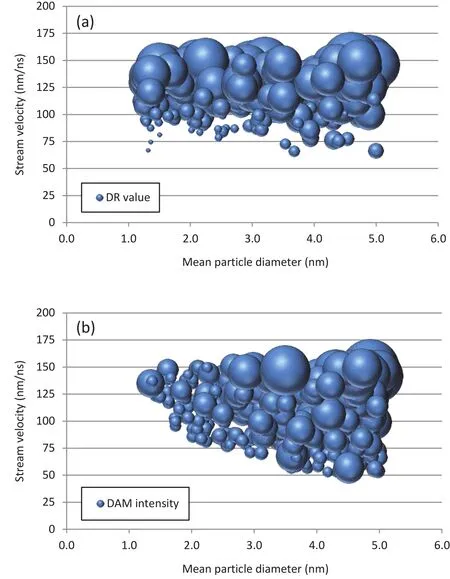
Figure 6:Bubble graphs of output results.The size of the bubbles is proportional to the result’s value.(a)DR as a function of mean particle diameter and stream velocity.(b)DAM as a function of mean particle diameter and stream velocity.Results of all 400 simulations are shown.

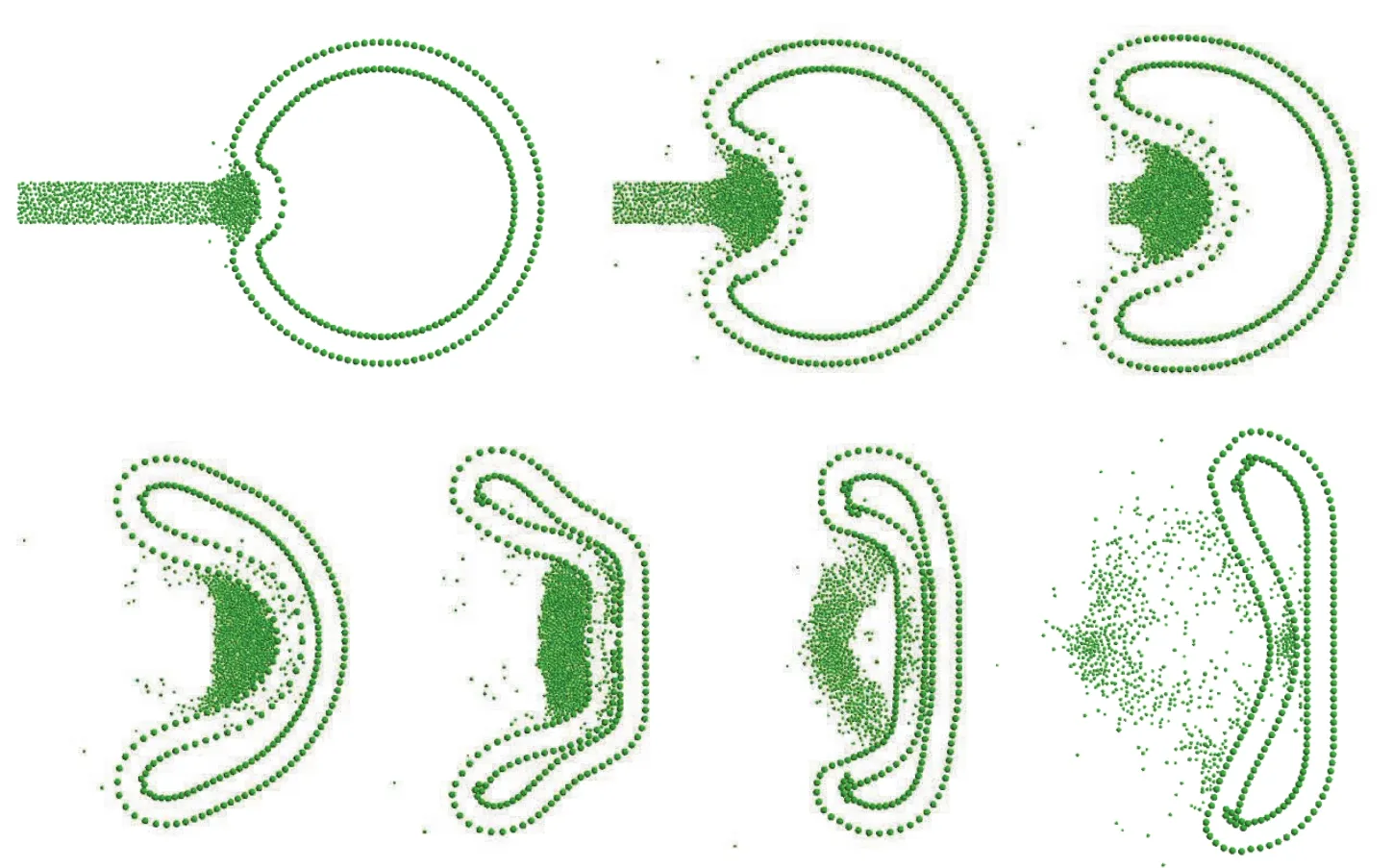
Figure 7:Sequence of snapshots(deformed con figurations)of the cell upon bombarded by the stream in a typical simulation(sequence is from left to right,top to down).Results shown are for φmean=0.65 nm,v=136 nm/ns and w=16 nm.

It must be said,though the above observations are helpful to identify basic or preliminary trends of the system,that it may not be possible to find a unique“minimum”or“maximum”among all possible combinations of parameter values.In this context,a more rigorous approach for the investigation of best/worst scenarios would be by using non-convex,non-derivative optimization algorithms(e.g.genetic algorithms)based on an objective function that includesDRandDAMas arguments.This is not done in the current paper and is left here as a suggestion for future work.

6　Closing Remarks

The main purpose of this work was to present a basic computational framework for parametric simulation and design evaluation of particle bombardment systems intended to deliver substances into cells.It is grounded on a random sampling scheme for selected design parameters combined with a particle-based(discrete element)method for description of the mechanical problem.It can be implemented with small effort by researchers interested in the field.The main advantages of such an approach are that the overall(collective)behavior of these systems can be qualitatively studied in a wide range of parameter values,and yet at a relatively little computational cost.It allows for the identification of basic trends of the system upon changes on the design parameters,and offers a good picture for investigation of best/worst case scenarios.

We remark that our intention here was simply to show how the framework works from a general perspective.To this end,we have selected as design parameters only the stream’s mean particle size,width and incoming velocity.Of course,the influence of other parameters could have been studied as well,such as the cell’s internal pressure,bonding stiffnesses,friction coefficients,etc.These quantities could have also been treated as random variables and have the effects of the variabilities of their values assessed.

Kernel density estimation techniques(e.g.with a Gaussian kernel)can be used to construct the probability distribution functions of bothDRandDAM.This can be straightforwardly done from the mean values of these output parameters in randomly selected sets of simulations.From the generated distributions,probabilities of excellence of speci fied thresholds ofDRandDAM(e.g.the probability that the value ofDAMis higher than a given value)can be obtained.This can be very useful information.Also,based on these distributions one may de fine an index of success(or,equivalently,an index of failure)to quantify how well a cell will respond upon impact by a stream of particles with given design parameters(or,in other words,how well a delivery system with given design parameters will succeed in delivering substances to the interior of a cell).

Particle-based computational models allow for the construction of rapid simulation tools.We believe they are a very useful approach for design evaluation of delivery mechanisms,lessening the number of(costly and delicate)physical experiments and thus helping advance the design of particle-gun delivery systems.

Acknowledgement:This work was supported by FAPESP(Fundação de Amparo à Pesquisa do Estado de São Paulo),under the grant 2012/04009-0(which made possible a research stay for the first author at the University of California at Berkeley,on a sabbatical leave from the University of São Paulo),and by CNPq(Conselho Nacional de Desenvolvimento Científico e Tecnológico),under the grant 303793/2012-0.Material support and the stimulating discussions in CMRL(Computational Materials Research Laboratory,Department of Mechanical Engineering,UC Berkeley)are also gratefully acknowledged.

Andoh,Y.;Okazaki,S.;Ueoka,R.(2013):Molecular dynamics study of lipid bi-layers modeling the plasma membranes of normal murine thymocytes and leukemic GRSL cells.Biochim Biophys Acta,vol.1828,no.4,pp.1259-1270.

Axelsson,A.(1994):Iterative solution methods.Cambridge Univeristy Press.

Bicanic,N.(2004):Discrete Element Methods.Encyclopedia of Computational Mechanics,Volume 1:Fundamentals.Stein E,de Borst R,Hughes TJR(eds).John Wiley&Sons.

Campello,E.M.B;Zohdi,T.I.(2014):A computational framework for simulation of the delivery of substances into cells(DOI:10.1002/cnm.2649).International Journal for Numerical Methods in Biomedical Engineering.

Campello,E.M.B.(2014):Computational modeling and simulation of rupture of membranes and thin films(accepted for publication).Journal of the Brazilian Society of Mechanical Sciences and Engineering.

Cundall,P.A.;Strack,O.D.L.(1979):A discrete numerical model for granular assemblies.Geotech,vol.29,pp.47–65.

Delemotte,L.;Tarek,M.(2012):Molecular dynamics simulations of lipid membrane electroporation.J Membr Biol,vol.245,no.9,pp.531-543.

Duran,J.(1997):Sands,Powders and Grains:An introduction to the physics of granular matter.Springer.

Hac,A.E.;Seeger,H.M.;Fidorra,M.;Heimburg,T.(2005):Diffusion in Two-Component Lipid Membranes–A Fluorescence Correlation Spectroscopy and Monte Carlo Simulation Study.Biophys J,vol.88,pp.317-333.

Israelachvili,J.N.(2011):Intermolecular and surface forces.Elsevier.

Johnson,K.L.;Kendall,K.;Roberts,A.D.(1971):Surface energy and the contact of elastic solids.Proc R Soc Lond A,vol.324,pp.301–313.

Johnson,K.L.(1985):Contact Mechanics.Cambridge University Press.

Khelashvili,G.;Weinstein,H.;Harries,D.(2008):Protein diffusion on charged membranes:A dynamic mean- field model describes time evolution and lipid reorganization.Biophys J,vol.94,pp.2580-2597.

Klein,T.M.;Wolf,E.D.;Wu,R.;Sanford,J.C.(1987):High-velocity micro-projectiles for delivering of nucleic acids into living cells.Nature,vol.327,pp.70-73.

Lennard-Jones,J.E.(1924):On the Determination of Molecular Fields.Proc.R.Soc.Lond.A,vol.106,no.738,pp.463–477.

Mukherjee,D.;Zohdi,T.I.(2014):Rapid parametric simulations for design evaluation and uncertainty characterization of a porous material layer impacted by a particle(accepted for publication).International Journal of Impact Engineering.

Pastor,R.W.;Venable,R.M.(1993):Molecular and stochastic dynamics sim-ulations of lipid membranes.In:van Gunsteren WF,Weiner PK,Wilkinson AK(Eds.).Computer Simulation of Biomolecular Systems:Theoretical and Experimental Applications,Chap.2,pp.443-464.Escom Science Publishers.

Pastor,R.W.(1994):Molecular dynamiscs and Monte Carlo simulations of lipid bilayers.Curr Opin Struct Biol,vol.4,pp.486–492.

Pöschel,T.;Schwager,T.(2004):Computational Granular Dynamics.Springer.Rangamani,P.;Agrawal,A.;Mandadapu,K.K.;Oster,G.;Steigmann,D.(2013):Interaction between surface shape and intra-surface viscous fl ow on lipid membranes.Biomech Model Mechanobiol,vol.12,pp.833-845.

Sanford,J.C.;Klein,T.M.;Wolf,E.D.;Allen,N.(1987):Delivery of substances into cells and tissues using a particle bombardment process.Particulate Science and Technology:An International Journal,vol.5,pp.27-37.

Tieleman,D.P.;Marrink,S.J.;Berendsen,H.J.C.(1997):Computer perspective of membranes:molecular dynamics studies of lipid bilayer systems.Biochim Biophys Acta,vol.1331,pp.235–270.

Wang,Y.;Sigurdsson,J.K.;Brandt,E.;Atzberger,P.J.(2013):Dynamic implicit-solvent coarse-grained models of lipid bilayer membranes:Fluctuating hydrodynamics thermostat.Phys Rev E,vol.88,pp.023301-1-5.

Wellmann,C.;Wriggers,P.(2012):A two-scale model of granular materials.Comput Methods Appl Mech Engrg,vol.205–208,pp.46–58.

Zhang,G.;Torquato,S.(2013):Precise algorithm to generate random sequential addition of hard hyperspheres at saturation.Phys Rev E,vol.88,pp.053312-1-9.

Zohdi,T.I.(2012):Dynamics of charged particulate systems:Modeling,theory and computation.Springer.