基于Taguchi方法的动力总成悬置系统稳健优化*

张代胜，张 旭，王 浩，王 栋，沈 勇，周 舟

(1.合肥工业大学机械与汽车工程学院，合肥 230009;2.上海汽车集团股份有限公司技术中心，上海 201804;3.安徽江淮汽车股份有限公司，合肥 230009)

前言

动力总成悬置系统除支撑发动机和变速器等部件外，还隔离发动机振动向车架以及路面与轮胎振动通过车架向动力总成的传递［1］。随着汽车轻量化技术的日渐成熟，动力总成占整车的质量比越来越大，发动机对总车振动的影响有所提高，并且驾驶员和乘客对汽车舒适性的要求不断提高，所以正确地建立动力总成悬置系统模型，并合理地选择悬置参数就显得尤为重要［2］。

稳健性是指产品性能相对不确定性因素(使用环境和产品本身参数)的不敏感性。稳健性优化设计的基本思想是承认质量特性波动的存在，在不增加制造和使用成本的前提下，通过调整可控设计变量(如几何尺寸、材料特性和安装使用等)的名义值与控制其容差大小来控制零部件质量，从而改善产品质量，降低使用成本。

在优化悬置系统参数时，传统的优化方法过度依赖梯度信息，对于悬置系统这样复杂的数学模型并不适用;遗传算法虽然全局搜索能力强，且不需要梯度信息，节省迭代时间，但要想取得较好的结果需要较高的迭代次数，这就造成了部分参数过度贴近约束边界，得不到较合理的参数分布［3］。本文中首先采用遗传算法获得目标值较好的群体，然后选取一个参数分布合理的个体，应用Taguchi方法进行一次或多次的稳健优化，得到最终结果。

1 悬置系统数学模型

由于车架和动力总成的固有频率远远大于悬置系统的固有频率，故将车架和动力总成视为刚体;假定橡胶件的弹性是线性的，并可忽略其阻尼，建立6自由度动力总成4点悬置模型［4］，如图1所示。

图中O－XYZ为发动机动力总成质心坐标系，O为动力总成质心，X轴平行于发动机曲轴轴线指向发动机前端，Z轴通过发动机总成质心垂直向上，Y轴方向由右手定则确定;前悬置点1、2，后悬置点3、4;u、v、s为悬置的3条弹性主轴方向。则可得广义坐标 q={x，y，z，θx，θy，θz}。

由拉格朗日方程可得悬置系统的振动方程为

式中:M为系统的质量矩阵;C为系统的阻尼矩阵;K为系统的刚度矩阵;q为广义坐标;F(t)为系统所受的激振力。

方程可简化为

由式(2)可得动力总成悬置系统的固有频率ωj(j=1，2，3，4，5，6)和固有振型 φ。

2 能量解耦法

通常6自由度汽车动力总成悬置系统的6个固有振型在多个自由度方向上是耦合的，在某个自由度方向受到激振都可能引起耦合振动，这样会导致共振频带加宽，共振的机会加大。能量解耦法是在得到悬置系统的6个固有模态后，根据能量分布判断动力总成悬置系统是否解耦及其解耦的程度，然后通过修改悬置参数提高系统在某些方向上的解耦率［5］。

当系统以第j阶模态振动时，定义能量分布矩阵的第k行l列元素为

式中:k，l，j=1，2，3，4，5，6;φ(k，j)、φ(l，j)分别为第j阶振型的第k个和第l个元素;M(k，l)为系统质量矩阵的第k行、第l列元素;ωj为第j阶固有频率。

当系统以第j阶模态振动时，第k个广义坐标分配能量占系统总能量的百分比为

若Q(j，k)=100%，则系统做第j阶振动时能量全部集中在k对应的广义坐标上，此时该模态振动完全解耦。

3 优化模型

3.1 设计变量

影响发动机悬置系统特性的参数很多，例如悬置系统的安装位置、安装角度和悬置橡胶的主刚度值等。综合车架和动力总成设计限制，本文中以悬置点处悬置橡胶的各向主刚度值ki(i=1，2，…，n)(n为悬置刚度个数)为设计变量。选用悬置系统4个悬置点，悬置刚度左右一致，共6个设计变量。

3.2 约束条件

(1)频率约束 悬置系统的最大固有频率必须小于发动机自身激励频率f的，才能起到隔振效果;另外，为了避开路面激励频率，悬置系统最小频率应大于 5Hz，即

(2)刚度约束 一方面为了限制发动机的位置移动，要求悬置系统刚度不能太小;另一方面为了使系统具有较好的隔振性能，要求悬置系统刚度不能太大，即 kimin≤ki≤kimax(i=1，2，…，n)［7］。

3.3 目标函数

以实现悬置系统6自由度解耦率最大为目标进行优化设计，把多目标优化转化成单目标优化。优化目标函数为

式中:Qi为各自由度上能量百分比;αi为加权因子。

4 基于遗传算法的悬置系统初步优化

针对某客车发动机，4点悬置，左右对称分布，动力总成参数如表1所示，优化前各悬置点三向主刚度值如表2所示［8］。

表1 动力总成系统参数

表2 各悬置点主刚度值 N·mm－1

根据表1和表2数据，应用Matlab软件计算优化前动力总成悬置系统的6个固有频率和各自由度下的解耦率，如表3所示。

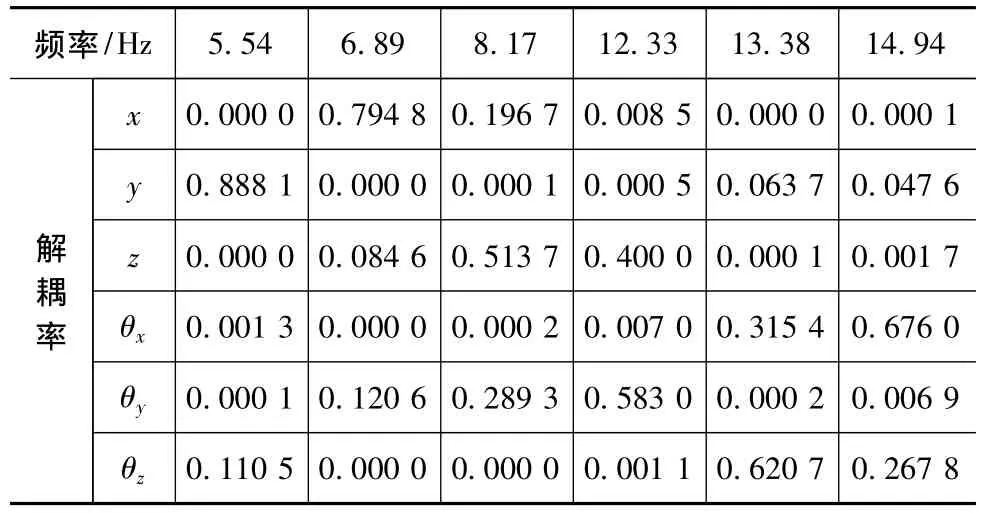
表3 优化前悬置系统固有频率和解耦率

从表3可以看出，6个自由度方向上的解耦率分别是 79.48%、88.81%、51.37%、67.60%、58.3%和62.07%，均在90%以下，解耦率明显偏低。各自由度之间存在严重的耦合。

采用遗传算法对上述悬置系统进行优化，编码方式为25×n的二进制串，个体数目为100，代沟为0.9，为了防止优化结果过分地贴近约束边界值，设置迭代次数为100，从最终种群中选取初步优化结果如表4所示，并计算初步优化后的刚度值对应的固有频率和各解耦率如表5所示。

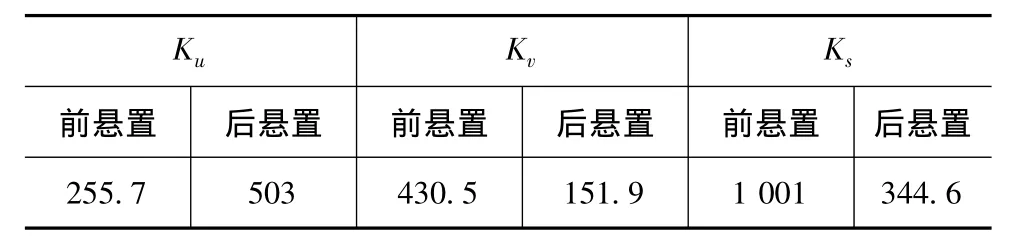
表4 初步优化后各悬置点主刚度值N·mm－1

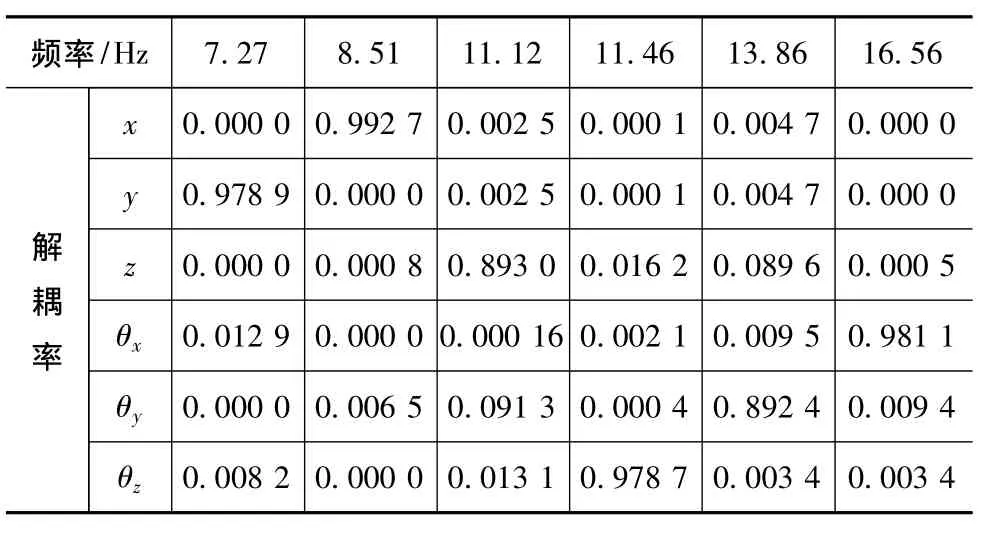
表5 初步优化后系统固有频率和解耦率

由表5可知，经过遗传算法初步优化后，各自由度方向上的解耦率得到显著提高，但z、θy自由度上的解耦率仍小于90%，还存在进一步优化的空间。

5 基于Taguchi悬置系统稳健优化

Taguchi参数最优化设计方法是一种利用正交表来挑选实验条件和安排实验的实验方法，其优点是利用最少的实验数据得到设计参数的最佳组合，实现最优化设计［9］。

信噪比(ηsn)一般作为通信系统的质量指标，用于系统或产品的开发设计。对于质量特性服从Y～N(μ，σ2)分布的产品，可将信噪比定义为η'=μ2/σ2，用来评定产品质量特性的稳定性。为了使η'更加接近正态分布，使效应基本具有线性可加性，将 η'值转化成分贝(dB)值，即 ηsn=10lgη'。

望小特性值是希望Y越小越好，也等价于μ2，σ2越小越好;因此，可令望小特性值η'的比值为

转换成分贝值表示为

此即为望小特性信噪比的计算式。

本文中优化变量的质量特性服从正态分布，并且特性值越小越好，属于望小特性。对第4节的优化结果应用Taguchi方法进一步稳健优化，优化流程图如图2所示。

5.1 制定可控因子水平

选择悬置刚度为稳健设计变量，悬置系统左右对称，共6个设计变量。在经过遗传算法初步优化后，优化结果已非常接近最优解，最优解基本不会超出初步优化结果±10%范围。每个设计变量在设计空间内选取5个设计水平，分别为初步优化结果的90%、95%、100%、105%、110%，具体数值见表6。

表6 可控因子取值水平表 N·mm－1

5.2 制定正交表

在悬置系统Taguchi稳健优化中，不存在偏差噪声源参数，只须设计内表，即正交表。刚度参数采用正交实验设计，根据设计参数的个数(6个)与水平数(5个)，选择L25(56)正交表建立实验分析矩阵，共须进行25次仿真，根据实验分析矩阵和可控因子水平，在Matlab环境中仿真，得到优化函数目标值，即响应值，如表7所示。

5.3 内表数据统计分析

表7 Taguchi实验设计正交表

根据表7数据对仿真的响应值进行汇总分析，得出响应值响应表(见表8)和响应值主效应图(见图3)。

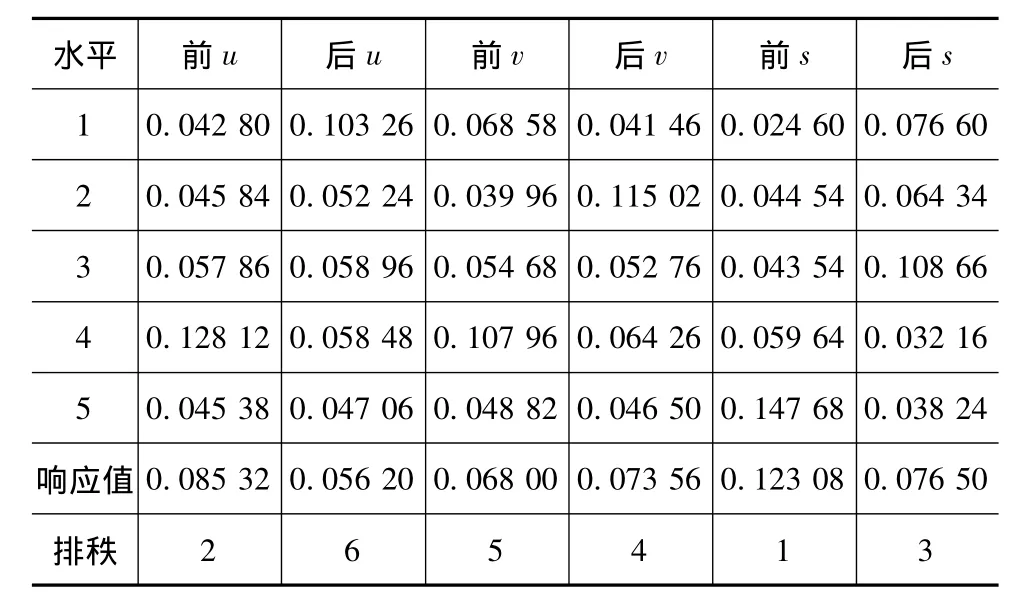
表8 质量特性响应值响应表

计算信噪比，对信噪比进行汇总分析，得出信噪比响应表(表9)和信噪比主效应图(图4)。

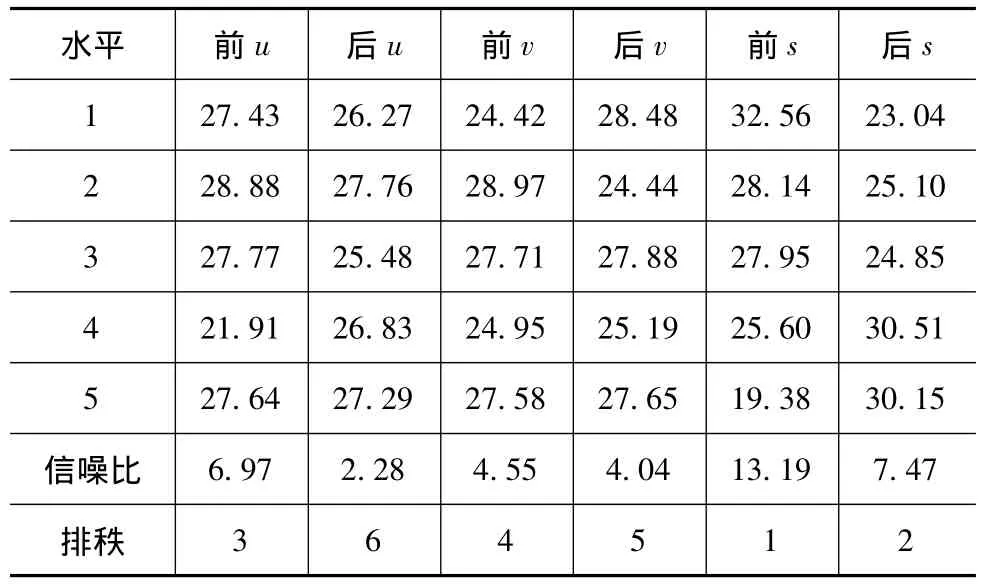
表9 信噪比响应表

5.4 确定建模因子

通过对内表数据的统计分析，可以明显地看到不同位置、不同水平的刚度参数对质量特性值(响应值)和信噪比的影响。响应值越小，说明悬置系统的解耦率越高;信噪比越大，说明悬置系统的稳健性越高，对于表8和表9中刚度参数排序越靠前，说明对悬置系统的贡献率越大，在选择或以后改变时更应慎重。综合考虑解耦率与稳健性方面的要求，各刚度参数水平分别选择水平2(前u)、水平5(后u)、水平2(前v)、水平1(后v)、水平1(前s)、水平4(后s)，具体刚度值见表10。

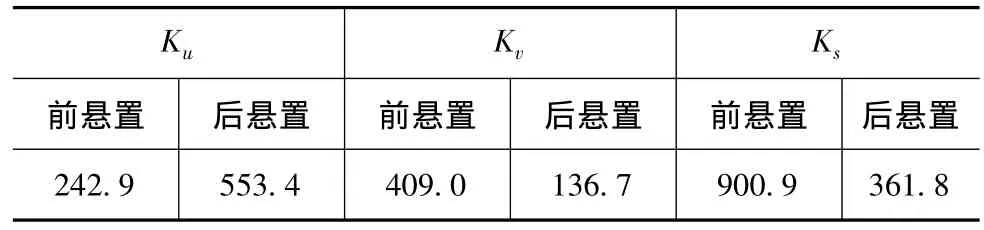
表10 Taguchi方法优化后的刚度值N·mm－1

根据以上刚度值计算出应用Taguchi方法稳健优化后的悬置系统固有频率与解耦率，见表11。

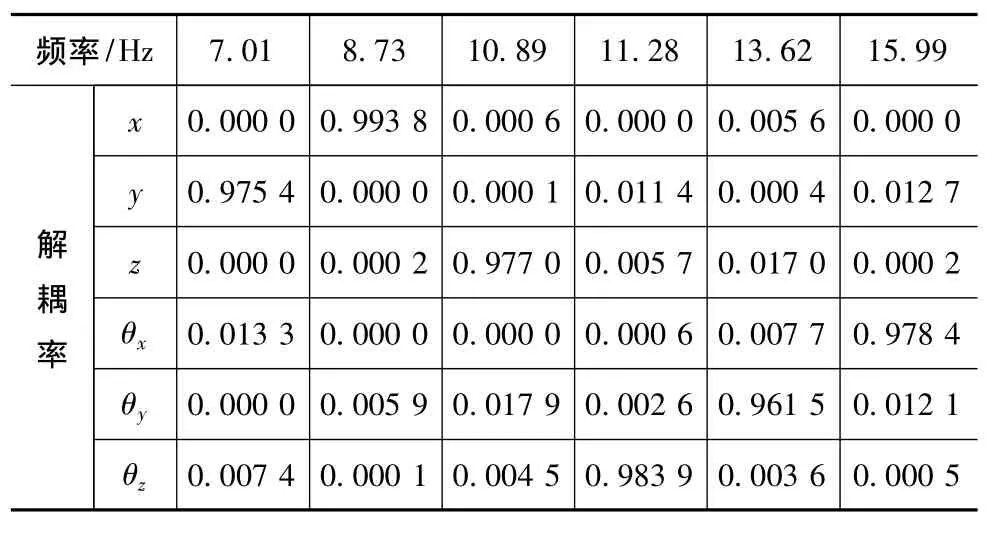
表11 Taguchi方法优化后固有频率和解耦率

比较应用Taguchi方法优化后的结果与遗传算法初步优化的结果发现，在垂向(z)和俯仰(θy)自由度上解耦率均有8%左右的提高，优化结果比较令人满意，如果得到的结果无法令人满意，可把优化后得到的刚度值作为可控因子采用Taguchi方法进一步优化，直到获得满意结果为止［10］。

6 基于Monte Carlo的稳健分析

在一系列生产与使用一段时间后的悬置垫样品中随机抽样检测发现，各向悬置主刚度基本在±12%范围内波动，且分布曲线成正态分布。分别对优化前，初步优化和 Taguchi方法优化结果应用Monte Carlo法进行稳健性分析，分别基于目标函数建立标准差为12%的响应面模型，优化前各向刚度值分布为:k1～N(384，46.1)，k2～N(155.6，18.7)，k3～ N(168.1，20.2)，k4～ N(343.2，41.2)，k5～ N(876，105.1)，k6～ N(154.3，18.5);初步优化后各向刚度值分布为:k1～N(255.7，30.7)，k2～N(503，60.4)，k3～N(430.5，51.7)，k4～ N(151.9，18.2)，k5～N(1 001，120.1)，k6～N(344.6，41.4);Taguchi方法优化后各向刚度值分布为:k1～N(242.9，29.1)，k2～ N(553.4，66.4)，k3～ N(409，49.1)，k4～N(136.7，16.4)，k5～ N(900.9，108.1)，k6～N(361.8，43.4)。经过2 000次随机实验分析，目标函数响应面模型的概率分布分别如图5～图7所示［11］。

对仿真结果进行正态分布拟合，目标函数值g的分布分别为:优化前g～N(0.870 4，0.378 8)，初步优化后 g～N(0.065 2，0.067 1)，Taguchi方法优化后g～N(0.023 5，0.027 6)，结果显示，目标函数均值从0.870 4经遗传算法优化后减小为0.065 2，再经过Taguchi优化后变为0.023 5，两次优化均有显著的提高。通过式(7)分别计算遗传优化和Taguchi稳健优化后的信噪比，结果分别为20.578和28.814，通过对比信噪比可得出悬置系统在稳健性方面提高了40.02%，效果明显。

为进一步了解各自由度上解耦率的稳健性，分别对最终优化后的6个自由度上的解耦率建立响应面模型进行分析，其目标函数是基于单自由度解耦率建立的，消除彼此的影响，其响应面模型概率分布如图8所示。

由图8可见，该优化结果在6个自由度上均有较高的稳健性，优化结果较理想，可应用于实际生产。

7 结论

应用Taguchi方法在遗传算法的基础上构建动力总成悬置系统稳健优化模型，不仅可获得各自由度方向上较高的解耦率，还能保证悬置系统的稳健性，同时避免了传统遗传算法在较高迭代次数下出现过于贴近约束边界的情况发生，具有重要的实际意义。

［1］ 张武，陈剑，夏海．基于灵敏度分析的发动机悬置系统稳健优化模型［J］．汽车工程，2009，31(8):728 －732．

［2］ 李建康，郑立辉，宋向荣．汽车发动机悬置系统动刚度模态分析［J］．汽车工程，2009，31(5):457 －461．

［3］ 夏海，高立新，陈剑．基于伪并行遗传算法的发动机悬置系统解耦优化［J］．汽车工程，2008，30(12):1087 －1090．

［4］ 侯勇，赵涛．动力总成悬置系统解耦设计［J］．汽车工程，2007，29(12):1094－1097．

［5］ 日兆平．能量法解耦在动力总成悬置系统优化设计中的运用［J］．汽车工程，2008，30(6):523 －526．

［6］ Kim Ki Chan，Lee Ju，Kim Hee Jun，et al．Multiobjective Optimal Design for Interior Permanent Magnet Synchronous Motor［J］．IEEE Transactions on Magnetics，2009，45(3):1780 －1783．

［7］ Teek Seng Low，Chen Shixin，Gao Xianke．Robust Torque Optimization for BLDC Spindle Motors［J］．IEEE Transactions on Industrial Electronics，2001，48(3):656 －663．

［8］ 上官文斌，蒋学锋．发动机悬置系统的优化设计［J］．汽车工程，1992，14(2)．

［9］ 刘国兴，任世彬．田口方法与稳健性设计［J］．电工电气，2010(10):53－57．

［10］ Ting Y，Huang JS，Chuang F K．Dynamic Analysis and Optimal Design of a Piezoelectric Motor［J］．IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2003，50(6):601－613．

［11］ 时培成，陈无畏，高立新．基于蒙特卡罗法的动力总成悬置系统稳健设计［J］．汽车工程，2010，32(8):707 －711．