某机载雷达多自由度振动参考谱制定研究
司中柱,刘继承
(南京电子技术研究所,南京 210039)
某机载雷达多自由度振动参考谱制定研究
司中柱,刘继承
(南京电子技术研究所,南京 210039)
本文阐述了一种基于实测振动数据的机载雷达多自由度振动参考谱制定方法。采用坐标变换法,在时域内从结构的加速度响应中提取出结构的刚体自由度振动。通过对结构刚体自由度振动的信号分析,得到各自由度的自功率谱密度(PSD)和各自由度之间的相干函数γ2(f)和相位θ(f),形成多自由度振动试验参考谱矩阵。用此参考谱进行多轴振动环境试验,可真实地模拟机载雷达的实际振动环境。
多自由度振动;参考谱矩阵;坐标转换
引言
军用装备的故障大多数是由振动环境引起的,且这种振动环境是由多自由度振动合成的。目前由于试验设备和技术的限制,在产品的研制阶段,只能分别用垂向和水平方向的单自由度振动试验代替实际的多自由度振动环境,来考核、验证产品的抗振设计。这种方法无法真实地模拟实际振动环境给试验样品带来的应力效应,不能激励出某些只有在多自由度振动环境下才能暴露的故障,导致一些已按规范通过单轴振动环境试验的装备在实际工作环境下仍然故障不断。为了在试验室更真实地模拟多自由度振动环境,近年来,美国TEAM和SD、日本IMV等公司对多自由度振动试验设备、试验控制技术进行研究,取得了较大的进展,其推出的多自由度振动试验系统已能较好地再现多自由度振动环境。美军标MIL-STD-810G方法527也将多自由度振动试验列为正式的试验。但与之相对应的有关多自由度振动试验条件制定、归纳方法的研究却相对滞后,公开发表的文献极少,严重制约了该技术在工程上的运用。
本文对机载雷达多自由度振动试验条件的制定方法进行研究,用坐标转换矩阵法从实测的环境振动信号中提取结构的多自由度刚体振动,并通过对多自由度刚体振动的自功率谱密度、互功率谱密度分析,形成了多自由度振动试验的参考谱—功率谱密度矩阵,为机载雷达的多自由度振动试验提供了依据。
1 自由度的确定
机载雷达尽管结构复杂,但绝大部分雷达单元采用箱式结构,印制板组件垂直插在机箱前后面板的插槽内,并通过安装在印制板组件上的锁紧机构固定。有时在机箱的背部和底部也可能固定有印制板。一般说来,印制板组件对其法向的振动激励最为敏感。如果印制板上安装有质量较大的元器件,那么印制板面内的振动也有可能引起元器件管脚的疲劳损伤,因此机载雷达单元可以通过同时施加三个轴向的平动自由度振动激出故障,相对而言对转动自由度振动不敏感。在可以预见的未来,三自由度系统(如图1)可满足机载雷达产品对多自由度振动试验的需求。
2 多自由度刚体振动信号提取
在多自由度振动试验过程中,最终控制的是多自由度振动系统的刚体自由度,因此,多自由度振动试验的参考谱矩阵是由结构刚体自由度形成的功率谱密度矩阵。但在振动环境测量时,测量的是结构的加速度响应,而不是结构的刚体自由度振动,且测量的通道数也可能远远超过自由度数,因此必须采用某种计算方法,从结构的加速度响应中提取出结构的刚体自由度振动。
采用理论力学原理,通过一个坐标转换矩阵T,可在时域内实现结构刚体自由度振动{c}与结构加速度振动响应{a}之间的相互转换[1][2]:

该坐标转换矩阵T取决于加速度传感器的位置。在对典型机载雷达单元进行环境振动测量时,通常测量机箱底部四个角上的振动,传感器的布置如图2所示。

图1 三自由度(X、Y、Z)振动系统
图中A1、A2、A3、A4的坐标分别为(-r1,-r2)、(r1,-r2)、(-r1,r2)、(r1,r2),则在时域内有:

式中:

分别为实测的加速度时域信号和结构刚体振动加速度信号。如果仅考虑三自由度平动振动,取前三行即可:

由雷达结构的刚体自由度振动{X YZ }-1,即可计算、归纳出多自由度振动试验的参考谱功率谱密度矩阵。
3 试验参考谱的计算
三自由度振动试验参考谱矩阵是一个3×3阶矩阵:

其中对角线上的元素是各自由度的自功率谱密度,反映振动的强度,可容易地由振动信号分析软件估计出来;非对角线元素是各自由度之间的互功率谱密度,反映各自由度之间的相互关系。由于相干函数和相位物理意义更直观和易于理解,因此常用来代替互谱。互谱与相干函数、相位之间可方便地进行换算。

设CSDxy(f)为X、Y轴间的互谱,|CSDxy(f)|、θxy(f)为复数CSDxy(f)的幅值和相位,则CSDxy(f)可用下式表示:


X、Y轴之间的相干函数可由下式计算:xy(f)≤1。(f)为0说明两个轴
向的振动相互独立、互不相干。但在制定试验条件时,相干函数一般取一个非0的小值,如(f) = 0.1,此时相位为随机变量,无需设置;(f)为1说明两者完全相干,但在多自由度振动试验时,(f) =1将导致控制谱矩阵奇异,造成试验无法控制,且在振动环境的实际测量过程中,受测量噪声和结构非线性的影响,两个轴向之间的(f)也不可能为1,因此如果两个轴向振动属强相干,(f)在0.95~0.98之间取值。
4 某型机载雷达多自由度参考谱的制定
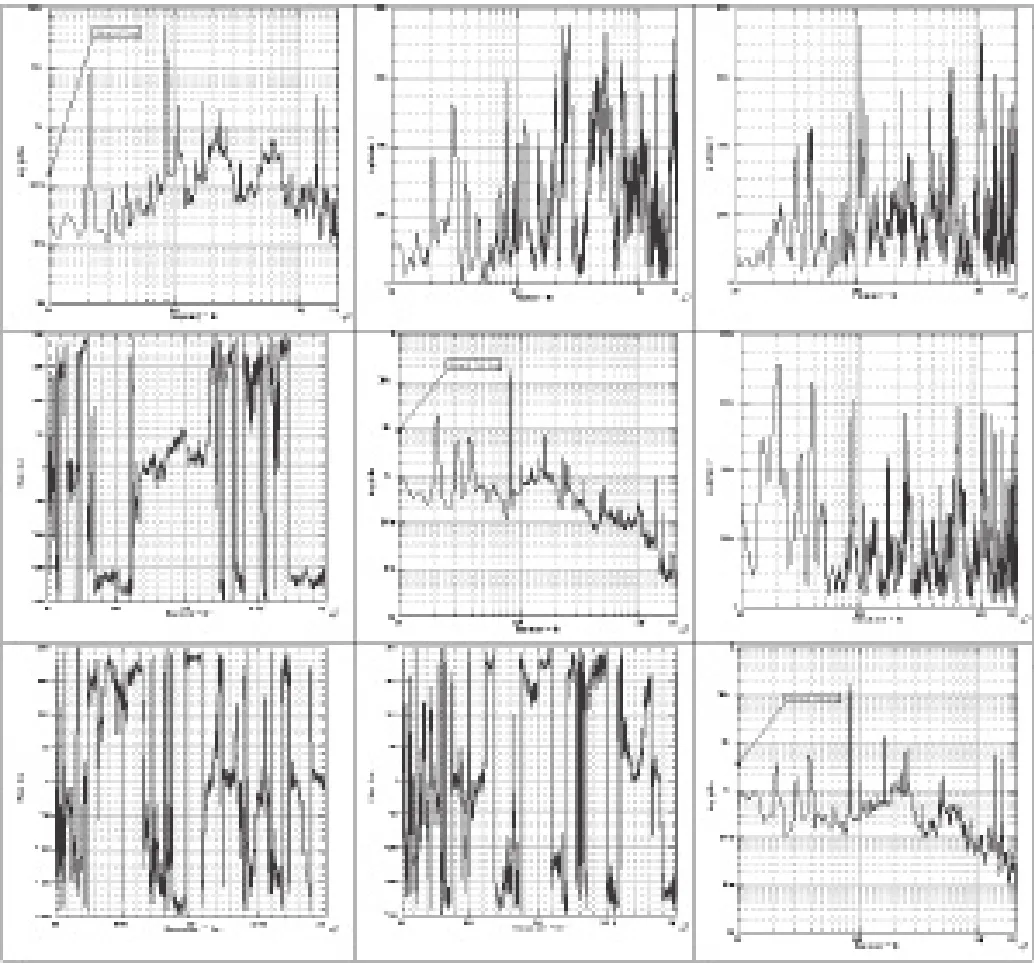
某机载雷达单元(右侧单元)在飞机上的振动测量如图3所示,共测量了3个架次,采样频率为12800Hz,频率分辨率0.7Hz,试验频率范围:10Hz~2000Hz。采用三个平动自由度,计算出参考谱矩阵如图4。图4中,对角线上的是各自由度的自功率谱密度,下三角阵上的是各自由度之间的相位,上三角阵上的是各自由度之间的相干函数。

图3 某机载雷达单元(右侧单元)振动环境测试
相干函数0≤γ2
5 结论
1)用坐标转换法,可从实测的机载雷达结构振动响应中提取出刚体自由度振动。
2)通过对结构刚体自由度振动的信号分析,可估计出多自由度振动试验的参考谱矩阵。
3)试验的加速、装备全寿命周期内所有工况的试验参考谱归纳技术有待进一步研究。
[1] Underwood, M. and Keller, T. Applying Coordinate Transformations to Multi-DOF Shaker Control, Sound and Vibration Magazine, January 2006.
[2] Hale, M and Fitz-Coy, N. On the Use of Linear Accelerometers in Six-DOF Laboratory Motion Replication: A Unifi ed Time-Domain Analysis, 76th Shock and Vibration Symposium, 2005.
Study on Developing Multiple Degrees of Freedom Vibration Reference SDM of Air-borne Radar
SI Zhong-zhu,LIU Ji-cheng(Nanjing Research Institute of Electronics Technology, Nanjing 210039)
This paper describes an air-borne radar MDOF (multiple degrees of freedom) vibration reference SDM (spectrum density matrix) development method based on the measured field data. Using the method of coordinate transformation, the structure vibration of rigid body DOFs can be derived from the measured acceleration responses in time domain. The PSD (power spectrum density) and CSD (cross power spectrum density) terms are estimated by the rigid body vibration data analyzing. The profile SDM can be used for multi-axis vibration testing to simulate a much more accurate environment than that of a single axis testing.
MDOF vibration;reference matrix;coordinate transformation matrix
V216.5
A
1004-7204(2014)01-0048-03
司中柱(1983— ),男,工程师,南京航空航天大学硕士,现在南京电子技术研究所从事可靠性与环境试验方面工作。
刘继承(1965— ),男,研究员,南京航空航天大学博士,现在南京电子技术研究所从事可靠性与环境试验方面工作。

