地震疏散路径规划算法＊

吴正言 张春勤 莫时旭

（桂林理工大学广西矿冶与环境科学实验中心1） 桂林 541004）

（桂林理工大学广西岩土力学及工程重点实验室2） 桂林 541004）

（上海交通大学安泰经济与管理学院3） 上海 200052）

目前，应急疏散交通分配主要采用均衡配流［1－2］的方法，不仅所分配的路径无法保证疏散交通流的安全性，而且算法的计算代价高［3］，缺乏解决突发交通拥堵的应变性.路径行程安排方法则运用网络流和路径搜索算法产生OD路径，以及每条路径疏散交通流的行程安排.可见的文献主要包括考虑时空拥挤度［4］和具有通行能力约束的路径规划方法（capacity constrained route planner，CCRP）［5］.考虑时空拥挤度的实质与考虑通行能力是一致的，但需标定的参数影响因素复杂，可操作性差.而CCRP是最著名的路径行程安排启发式算法，算法的复杂度低、实时性好，能生成近似最优的疏散路径规划方案，并适用于较大规模的路网.但该方法缺少对疏散路径的危险性、可通行性的考虑，并缺少对突发交通拥堵动态生成疏散路径的能力，致使所生成的交通组织方案安全性、可通过性和应变性较差.本文针对地震灾害的交通条件，以CCRP算法为基础，考虑路网的危险性和可通行性，以使应急疏散交通流分配到危险性低且可通行性高的最短路径上.同时，为了提高应急疏散过程中对突发交通拥堵的应变能力，增加了对突发交通拥堵点自动优化生成疏散路径的能力，进而提出地震疏散路径规划（earthquake evacuation route planning，EERP）算法，并进行了实例验证.

1 EERP算法描述

应急疏散路网中节点和连边的通行能力具有非负整数约束，连边还具有非负的行程时间，且其行程时间包括交叉口的延误.假定疏散的总交通量、初始点位置和疏散目的地位置为已知，并假设可实时接收到路网的状况信息，包括路网中的安全节点区域，危险节点或路段，以及突发交通拥堵点等.应急疏散条件下，由于疏散路网的大部分路段处于饱和或过饱和状态，交通流基本不超车，因此，假定连边的交通量具有先入先出的特性.

EERP算法主要包括一系列由疏散原点到目的地的路径，以及路径交通量的时间行程安排，其中路径交通量的时间行程安排要遵守路径中节点和连边的通行能力约束.

EERP在确保疏散危险性较低的前提下，使应急疏散的总时间最小，并使疏散路径规划方案的计算效率满足应急疏散的要求.

2 EERP算法设计

2.1 输入变量的确定

1）路网G（N，E），其中，N 为交叉口集合，E为路段集合.

任意节点n∈N，具有2个属性：交叉口的通行能力NC（n）和需疏散交通量NO（n）.

任意连边e∈E，具有2个属性：路段的通行能力EC（e）和行程时间Tt（e）.

2）疏散原点集合S，S⊆N.疏散原点s∈S，具有需疏散的交通量属性.

3）疏散目的地集合D，D⊆N.疏散目的地节点d∈D，具有可容纳交通量的能力属性ADC（d）.如果节点d没有容纳能力的限制，则ADC（d）＝∞.

4）应急疏散的安全时限TS.如果安全时限不可知，则TS＝∞.

2.2 EERP算法设计步骤

1）检查疏散原点是否具有需疏散的交通量.如果没有交通量则退出程序，反之则进行下一步.

2）路段行程时间的综合评估.为了充分考虑地震疏散中路段的危险性和可通行性，在路段的行程时间中引入危险性和可通行性惩罚函数，即

式中：CTt（e）为路段e的行程时间估计值，其数值与道路的交通状况有关，根据交通量与路段行程时间的关系，采用BPR改进模型［6］计算获得；M为惩罚因子，是充分大的数，表示危险或不可通行的路段，其行程时间充分大；α为路段的危险性惩罚系数；β为路段的可通行性惩罚系数，且α，β∈［0，1］.路段α和β的取值是由其结构状态决定的，而其结构状态会因地震的破坏而发生改变，与路段的地质环境和人工环境等因素有关.α的取值可根据路段所在的地层类型、地下水深度、地质构造、建筑物类型与抗震能力、道路两侧建筑物高度与距离之比、道路上的脆弱点等进行综合评估得到.β的取值与路面的结构、质量有关，可根据路面的损毁程度对可通行性的影响进行评估获得.如果路段e的危险性较小或可通行性较好，则α，β的取值接近于0；反之，如果e危险性较大或可通行性较差，则α，β的取值接近于1.

3）按最短路优先分配规则，运用矩阵迭代算法［11］寻找原点集S到终点集D 的最短路径R＜s，n1，n2，…，nk，d＞，使 R 的行程时间TR≤TS，并得R中各节点ni（i＝1，2，…，k）对应的时间点T＜t1，t2，…，tk＞.同时，R 连边的剩余通行能力AEC和节点剩余通行能力ANC要满足以下条件

4）计算路径R的分配交通量

式中：s为路径R的原点；d为疏散目的地节点，i∈｛1，2，…，k－1｝.

5）计算路径R中连边、节点的剩余通行能力.为表达方便起见，用计算机编程伪代码表示为

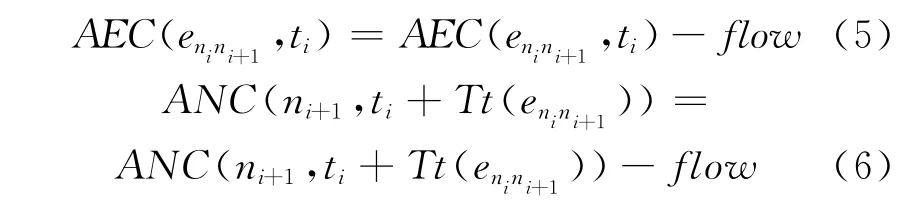
式中：等号表示将右边部分的值赋给左边的变量，i∈｛1，2，…，k－1｝.

6）计算路径R原点剩余的待疏散交通量，以及疏散目的地节点的剩余容纳能力.用计算机编程伪代码表示为

7）如果AEC（enini＋1，ti）＝0或 ANC（ni＋1，ti＋Tt（enini＋1））＝0，则表示连边或节点的交通量已达到其可能通行能力，后面分配的交通量必须多等待1个时间单位，因此，对应连边的当量行程时间自动增加1个时间单位，用计算机编程伪代码表示为

8）如果由于突发的意外情况，致使路径R上点j发生严重的交通拥堵，若j∈enini＋1则增设j为路网虚拟节点，若j∈N则j为路网的实际节点.为疏散此节点j的拥堵交通量，则将节点j并入疏散原点集，作为临时疏散原点，用计算机编程的伪代码表示为

9）如果节点m∈S，且NO（m）＝0，则将节点m从疏散原点集中去除，用计算机编程的伪代码表示为

式中：等号表示将右边部分的值赋给左边的变量.

10）反复执行1）～9），如果安全时限已知，则直到疏散路径行程时间TR＞TS为止；如果安全时限未知，则直到疏散原点集S中的交通量疏散完毕为止.

3 实证分析

按CCRP算法生成的应急疏散路径规划方案如表1所列，为直观起见，将生成的路径标记在疏散路网中，见图1.从中可见，CCRP算法生成的疏散路径依然通过危险节点9和3，不能绕过危险区域，无法满足疏散路径危险性小的前提条件，方案的安全性较差.而且，整个方案的所有规划路径，都没有对突发拥堵的节点8采取任何疏散的措施，缺乏对突发交通拥堵的必要疏散能力.

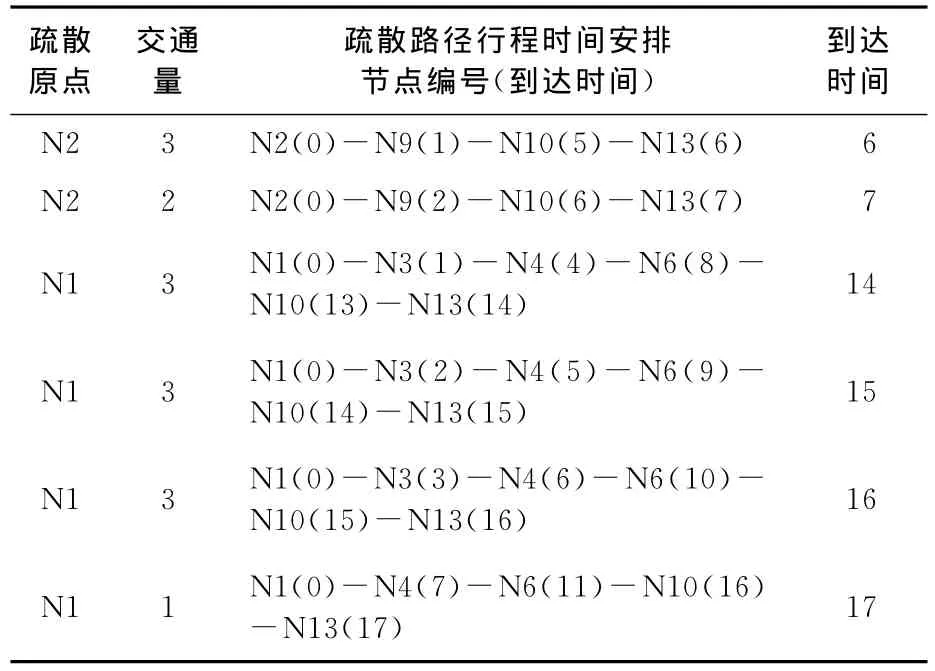
表1 CCRP算法生成的路径规划方案

表2 EERP算法生成的应急疏散路径规划方案

图1 CCRP算法生成的疏散路径图

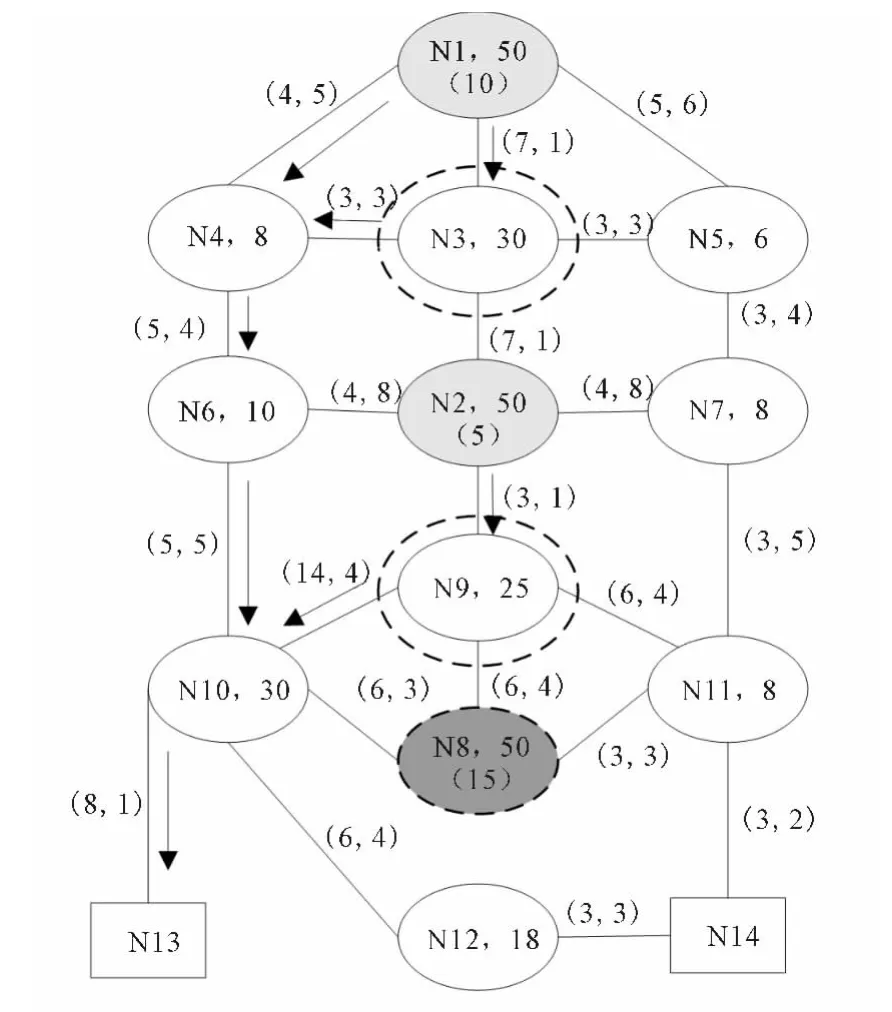
图2 EERP算法生成的疏散路径图

EERP算法生成的路径规划方案如表2所列，将生成的疏散路径规划方案汇总成节点见图2.从中可以看出，EERP算法充分考虑了疏散路网的可通行性和安全性要素，可以绕过危险区域，降低了疏散路径的危险性.而且，对突发交通拥堵点，可按需疏散的交通量动态规划出相应的疏散路径，具有必要的应变性和疏散调整能力.

综上，EERP算法可以弥补CCRP算法在疏散路径安全性和可通行性方面的不足，且对突发交通拥堵具有自动优化生成疏散路径的能力，所产生的应急疏散路径规划方案具有更好的实用性.

4 结束语

针对地震应急疏散的特殊性，在CCRP算法的基础上，考虑了疏散路径的安全性和可通行性要求，并增加了对突发交通拥堵的自动优化生成疏散路径的能力，提出了地震疏散路径规划算法.实证分析表明，EERP算法所规划的路径具有安全性和可通行性好的特点，且对突发交通拥堵具有必要的应变性.为了进一步提高本算法的实用性和可操作性，下一步需进一步研究地震疏散路径的危险性及其可通行性的快速评估方法.

［1］HAN L.D.Global optimization of emergency evacuation assignments［J］.Interfaces，2006，36：502－513.

［2］陈岳明，萧德云.基于动态交通分配的路网应急疏散模型［J］.清华大学学报：自然科学版，2009，49（8）：1102－1105.

［3］LIU X.，HE Xiaozheng，BAN Xuegang （Jeff）.A cell－based many－to－one dynamic system optimal model and its heuristic solution method for emergency evacuation［C］.The 86th TRB Annual Meeting，Washington D.C，USA，2006：1－19.

［4］李清泉，李秋萍，方志祥.一种基于时空拥挤度的应急疏散路径优化方法［J］.测绘学报，2011，40：517－523.

［5］KIM Sangho，GEORGE Betsy，SHEKHAR Shashi.Evacuation route planning：scalable heuristics［C］.Proceedings of the 15th annual ACM international symposium on Advances in geographic information systems，2007，LNCS 3633：1－8.

［6］王素欣，王雷震，高 利，等.BPR路阻函数的改进研究［J］.武汉理工大学学报：交通科学与工程版，2009，33（3）：446－449.