一种基于区间直觉梯形模糊数偏好的大群体决策冲突测度研究

徐选华，万奇锋，陈晓红，周艳菊

(中南大学商学院，湖南 长沙 410083)

1 引言

灾害应急救援过程需要多个相关部门的参与，任何部门和任何个人都不可能具备应急决策所需的综合性知识、信息和经验，因此需要多方面的专家在其相关领域进行配合协调决策，将决策结果进行汇总并根据现场应急情况进行优化，实现群体决策结果的合理和有效[1]。这样，应急决策群体往往不是一两个人组成的小群体，而是一个人数较多的异常复杂大群体(人数不少于20的群体)。群体的人数越多时，其成员间的冲突往往越大，群体成员意见达成一致的难度也就越大。应急决策作为一个典型的多部门协同群决策问题，如何有效地解决决策成员之间意见的冲突性，将不同的个人意见综合成一致的群体意见，是一项需要解决的内容。同时，应急决策的时效性突出，为了避免事故灾害造成更大的损失，须在短时间内作出有效的处理决策，但决策所需的信息往往来不及收集，收集到的信息往往也不一定精确，这使得应急决策变成了一个模糊冲突性决策。

实际的应急决策中，受客观环境的复杂性、决策者的知识结构和专业水平、时间压力等诸多因素的影响，决策依据信息模糊，在这种环境下决策者给出的偏好信息往往是直觉模糊的，于是出现了直觉模糊环境下的多准则群决策问题[2]。直觉模糊数自Atanassov[3]提出以来，由于同时考虑了隶属度、非隶属度和犹豫度三方面的信息，比传统的模糊数在处理模糊性和不确定性等方面更具有灵活性和实用性。因此，偏好信息为直觉模糊集或粗糙集的模糊多准则决策方法被广泛研究[4-6]。其中区间直觉梯形模糊数[7]是直觉模糊数的一种扩展形式，在刻画客观世界的模糊性和不确定性方面，比其他直觉模糊数的扩展更精细和准确[8]，万树平[9]对其运算法则、性质、排序方法进行了研究。在冲突测度方面，自从冲突理论[10]提出之后，大量学者进行了组织或群体冲突方面的研究，已有的研究主要侧重于冲突的定义[11-13]、产生冲突的原因[14-16]、冲突的分类[17-19]以及群体冲突对决策的作用机制[20-21]，对于复杂大群体决策成员偏好之间冲突程度的定量分析仍有待深入研究，本文研究基于区间直觉梯形模糊数的大群体决策冲突测度模型，为大群体偏好集结与决策以及群决策支持系统打下基础，在应急决策中具有一定的实用意义。

2 区间直觉梯形模糊数间的距离

其非隶属函数为：

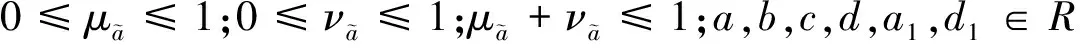
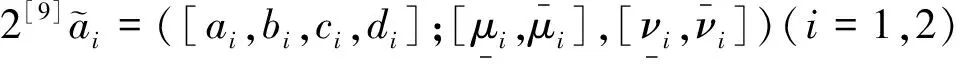
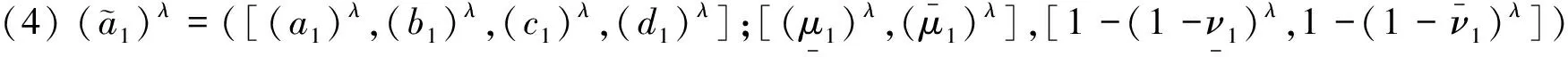
参考徐泽水[22]和王坚强等[23]思路，现基于Hamming距离，给出两个区间直觉梯形模糊数间距离的定义。

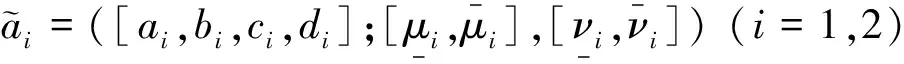
(1)

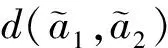
在实际决策过程中，两区间直觉梯形模糊数距离表示两决策成员偏好之间的差距，当两区间直觉梯形模糊数距离为0时，说明两名决策成员的偏好相同，决策结果一致；而当两区间直觉梯形模糊数距离为1时，说明两名决策成员间偏好相差最大，决策结果完全相反。

3 大群体偏好冲突测度

3.1 群体成员冲突函数

定义5 决策成员冲突函数。群体Ω中决策成员i1和决策成员i2的冲突函数为：

(2)

其中ωj为第j个决策属性的权重。

3.2 基于冲突的大群体成员偏好聚类

群体规模对决策质量是有影响的，设计群决策支持系统时首要考虑的因素就是群体规模。已有研究表明群体决策中5～10人最有效，能得出较正确的结论。当决策群体人数为2～5人时能得到一致意见[26]。应急决策中，为了尽快得到大群体意见的一致，我们可以先把大群体分成人数相对较少的几个聚集，先统一聚集的意见，再统一大群体的意见。这种方法比直接统一大群体的意见能更有效的得到一致意见。

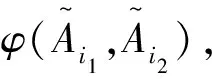
3.3 群体冲突测度

由于大群体的偏好已经聚类成一些偏好聚集，而每个聚集内部的成员冲突相对较小，因此首先利用群体成员冲突函数获得各个聚集的冲突度。对于群体Ω中的聚集Ck，其冲突度指标ρk为：

(3)

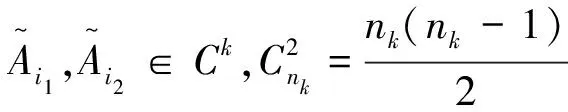
再利用各个聚集的冲突度结合聚集的规模综合成整个大群体的冲突度。对于群体Ω，其冲突度是各个聚集冲突度的综合，Ω冲突度指标ρ为：

(4)

群体的冲突度受群体中大聚集冲突度的影响较大。如果群体中只有一个聚集，则该群体的冲突指标为0，被认为几乎没有冲突。当聚集个数大于1时，该群体的冲突指标就会大于或等于0，被认为群体的冲突上升。

4 大群体偏好集结

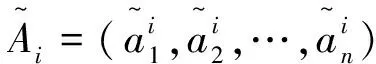
步骤1：决策成员偏好数据标准化，转入步骤2。

步骤2：确定各属性的权重。这里的属性权重我们根据熵理论[24]给出：

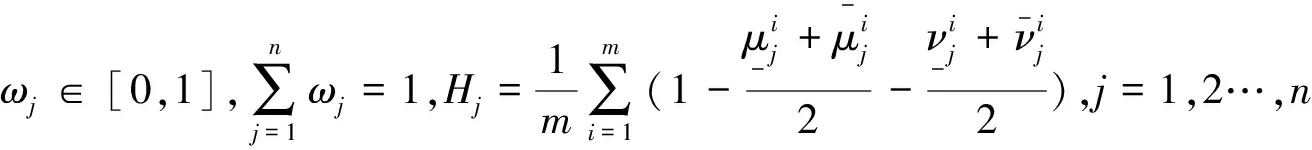
(5)

步骤4：用(3)式计算各聚集的冲突度ρk，利用(4)式计算整个大群体的冲突测度。当ρ>γ时，转入步骤5，否则转到步骤6。

(6)

步骤6：集结整个大群体的偏好，即利用各个聚集的偏好矢量计算群体偏好矢量：

(7)

在偏好集结过程中，阈值γ是群体可容忍的冲突度，可根据具体情况预先选定一个值，其取值越小越好。λi为需修正偏好的决策成员保留其原始偏好的程度，在[0,1)的范围内，λi越大，则修正后的偏好与原始偏好越接近，实际应用中可由该成员自行决定大小，这样保证了决策的柔性，根据文献[26]，一种较好的方法是取容忍冲突度阈值与群体冲突度的商λi=γ/ρ。

集结出的群体偏好矢量是整个决策大群体对某一个方案的综合偏好，是经群体协调之后集体认可的一种偏好表示。当方案不只一个时，可根据文献[9]中区间直觉梯形模糊数的多属性决策方法，依据群体偏好对方案排序，从而选出最优方案。

5 算例分析

(1) 取容忍冲突度阈值γ=0.12，编制上述基于冲突的群体成员偏好聚类算法计算机程序，聚类执行结果如表2所示。

利用(4)式计算得群体冲突度为ρ=0.1085，小于=0.12，即群体的冲突度在可容忍的范围内，无需进行偏好的修正，利用(7)式计算得整个群体偏好矢量为：

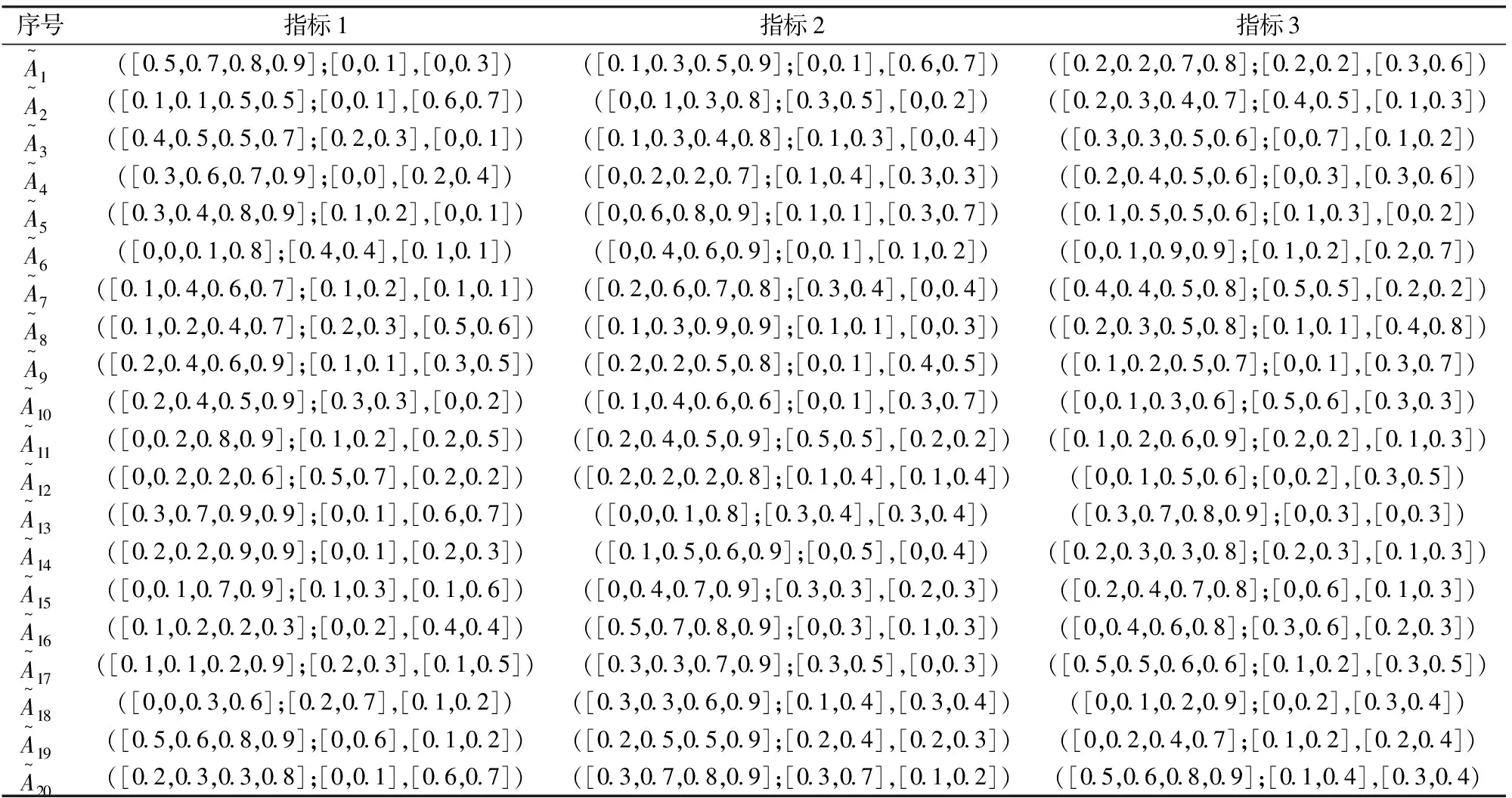
表1 群体成员的偏好矢量表

表2 决策成员偏好聚类结果(γ=0.12)

表3 决策成员偏好聚类结果(γ=0.1)

表4 决策成员偏好修改后的聚类结果(γ=0.1)

表5 各方案的综合直觉模糊数(IITFN-WAA集成)

利用(4)式计算得群体冲突度为ρ=0.1190，大于γ=0.1，群体的冲突度超出可容忍的范围，需进行偏好修正，此处取λi=γ/ρ=0.8401，按步骤5的方法进行群体成员偏好修正。修正后继续进行聚类算法，聚类结果如表4所示。

再次利用(4)式计算群体的冲突度ρ=0.0999，小于γ=0.1，即群体的冲突度在可容忍的范围内，利用(7)式计算得群体偏好矢量为

群体偏好矢量是整个决策群体经协调后集体认可的一种偏好，表达了决策群体对方案“优秀”的认可程度。若决策方案不只一个，为简单起见我们假设还有另外两个方案，决策群体对方案的偏好信息见附录表1和表2。统一取容忍冲突度阈值=0.1，重复上面的大群体偏好集结步骤，方案2经过2次修正，方案3经过1次修正，分别得到另外两个方案的群体偏好矢量如下：

根据文献[9]中区间直觉梯形模糊数的多属性决策方法，得到各方案的综合IITFN以及得分函数与精确函数，结果如表5所示，方案的排序为：方案3>方案2>方案1。最优方案即为方案3。

6 结语

复杂大群体决策中，决策者的偏好信息为区间直觉梯形模糊数普遍存在于决策实践中。本文利用区间直觉梯形模糊数的有关结果，给出了两个区间直觉梯形模糊数的距离，提出了两个成员之间的冲突函数，通过基于该函数的大群体偏好聚类形成聚集结构，各个聚集内部的成员偏好冲突相对较小，而聚集之间的偏好冲突可能较大。在此基础上提出了聚集的冲突测度模型和群体的冲突测度模型，并应用到大群体偏好集结中。相比万树平[9]，汪新凡等[27]，本文方法适用于决策成员较多时的大群体决策和冲突协调；相比徐选华等[28-29]，本文方法考虑了决策依据信息的模糊性与决策者偏好信息的直觉模糊性，更加准确。该模型便于大群体意见的分析与协调，适用于群决策支持系统，在应急决策中具有实际应用价值。同时，本文也有待进一步完善，阈值的选取仍然需要人工摸索，如何更好的给出适当的阈值有待进一步解决。

附录

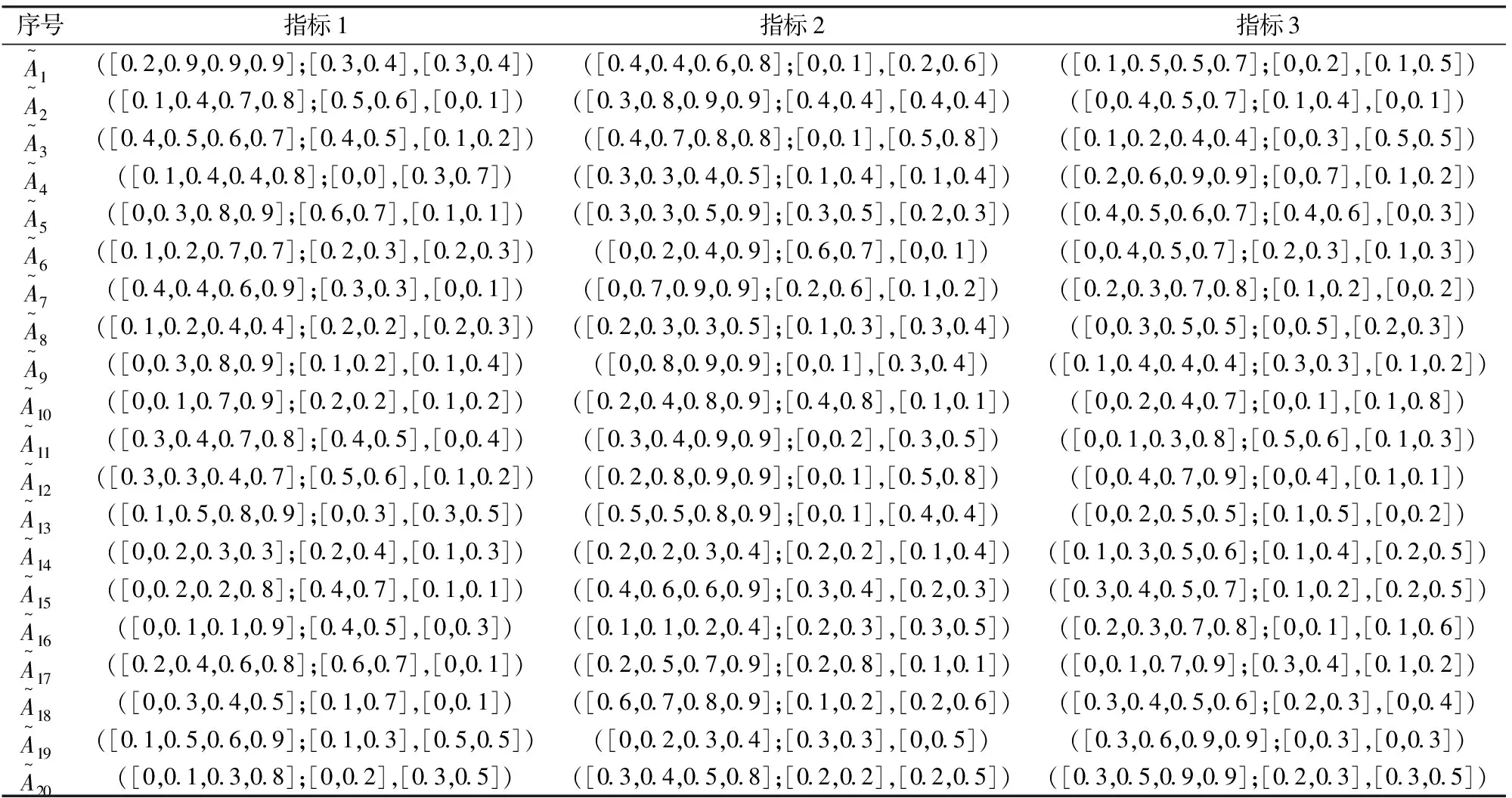
表1 方案2中群体成员的偏好矢量表

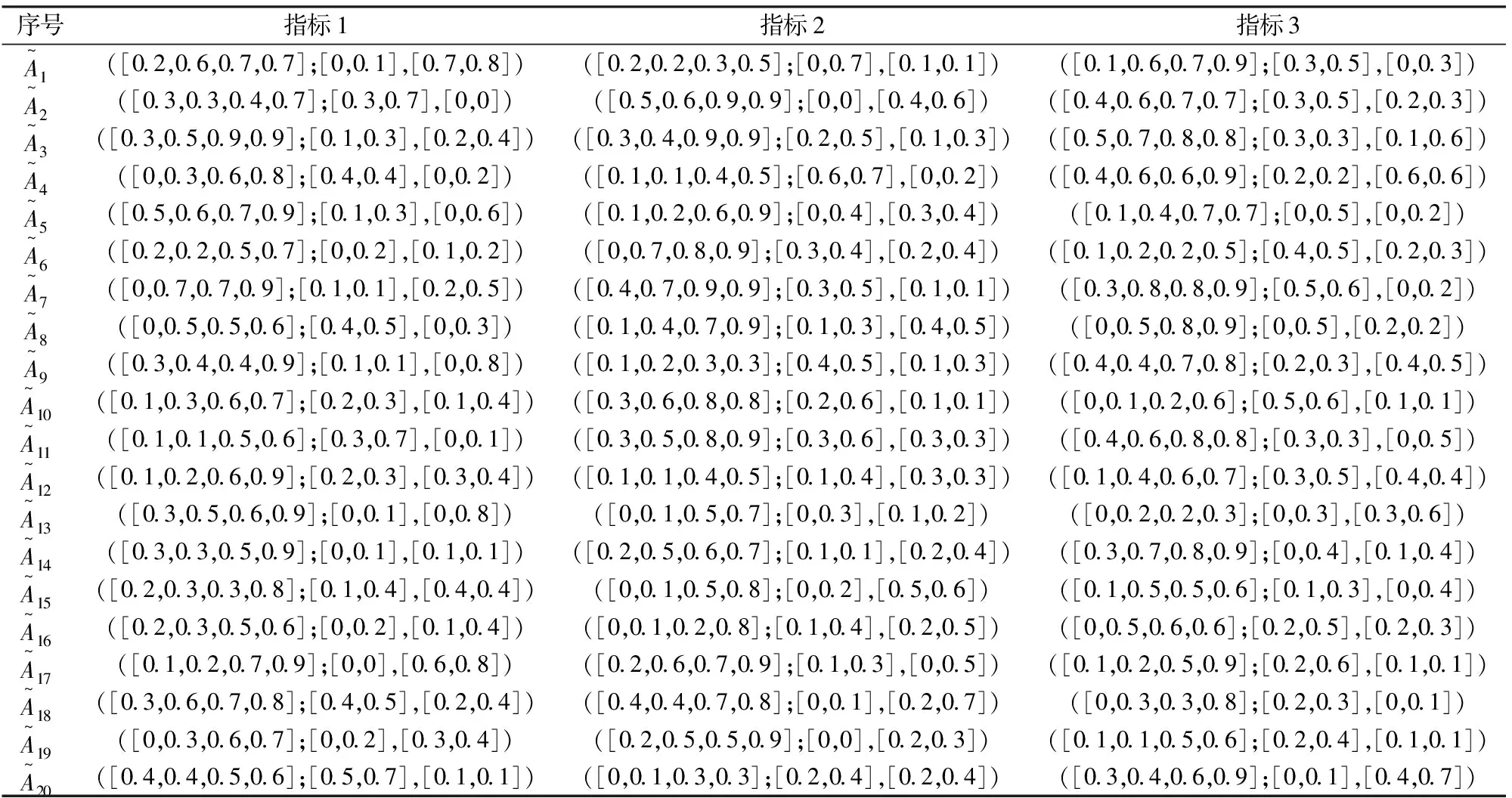
表2 方案3中群体成员的偏好矢量表

参考文献：

[1] 张云龙,刘茂.应急救援中的应急决策[J].中国公共安全(学术版),2009,(1):66-69.

[2] Jun Ye.Expected value method for intuitionistic trapezoidal fuzzy multicriteria decision-making problems[J].Expert Systems with Applications,2011,38(9):11730-11734.

[3] Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1),87-96.

[4] Chen S M, Tan J M.Hangdling multicriteria fuzzy decision-making problems based on vague set theory[J].Fuzzy Sets and Systems,1994,67(2):163-172.

[5] Liu Huawen, Wang Guojun.Multi-criteria decision-making methods based on intuitionistic fuzzy sets[J].European Journal of Operational Research,2007,179(1):220-233.

[6] Jun Ye.Improved method of multicriteria fuzzy decision-making based on vague sets[J].Computer-Aided Design,2007,39(2):164-169.

[7] 王坚强.模糊多准则决策方法研究综述[J].控制与决策,2008,23(6):601-606.

[8] 万树平.直觉模糊多属性决策方法综述[J].控制与决策,2010,25(11):1601-1606.

[9] 万树平.基于区间直觉梯形模糊数的多属性决策方法[J].控制与决策,2011,26(6):857-860.

[10] 科塞.社会冲突的功能[M].孙立平.北京：华夏出版社，1989.

[11] Boulding K.Conflict and defense[M].New York:Har per&Row,1963.

[12] Wall V D,Nolan L L.Small group conflict:A look at equity,satisfaction and styles of conflict management[J].Small Group Behavior,1987,18:188-211.

[13] Thomas K W.Conflict and negotiation processes in organizations[M]//Alto P.Handbook of Industrial and Organizational Psychology.CA:Consulting Psychologists Press,Inc.,1992.

[14] Mason R O.A dialectical approach to strategic planning[J].Management Science,1969,15(8):403-414.

[15] Cosier R A.The effects of three potential aids for making strategic decisions on Prediction accuracy[J].Organizational Behavior and Human Performance,1978,22:295-306.

[16] Schweiger D M.Experiential effects of dialectical inquiry,devil's advocacy,and consensus approaches to strategic decision making[J].Academy of Management Journal,1989,32:745-772.

[17] Guetzkow H,Gyr J.An analysis of conflict in decision-making groups[J].Human Relations,1954,7:367-381.

[18] Priem R,Price K.Process and outcome expectations for the dialectical inquiry,devil's advocacy,and consensus techniques of strategic decision making [J].Group and Organization Studies,1991,16(2):206-225.

[19] Jehn K.A qualitative analysis of conflict types and dimensions in organizational groups[J].Administrative Science Quarterly,1997,42:530-557.

[20] Jehn K.The dynamic nature of conflict:A longitudinal study of intragroup conflict and group performance[J].Academy of Management Journal,2001,44(2):238-251.

[21] 郎淳刚,席酉民,毕鹏程.群体决策过程中的冲突研究[J].预测,2005,24(5):1-8.

[22] 徐泽水.区间直觉模糊集相似性测度及其在模式识别中的应用(英文)[J].Journal of Southeast University,2007,23(1):139-143.

[23] 王坚强,张忠.基于直觉梯形模糊数的信息不完全确定的多准则决策方法[J].控制与决策,2009,24(2):226-230.

[24] Jun Ye.The decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment[J].European Journal of Operational Research,2010,205(1):202-2304.

[25] 徐选华,陈晓红.基于矢量空间的群体聚类方法研究[J].系统工程与电子技术,2005,27(6):1034-1037.

[26] 徐选华.面向特大自然灾害复杂大群体决策模型及应用[M].北京: 科学出版社，2012.

[27] 汪新凡,杨小娟.基于区间直觉梯形模糊数的群决策方法[J].湖南工业大学学报, 2012,26(3): 1-8.

[28] 徐选华,陈晓红,王红伟.一种面向效用值偏好信息的大群体决策方法[J].控制与决策, 2009,24(3):440-445(450).

[29] 徐选华,范永峰.改进的蚁群聚类算法及在多属性大群体决策中的应用[J].系统工程与电子技术, 2011,33(2):346-349.